爆炸下钢柱破坏时间及残余承载力对钢框架连续倒塌的影响*1
李国强,杨涛春,陆 勇,陈素文
(1. 同济大学 土木工程防灾国家重点实验室, 上海 200092; 2. 同济大学 土木工程学院, 上海 200092; 3. 济南大学 土木建筑学院, 山东 济南 250022; 4.爱丁堡大学 工程学院, 英国 爱丁堡 EH9 3JL)
爆炸下钢柱破坏时间及残余承载力对钢框架连续倒塌的影响*1
李国强1,2,杨涛春2,3†,陆勇4,陈素文1,2
(1. 同济大学 土木工程防灾国家重点实验室, 上海200092; 2. 同济大学 土木工程学院, 上海200092; 3. 济南大学 土木建筑学院, 山东 济南250022; 4.爱丁堡大学 工程学院, 英国 爱丁堡EH9 3JL)
建立钢框架连续倒塌单自由度(SDOF)分析模型,研究钢柱破坏时间及其残余承载力对钢框架连续倒塌的影响规律,发现钢柱破坏时间越长、残余承载力越大,结构位移响应越小.以SDOF模型响应的理论解为基础,得出在钢框架倒塌计算中是否考虑钢柱破坏时间的界限标准:当钢柱破坏时间与连续倒塌的SDOF模型周期比τ<0.2时,可忽略破坏时间的影响;当τ>3.0时,可采用静力方法计算结构响应;当0.2<τ<3.0时,需考虑破坏时间对结构连续倒塌的影响.通过对钢柱等效SDOF模型的理论分析,当其抗力模型分别为理想弹塑性和刚塑性条件时,求得柱子破坏时间的近似计算方法,并以爆炸作用后柱子变形为初始状态,结合数值方法给出钢柱残余承载力计算过程.通过对钢柱的破坏时间和残余承载力对结构倒塌影响的算例分析,表明钢柱的破坏时间(越长)和残余承载力(越大)对结构抗倒塌起有利作用,在结构抗倒塌计算时不可忽略.
钢框架; 连续倒塌; 破坏时间; 残余承载力; 单自由度模型
在爆炸作用下,构件破坏虽然持续时间很短,但并非均可简化为瞬间发生,同时,破坏构件或具有一定残余承载力.事实上破坏时间及残余承载力的存在将直接影响个别构件破坏后整体结构的响应形式.由于拆除构件法假定构件在瞬间被移除[1-3],忽略了破坏时间和残余承载力的影响,从而影响到构件破坏后整体结构响应计算结果的准确度[4-5].为提高评估钢柱损伤后钢框架抗连续性倒塌能力的准确性和可靠性,需要考虑钢柱破坏时间和残余承载力的影响.
钢柱的破坏时间是爆炸作用后柱轴力快速下降的反应时间,它主要影响结构的动力效应,破坏时间越短动力效应将越大.柱残余承载力指柱受爆炸破坏后残余的轴向承载力,在爆炸作用后,有关柱子残余承载力的研究相对较少,仅国外对混凝土柱有少量研究.Wu[6-7],Bao[8]等对爆炸作用后混凝土柱的残余承载力进行了数值研究,并试验验证了结果的合理性,同时,通过参数化分析拟合出了RC柱的残余承载力计算公式.
通过建立框架结构连续倒塌的单自由度分析模型,研究柱子破坏时间和残余承载力对结构连续倒塌的影响,给出是否考虑破坏时间的界限标准;通过对钢柱的等效单自由度模型的理论分析, 根据其抗力模型分别为理想弹塑性和刚塑性条件,给出柱子破坏时间近似计算方法,并以爆炸作用后柱子变形为初始状态,给出钢柱残余承载力计算方法.
1 钢框架连续倒塌单自由度分析模型
1.1模型的建立
为简化研究钢框架结构的连续倒塌特征和计算评估过程,同时说明拆除构件法在连续倒塌评估中的不足,可将钢框架结构的抗连续倒塌分析等效为单自由度模型,如图1所示,N为柱子移除前的轴力.柱子破坏时轴力N将衰减,其衰减模型主要有3种,如图2中(a)~(c)所示,在模型a中,采用拆除构件法将外力N瞬间移除;在模型b中,考虑爆炸作用下柱子的破坏过程,假定外力N在时间t0内线性递减至0;而在模型c中,同时考虑了柱子的破坏时间t0和残余承载力N′.

图1 结构等效单自由度模型Fig.1 Equivalent single degree of freedom model
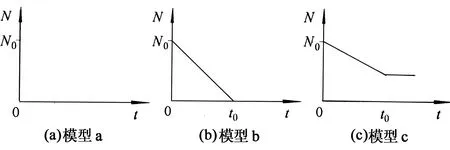
图2 轴力N的衰减模型Fig.2 Degradation model of axial force N
1.2模型的理论解
在模型a中,可通过能量平衡较简单的求得质量块最大响应表达式,但对于模型b和c而言,则其解析表达式则相对复杂.
模型a中质量块的最大位移为:

(1)
式中:xs为柱轴力N0为静力作用时对应的静位移.由式(1)可知,当突然去柱后,相当于突加荷载的SDOF结构,最大响应为其静位移的2倍.
图2(c)所示的柱子破坏模型,因同时考虑了柱子破坏时间和残余承载力的影响,为最符合实际情况的钢柱破坏模型.当钢柱以此模型破坏时,图1所示的SDOF体系位移响应为:
u=
(2)
式中:ω为模型的圆频率;定义R为体系的动力放大系数,则位移响应式(2)变为:
(3)
因此,体系的位移响应为静位移与动力放大系数的乘积,其中,动力放大系数R与体系的频率及荷载的持时有关,而静位移为:
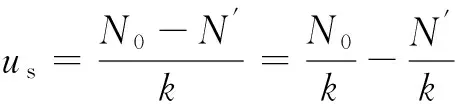
(4)
根据式(4)可知,残余承载力N′直接影响体系的静位移,残余承载力N′越小,则体系的位移响应越大,与拆除构件法相比,残余承载力的存在使体系位移减小了(N′/k)R,因此,柱子残余承载力对结构抵抗连续倒塌起着有利作用,残余承载力越大,结构抵抗倒塌的能力越强.
1.3模型的数值计算结果
在图1单自由度模型中,取质量块m为20 kg,重力加速度为10 m/s2,弹簧的线刚度为104N/m,当轴力N在图2的衰减模型a~c条件下,质量块的最大位移响应对比结果如表1所示.
分析表1数据可知,瞬间移除柱子(模型a)质量块的动力效应最大,其位移xmax最大;柱轴力N的破坏过程对位移xmax的影响与其衰减时间有关,当衰减时间较短如10 ms时(体系周期约280 ms),柱子破坏过程影响很小,可忽略不计;当柱子破坏过程较长时,其影响效果非常明显,如模型b中当轴力N衰减时间从10 ms增至200 ms的过程中位移xmax从40 mm减小至26 mm;在模型c中,其轴力N衰减时间与模型b相同,但柱子留有一定的残余承载力N′,大小为75 N,模型c中数据均小于模型b中的对应值,因此柱子残余承载力的存在大大减小了结构的最大位移.

表1 不同轴力N衰减模型下的质量块最大位移响应对比结果表Tab.1 Comparison of maximum displacement of the mass under different failure modes
1.4模型在抗连续倒塌中的应用
根据式(2)中SDOF的响应规律[9],可求得柱子破坏时间和SDOF周期对动力放大系数的影响规律,图3给出了动力放大系数随时间比t/t0的变化关系,图4给出动力放大系数最大值随破坏时间与SDOF周期比τ(τ=t0/T)的关系.
由图3知,当t0
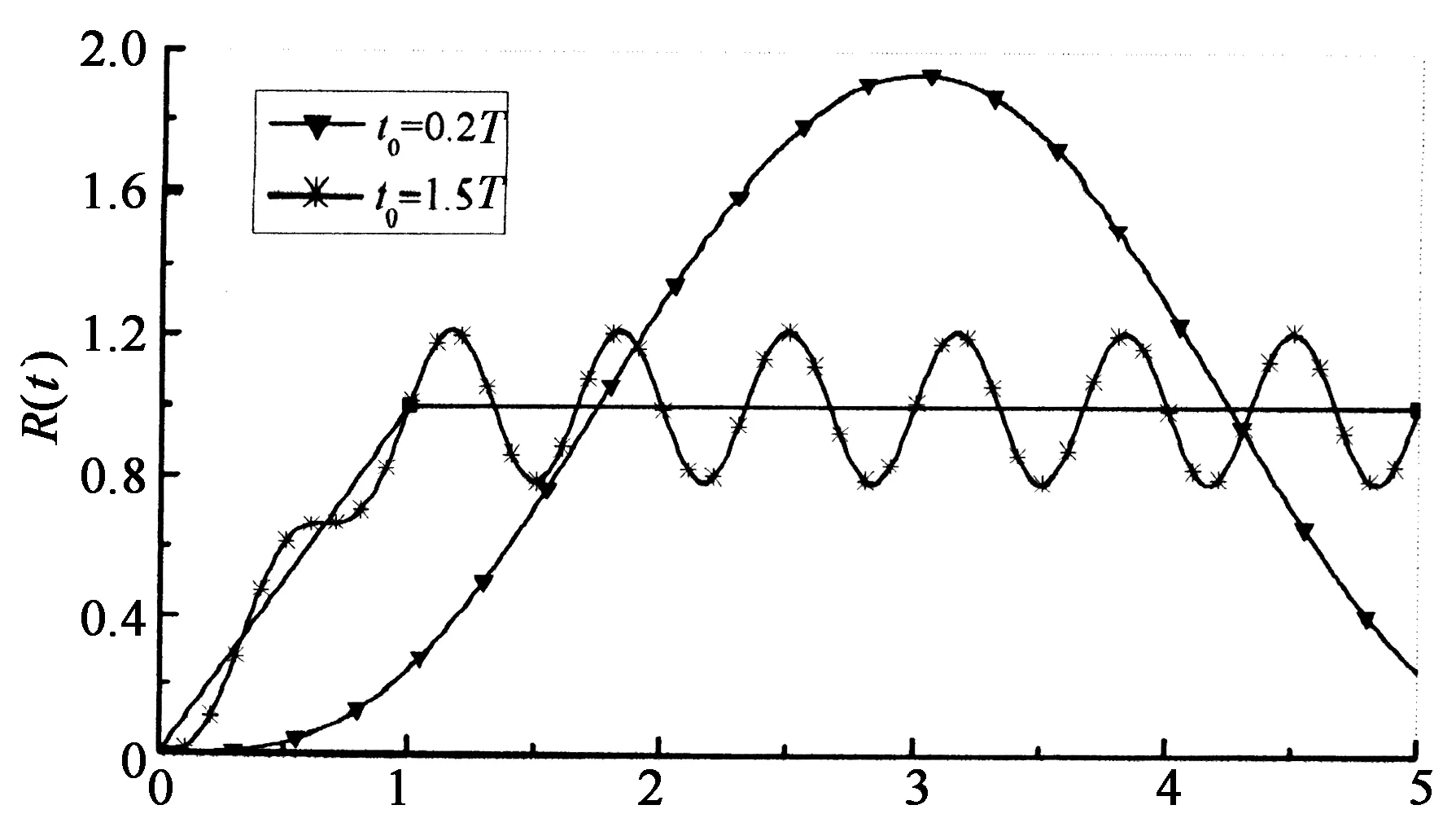
t/t0图3 动力放大系数与时间比t/t0的关系曲线Fig.3 The dynamic amplification factor versus the ratio t/t0
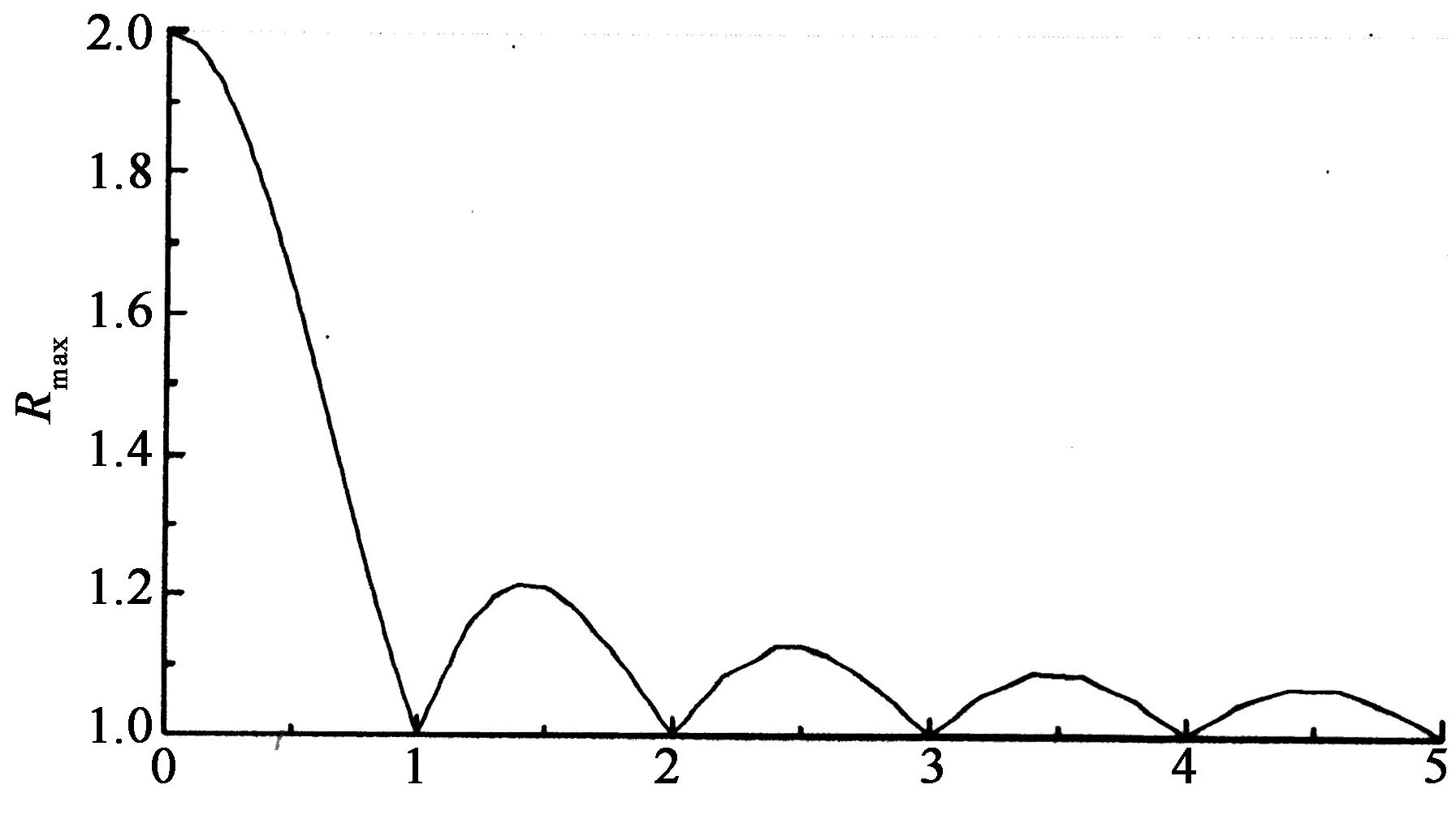
t0/T图4 动力放大系数最大值随破坏时间 与周期比t0/T的关系变化曲线Fig.4 The dynamic amplification factor versus the ratio t0/T
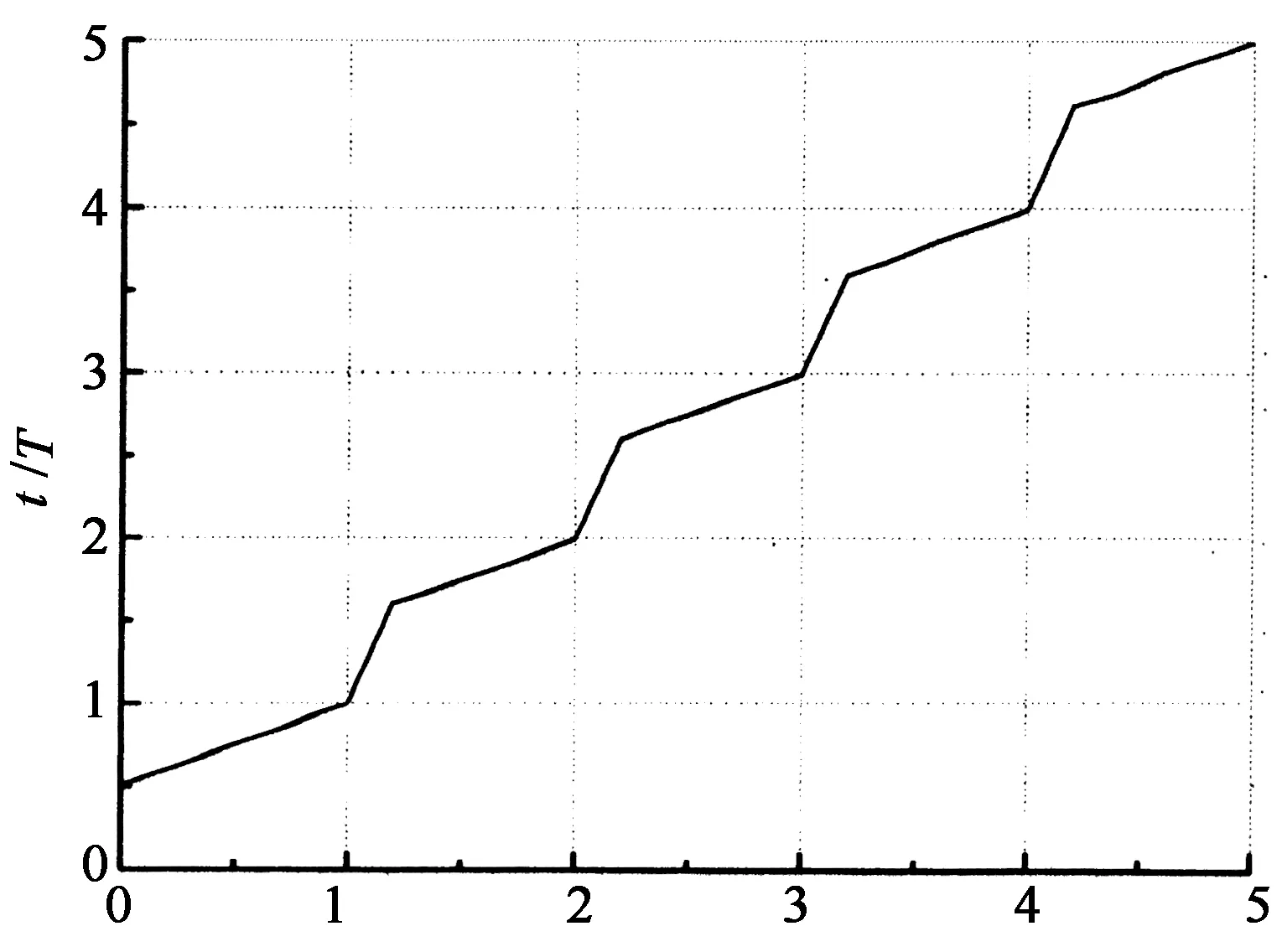
t0/T图5 最大响应发生时间随破坏时间 与周期比t0/T的关系曲线Fig.5 Occurrence time of maximum displacement versus the ratio t0/T

t0/T图6 框架连续倒塌的求解方法的选择标准Fig.6 Acceptance of methods for progressive collapse analysis of structures
2 钢框架柱破坏时间t0的确定
2.1分析模型
在爆炸作用阶段,定义柱中横向位移达到最大值的时间为钢柱的破坏时间.在爆炸作用下,当将钢框架中的受爆柱简化为两端固支时,钢柱破坏时间与钢框架柱的破坏时间几乎相等[10],即柱端约束对柱中横向位移的影响很小,可忽略不计,如图7所示[10].因此,为得到钢框架柱的破坏时间t0,可直接求解两端固支柱的破坏时间,从而简化计算过程.

图7 柱中横向位移最大值发生时间对比Fig.7 Comparison of occurrence of the maximum lateral displacement
在爆炸作用下,影响柱子破坏时间的因素有:荷载的超压峰值和持时大小(影响柱子响应模态)、钢柱截面极限塑性弯矩、钢柱的周期等,且在爆炸作用下钢柱通常具有较大的塑性变形,因此,很难给出柱子破坏时间的简单解析结果.因此,可将两端固支柱简化为单自由度模型,如图8所示,并根据SDOF模型的特性简化求解柱子的破坏时间.

图8 两端固支柱的单自由度模型Fig.8 The SDOF system of the clamped-clamped column under explosion
对于图8所示的单自由度模型,当爆炸荷载和其本身的抗力模型如图9所示时,可根据单自由度理论求得体系达到最大位移的时间,在弹性阶段和塑性阶段,SDOF模型的运动方程分别如下:
mü+ku=p(t),
(5)
mü+R=p(t).
(6)
因此,计算理想弹塑性单自由度弹簧体系就是求解式(5)和式(6)的过程.
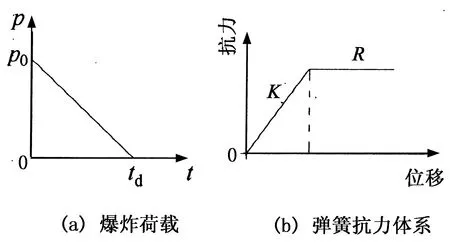
图9 单自由度模型的相关参数Fig.9 The parameters for the SDOF model
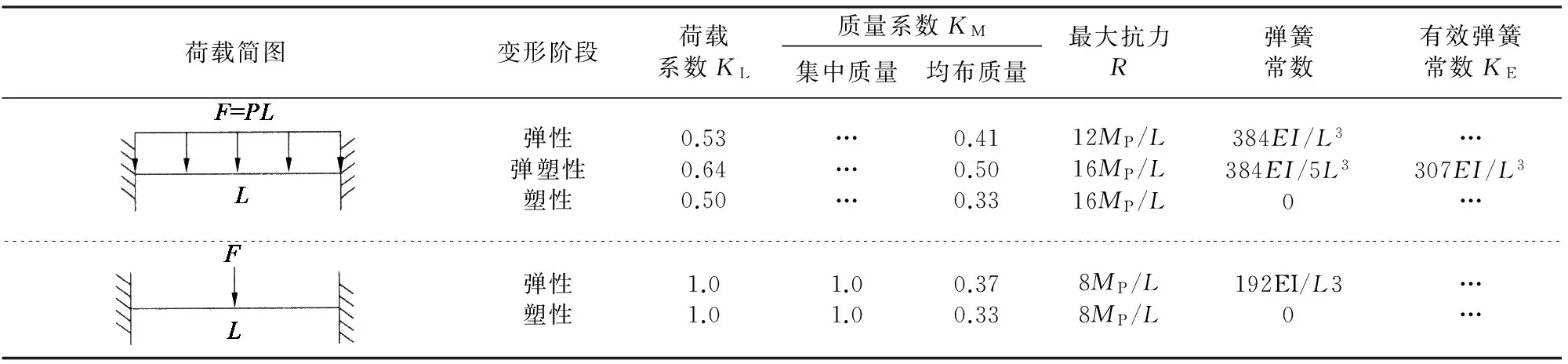
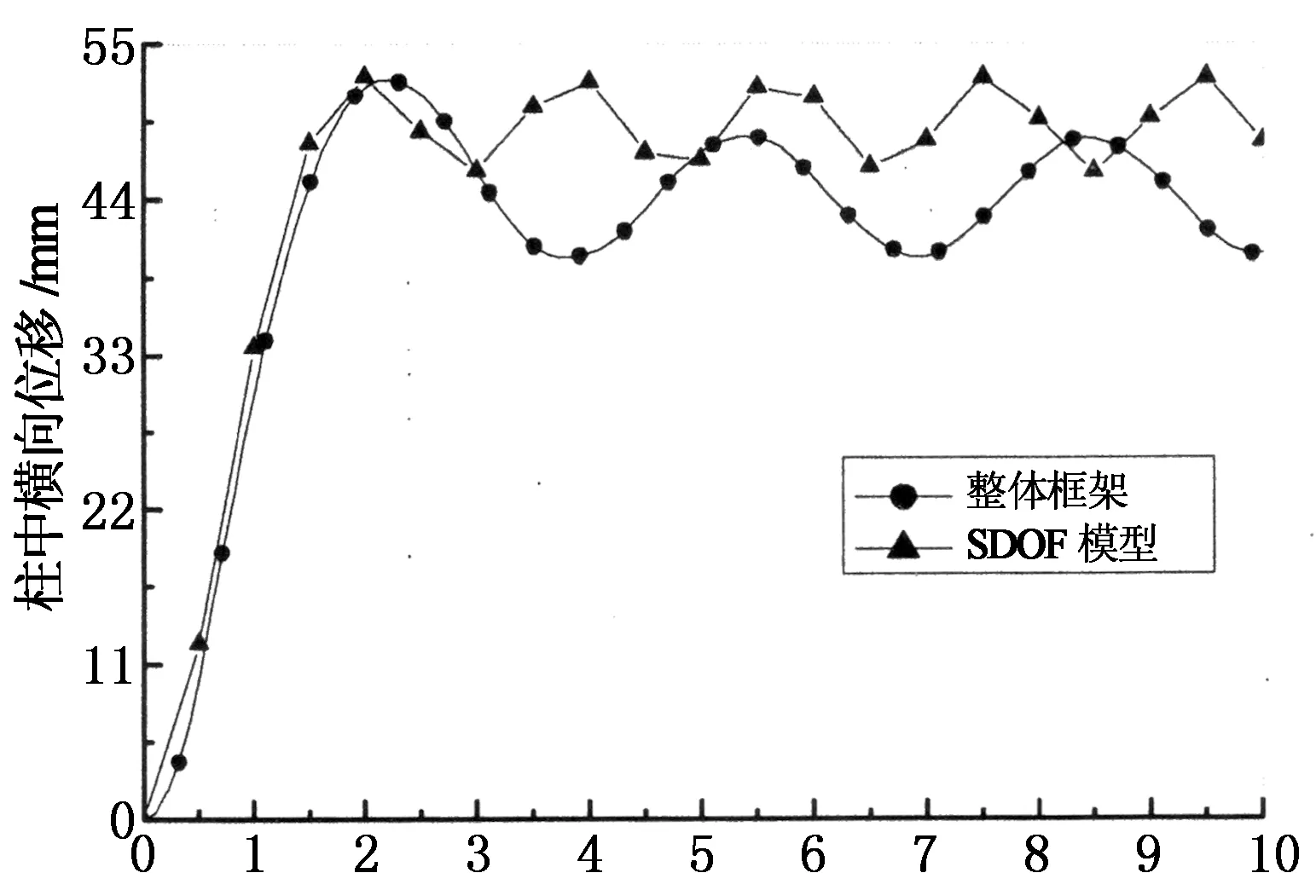
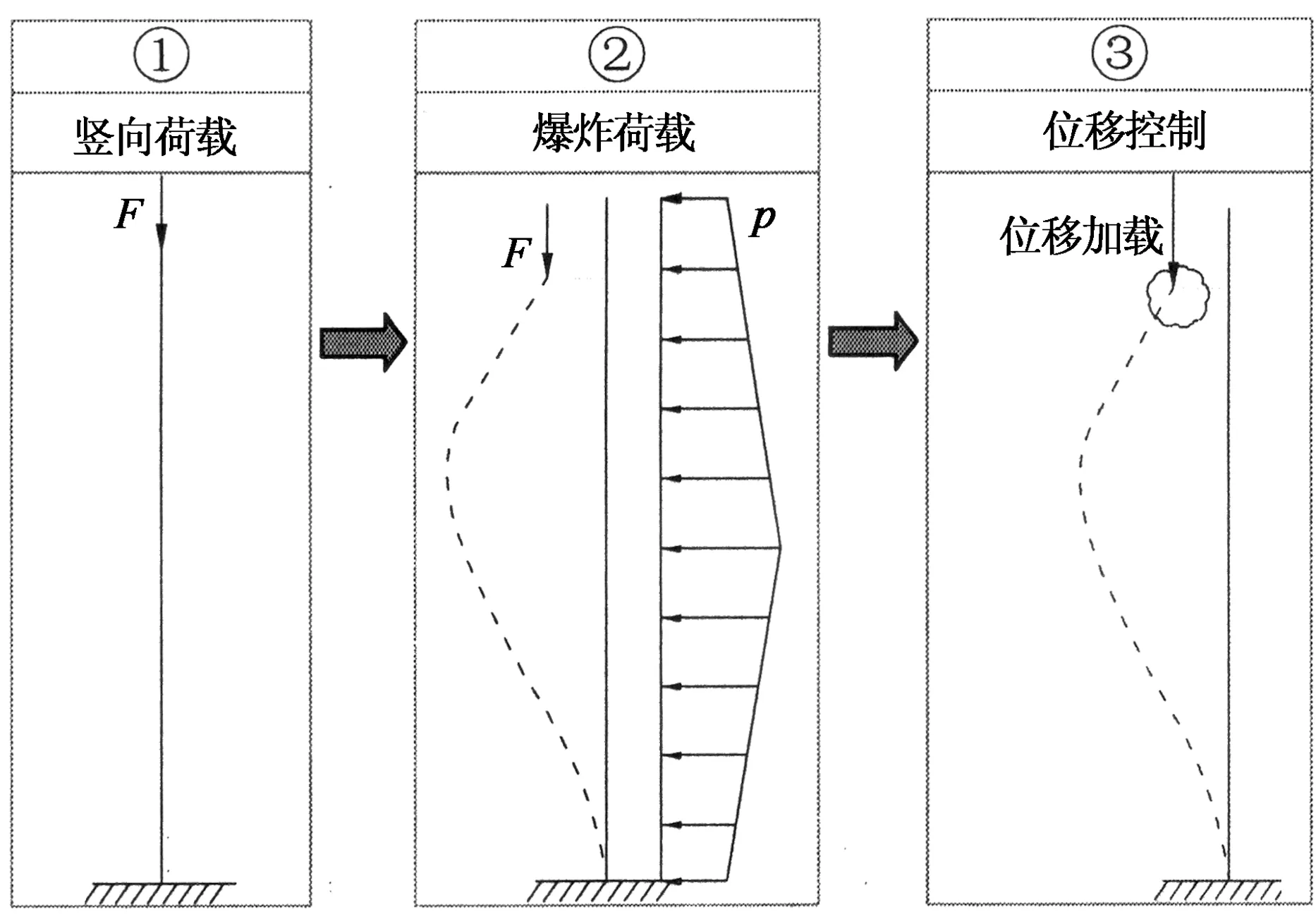
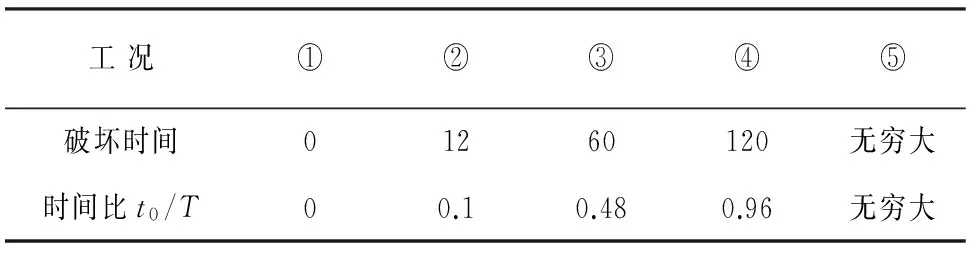
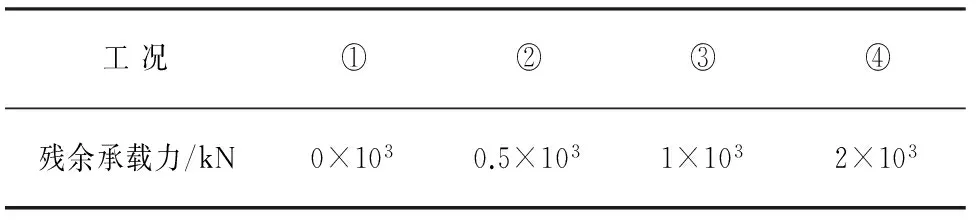
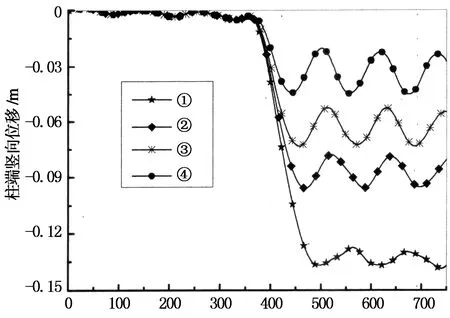
对于图8所示的单自由度模型,在弹性阶段,当t (7) 式中:ωn为SDOF模型的等效圆频率. 当td>t时,体系的位移响应式为: cosωnt(wntd-sinωntd)]. (8) 对于图8所示的单自由度模型,在塑性阶段,体系位移响应为: (9) 式中:t′为塑性阶段开始时刻.由此看来,对于理想弹塑性的单自由度抗力模型来说,由于要处理弹塑性阶段的转换过程,其动力响应求解过程仍非常复杂,需通过数值计算求解. 2.2模型参数 若知道两端固支柱的等效单自由度弹簧各参数值,利用现有的单自由度计算程序可快速计算单自由度体系达到最大值的响应时间,即柱子的破坏时间.固支柱的等效单自由度等效参数已有直接可用的研究成果,如表2所示. 表2 两端固支柱的等效单自由度模型参数[11]Tab.2 The parameters for the SDOF model of the clamped-clamped column 2.3算例 以图10的框架柱为例,根据文献[10],可求得钢柱在框架中和等效单自由度模型下的柱中横向位移对比结果,如图11所示:其中,K=2.31×106kN/m,M=202 kg,P=28.8×106kN,R=7.82×106kN.由图11知,利用等效单自由度模型可简化求解柱中横向位移和柱子破坏时间,且计算结果与实际框架中的柱子计算结果一致. 当柱子的材料和尺寸确定后,便可求得其等效SDOF模型,根据爆炸荷载的峰值和持时大小,就能确定柱子的破坏时间,以图10的框架柱为例,柱等效SDOF周期T=2.0 ms,通过调整爆炸荷载的大小,求得在不同超压峰值和持时条件下柱子的破坏时间曲线如图12,图13所示.由图可知,柱子的破坏时间随荷载持时与SDOF模型周期td/T的增大而增长,两者总体上近似呈线性关系;相同的单自由度模型条件下,由于其抗力模型具有弹性和塑性特性,因此,柱子破坏时间还与荷载的峰值有关,峰值越大,结构的塑性变形增加,柱子破坏时间增长. 图10 整体框架模型示意图Fig.10 A steel frame subjected to explosion on a ground floor column t/ms图11 SDOF和实际框架中的柱中位移对比曲线Fig.11 Comparison of the lateral displacement of the column between whole steel frame model and simplified SDOF system td/T图12 最大响应发生时间随td/T的变化关系 (P=28.8×106kN)Fig.12 Occurrence time of the maximum displacement versus td/T for P=28.8×106kN td/T图13 最大响应发生时间随td/T的变化关系 (P=18.0×106kN)Fig.13 Occurrence time of the maximum displacement versus td/T for P=18.0×106kN 2.4简化计算 虽然可通过理想弹塑性抗力模型的单自由度体系来计算柱子的最大响应时间,但其求解过程仍需要数值计算,为进一步简化计算,可将单自由度弹簧抗力模型简化为刚塑性模型[12],这样,SDOF模型的动力方程为: mü=p(t)-R. (10) 代入p(t)并积分得到式(11): (11) (12) 根据式(12)可快速简单地计算出柱子的破坏时间;以图10对应的框架柱尺寸为例,由刚塑性抗力模型和理想弹塑性抗力模型求得的柱子破坏时间对比结果如图12,图13所示.由图可知,为快速简化的估算出柱子的破坏时间,可通过刚塑性模型近似求解柱子的破坏时间. 在竖向荷载和爆炸荷载共同作用后,若钢柱进入塑性,则会保留一定的残余变形,由于此变形一般较大,钢柱残余承载力均小于其极限(稳定)承载力,因此,残余承载力值将处在柱子轴力变形曲线的下降段上,需通过有限元法或数值方法进行求解. 有限元程序如LS-DYNA可较为方便地求解钢柱承受竖向静载、爆炸荷载和残余承载力的计算全过程,其思想简单,但建模复杂,耗时较长,有限元法计算的过程如图14所示,共包括3个阶段.在第一阶段,施加竖向荷载F可得到柱子的静平衡状态;在第二阶段,以第一阶段应力状态为初始条件并继续施加爆炸荷载,求得爆炸作用下的柱子变形;在第三阶段,对爆炸作用后的变形柱施加竖向位移,得到柱子的残余承载力N′;钢柱的残余承载力主要与其初始静载、爆炸荷载和约束条件有关. 钢框架模型(图10)跨度为4.5 m,层高3 m,梁柱截面均为工字形钢,梁截面尺寸为I400 mm×200 mm×8 mm×10 mm,柱截面尺寸为I500 mm×500 mm×12 mm×15 mm,梁上竖向均布线荷载取75 kN/m. 为考察柱子破坏时间t0和残余承载力N′对结构连续倒塌的影响,在爆炸作用下,柱子轴力快速从N0降至N′,其破坏时间为t0;柱子轴力衰减模型与图2(c)相同.为便于对比分析破坏时间t0对结果的影响,假定残余承载力等于N′并恒定不变;柱子破坏时间的荷载工况取值如表3所示,钢框架结构在竖向荷载作用下,其竖向位移响应的对比结果如图15所示. 图14 LS-DYNA求解钢柱残余承载力过程Fig.14 The solution process of the residual bearing capacity of columns using LS-DYNA表3 柱子破坏时间的工况表Tab.3 Different failure time of the column ms 根据2.3节,此框架连续倒塌的单自由度模型周期T=125 ms,结合图6可知,当柱子破坏时间t0<25 ms时,可直接不考虑破坏时间的影响,取t0=0进行简化倒塌分析;当t0>375 ms时,可忽略动力效应影响,按静力方法求解;当25 ms t/ms图15 不同破坏时间下结构竖向位移对比结果Fig.15 Vertical displacement of the column versus time for different failure times 为考察残余承载力对框架连续倒塌的影响,柱子破坏时间均取t0=60 ms;柱子残余承载力的取值如表4所示,在竖向荷载为75 kN/m的条件下,结构竖向位移响应的对比结果如图16所示. 表4 柱子残余承载力N′的工况表 Fig.4 Different residual bearing capacity of the column 由图16可知,在相同破坏时间条件下,柱子的残余承载力越大,结构位移响应值越小,当柱子的残余承载力为0时(如拆除构件法),结构的位移响应值最大.因此,柱子残余承载力的存在对结构抗倒塌起着有利作用,在评估结构连续倒塌时需考虑残余承载力的影响. t/ms图16 不同残余承载力下结构竖向位移对比结果Fig.16 Vertical displacement of the column versus time for different residual bearing capacity 1)通过钢框架连续倒塌的SDOF分析模型,简明扼要的了解了柱子破坏时间和残余承载力对框架连续倒塌的影响规律:柱子破坏时间越长,残余承载力越大,对钢框架抗连续倒塌越有利. 2)当柱破坏时间与连续倒塌模型的周期比τ<0.2时,可忽略柱子破坏时间对钢框架连续倒塌的影响;当τ>3时,可忽略动力效应对钢框架连续倒塌的影响;当0.2<τ<3时,需考虑柱破坏时间对钢框架连续倒塌的有利影响. 3)可将受爆钢框架柱等效为SDOF模型,并采用刚塑性假定,简便求得柱子的破坏时间.可以爆炸作用后柱子变形为初始状态,通过弹塑性数值分析求得钢柱残余承载力. [1]JGJ 3-2001高层建筑混凝土结构技术规程[S]. 北京:中国建筑工业出版社, 2010:28-30. JGJ 3-2001Technical specification for concrete structures of high-rise building[S]. Beijing: China Architecture & Building Press, 2010:28-30. (In Chinese) [2]王开强. 空间框架结构连续倒塌评估的实用方法研究[D].上海:同济大学土木工程学院, 2009:111-121. WANG Kai-qiang. The research of practical assessment method on progressive collapse of spatial frame [D]. Shanghai: School of Civil Engineering, Tongji University, 2009:111-121. (In Chinese) [3]周健,陈素文,苏骏,等. 虹桥综合交通枢纽结构连续倒塌分析研究[J]. 建筑结构学报, 2010, 31(5): 174-180. ZHOU Jian, CHEN Su-wen, SU Jun,etal. Progressive collapse analysis of a building in Hongqiao Communication Junction[J]. Journal of Building Structures, 2010, 31(5): 174-180. (In Chinese) [4]何庆锋,刘义仁,蒋曲翀,等. 锤击作用下钢筋混凝土框架倒塌性能试验研究[J]. 湖南大学学报:自然科学版,2015,42(1): 40-46. HE Qing-feng, LIU Yi-ren, JIANG Qu-chong,etal. Experimental study of the collapse performance of RC frame under hammer load[J]. Journal of Hunan University:Naturnal Science,2015,42(1): 40-46. (In Chinese) [5]张凡榛,易伟建. 无梁楼板的抗倒塌性能试验研究及分析[J]. 湖南大学学报,自然科学版,2010,37(4): 1-5. ZHANG Fan-zhen, YI Wei-jian.Collapse experiment research and analysis of a RC flat plate [J]. Journal of Hunan University:Naturnal Sciences,2010, 37(4): 1-5.(In Chinese) [6]WU K, LI B, TSAI K. Residual axial compression capacity of localized blast-damaged RC columns[J]. International Journal of Impact Engineering,2011, 38(1): 29-40. [7]WU K B, TSAI K. The effects of explosive mass ratio on residual compressive capacity of contact blast damaged composite columns[J]. Journal of Constructional Steel Research,2011, 67(4): 602-612. [8] BAO X, LI B. Residual strength of blast damaged reinforced concrete columns[J]. International Journal of Impact Engineering, 2010, 37(3): 295 - 308. [9] CRAIG R R, KURDILA A J.结构动力学[M]. 常岭,李振邦,译.北京:人民交通出版社, 1996:84-90. [10]杨涛春. 爆炸荷载下钢柱破坏机理及其对框架连续倒塌影响研究[D].上海:同济大学土木工程学院,2013:107-118. YANG Tao-chun. The failure mechanism of steel column under blast loading and its effect on progressive collapse of steel frame [D]. Shanghai: School of Civil Engineering, Tongji University, 2013:107-118. (In Chinese) [11]CRAWFORD R E,HIGGINS C J,BULTMANN E H. The air F force manual for design and analysis of hardened structures[M].New Mexico: Civil Nuclear System Corporation, 1980:368-372. [12]钱七虎,王明洋. 高等防护结构计算理论[M]. 南京:江苏科学技术出版社, 2009:80-81. QIAN Qi-hu,WANG Ming-yang.Calculation theory for advanced protective structures[M].Nanjing:Jiangsu Science & Technology Press,2009:80-81. (In Chinese) Effects of Steel Column’s Failure Time and Residual Bearing Capacity on Progressive Collapse of Steel Frames Subjected to Blast LI Guo-qiang1,2, YANG Tao-chun2,3†, LU Yong4, CHEN Su-wen1,2 (1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji Univ,Shanghai200092, China; 2. School of Civil Engineering, Tongji Univ, Shanghai200092, China; 3. School of Civil Engineering and Architecture, Univ of Jinan, Jinan,Shandong250022, China; 4. School of Engineering, The Univ of Edinburgh, EdinburghEH9 3JL, UK) The influence law of failure time and residual bearing capacity of the steel columns on progressive collapse of steel frames was studied by using a single degree of freedom (SDOF) model. The displacement of the steel frames decreases as the failure time and residual bearing capacity of the steel columns increase. On the basis of the theoretical solution of the SDOF model, boundary condition of the model was determined to consider the failure time effect.τwas defined as the ratio of the failure time to natural period of the SDOF model. Forτ<0.2, the failure time can be ignored. Forτ>3.0, a static method can be used to estimate the structure behavior. However, for 0.2<τ<3.0, the failure time should be considered in the progressive collapse analysis. When the resistance model is ideal elastic-plastic and rigid-plastic, the equivalent SDOF model of the steel columns can be theoretically analyzed to determine the calculation method of the failure time. Considering the deformation of the steel columns after explosion as the initial state, the calculation process for the residual bearing capacity of the steel columns is gained by combining with numerical calculations. The results show that the failure time and residual bearing capacity significantly influence on the progressive collapse of the steel frames, and those effects should be considered in the progressive collapse analysis. steel frame; progressive collapse; failure time; residual bearing capabicity; single degree of freedom model 2015-03-10 国家自然科学基金国际合作与交流项目 (51120185001),Projects of International Cooperation and Exchanges NSFC(51120185001) 李国强(1963-),男,湖南株洲人,同济大学教授,博士†通讯联系人,E-mail:yangtaochun@126.com 1674-2974(2016)05-0001-08 TU312.3 A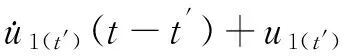






3 钢柱残余承载力的计算
4 影响分析

5 结 论

