储油罐的变位识别与罐容表标定
肖同,王卓,陈钗,杨艳梅
(华北理工大学 理学院,河北 唐山 063000)
储油罐的变位识别与罐容表标定
肖同,王卓,陈钗,杨艳梅
(华北理工大学 理学院,河北 唐山 063000)
罐体变位识别;罐容表的标定;积分;差值
运用积分思想,建立了油罐体积与油位高度的数学模型。在无变位情况下,根据油罐体积与油位高度的关系式和实际采集的数据结果,在同一坐标系下作出无变位时储油量与油位高度的曲线图,求出储油量与油位高度的函数关系式,建立了罐内储油量与油位高度及变位参数之间的关系模型。确立了油位高度和变位参数之间的关系式,并求出左右球冠和中间圆柱体的储油量。研究结果表明:储油罐罐容表标定并不是一成不变的,应根据实际生活需要收集数据对有关部门制定的罐容表标准进行修正,重新标定罐容表。
加油站有若干个储存在地下的储油罐,并有与之配套的“油位计量管理系统”。储油罐用过一段时间后,地基可能发生变化,罐体发生横向倾斜和纵向倾斜从而导致罐容表的标定值与实际值不符。所以,有必要定期重新标定罐容表。要识别储油罐的变位和罐容表的标定,针对该问题,运用微积分基本原理,建立了储油罐变位前与变位后储油量与油位高度关系的数学模型,进而计算出实际油量表,并确定了储油罐的变位参数,依据实际生产中采集到的数据对模型进行验证,研究结果表明所建立的模型符合采集数据,具有较高的精确度和参考价值。
1 罐体无变位时的求解
设椭圆型储油罐无变位时储油量体积为V1,纵向变位后储油量体积为V2,S(y)为在y点时截面的面积,H1为罐体内油位高度,H2为无变位时油位高度,L为椭圆储油罐体的长度,l1为油位探测装置到油罐两底面中较近一面的距离。
当储油罐体无变位时横截面积与油位高度的函数关系式满足:
(1)
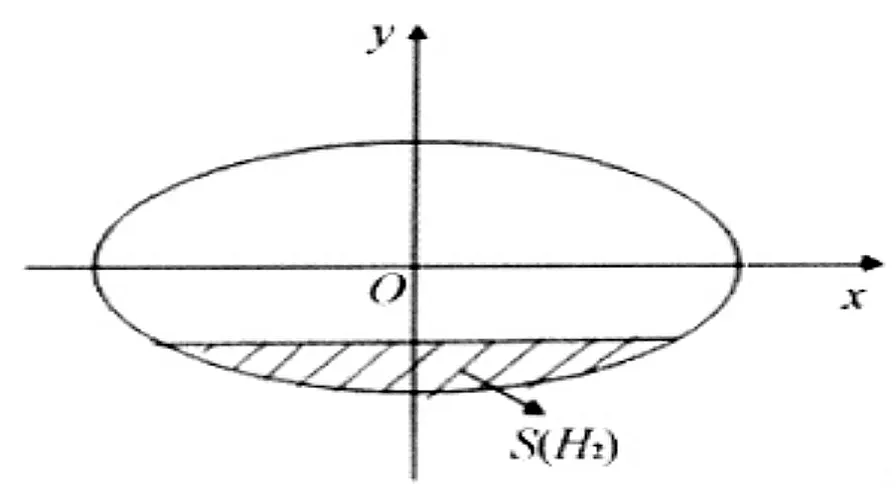
图1 椭圆截面示意图
其中S(H2)为椭圆截面面积,且
(2)
运用定积分求体积的公式结合柱体体积的计算方法[1],得到储油罐无变位时储油量V1与罐内油位高度H2的关系:
(3)
当储油罐体纵向变位时,罐体内任意一点z处的高度h(z)满足:
h(z)=H1+l1tana-ztana
(4)
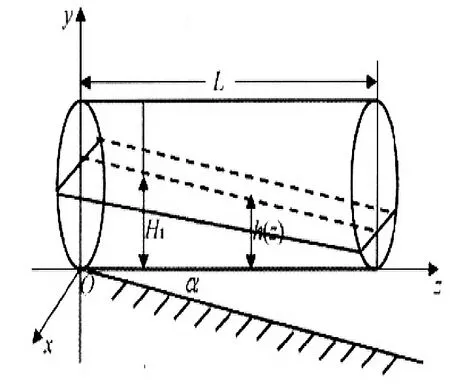
图2 椭圆柱体截面示意图
联立以上各式解得任意椭圆截面横截面积为:
(5)
其中,
(6)
根据立体体积的计算公式有:
(1)无变位情况时
对上式化简可以得到无变位时油罐体积与油位高度之间的关系为:
(7)
将该结果与实际测量数据在以同一高度为横坐标,体积为纵坐标的坐标系中作图,如图3所示。
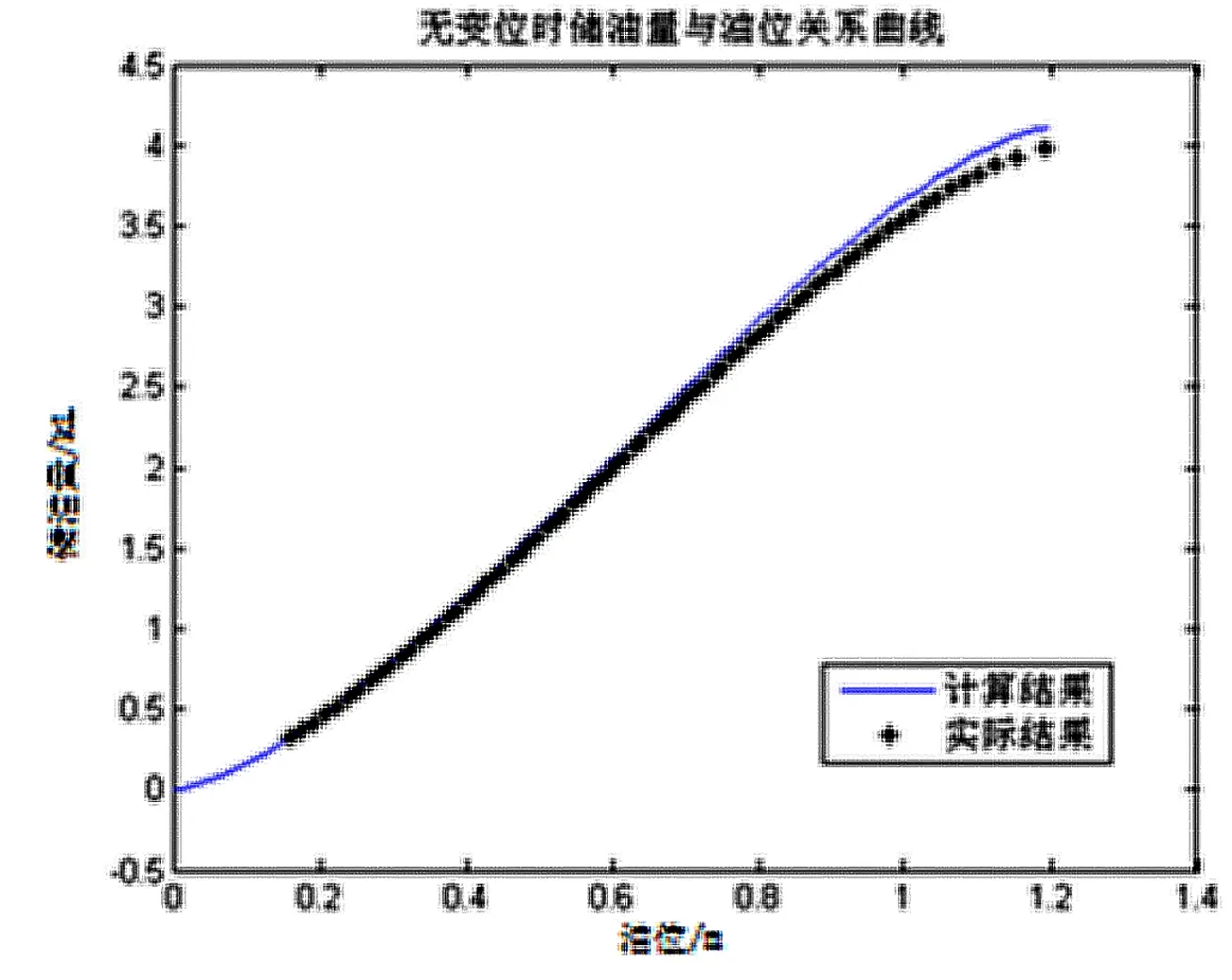
图3 无变位时计算结果与实际结果对比图
(2)发生α=4.1o纵向偏移的情况时
以椭圆油罐的罐底为原点,X轴,Z轴平行于罐底,Y轴平行于油罐侧壁的方向建立空间直角坐标系,如图所示。
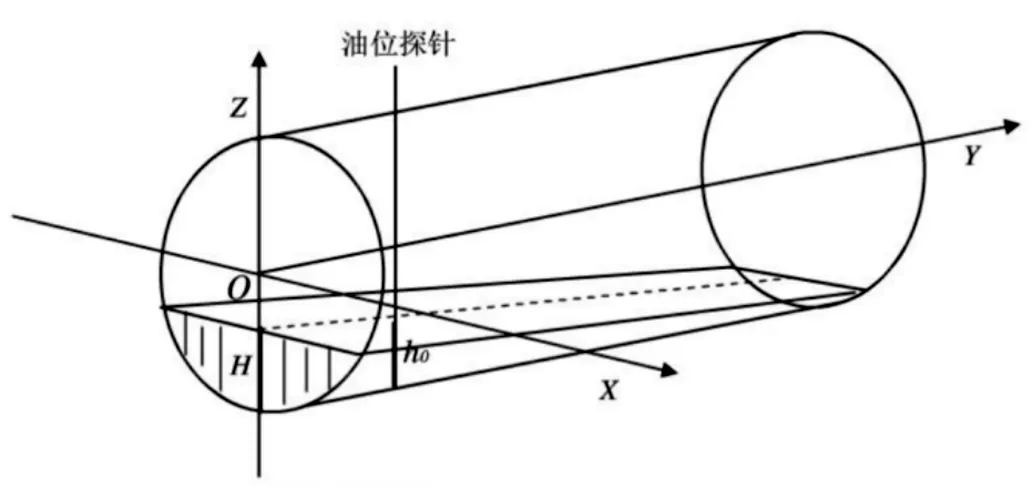
图4 纵向变位情况下建立的空间直角坐标系
由图4可知,距油罐底面为y处的油面高度的函数关系式为:
(8)
可以得到H=h0+(0.4-y)tanαy∈[0,2.45]
假设油浮子到达最高处便不再加油,罐容表示数为0时不再出油,则h0∈[0,1.2];z∈[0.4tanα-0.6,0.6];
根据H与y的关系式,考虑y、z的范围,把储油罐的储油情况分为以下3种[2]:
(1)H(2.45)⦤0,即0⦤h0⦤2.05tanα,此时油面与侧面的交点y轴方向上的坐标为h0tanα+0.4。
则此时储油罐里的油量为:
(9)
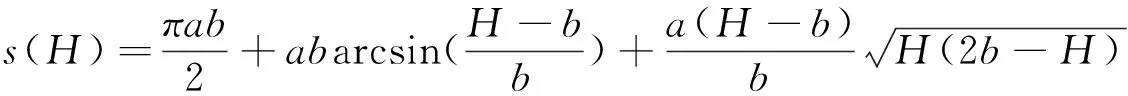
(10)
H=h0+(0.4-y)tanα
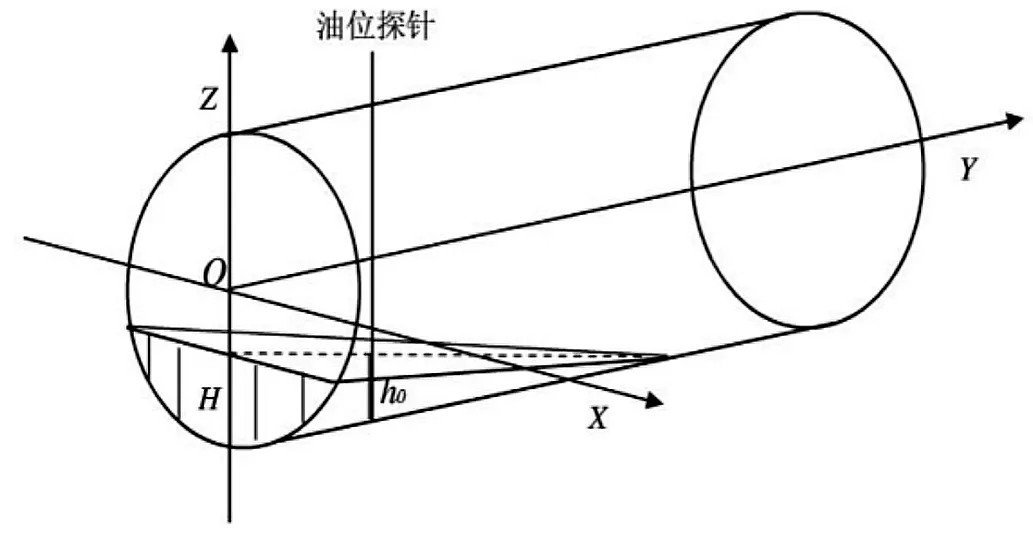
图5 第1种情况
把所求H代入S(H)的表达式得:
(11)
其中H=h0+0.4tanα,α=4.1o,a=0.89,b=0.6。
(2)H(2.45)≥0,H(0)⦤1.2,得到2.05tanα⦤h0⦤1.2-0.4tanα 两端罐底都接触油面如图6所示。
此时储油罐的油量体积为[3]:
(12)
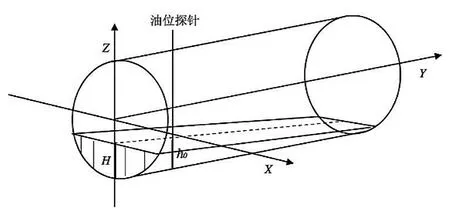
图6 第2种情况
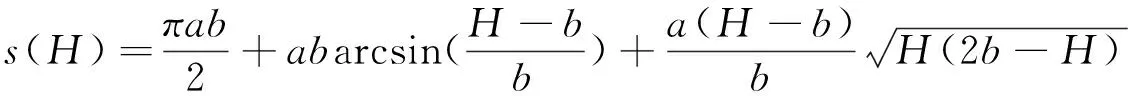
(13)
H=h0+(0.4-y)tanα
代入求得V2=V2(H1)-V2(H2)
(14)
其中H1=h+0.4tanα,H2=h0-2.05tanα,α=4.1o,a=0.89,b=0.6。
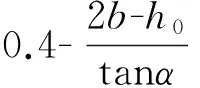
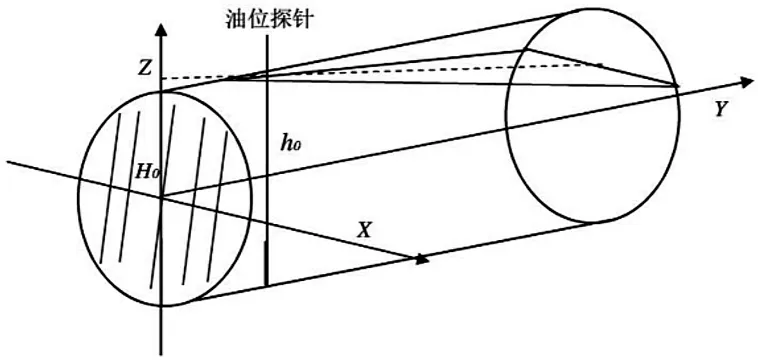
图7 第3种情况
此时油面上方的体积为:
(15)
整体油桶的体积为:V0=πab
其中
(16)
(17)
其中H1=2b,H2=h-2.05tanα,α=4.1o,a=0.89,b=0.6。
将上述3种情况得到的方程式分区间画在同一坐标系中,并与实际测量的数据做对比,如图8所示。
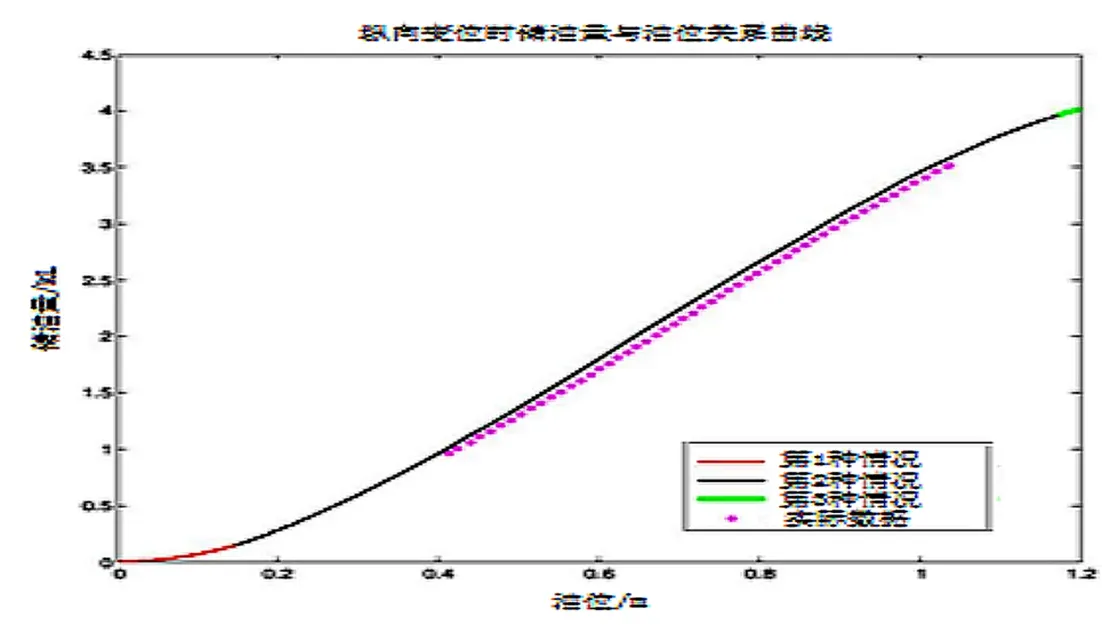
图8 变位后储油量与油位高度关系
从图8可以看出,计算得到的公式基本符合实际检测数据。通过代入数据,误差保持在3%以内。因此,在标定罐容表时,以得到的公式为基础,代入数据计算。
从0~1.20 m,每间隔0.01 m取一数值代入公式,得到如下罐容表的标定值:
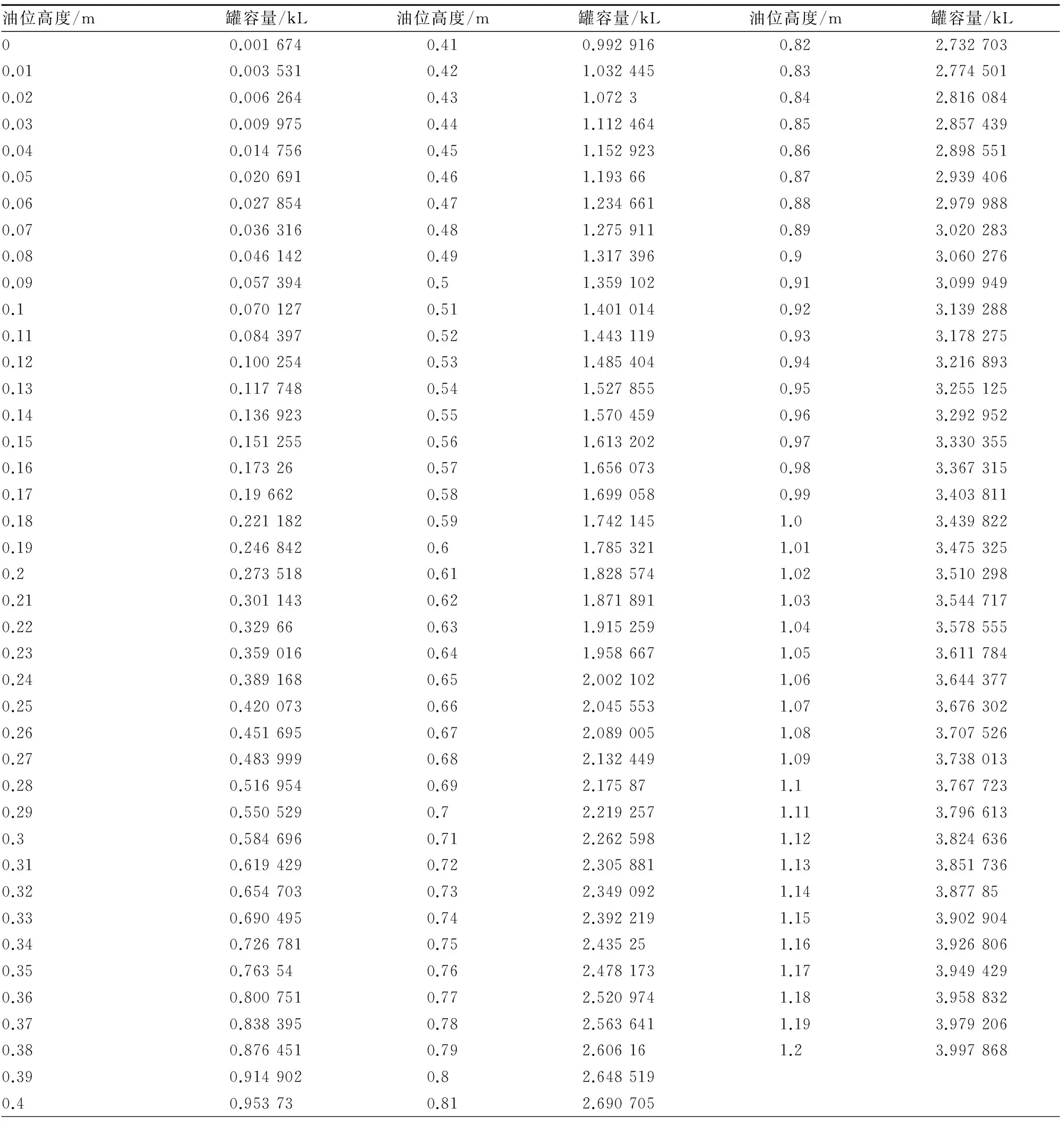
表1 纵向变位后的罐容表标定值
2 罐体纵向变位后的求解
将储油罐分成3段来考虑,两端为球缺,中间为圆柱体[4]。中间部分釆用类似于第1种情况的积分方法求解。对于两端的球冠体,若直接积分,结果将十分复杂,为方便计算,同时使误差尽量小,该项研究把球冠内油液面看成与Y轴平行。
对于纵向与横向已变化好的静态储油罐来说,以中间圆柱体一侧底面圆心为原点,平行于罐体的轴为Y轴,平行于油面的轴为X轴建立空间直角坐标系[5]。
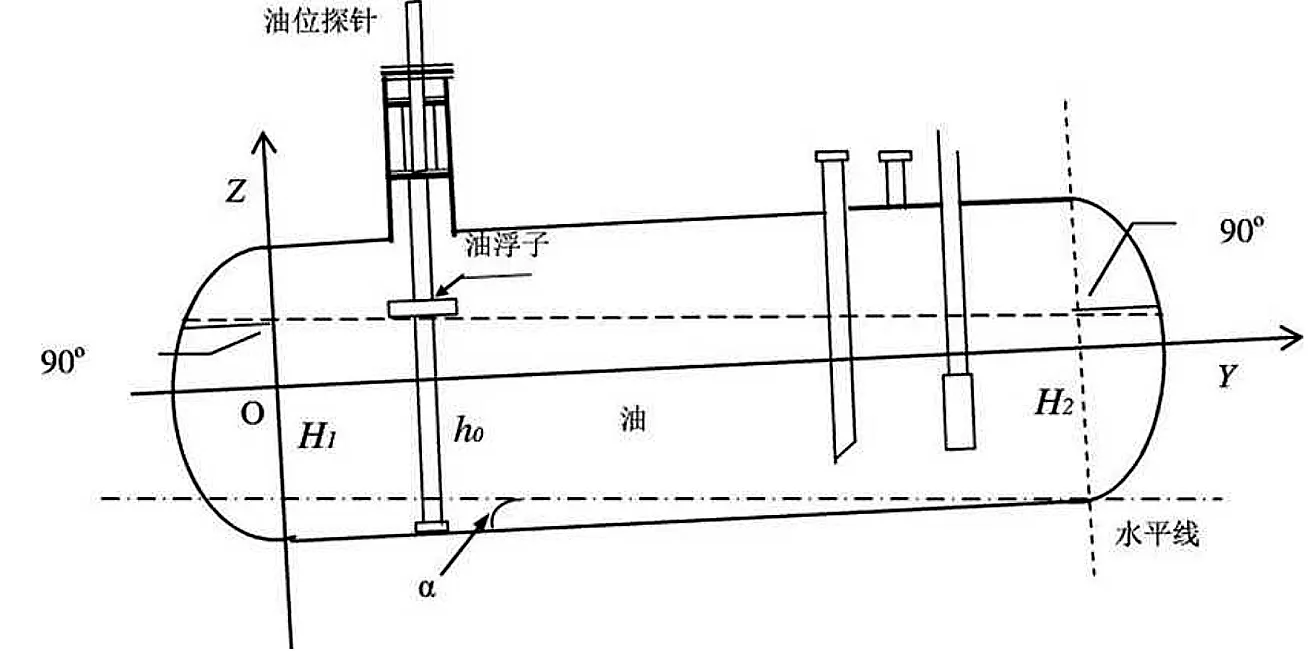
图9 储油罐纵向变位示意图
根据图9可以得到以下关系式(18):
(18)
用垂直于Y轴的平面去截储油罐,得到图10所示的储油罐的横向变位截面示意图,图中2个油液面是指将横向变位前后的截面图画在一个图中,并使油位探针方向相同,以方便计算[6],此时前后液面形成夹角β。
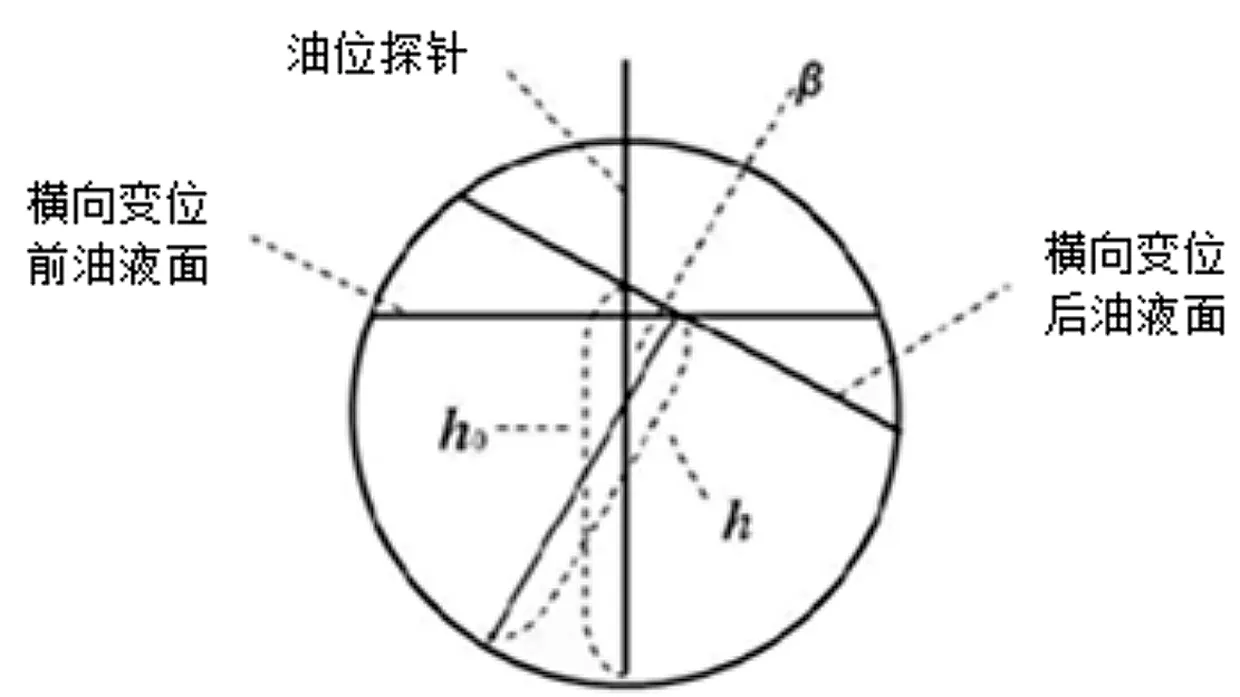
图10 横向变位截面示意图
h0为测量值,h为实际油位高度,根据图像可以得到如下关系式(19):
h=(h0-1.5)cosβ+1.5
(19)
综合上面几个式子,可以得到如下关系式(20):
(20)
球冠体内储油量的计算:
根据已知数据可解得球冠所在球的半径为1.625 m,球冠球心的截面图如下,以圆心为原点,平行于空间坐标系Y轴的轴为X轴,建立新的平面直角坐标系,阴影部分为:
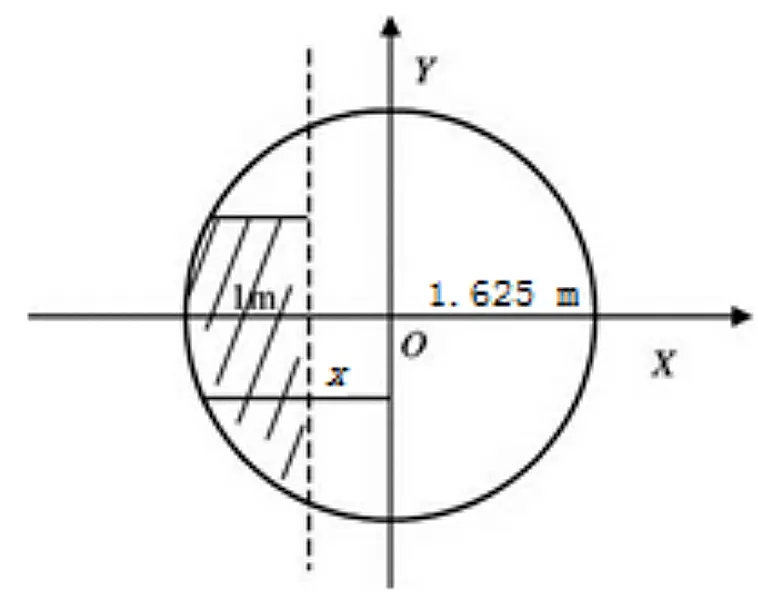
图11 球冠体还原为球后的截面图
该圆的方程为: x2+y2=1.6252
X表示圆上一点到Y轴的距离,所以:
以平行于空间直角坐标系Y轴的平面去截取球冠,得到如下截面:
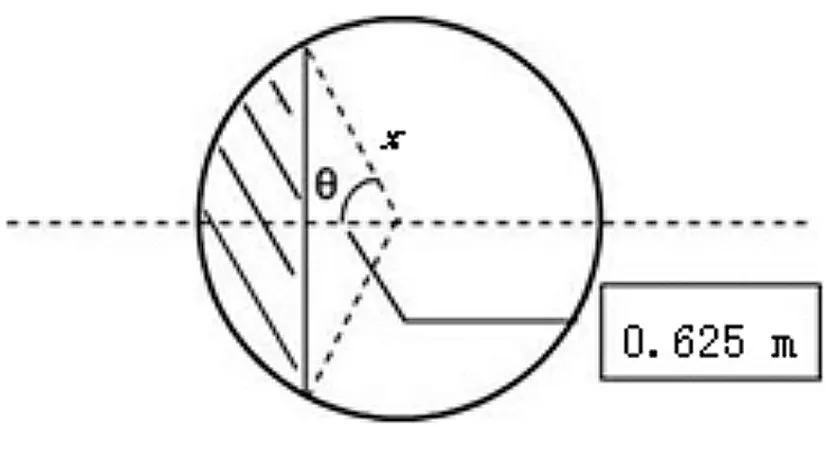
图12 球冠体截面图
可知:
所以球罐内油料截面面积为:
当球冠内油位高度为H时,球冠内储油量为:
(21)
在计算两端球冠内储油量时,分别用H1,H2代替H即可求出结果。
中间圆柱体内储油量计算[7]
中间圆柱体内储油量计算的方法与第1种情况类似,用垂直于Y轴的平面去截取油罐得到如图13所示。
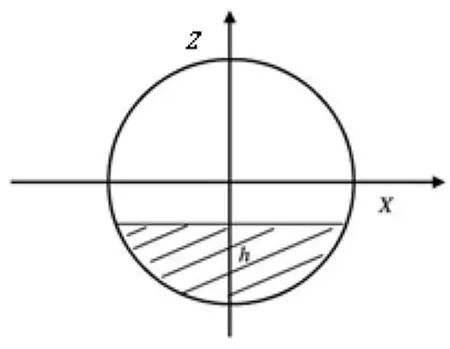
图13 截面示意图
截面圆的方程为:x2+z2=1.52
又由: h=-ytanα+H1
有3种情况,分别讨论:
当2tanα (22) 当8tanα (23) 当3-8tanα V03=V0-V01 (24) 其中V0为圆柱体的总体积。 参数α,β的确定: 由于第2种情况的可能性最大,数据最多,所以在求解参数α与β时,利用油高值在中间部分的值进行计算。由于显示的油量容积是利用没有变位情况下的公式计算得到的,不是真实值,故不能加以利用。出油量与显示油高的对应数据,用差值计算,即利用累计出油量与油高的变化值的对应关系求解α,β。. 取流水号分别为323、337、351的3组数据, 令:h1=1 696.61h2=1 609.06h3=1 516.81 得到如下方程组: 用Matlab求解该方程组[8],得到一组解α=1.6o,β=0o 由此得到了变位后储油量与高度的关系式,间隔10 cm取值代入得到如下容表标定值: 表2 变为后实际储油罐罐容表标定值 得到关系曲线, 图14 变位后储油量与油位高度关系图 (1)采用积分思想建立了储油罐在无变位及纵向变位2种情况下储油量与油位高度之间关系的数学模型,结合实验和实际测量的数据,分析讨论3种情况椭圆形油罐变位问题,对变位时罐容表进行了标定。 (2)通过数据分析可以看出,求解的结果误差较小,稳定性较高,适用范围较广。 [1]管冀年,赵海.卧式储油罐罐内油品体积标定的实用方法[J]. 计量与测试技术,2004,28(6):124-127. [2]李致荣.椭圆柱体卧式油罐容积的计算[J].数学的实践与认识,1977,4(1):17-26. [3]田铁军.倾斜卧式罐椭圆直筒部分容积的近似计算[J].现代测量与实验室管理,2004, 1005-3387(1):26-27. [4]冯杰,黄力伟,王勤,等.数学建模原理与案例[M].北京:科学出版社,2007. [5]高恩强,丰培云.卧式倾斜安装圆柱体油罐不同液面高度时储油量的计算[J]. 世界金属导报,1998,20(1):26-28. [6]冯波,温淑慧,齐广学.基于多参数传输油罐液位测量方法的研究[J]. 传感技术学报,2002,6(2):11-14. [7]蒋心亚,宗光.各种形状封头的圆筒形卧式容器在不同液面高度时液体体积计算的统一表达式[J].化学设备与管道,2003,39(5):30-34. [8]刘卫国.MATLAB程序设计与应用(第二版)[M].北京:高等教育出版社,2006. Displacement Identification of Oil Storage Tank and Calibration of Tank Capacity Gauge XIAO Tong, WANG Zhuo, CHEN Chai, YANG Yan-mei (College of Science, North China University of Science and Technology, Tangshan Hebei 063000,China) displacement identification of tank;calibration of tank capacity gauge;integral;difference value The mathematical model of the oil tank’s volume and the oil level height are established by integral thought. Based on the real data and relation between the oil tank’s volume and the height of oil level, the curve of oil reserves and oil level height without displacement is drawn under the same coordinate system. Then the relational model of the height of oil level and the deflection parameter is established, and the oil reserves about the ball and the cylinder in the middle is determined. The results show that the tank capacity table calibration of the oil tanks is not invariable. The standards for tank capacity table made by some authorities concerned should be amended and rescaled according to our actual need. 2095-2716(2016)03-0076-10 TH715.3 A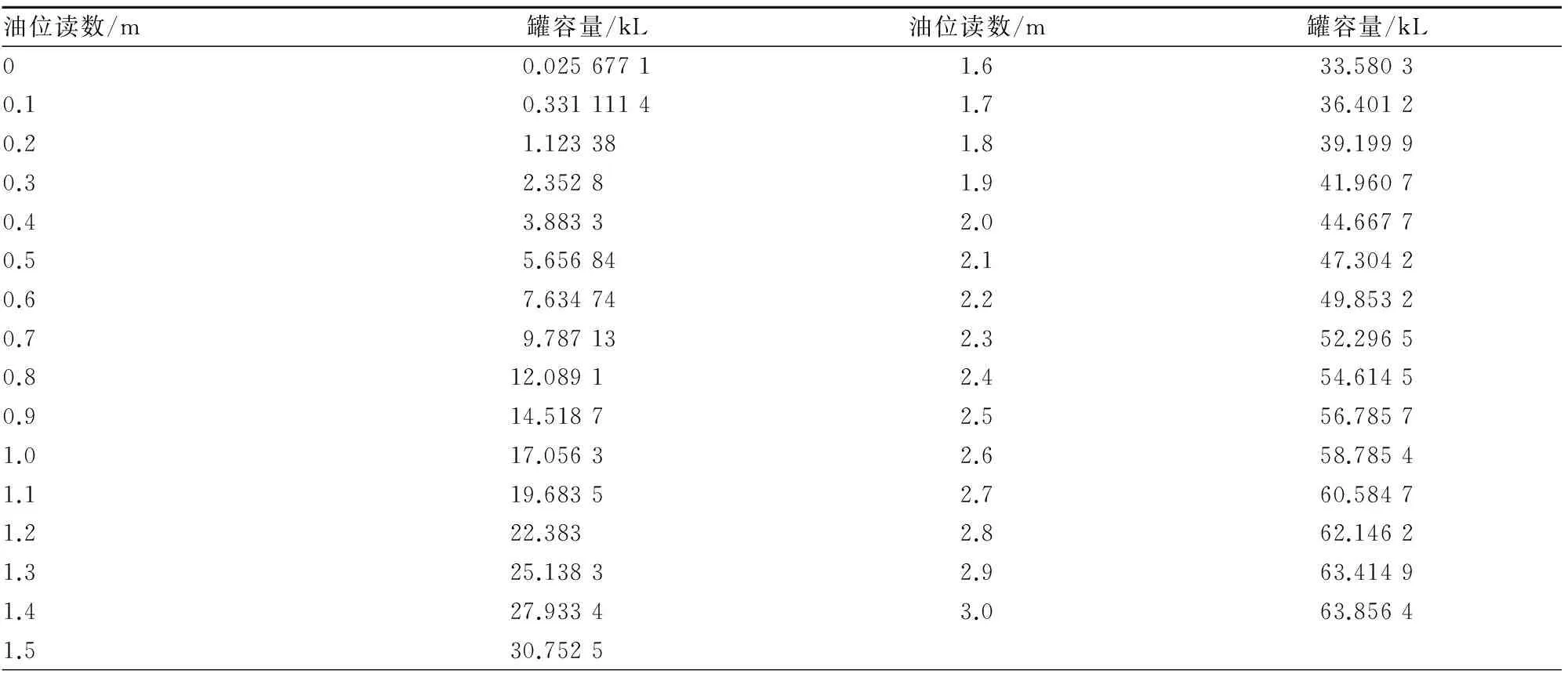
3 结论

