货叉扁钢精轧过程金属流动规律的数值模拟
杜金龙,张贵杰,王立亚
(1. 华北理工大学 冶金与能源学院,河北 唐山 063009 ;2. 华北理工大学 理学院,河北 唐山 063009)
货叉扁钢精轧过程金属流动规律的数值模拟
杜金龙1,张贵杰1,王立亚2
(1. 华北理工大学 冶金与能源学院,河北 唐山 063009 ;2. 华北理工大学 理学院,河北 唐山 063009)
扁钢;精轧;金属流动规律;宽展系数;数值模拟
为了更好地控制货叉扁钢的尺寸精度,省去后续加工,根据某钢厂生产货叉扁钢的轧制工艺,建立了货叉扁钢的热连轧模型,利用有限元软件DEFORM对扁钢精轧过程进行数值模拟。根据模拟结果分析了不同温度和摩擦系数对金属流动规律的影响,并通过曲线拟合的方式,得到了货叉扁钢宽展系数的数学模型,为制定合理的工艺参数,提高产品的尺寸精度提供可靠的理论依据。
用轧制方法生产的钢材,具有多品种、高生产率、易于实现机械自动化、生产连续性强等特点。随着市场竞争日趋激烈,以及经济的快速发展和科学水平的迅猛提高,对钢材的要求已经向着质量高、成本低、品种多方向转化。轧钢生产技术的研究和开发的主导思想也向着利于市场竞争的方向发展。因此,钢铁研究和生产部门所要面临的重要课题就是如何扩大产品规格、优化生产工艺和提高产品质量[1,2]。
1 扁钢的高精度轧制
扁钢高精度轧制能有效地提高产品的尺寸精度,提升产品的合格率,为企业创造更高效益,在工业生产中有着非常广泛的应用空间[3,4]。货叉扁钢在精轧过程中的宽展系数是影响产品尺寸精度的重要参数,而宽展系数又受到温度、摩擦系数、压下率、轧制速度、轧辊辊径、孔型尺寸和形状等多种工艺参数的影响[5]。因此,如果能掌握这些因素对轧件变形区宽展方向金属流动规律和宽展系数的影响,将对提高产品精度和优化生产工艺参数起到至关重要的作用[6]。
依据现场生产的实际情况,利用DEFORM有限元数值模拟软件,建立了扁钢轧制模型,设置了不同的初始条件和边界条件,通过正交法对扁钢高精度轧制过程进行了模拟计算。根据模拟结果分析不同工艺参数对金属流动规律和宽展系数的影响,为现场生产提供理论支持。
2 计算模型的确定
2.1几何模型的建立
依据现场生产时采用的轧制工艺和参数建立有限元模型,货叉扁钢精轧过程采用450轧机5道次连轧的方式进行。奇数道次为平辊轧制,偶数道次为箱型孔立轧,箱型孔尺寸如图1所示。由于扁钢轧制为对称模型,所以为节约计算时间,建立1/4轧制模型,轧件XY和XZ面为对称面,-X向为轧制方向。轧件尺寸H×B×L=35 mm×62.5 mm×500 mm。各道次轧辊尺寸、转速等如表1所示,利用DEFORM软件建立的扁钢轧制模型如图2所示。

图1 箱型孔尺寸

道次辊缝/mm压下率/%轧辊外径/mm工作直径/mm轧辊转速/rpm15521.43425425.8355.492129.02480372.8267.2234521.05435435.0569.094105.16480372.1584.38540.412.17445444.8177.29

图2 轧制模拟图形
2.2材料选取及基本属性
在DEFORM仿真过程中,选取与某钢厂现场轧制时所选用材料属性相似的35号钢进行模拟试验,在DEFORM材料库中选取对应材料为AISI-1 035[1 300-2 000F(700-1 100 ℃)]。
化学成分:C—0.32%~0.40%,Si—0.17%~0.37%,Mn—0.50%~0.80%,S—0.035%,P—0.035%,Cr—0.25%,Ni—0.25%,Cu—0.25%。
机械性能:抗拉强度≥530 MPa,屈服强度≥315 MPa,伸长率≥20%,断面收缩率≥45%。
流动应力曲线:为保证高精度轧制,在模拟计算过程中考虑了材料流动应力随着温度和应变值的变化,由DEFORM材料库得到35号钢的流动应力参数曲线如图3所示。

图3 35号钢的流动应力
2.3初始条件和边界条件的设置
初始条件:现场生产时采用加热炉对扁钢加热,出炉后经过大概15 s的时间开始连轧。对初始加热温度设置为850 ℃、900 ℃、950 ℃、1 000 ℃、1 050 ℃。为保证高精度轧制,按照轧件开轧时的实际温度分布对轧件进行初始温度设置。以加热到950 ℃时为例,开轧时轧件内部和外部温度分布如图4所示。
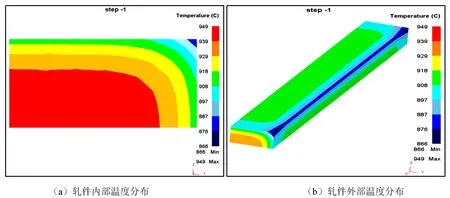
图4 轧件内部温度分布
边界条件:由于轧件为1/4模型,轧件XZ和XY2个面为对称面,其余4个自由面与周围环境产生的对流和辐射换热,设置轧件与空气的综合换热系数α=0.17 kW/(m2·℃),设置轧件与轧辊之间的热传递系数为11 kW/(m2·℃)。
接触条件:本文采用库伦摩擦,数值取0.3、0.35、0.4、0.45、0.5。
3 模拟结果分析
因为在平辊轧制和孔型轧制时金属流动规律不一致,所以在分析平辊轧制道次金属流动规律时选择第1道次为研究对象,分析孔型轧制时选择第2道次为研究对象。
3.1平辊轧制道次速度场的分布
(1)第1道次轧制时的Y向速度云图
第1道次轧制时变形区横截面上的Y向速度如图5所示。

图5 第1道次Y向速度云图
由图5可以得到:轧件Y向速度均为正值,即轧制变形区各点向轧件外侧流动,且各点的Y向速度由对称面到两外侧逐渐增大。随着温度的升高,变形区相同区域Y向速度和最大速度均逐渐增大。不同摩擦系数时的速度分布也是如此,但是随着摩擦系数的增大,变形区相同区域的Y向速度和最大速度均逐渐减小。
(2)第1道次轧制时的Y向速度曲线图
利用DEFORM软件后处理当中的点追踪法,在轧件XY对称面的中心轴上,沿轧件的宽度方向由中心向外侧间隔相等距离依次选取10个数据点,收集数据点的Y向速度值。数据点位置如图6所示。
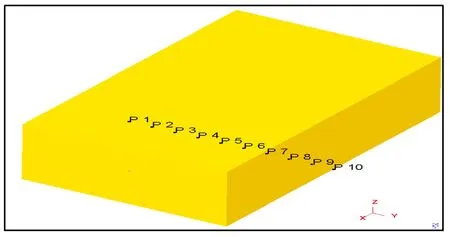
图6 数据点位置

图7 平辊轧制道次Y向速度
图7所示为第1道次轧制时的Y向速度曲线图。由图7可以得到:相同温度或相同摩擦系数时,第1道次轧制时P1~P10各点的Y向速度逐渐增大,由于轧件心部温度较高,金属流动性能好,所以靠近轧件心部的P1~P7的速度呈直线增长。轧件外侧温度低于轧件心部,所以外侧区P8~P10的Y向速度增长缓慢;由图7(a)得到,随着温度的升高,选取各点的Y向速度和相邻两点的速度差均逐渐增大;由图7(b)得到,随着摩擦系数的增大,各点的Y向速度和相邻两点的速度差均逐渐减小。
3.2箱型孔轧制道次速度场的分布
(1)第2道次轧制时Z向速度云图
与平辊轧制道次不同,箱型孔轧制道次Z向为宽展方向。第2道次轧制时Z向速度如图8所示。由图8可以得到:在箱型孔轧制时,轧件呈现明显的双鼓形,各点Z向速度均为正值,即变形区各点由中心向轧件的上下两侧流动,流动速度由中心到上下两侧逐渐增大。随着温度的升高,变形区相同位置区域的Z向速度和Z向速度的最大值均逐渐增大。
在不同摩擦系数条件下轧件变形区的速度分布也是如此,且随着摩擦系数的增大,变形区相同位置区域的Z向速度和Z向速度的最大值均逐渐减小。

图8 第2道次Z向速度云图
(2)第2道次轧制时Y向速度云图

图9 第2道次Y向速度云图
由图9可以得到:在箱型孔轧制时,变形区的各点Y向速度均为负值,即变形区各点由两侧向中心流动,并且流动速度由中心到两侧逐渐减小;随着温度的升高,变形区相同区域的Y向速度和Y向速度的最小值均逐渐减小。
在不同摩擦系数条件下轧件变形区的速度分布也是如此,且随着摩擦系数的增大,变形区相同位置区域的Y向速度和Y向速度的最大值均增大。
3.3宽展系数的拟合公式
通过测量轧件在不同参数下各道次的宽度尺寸,计算轧件的宽展系数,并通过曲线拟合的方式,分别给出轧件在模拟参数范围内宽展系数关于温度和摩擦系数的计算公式,为现场优化工艺参数提供依据。
(1)温度对尺寸精度的影响
选取摩擦系数为0.4,温度为850 ℃、900 ℃、950 ℃、1 000 ℃、1 050 ℃的数据组,测量不同温度下经过第1道次轧制后轧件的宽度尺寸,然后根据宽展系数公式(1)计算出不同温度下第1道次轧件的宽展系数,然后进行曲线拟合,如图10所示,得到宽展系数关于温度的拟合曲线公式(2)。
(1)
式中:
ω—宽展系数;
b—轧件变形后尺寸;
B—轧件变形前尺寸。
ω=0.253 06+0.001 43T-6.285 7×10-7T2
(2)
式中:
ω—宽展系数;
T—轧制温度。

图10 不同温度下的宽展系数拟合曲线 图11 不同摩擦系数下的宽展系数拟合曲线
(2)摩擦系数对尺寸精度的影响
选取温度为950 ℃,摩擦系数分别为0.3、0.35、0.4、0.45、0.5的数据组,将不同摩擦系数下的第1道次宽展系数进行拟合,如图11所示,得到宽展系数关于摩擦系数的拟合曲线公式(3)。
ω=1.134 11-0.341 43μ+0.314 29μ2
(3)
式中:
ω—宽展系数;
μ—摩擦系数。
4 结论
(1)无论是平辊轧制还是箱型孔轧制道次,轧件变形区宽展方向的速度均呈圆弧形分布,且均为正值,并由中心区域向两侧逐渐增大。在箱型轧制时轧件出现明显的双鼓形状,符合轧制变形的一般规律。
(2)变形区相同区域各点的宽展方向速度和最大宽展速度随着温度的升高均逐渐增大,随着摩擦系数的增大均逐渐减小。
(3)对不同参数下的宽展系数曲线进行拟合,在模拟参数范围内分别得到了宽展系数关于温度和摩擦系数的拟合公式,作为现场生产计算各道次轧件宽度的依据。
[1]丁文华, 李淼泉, 姜中行, 等. 中厚板轧制过程的数值模拟[J]. 轧钢, 2010, 27(6):15-21.
[2]赵阳, 杨荃, 何安瑞, 等. 高精度中厚板平面形状预测模型的研究及应用[J]. 钢铁, 2011, 09:55-58+63.
[3]姚世泽. 扁钢精轧过程数值模拟仿真与分析[D]. 浙江:浙江工业大学, 2013.
[4]赵章风, 姚世泽. 扁钢精轧过程数值模拟仿真与分析[J]. 机电工程, 2014, 31(3):271-282.
[5]董连超. 变厚度轧制金属流动规律[D]. 燕山大学, 2013.
[6]刘恩洋. 板带钢热连轧高精度轧后冷却控制的研究与应用[D]. 辽宁:东北大学, 2012.
Numerical Simulation of Metal Flow Law of Fork Flat Steel during Finishing Rolling Process
DU Jin-long1, ZHANG Gui-jie1, WANG Li-ya2
(1.College of Metallurgy and Energy, North China University of Science and Technology, Tangshan Hebei 063009, China;2. College of Science, North China University of Science and Technology, Tangshan Hebei 063009, China)
flat steel; finishing rolling; metal flow law; spread coefficient; numerical simulation
To better control the dimensional accuracy of fork flat steel and eliminate subsequent processing, the hot continuous rolling model of fork flat steel was built according to the process of a rolling factory. The model of hot continuous rolling of fork flat steel was established and the finishing rolling process of flat steel was simulated based on finite element software DEFORM. The effects of different temperature and friction coefficients on metal flow law were studied on basis of simulation results, and the mathematical models of spread coefficient of fork steel were obtained by means of curve-fitting. These models provide reliably theoretical basis for the establishment of reasonable process parameters and the improvement of dimensional accuracy of the product.
2095-2716(2016)03-0038-09
TG335.11
A

