二维数字阵列三阶泰勒展开单脉冲角度估计

马晓峰, 冯丹萍,2, 盛卫星, 韩玉兵, 张仁李

(1. 南京理工大学电子工程与光电技术学院, 江苏 南京 210094；2. 中航工业雷华电子技术研究所，江苏 无锡 214063)



二维数字阵列三阶泰勒展开单脉冲角度估计

马晓峰1, 冯丹萍1,2, 盛卫星1, 韩玉兵1, 张仁李1

(1. 南京理工大学电子工程与光电技术学院, 江苏 南京 210094；2. 中航工业雷华电子技术研究所，江苏 无锡 214063)

全数字或相控阵子阵结构的数字单脉冲测角一般都采用基于单脉冲比一阶泰勒展开的测角公式,主瓣干扰下的自适应数字单脉冲测角也采用鉴角曲线斜率约束的方法,这些都会导致和波束主瓣宽度内偏离波束指向较远目标的测角偏差增大。为了解决上述问题,针对任意二维数字阵列结构,推导了基于单脉冲比三阶泰勒展开的二维单脉冲测角公式,分析了公式求解的收敛问题。仿真结果表明所提方法对和波束主瓣范围内的目标均有较小的测角偏差,可以有效地提高主瓣干扰下的测角性能。该方法在提高测角性能的同时运算量增加不大,适合工程实现。

二维数字阵列; 单脉冲角度估计; 泰勒展开; 测角偏差; 主瓣干扰

0　引　言

和差单脉冲技术能够精确地测量目标的角度信息,因此被广泛应用于预警和跟踪雷达等系统。全数字或相控阵子阵结构数字阵列采用的数字单脉冲测角方法一般都是基于单脉冲比一阶泰勒展开(下面简称一阶展开)的[1-2],鉴角曲线用一定斜率的直线逼近,由于理想鉴角曲线在偏离波束指向角度较远处存在较大的非线性,这些位置的测角偏差较大。为了扩大线性测角范围,并减小存在主瓣干扰的条件下,自适应单脉冲鉴角曲线的非线性,有文献提出在偏离波束指向处采用三点或者多点斜率约束的方法优化差波束方向图[3-5],但是额外增加的约束会减少自适应算法的自由度,导致自适应差波束输出的信干噪比下降,可能改变差波束方向图的形状,使得差波束的副瓣电平恶化,而且该方法扩大目标线性测角区间的范围也比较有限。针对鉴角曲线不精确引起的测角偏差问题,传统的单脉冲测角系统也有采用鉴角曲线直接存储或者近似的解决方法[6],这种方法对于指向精度不高的一维单脉冲测角系统比较适用,而高指向精度的二维大阵列单脉冲测角系统,波束指向为二维角度,且每个角度均需要存储理想的鉴角曲面,存储数据量大,灵活性比较差[7]。

文献[8]针对一维数字阵列结构,提出了采用单脉冲比三阶泰勒展开(下面简称三阶展开)的自适应单脉冲测角方法,使得一维鉴角曲线以三次多项式的形式逼近理想鉴角曲线,和波束主瓣宽度内,在目标偏离波束指向较远处仍保持较小的测角偏差。还有文献给出单脉冲比更高阶泰勒展开的自适应单脉冲测角方法[9]。本文针对任意二维数字阵列结构,详细推导了基于三阶展开的二维单脉冲测角公式,考虑到阵列结构的对称性,简化测角公式,接着,采用牛顿迭代法计算角度估计值,并分析了采用牛顿迭代法仅需要几次迭代就可以获得精确角度估计值的原因。仿真结果表明,基于三阶展开的二维单脉冲角度估计方法,在和波束主瓣宽度内具有均匀的测角偏差,测角偏差优于一阶展开的方法;该方法还十分适用于主瓣干扰情况下,全数字或相控阵子阵结构数字阵列的自适应单脉冲角度估计。

1　问题模型

1.1阵列模型与测角公式

如图1所示,假设平面阵列天线的N个各向同性的单元天线位于极坐标系的yoz平面内,第i个单元天线的位置为ri=(0,yi,zi)T。平面波来波的单位方向性矢量为U=(w,u,v), 其中,w=sinθcosφ,u=sinθsinφ,v=cosθ,θ为与z轴夹角,φ为xoy平面内与x轴夹角。x轴(θ,φ)=(90°,0°)为波束指向法线方向,目标角度估计范围为θ:0°～180°,φ:-90°～90°。则第i个单元天线接收到的复基带信号为

(1)

式中,b为回波复幅度;λ为工作波长;ni为第i个单元天线输出的复高斯白噪声信号。回波信号复向量可以表示为

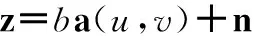
(2)

式中,a(u,v)为(u,v)方向的导向性矢量,ai(u,v)=ej(2π/λ)(yiu+ziv)(i=1,…,N);复高斯白噪声向量n的均值为0,方差为σ2I；b的最大似然估计可以通过最大化如下的高斯概率密度函数获得

(3)

因此,b的最大似然解为

(4)

式中，(·)H为共轭转置；U的最大似然估计值为式(5)给出的和波束扫描功率对数方向图的最大值对应的角度[1-2]。

(5)

式中,w(u,v)为和波束的权重系数。当和波束为静态波束时,w(u,v)=a(u,v);当和波束为自适应波束时,w(u,v)=μR-1a(u,v),μ=1/aH(u,v)R-1a(u,v)为一个标量系数,R-1为阵列接收复基带信号的协方差矩阵估计的逆。

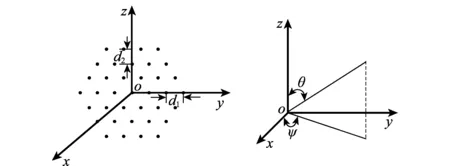
图1　均匀平面阵列结构示意图

记 F(u,v)的一阶偏导数为Fα：

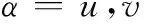
(6)

式中,Fu,Fv就是u,v方向的单脉冲比；wu,wv为和波束权重系数在u,v方向的偏导数,即u,v方向差波束的权重系数。

假设,目标方向(us, vs)在阵列天线和波束指向(u0, v0)附近,将单脉冲比Fα在(u0, v0)处进行三阶泰勒展开,可得

(7)

式中,Fαβ,Fαβγ,Fαβγδ(α,β,γ,δ可取值为u,v)分别为和波束对数功率方向图F(u,v)的二阶、三阶和四阶偏导数。通过求解公式(7)就可以得到目标方向(us, vs)的精确估计,本论文第三部分将推导公式(7)所有系数的计算方法,给出采用牛顿迭代法求解目标角度估计值的过程,并分析牛顿迭代法的收敛性。

1.2二维角度估计的克拉美罗界

为了对本文提出方法的测角性能进行有效评估,下面给出二维角度估计的克拉美罗界。克拉美罗界确定了任何无偏估计量的最小方差。

以估计u值为例,克拉美罗不等式为

(8)

式中

(9)

将式(9)代入式(8),可以得到测量所得u偏离实际角度us的方差的下界。

同理可以得到v偏离实际角度vs的方差的下界。

2　单脉冲比三阶泰勒展开方法

由式(6)给出的和波束对数功率方向图F(u,v)的一阶偏导数Fα的计算公式可以知道,当忽略接收机的噪声分量,即z≈ba(u,v)时,若设波束指向角度的导向矢量为权矢量,则Fα在(u0,v0)处的值为0。文献[10]指出,对于高增益大规模阵列天线(如902阵元的阵列),当阵元信噪比低于-10dB时,忽略噪声分量会有较大的影响,但是在太低的信噪比条件下,任何单脉冲角度估计方法都是不可用的。因此,我们仅考虑实际单脉冲角度估计可以使用的场合,比如经过积累处理后的和波束输出信噪比大于10dB的情况,此时可以忽略噪声分量。在后续推导F(u,v)的二阶、三阶和四阶偏导数Fαβ,Fαβγ,Fαβγδ(α,β,γ,δ可取值为u,v)时,都将忽略接收机噪声的影响。推导得到的各项系数值都是在波束指向角度(u0,v0)处的值。

(10)

h=wHzzHw

(11)

式中,g[α](α=u,v)表示α方向的差波束功率。

则F(u,v)的二阶偏导数为

(12)

F(u,v)的三阶偏导数为

(13)

四阶偏导数可以表示为

(14)

其中

(15)

(16)

(17)

(18)

式(15)～(18)中

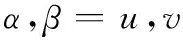
(19)

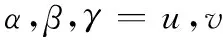
(20)

(21)

(22)

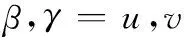
(23)

(24)

为了后面计算方便,令

(25)

(26)

将计算所得系数代入式(7)的三阶展开测角公式中,解二元三次方程就可以计算目标方向(us,vs)。

需要指出,式(25)和式(26)中的各个值,在波束指向角度(u0,v0)处的取值仅与阵元的坐标位置ri=(0,yi,zi)(i=1,2,…,N)有关,当二维阵列阵元位置中心对称时(一般都能满足),可以得到如下结论

(27)

(28)

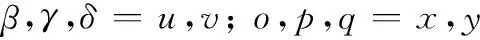
(29)

(30)

式中，α,β,γ,δ=u,v,且u的个数为奇数;o,p,q,s=x,y。

(31)

(32)

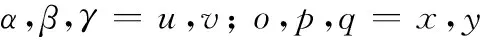
(33)

(34)

式中，α,β,γ,δ=u,v,且u的个数为奇数;o,p,q,s=x,y。

因此,将式(27)～式(34)代入式(19)～式(24)后可以看到,F(u,v)的二阶、三阶和四阶偏导数中,除以下系数外其余系数均为0。

(35)

(36)

(37)

(38)

(39)

(40)

所以,基于三阶展开测角公式(7)可以简化为

(41)

可以看到,式(41)中二次项系数全为0,因此,单脉冲比二阶泰勒展开的测角结果与一阶展开的结果是一样的。

3　角度估计值求解与收敛性分析

三阶展开式(41)是一个典型的非线性方程组,可以采用牛顿迭代法求解,定义函数向量

(42)

则式(41)的解即为l(us,vs)=0的解。

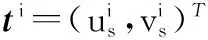
(43)

于是,得到牛顿迭代法的迭代公式为

(44)

迭代公式的初始值可以设定为和波束指向(u0,v0),由于目标方向(us,vs)靠近和波束指向(u0,v0),经过几次迭代就可以收敛。

使用式(44)计算得到的第1次迭代结果为

(45)

式中

(46)

(47)

将式(46),式(47)代入式(45),得

(48)

从式(48)可以看到,第一次牛顿迭代得到的结果等价于一阶展开测角公式求解得到的结果。

下面以函数l1(us,vs)为例,分析一下采用上述牛顿迭代法的收敛性。

定理 1[11]设函数f(x)满足f(x*)=0,f′(x*)≠0且f(x)在x*的领域内有二阶连续导数,则当初值x0足够接近于x*时,由牛顿迭代公式得到的序列至少是二阶收敛的。

l(us,vs)的二阶导数仍为初等函数,故其在us的领域Bδ(us)=[us-δ,us+δ]是连续的,并且

(49)

(50)

则以任意初值us0∈Bδ(us),由牛顿迭代法得到的序列至少二阶收敛于us。

由于牛顿迭代法的局部收敛性,故初值的选取非常重要。在解式(41)时,我们取和波束指向方向(u0,v0)为初值,第一次牛顿迭代的结果与一阶展开的测角结果完全相同,已经很接近实际值,所以牛顿迭代法能快速收敛。

4　仿真结果分析

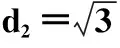
4.1无干扰条件下测角性能

仿真设置的阵元信噪比为20dB,噪声是均值为0,方差为1的高斯白噪声。

仿真 1假设和波束中心指向为(θ0,φ0)=(60°,0°),即(u0,v0)=(0,0.5),图2(a)和图2(b)分别给出了目标处于和波束3dB波束宽度内及其附近不同位置,三阶展开和一阶展开的测角性能。箭头的起点为目标真实角度,每个角度进行500次蒙特卡罗仿真,每次仿真得到的测角结果在图中用小圆圈标出,箭头的终点为500次角度估计结果的均值。从小圆圈的分布范围可以看出测角方法的测角精度,而从箭头的长短可以看出测角方法的测角偏差。

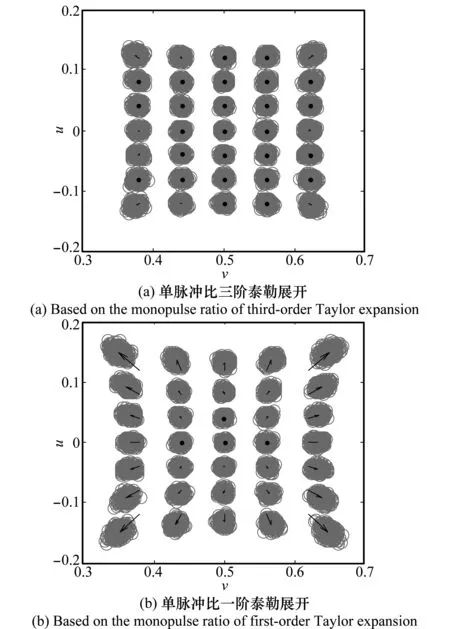
图2　和波束指向(u0, v0)=(0, 0.5)时的测角性能比较

从图2可以看出,和波束波束宽度范围内,当目标角度偏离和波束指向角度较远时,三阶展开具有更小的测角偏差,这是因为三阶展开测角方法的鉴角曲面采用三次多项式的形式逼近理想的鉴角曲面,当目标偏离波束指向角度较大时仍具有较好的近似。图3给出了u方向的鉴角曲面切图,当目标角度偏离波束指向角度较远(仍在主瓣3 dB宽度范围内)时,一阶展开鉴角曲线已经偏离了理想鉴角曲线,而三阶展开仍能较好的逼近理想情况,因此测角性能更好。

另外,从每个角度500次测角结果的分布来看,测角精度差别不大,u方向或者v方向的测角精度可由如下计算公式估算得到[12]

(51)

式中,k为常数,只与阵元结构有关,u3 dB为和波束3 dB波束宽度,SNRout为和波束输出信噪比(signal to noise ratio,SNR)。两种测角方法在和波束指向附近的500次测角方差与式(51)吻合,差别不大,但一阶展开方法在偏离和波束指向较远处的测角方差逐渐增大,主要还是由于鉴角曲面误差卷入引起的。

图3　和波束指向(u0, v0)=(0, 0.5),固定 v=0.5时, u方向的鉴角曲线　

为了更清楚地比较一阶展开和三阶展开测角性能差异,表1给出了和波束3 dB波束宽度内及其附近的部分角度位置,500次统计平均得到的实测角度和实际角度夹角。

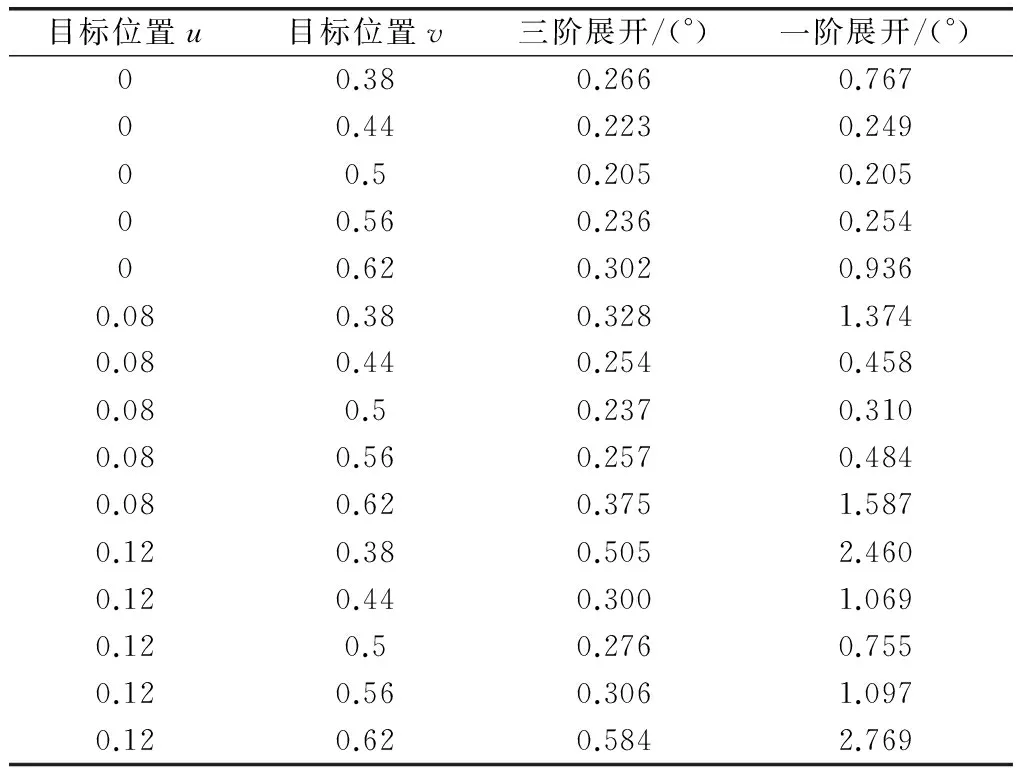
表1　无干扰情况下一阶展开和三阶展开测角结果

从表1中可以看到,目标离波束指向很近时,三阶展开和一阶展开两种方法测角偏差均值相当,随着目标偏离波束指向,三阶展开的测角偏差均值明显小于一阶展开。

仿真 2为了比较一阶展开和三阶展开在整个测角区间的测角性能,我们设置波束指向方位角φ=0°,俯仰角θ在45°～135°范围内以1°为步进扫描,计算每个波束指向角度下,目标处于和波束3 dB波束宽度内及其附近任意位置的平均测角偏差,如图4所示。

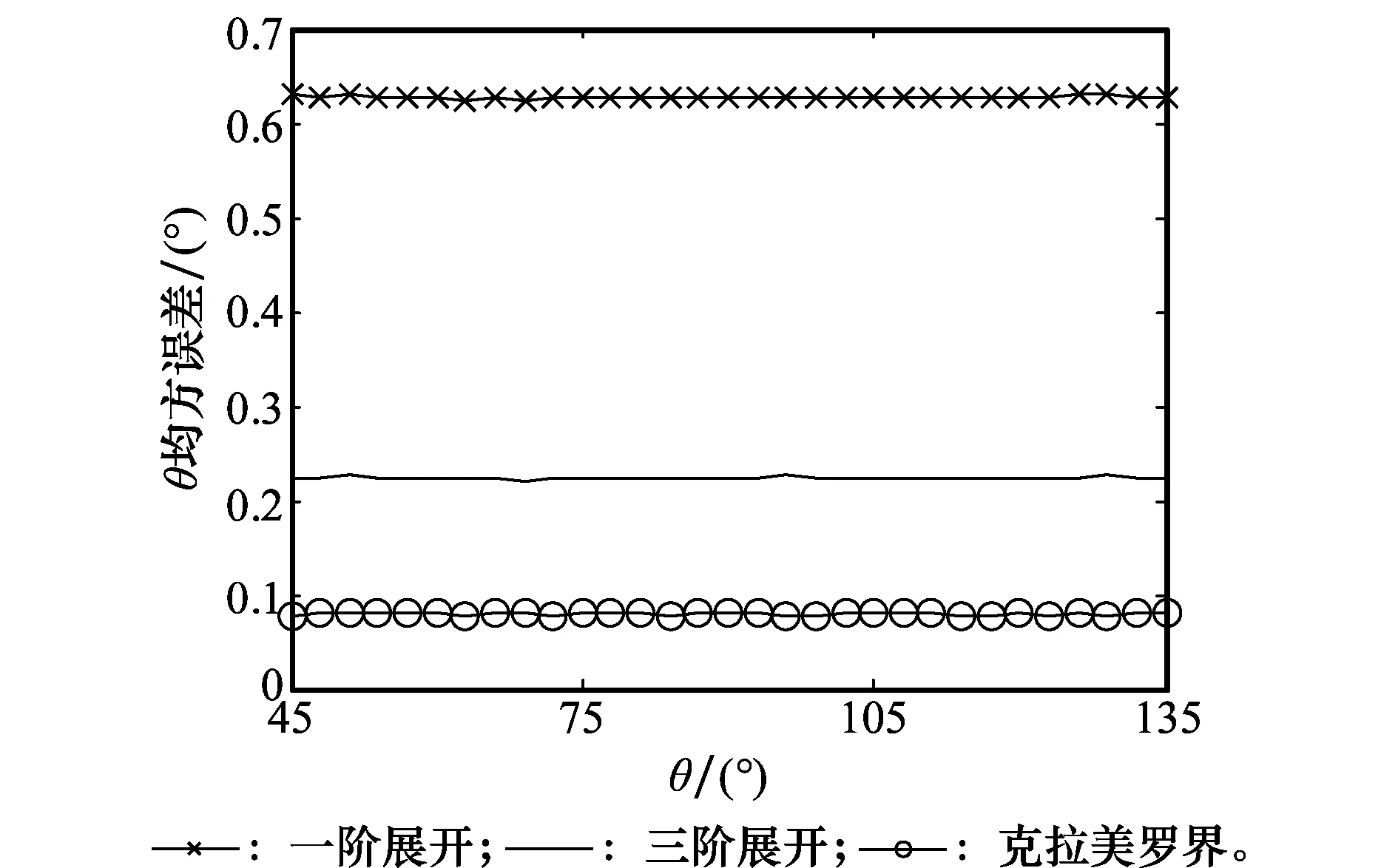
图4　φ=0°时θ方向的平均测角误差比较

从图4可以看到,两种方法在θ变化时测角性能变化不大,三阶展开的测角偏差在整个测角区间始终比一阶展开好,更逼近克拉美罗界。

4.2干扰条件下测角性能

仍然以图1所示二维阵列为例,给出三阶展开测角方法应用于自适应单脉冲系统的测角性能。仿真条件为,阵元信噪比20 dB,阵元干噪比40 dB,干扰和信号互不相关,噪声为均值为0,方差为1的高斯白噪声。和波束与差波束的自适应权重系数均采用线性约束最小方差准则优化得到[10]。

仿真 3旁瓣干扰条件下测角性能仿真。和波束中心指向为(θ0,φ0)=(60°,0°),即(u0,v0)=(0,0.5);干扰方向角度(θJ,φJ)=(60°,35.26°),即(uJ,vJ)=(0.5,0.5),图5给出了v=0.5时,u方向的鉴角曲面切图。可以看到,存在旁瓣干扰情况下,三阶展开鉴角曲线可以更好的逼近理想鉴角曲线,由于旁瓣干扰的抑制对主瓣区域的形状影响较小,鉴角曲线与无干扰情况下的鉴角曲线接近,因此角度估计精度和偏差也与无干扰情况下的类似,此处不再给出仿真结果。

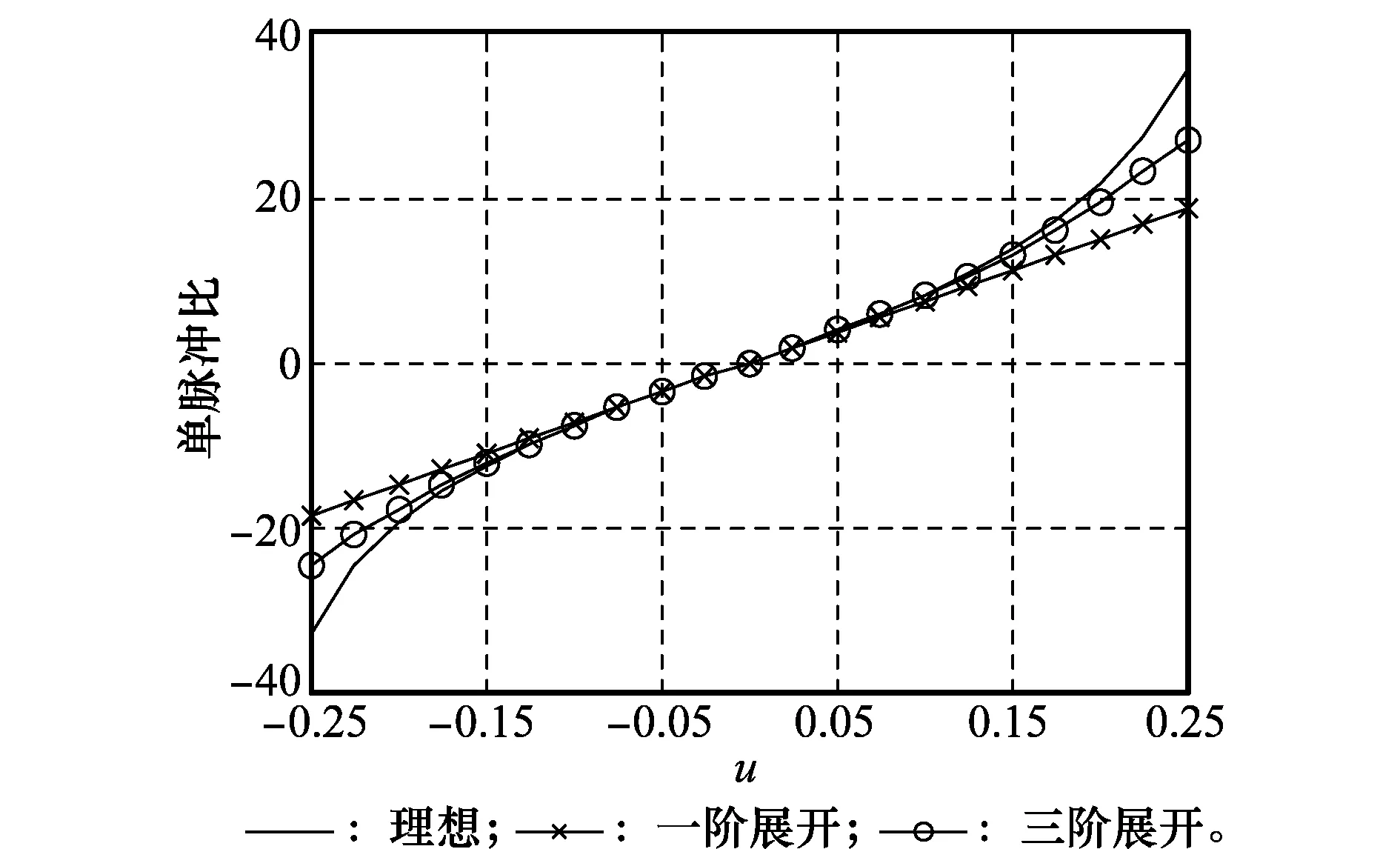
图5　和波束指向(u0,v0)=(0,0.5),旁瓣干扰方向(uJ,vJ)=(0.5,0.5),固定v=0.5时,u方向的鉴角曲线　

仿真 4主瓣干扰条件下测角性能仿真。和波束中心指向为(θ0,φ0)=(60°,0°),即(u0,v0)=(0,0.5);干扰方向角度(θJ,φJ)=(60°,13.35°),即(uJ,vJ)=(0.2,0.5),图6给出了v=0.5时,u方向的鉴角曲面切图。可以看到存在主瓣干扰的情况下,由于和波束及差波束方向图在主瓣区域,特别是在干扰角度附近严重变形,鉴角曲线发生较大的畸变,一阶展开方法逼近理想鉴角曲线的误差变大,而三阶展开方法除了干扰角度附近外逼近仍然良好。

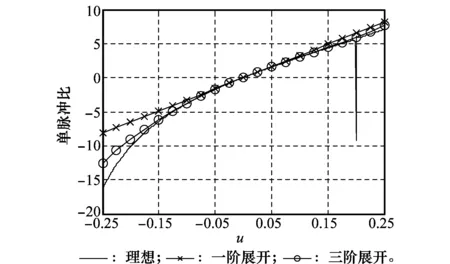
图6　和波束指向(u0, v0)=(0, 0.5),主瓣干扰方向(uJ, vJ) (0.2, 0.5),固定v=0.5时,u方向的鉴角曲线 Fig.6　Monopulse ratio of u when sum beam points to (u0, v0)=(0, 0.5), v=0.5 and the mainlobe interface located at (uJ, vJ)=(0.2, 0.5)

图7(a)和图7(b)分别给出了目标在和波束3 dB波束宽度范围内及其附近时,三阶展开和一阶展开的测角性能。每个角度同样进行500次蒙特卡罗仿真。

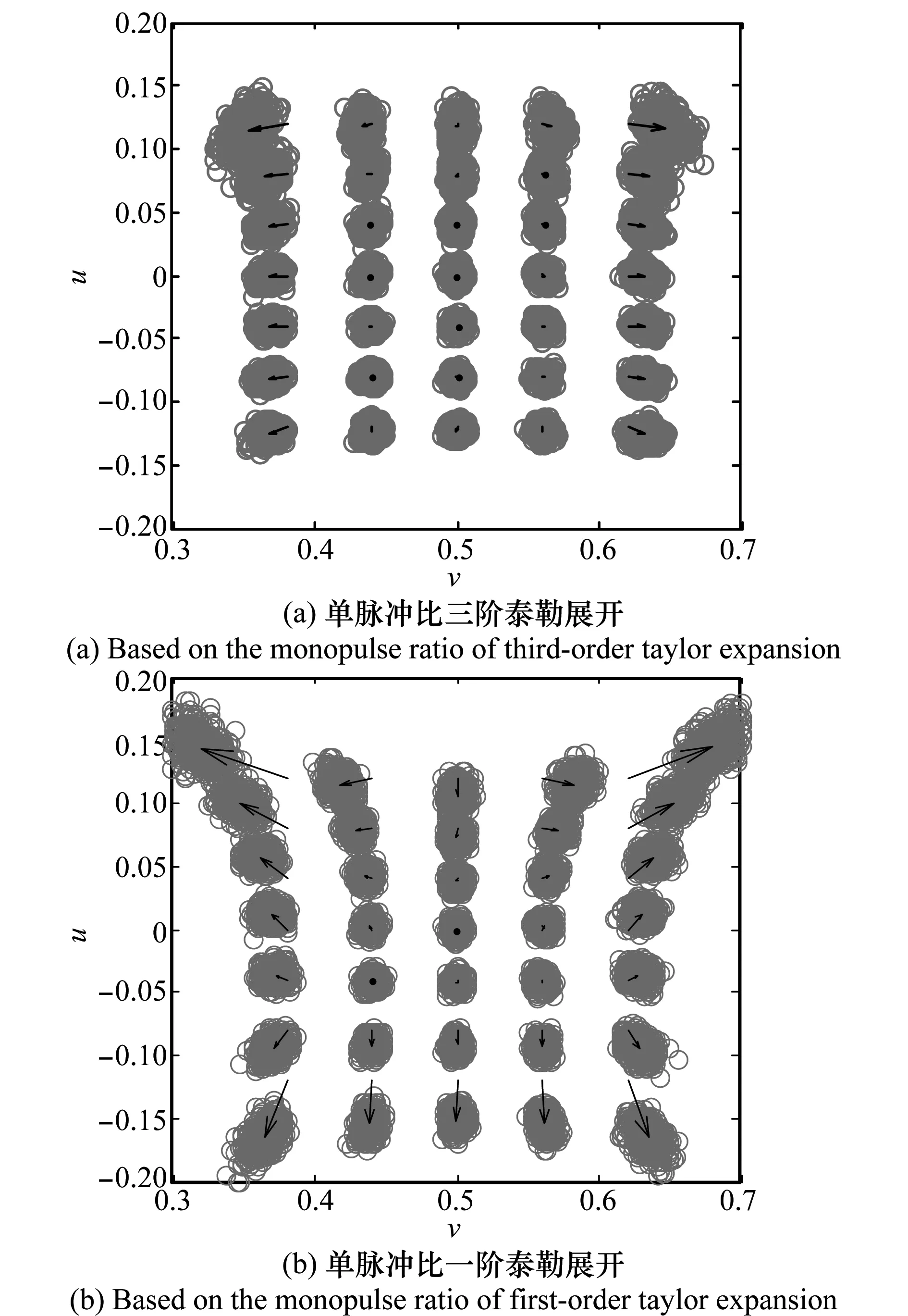
图7　和波束指向(u0, v0)=(0, 0.5),主瓣干扰方向(uJ, vJ) (0.2, 0.5)时的测角性能比较　　　　　　　 Fig.7　Comparison of angle estimation performace when sum beam points to (u0, v0)=(0, 0.5) and the mainlobe interface located at (uJ, vJ)=(0.2, 0.5)

从图7可以看出,当存在主瓣干扰时,三阶展开方法测角性能保持较好,仅在干扰角度附近测角偏差和测角精度有所降低,而一阶展开方法在主瓣区域内偏离和波束指向角度,特别是主瓣干扰附近角度,测角偏差和测角精度都明显降低,测角稳健性较差。

同样,表2给出了和波束3 dB波束宽度内及其附近的部分角度位置,500次统计平均得到的实测角度和实际角度夹角。

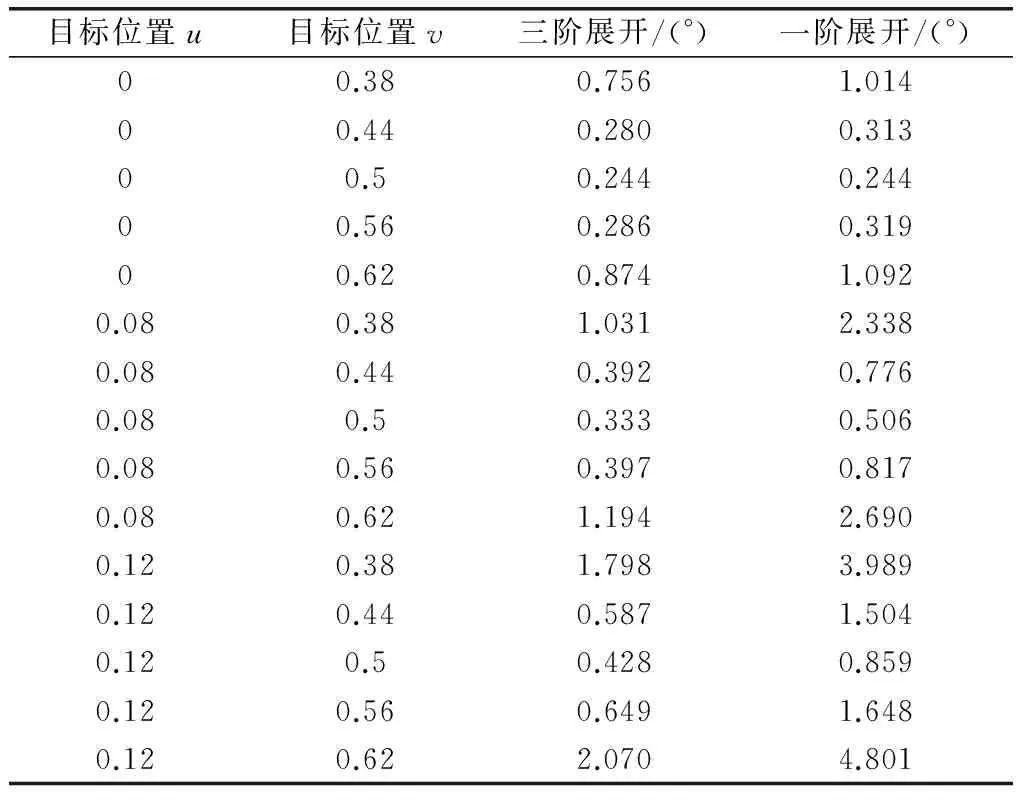
表2　主瓣干扰情况下一阶展开和三阶展开测角结果

从表2中可以看到,当存在主瓣干扰时,三阶展开的测角偏差更小。另外从表1和表2的测角结果可以看到,当存在干扰时,两种方法各自的测角误差都有所增大。

5　结　论

本文针对任意二维数字阵列结构,推导了基于单脉冲比三阶泰勒展开的二维单脉冲测角简化公式及其快速迭代求解算法,并分析了迭代算法的收敛性。采用该方法的单脉冲鉴角曲面与理想鉴角曲面逼近程度优于单脉冲比一阶泰勒展开的方法,因此针对和波束主波束宽度范围内的目标均具有明显优于单脉冲比一阶泰勒展开的方法的测角偏差。同时,该方法还十分适用于提高主瓣干扰情况下自适应单脉冲算法的角度估计精度及其稳健性。

[1] Nickel U. Overview of generalized monopulse estimation[J].IEEEAerospaceandElectronicSystemsMagazine,2006,21(6):27-55.

[2] Nickel U. Monopulse estimation with adaptive arrays[J].IEEProceedings-Radar,SonarandNavigation, 1993, 140 (5): 303-308.

[3] Fante R L. Synthesis of adaptive monopulse patterns[J].IEEETrans.onAntennasandPropagation, 1999, 47(5): 773-774.

[4] Yu K B, David J M. Adaptive digital beamforming for angle estimation in jamming[J].IEEETrans.onAerospaceandElectronicSystems, 2001, 37(2): 508-523.

[5] Li R F, Rao C, Dai L Y, et al. Algorithm for constrained adaptive sum-difference monopulse among sub-arrays[J].JournalHuazhongUniversityofScienceandTechnolgy, 2013, 41(9): 6-10. (李荣锋, 饶灿, 戴凌燕, 等. 子阵间约束自适应和差单脉冲测角算法[J].华中科技大学学报, 2013, 41(9): 6-10. )

[6] Niu B J, Li Y B. Study and application of angle measurement for 2-D phased array monopluse tracking[J].ModernRadar, 2003, 25(5): 16-18.(牛宝君, 李延波. 二维相控阵单脉冲跟踪测角方法的研究与应用[J].现代雷达, 2003, 25(5): 16-18.)

[7] Zhu W, Chen B X, Zhou Q. Angle measurement method with digital monopulse for 2-dimensional digital array radar[J].SystemsEngineeringandElectronics, 2011, 33(7): 1503-1509.(朱伟, 陈伯孝, 周琦. 两维数字阵列雷达的数字单脉冲测角方法[J].系统工程与电子技术, 2011, 33(7): 1503-1509.)

[8] Chen C Z, Wang T,Wu J X. Monopulse angle estimation with adaptive array based on the third-order taylor series[J].ModernRadar,2013,35(8):32-36.(陈成增,王彤,吴建新.基于三阶泰勒展开的自适应单脉冲测角方法[J].现代雷达,2013,35(8):32-36.)

[9] Chen C Z, Wang T, Wu J X, et al. Monopulse angle estimation with adaptive array based on monopulse response curve fitting[J].SystemsEngineeringandElectronics, 2013, 35(7): 1404-1408.(陈成增,王彤,吴建新,等.基于鉴角曲线拟合的自适应单脉冲测角方法[J].系统工程与电子技术,2013,35(7):1404-1408.)

[10] Nickel U. Monopulse estimation with subarray-adaptive arrays and arbitrary sum and difference beams[J].IEEProceedings-Radar,SonarandNavigation, 1996, 143(4): 232-238.

[11] Guan Z, Lu J P.Basicofnumericalanalysis[M]. Beijing: Higher Education Press, 2002. (关治, 陆金甫. 数值分析基础[M]. 北京:高等教育出版社, 2002.)

[12] Xu Z H, Huang Y G, Xiong Z Y, et al. On the consistency of mono-pulse and maximal likelihood estimation with array radar[J].ModernRadar, 2013, 35(10): 32-35.(徐振海, 黄艳刚, 熊子源,等. 阵列雷达单脉冲与极大似然估计的一致性[J].现代雷达, 2013, 35(10): 32-35.)

Third-order taylor expansion based monopulse angle estimation for 2-dimension digital array

MA Xiao-feng1, FENG Dan-ping1,2, SHENG Wei-xing1, HAN Yu-bin1, ZHANG Ren-li1

(1. School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094,China; 2. The Radar and Avionics Institute of Aviation Industry Corporation of China, Wuxi 214063, China)

Digital monopulse angle estimation for full digital or subarray phased array system is generally based on the monopulse ratio first-order taylor expansion, while the monopulse ratio is always linearly constrained in adaptive digital monopulse angle estimation for mainlobe jamming suppression. However, above methods will cause large angle estimation deviation when the target visibly departs from the antenna look direction. In view of the above problems, the 2-dimension monopulse angle estimation formula for arbitrary 2-dimension digital array structure is presented, which is based on the monopulse ratio third-order taylor expansion. The convergence analysis of formula solution is also given. Numerical simulations illustrate that less angle estimation deviation can be obtained for the target within the mainlobe region. It also demonstrates that the target angle estimation performance is improved in the presence of mainlobe jamming. The presented method is suitable for engineering implementation for its less calculation amount.

2-dimension digital array; monopulse angle estimation; Taylor expansion; angle estimation deviation; mainlobe jamming

2015-05-22；

2016-02-21；网络优先出版日期：2016-06-07。

国家自然科学基金(61401207)资助课题

TN 953+.5

A

10.3969/j.issn.1001-506X.2016.08.04

马晓峰(1981-),男,讲师,博士研究生,主要研究方向为阵列信号处理、MIMO雷达信号处理。

E-mail:maxiaofeng@njust.edu.cn

冯丹萍(1991-),女,助理工程师,硕士,主要研究方向为数字阵列角度估计、波束赋形。

E-mail:enny28fdp@126.com

盛卫星(1966-),男,教授,博士,主要研究方向为阵列天线和阵列信号处理、雷达目标电磁散射特性建模及应用、微波成像。

E-mail:shengwx@njust.edu.cn韩玉兵(1972-),男,副教授,博士,主要研究方向为图像处理、阵列信号处理。

E-mail:hanyb@njust.edu.cn

张仁李(1986-),男,讲师,博士,主要研究方向为雷达信号处理。

E-mail:zhangrenli_nust@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160607.1138.004.html