高动态链路中折叠PMF-FFT快速捕获方法
杨秦彪, 王祖林,2, 黄 勤, 裴睿淋
(1. 北京航空航天大学电子与信息工程学院, 北京 100191;2. 地球空间信息技术协同创新中心, 湖北 武汉 430079)
高动态链路中折叠PMF-FFT快速捕获方法
杨秦彪1, 王祖林1,2, 黄勤1, 裴睿淋1
(1. 北京航空航天大学电子与信息工程学院, 北京 100191;2. 地球空间信息技术协同创新中心, 湖北 武汉 430079)
在高动态链路中存在大多普勒频偏,直接序列扩频(direct-sequence spread spectrum,DSSS)接收机必须具有大捕获带宽。现今广泛使用的部分匹配滤波加快速傅里叶变换运算(partial matching filter-fast Fourier transform, PMF-FFT)方法的捕获带宽受限于其FFT运算点数,难以适应高动态场景。因此,提出一种低复杂度大带宽的折叠PMF-FFT捕获方法。该方法首先对接收信号和本地伪码分别作折叠,即分段求和,然后再按照PMF-FFT方法处理。理论分析和仿真结果表明,在更低计算复杂度下,折叠长度为F的折叠PMF-FFT方法的捕获带宽能够达到PMF-FFT方法的F倍。
高动态; 直接序列扩频; 部分匹配滤波加快速傅里叶变换运算; 折叠
0 引 言
直接序列扩频[1-2](direct-sequence spread spectrum,DSSS)通信不仅具有较高的保密性,同时还具有较强的抗干扰能力,现已被广泛应用于军事通信和民用通信领域。DSSS通信系统中的关键技术在于接收机对扩频信号伪噪声(pseudo-noise,PN)码相位和载波多普勒频偏的二维捕获。很多关键应用领域的DSSS通信系统都面临着由于高移动速度带来的高动态通信问题,例如高铁、超高音速飞行器、导弹等。而在高动态环境下,DSSS信号存在很大的多普勒频偏,同时要求接收机具有小的捕获时延。这就要求高动态环境下的DSSS接收机不仅要捕获带宽大,还要捕获时间短。
针对高动态环境下的DSSS信号捕获[3-5]问题,部分匹配滤波加快速傅里叶变换运算(partial matching filter-fast Fourier transform, PMF-FFT)捕获方法[6-10]利用FFT运算一次得到多普勒频偏值,用部分匹配的方式缩短了FFT运算点数,以较短的FFT运算就能完成大多普勒频偏信号的快速捕获,为高动态环境下应用最多的捕获方法。但是该方法必须遍历计算每一个码相位下的相关运算和FFT运算,同时捕获带宽受限于FFT运算点数。在PN码较长时,遍历码相位的计算量显得更为突出。这就降低了PMF-FFT捕获方法在高动态环境中的捕获性能,很多学者也对该方法作了一些改进。文献[11-13]提出,在FFT运算时,预先对数据作补零或加窗处理,改善栅栏效应,以提高频偏捕获的精度;文献[14]采用分组计算FFT的方式,对FFT的计算量进行了优化;文献[15]采用以运算处理速度换取硬件资源消耗的设计思想,减小了PMF-FFT捕获方法硬件实现的资源消耗,但要求系统的时钟频率较高,同时时钟频率直接受限于PN码速率,PN码速率较高时,也带来了高系统时钟下系统设计的困难。以上对PMF-FFT的改进方法主要针对FFT运算和硬件实现两个方面,但是捕获带宽的增加和捕获时间的减少仍然是以硬件资源消耗的增加和计算量的增加为代价的,即目前的改进方法并没有研究如何在不增加硬件资源和计算复杂度的条件下增加捕获带宽。因此,当频偏高达几百kHz时,使用传统的方法会带来巨大的硬件资源消耗和计算量的增加,实际系统很难承受。
针对以上问题,本文借鉴长码捕获中的折叠思想[15],在接收端先对本地PN码和接收信号分别作一定长度的折叠,对折叠后的本地PN码和接收信号再按PMF-FFT方法进行后续的捕获处理。折叠操作成倍的减少了码相位的搜索次数和每一个码相位下的相关运算次数。因此,折叠PMF-FFT方法(简称折叠方法)可以把折叠操作减少的计算量用于增加FFT运算点数,从而能在更低的资源消耗和计算复杂度条件下,成倍的增加其捕获带宽,使得折叠方法更加适用于大多普勒频偏的高动态环境。虽然折叠方法在小多普勒频偏情形下捕获性能比PMF-FFT方法有所下降,但是在大多普勒频偏下其捕获性能显著优于PMF-FFT方法。
1 PMF-FFT捕获方法
PMF-FFT捕获方法采用部分匹配滤波和FFT运算相结合的方式,其捕获原理如图1所示。在每一个本地PN码的起始相位下,经过下变频和下采样后的数据先与本地PN码序列相乘,然后将相乘结果作分段累加,得到P点数据,此部分操作即为部分匹配滤波。利用得到的P点数据作FFT运算并进行谱分析,最大谱峰值对应的PN码相位和多普勒频偏即为正确的捕获结果。
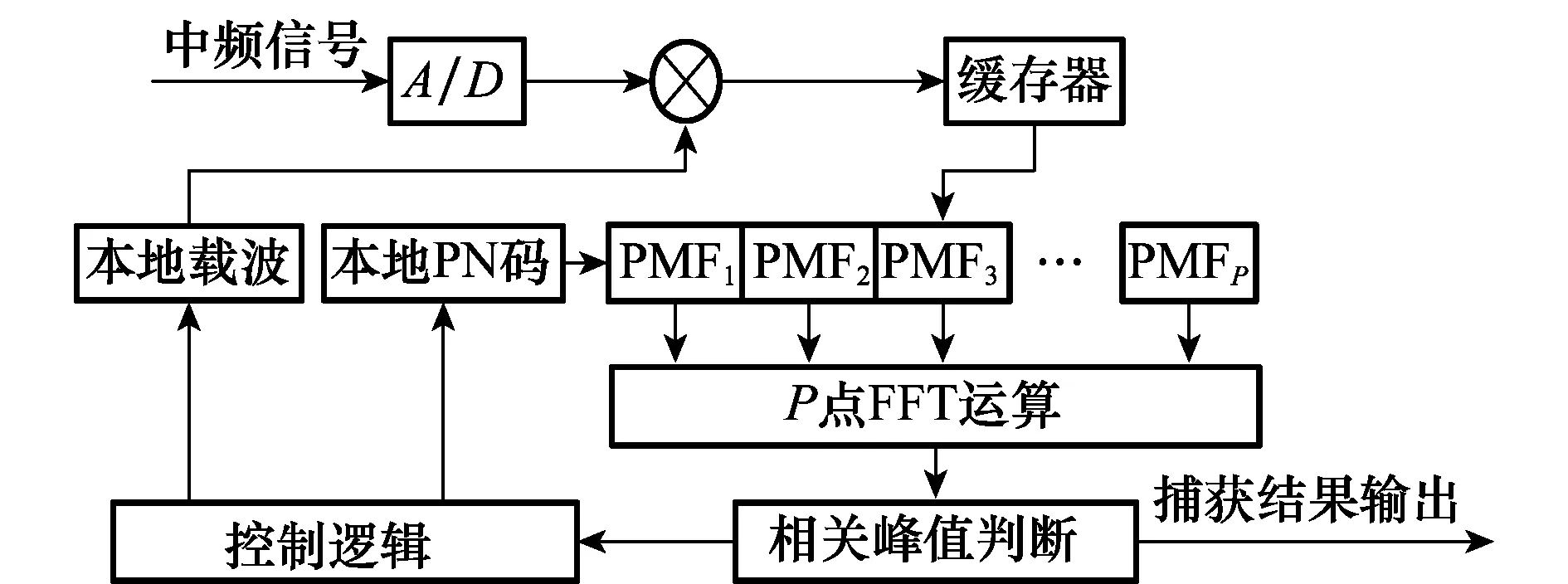
图1 传统PMF-FFT捕获原理图
定义缓存器中存储的接收信号为Si(i=1,2,…,N),N为接收信号长度,本地PN码为Pi(i=1,2,…,N),码周期为L,采样精度为每个码片1个采样点,fd为残留的载波多普勒频偏,Tc为码片宽度,M为每一个PMF的相关长度,P为PMF的个数,也是FFT运算点数,且N=MP。那么每一个PMF的相关结果为
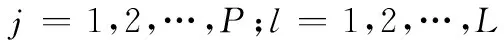
(1)
式中,j表示对应的PMF;l表示本地PN码的起始相位;τ表示接收信号与本地PN码的相位差。在每一个码相位下都会产生P个相关结果,对每一组相关结果作P点FFT运算,即可得到PMF-FFT方法的所有相关结果。
(2)
当l=τ时,接收信号码相位与本地PN码相位对齐,那么在k为与fd对应的索引值处时,GPMF-FFT(τ,k)为所有相关结果中的最大值,此时即可得到当前接收信号的PN码相位τ和多普勒频偏fd,完成捕获。
在不考虑噪声的情况下,令Si=ciexp[j(-2πfdiTc)],ci表示接收信号中的PN码,通过式(1)和式(2)可以得到PMF-FFT关于多普勒频偏fd的归一化频率响应为[13]
(3)
1.1捕获带宽
若对长度为N的信号直接作时域相关,下标DMF(directmatchingfilter,DMF)表示直接匹配滤波,则捕获带宽为
(4)
而PMF-FFT采用部分相关的方式,捕获带宽为
(5)
从式(5)可以看到PMF-FFT的捕获带宽是直接相关的P倍,而P为PMF的个数,亦为FFT的运算点数。即FFT运算点数越大,PMF-FFT方法的捕获带宽越大。
1.2复杂度分析
由图1可以看到,PMF-FFT方法的主要运算在于每一个PN码相位下的相关和FFT运算。定义PN码周期为L,则L个PN码相位下的相关运算(考虑单个实信号)所需的实数乘法和实数加法都为LN;P点FFT运算所需实数乘法和实数加法分别为2P·log2(P)和3P·log2(P),则遍历L个码相位的实数乘法和实数加法运算量为L·2P·log2(P)和L·3P·log2(P)。完成捕获所需的实数乘法量为
(6)
实数加法量为
(7)
由上分析可知,在L和N一定的情况下,相关的运算量远大于FFT运算量。同时,若要增加捕获带宽,只有减小M,即增大FFT运算点数P,这也必然增加计算量和硬件资源消耗。这样就会限制PMF-FFT方法在一些高动态、功率受限以及资源受限等场景下的应用。针对该缺点,本文提出折叠PMF-FFT捕获方法。与PMF-FFT方法相比,在不增加资源消耗的前提下,折叠长度为F的折叠方法的捕获带宽是PMF-FFT方法的F倍,同时还降低了计算复杂度。而在高动态环境下,接收机的捕获带宽和快速捕获是能否成功捕获信号的首要条件。因此,本文提出的折叠方法很适用于高动态环境下的通信信号捕获。
2 折叠PMF-FFT捕获方法
折叠方法借鉴长码捕获中的折叠思想[16],将其用于非长码的捕获中,与PMF-FFT方法相结合,其捕获原理如图2所示。从缓存器读出的接收数据先经过折叠操作,即将数据按设定长度进行分段,然后将每一段内的数据直接求和作为一个新数据,本地PN码亦作同样的处理,对折叠后的数据和PN码再按传统PMF-FFT方法作处理。定义折叠长度为F,F≥2的正整数。那么第一次捕获完成得到的PN码相位实际上为一个包含F个PN码相位的PN码粗捕获区间,再对此粗捕获区间作F次码相位的遍历即可得到精确的PN码相位和多普勒频偏。
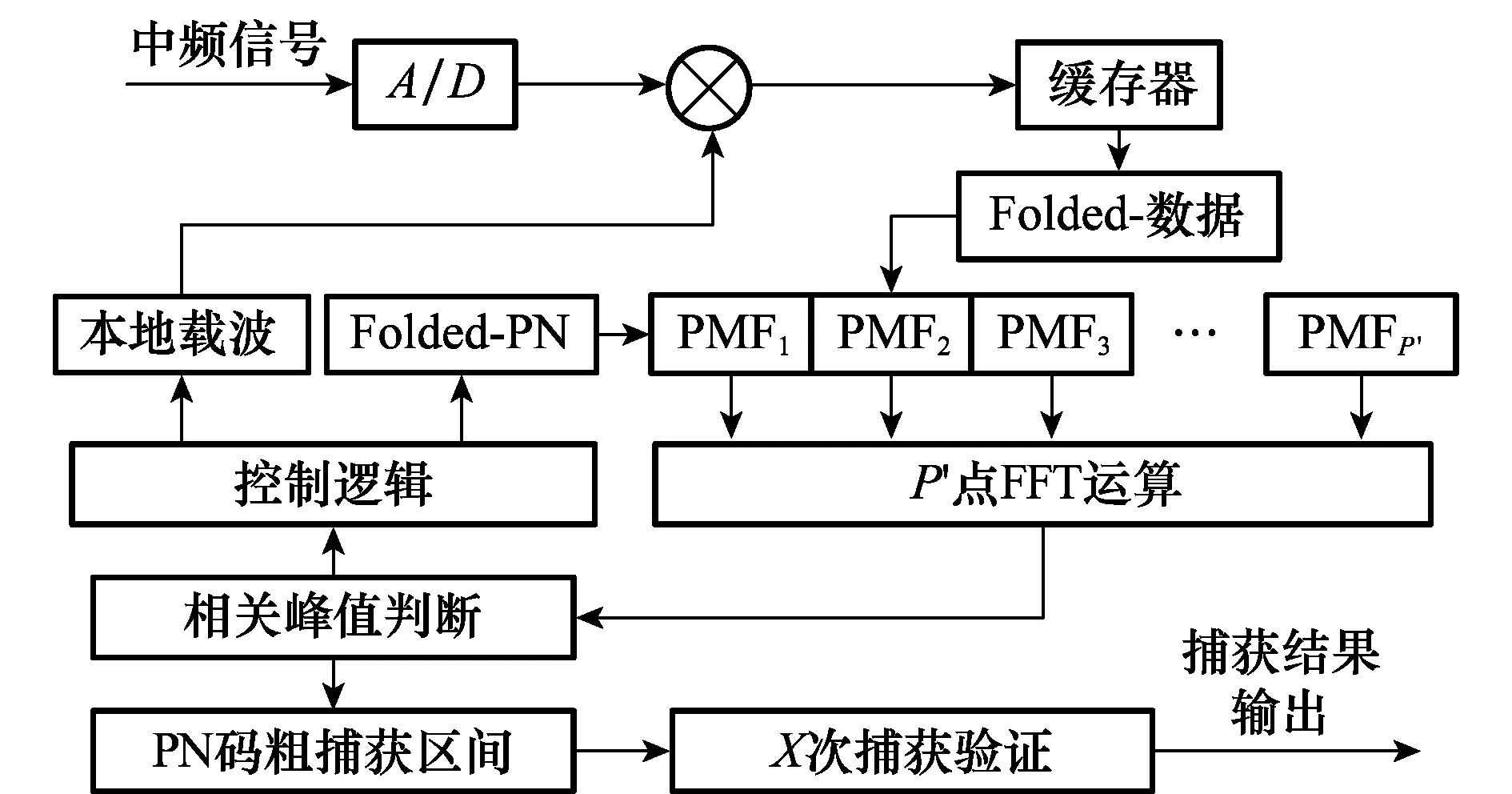
图2 折叠PMF-FFT捕获原理图
如图2所示,缓存器中的信号经过折叠后可表示为
(8)
同样的,折叠后的本地PN码可表示为
(9)
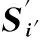
2.1捕获带宽
由于折叠方法对本地PN码和接收数据都作了折叠处理,因此大大缩减了遍历码相位所需的相关运算。如果折叠方法与PMF-FFT方法采用相同的FFT运算点数,那么两种方法的捕获带宽是相同的,此时,折叠方法的计算复杂度远低于PMF-FFT方法。
令折叠方法FFT运算点数为PMF-FFT方法的F倍,即P′=FP,那么由第1.1节中对PMF-FFT方法的捕获带宽分析可知此时的折叠方法的捕获带宽为PMF-FFT方法的F倍。下面对此情况下的折叠方法的计算复杂度作分析。
2.2复杂度分析
由式(8)和式(9)可知,对本地PN码和接收数据作相同长度的折叠处理后,码周期L缩减为L/F,信号累积长度N缩减为N/F,那么遍历码相位所需的相关运算实数乘法和实数加法都减少为NL/F2。与此同时,折叠操作引入的实数加法运算量分别为L/F和N/F;在对PN码粗捕获区间进行F次捕获验证时,按照P点FFT运算的PMF-FFT方法进行验证,此处引入的实数加法和实数乘法运算量分别为F·3P·log2(P)+FN和F·2P·log2(P)+FN。
当折叠方法FFT运算点数为PMF-FFT方法的F倍,即P′=FP时,由第1.2节中对PMF-FFT方法的计算复杂度分析可得到折叠方法完成捕获时所需的实数乘法量和加法量分别为
F·2P·log2(P)+FN
(10)
F·3P·log2(P)+FN+N/F+L/F
(11)
由于式(10)和式(11)包含多个变量,不易直接给出与PMF-FFT方法计算量比较的解析表达式,下面以实际中常用的一组FFT运算点数为例对二者的计算量进行比较。为方便计算令L为128,N为4 096,P分别为32,64,128,256,512,对式(6)、式(7)和式(10)、式(11)的计算量分析如图3所示。
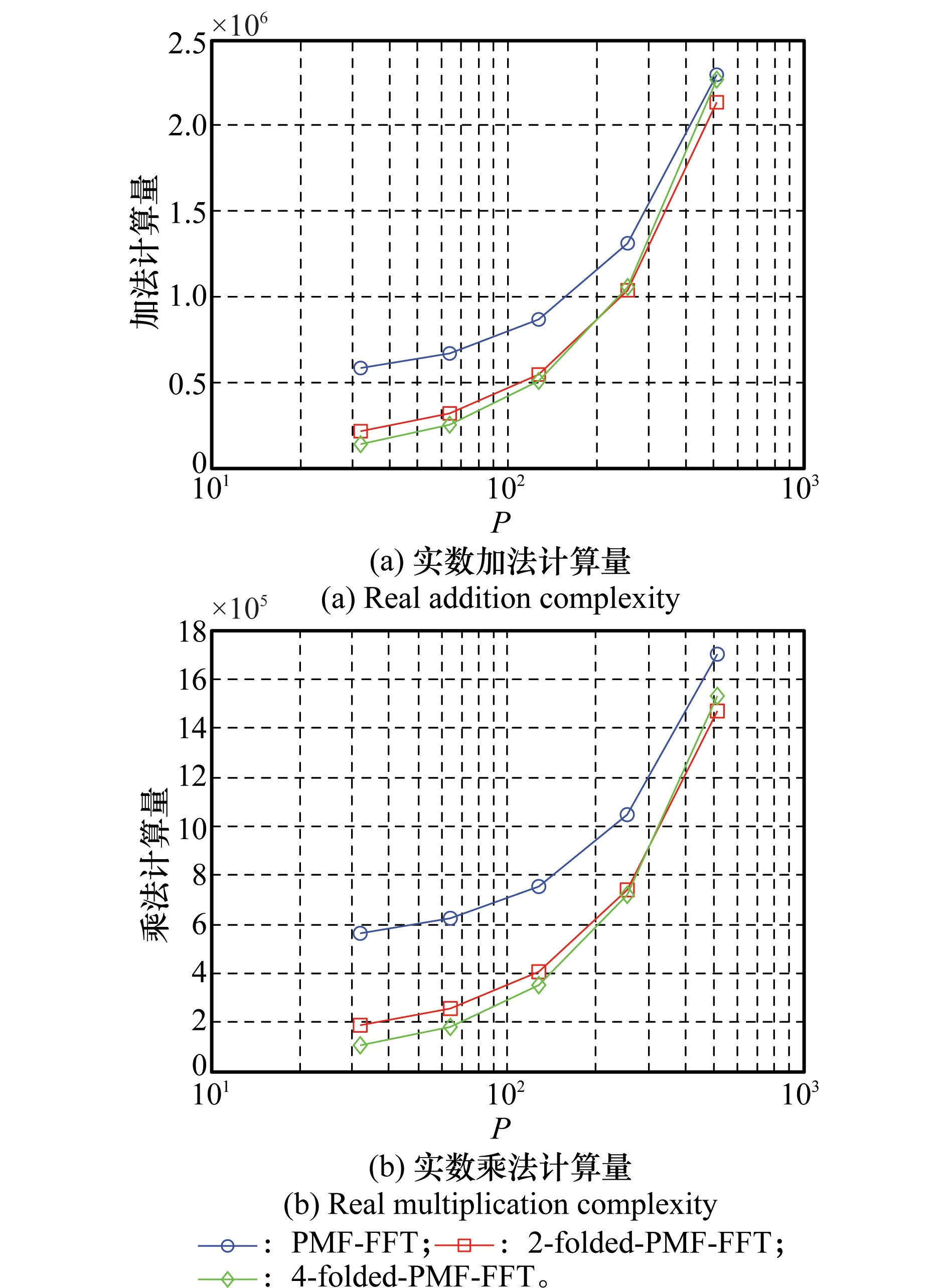
图3 不同方法计算量比较
图3中,2-folded-PMF-FFT表示折叠长度为2的折叠方法,4-folded-PMF-FFT表示折叠长度为4的折叠方法,下文中出现的相同图例均与此含义相同,不再重复说明。从图3可以看到,当PMF-FFT方法的FFT运算点数P<512且折叠方法的FFT运算点数为FP时,以折叠长度为2和4的折叠方法的计算量都小于PMF-FFT方法。当L或N增大时,通过进一步的计算可以发现折叠方法减少的计算量更加明显,而512点的FFT运算在实际工程应用的PMF-FFT方法中已经足够了。
2.3捕获精度和捕获时间
捕获精度包括PN码相位和多普勒频率的捕获精度。在相同的PN码速率、系统采样率和降采样倍数条件下,折叠方法和PMF-FFT方法的PN码捕获精度是相同的;对于多普勒频率捕获精度,在第2.2节的计算复杂度分析中提到折叠方法在进行捕获验证时按照P点FFT运算的PMF-FFT方法进行验证,那么,在系统参数相同的条件下,同样的FFT运算点数所得到的多普勒频率捕获精度是相同的。因此,折叠方法能达到与PMF-FFT方法相同的捕获精度。
平均捕获时间的估算公式[17]为
(12)
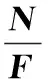
(13)
(14)
式(13)、式(14)中,TP-FFT、TFP-FFT分别表示P、FP点的FFT计算时间。接下来以100 MHz的系统时钟,即Tsys=0.01 us,FFT计算时间以xilinx的v7_1版本的Radix-4型(时延大小适中,资源消耗量适中)计算核为例对两种方法的平均捕获时间进行比较,其余计算参数与第2.2节中相同,比较结果如图4所示。
从图4中可以看到,在PMF-FFT方法的FFT运算点数从32到512时,两种折叠长度的折叠方法平均捕获时间都小于PMF-FFT方法且在部分FFT运算点数条件下,折叠方法的捕获时间只有PMF-FFT的1/4左右。通过进一步的计算分析可以发现,当增大N或L时,折叠方法的平均捕获时间同样小于PMF-FFT方法。折叠方法更短的捕获时间也说明其更加符合高动态环境下对捕获时间的短时延要求。
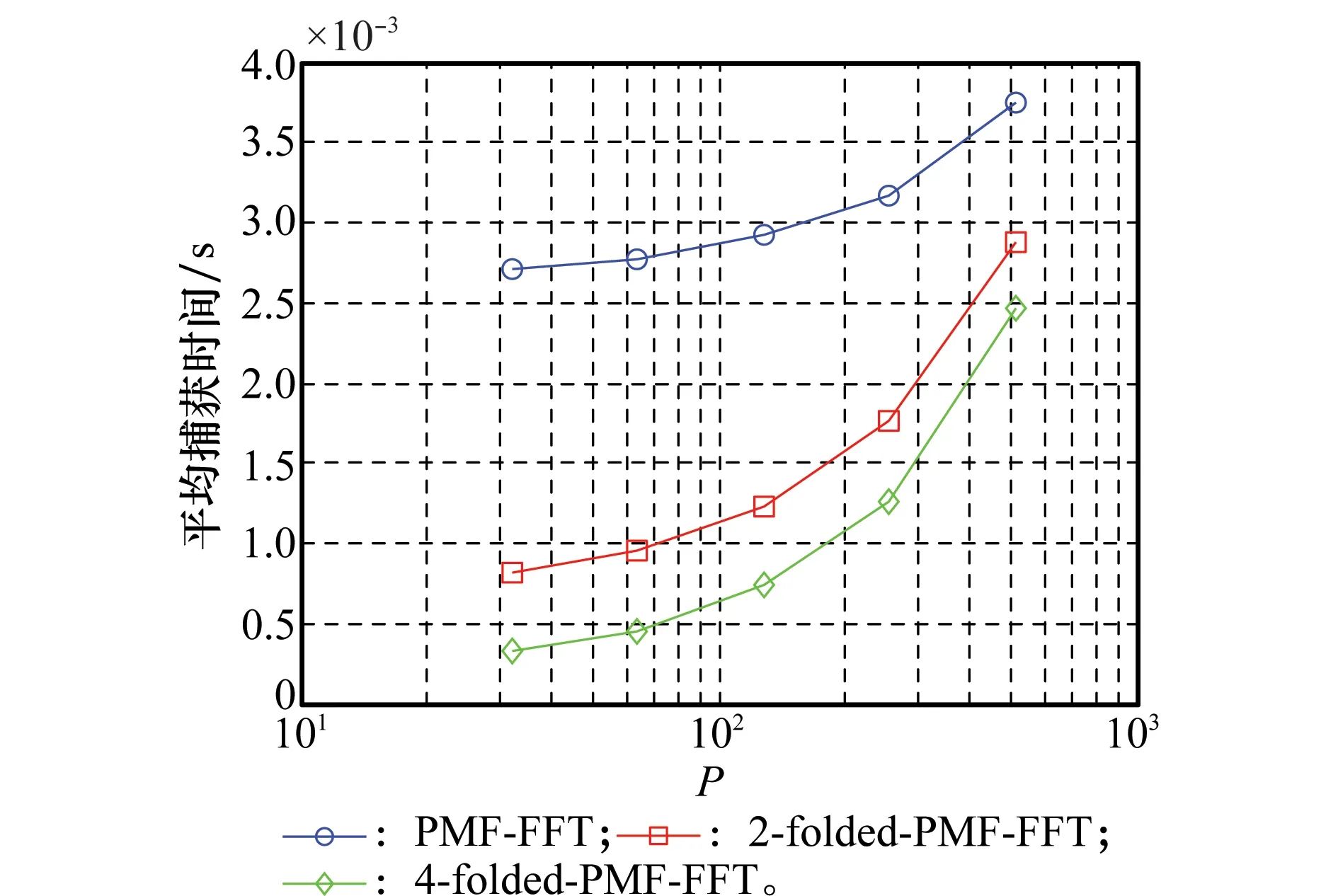
图4 不同方法平均捕获时间比较
2.4频域衰减和扇贝损失
频域衰减和扇贝损失是PMF-FFT捕获方法中不可避免的问题,本文的折叠方法同样存在此问题。当前对频域衰减的改进方法主要为对部分相关之后的数据补零,增加FFT运算点数,从而改善频域衰减;扇贝损失,即FFT的栅栏效应,当前的改进措施主要是对采样数据或部分相关后的数据预先作加窗处理,再进行后续操作,而且不同的窗函数有不同的改善效果[11-13]。对数据补零作FFT的方法本质上是增加了FFT的运算点数,同时也就增加了计算量和硬件资源消耗。
本文提出的折叠方法亦是通过增加FFT运算点数来达到增大捕获带宽的目的,因此,本文的折叠方法本身对频域衰减就起到了改善作用,而且折叠方法在增加FFT运算点数的同时并没有增加总体的计算量和硬件资源。对于扇贝损失,本文提出的折叠方法并没有带来额外的扇贝损失,而且还能结合目前的扇贝损失改进方法进一步提升捕获带宽内的频率捕获精度。
在硬件资源消耗上,尽管折叠方法FFT运算点数高于传统PMF-FFT方法,但是折叠方法缩减了相关运算的时间,可以使用较少的FFT硬核串行计算已完成相关的数据,因此,两种方法的硬件资源消耗是相当的。虽然折叠方法的折叠操作会带来一定的信噪比损失,但是与PMF-FFT方法相比,其捕获带宽能成倍的增加,同时捕获精度与PMF-FFT方法相同,计算复杂度和平均捕获时间都优于PMF-FFT方法。
3 仿真和分析
针对所提出的折叠方法,分别以不同系统参数进行仿真分析,验证其捕获性能,其中,捕获概率以蒙特卡罗仿真1 000次统计得出。文献[8]中的分析计算已将PMF-FFT捕获方法与经典的匹配滤波、PN码循环相关两种PN码并行捕获方法在计算复杂度、捕获时间、硬件复杂度、捕获灵敏度等方面作了比较,并表明PMF-FFT方法性能的优越性和在高动态环境下的实用价值。因此,本文后续的仿真将折叠方法与文献[13]和文献[15]中改进的PMF-FFT方法在捕获时间和捕获性能上作比较。文献[15]对部分匹配滤波的实现结构进行优化,以对PN码进行折叠的方式来优化部分匹配滤波的硬件实现结构,达到减少硬件资源消耗和捕获时间的效果,下文中记此方法为硬件资源优化的PMF-FFT方法(resource optimized PMF-FFT,R-O-PMF-FFT);文献[13]以不同的窗函数对PMF-FFT的数据进行加权改善扇贝损失,以提高捕获精度。其中以第3类Rife-Vincent窗函数的改善效果最佳,下文中记此方法为Rife-Vincent窗函数改进的PMF-FFT方法(Rife-Vincent PMF-FFT,R-V-PMF-FFT)。
3.1捕获精度和捕获时间
R-O-PMF-FFT方法针对匹配滤波问题作了改进,以增加工作时钟频率为代价换取了资源消耗和捕获时间的减少。当码片采样精度为2个点,PN码折叠倍数为4倍的条件下,要求系统的工作时钟频率至少为码片速率的8倍,码片采样精度、折叠倍数、速率更高时,相应的时钟频率也成倍增加。其中,捕获时间的缩短就是以时钟频率的增加达到的,而并不是减少了运算量,同时还带来了高时钟频率系统设计的困难。因此,在相同的时钟频率和资源消耗条件下,该方法与传统的PMF-FFT方法的捕获精度和捕获时间是相同的,即本文的折叠方法在捕获时间上优于R-O-PMF-FFT方法,捕获精度相同。
R-V-PMF-FFT方法以第3类Rife-Vincent窗函数得到了最佳的扇贝损失改善,提高了捕获带宽内的频率识别精度。但是,窗函数的使用对平均捕获时间和捕获带宽并没有带来改善,其捕获时间与传统方法相同,带内捕获精度优于传统方法。因此,通过文中前面小节的分析可以知道,本文折叠方法的捕获时间优于R-V-PMF-FFT方法,在捕获带宽内的频率识别精度低于R-V-PMF-FFT方法。同时,R-V-PMF-FFT方法并没有减少运算量和捕获时间,反而增加了窗函数的运算量。
3.2捕获带宽
下面对不同改进方法的捕获带宽作分析。设定PMF-FFT方法中的P=64,M=N/P=64。由第1.1节的分析可知,在相同的计算复杂度下,R-O-PMF-FFT方法和R-V-PMF-FFT方法的捕获带宽与传统方法的相同,根据式(5)可知此时这两种方法的捕获带宽为15.625 kHz,即±7.8 kHz。分别令折叠方法中的F=2,P′=2P=128和F=4,P′=4P=256,那么折叠方法的计算复杂度是低于PMF-FFT方法的。设定多普勒频偏变化范围为0~36 kHz,信噪比为-10 dB,仿真验证几种方法在不同条件下的捕获带宽如图5所示。
从图5中可以看到,64点FFT运算的R-O-PMF-FFT方法和R-V-PMF-FFT方法在多普勒为8 kHz时,捕获概率降为0;折叠长度为2的折叠方法在多普勒频偏为16 kHz时捕获概率降为0;折叠长度为4的折叠方法在多普勒频偏为32 kHz时捕获概率降为0。此结果验证了折叠方法在对不同多普勒频偏的信号进行捕获时,由于增加了FFT运算点数,其捕获带宽可达PMF-FFT方法的F倍。
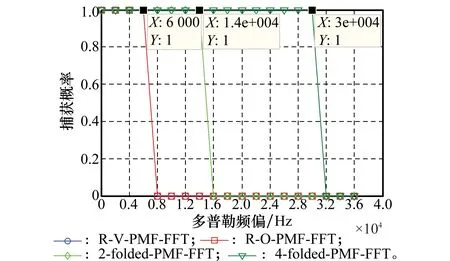
图5 不同方法的捕获带宽
3.3抗噪声性能
此小节对不同方法的抗噪声性能进行比较。仿真参数设置系统采样率为16 MHz,中频载波为4 MHz,二进制相移键控(binary phase shift keying, BPSK)调制,PN码速率1/Tc为1 MHz,伪码周期L为127,下采样倍数为16,信号累积长度N为4 096。按照第3.2小节中设定的仿真条件可以知道,采用64点FFT运算的R-O-PMF-FFT方法和R-V-PMF-FFT方法理论单边捕获带宽为7.8 kHz,2-folded-PMF-FFT方法为15.6 kHz,4-folded-PMF-FFT方法为31.2 kHz。设定多普勒频偏为7.5 kHz,对第3.2小节中的4种方法在不同信噪比情况下进行抗噪声性能仿真,仿真结果如图6所示。
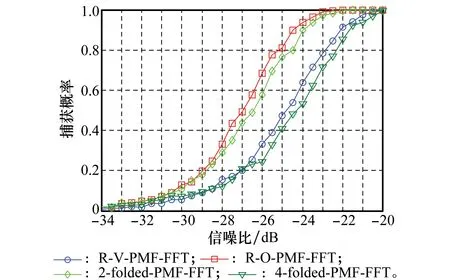
图6 多普勒频偏7.5 kHz,不同方法的捕获性能
由图6可以看到,当多普勒频偏为7.5 kHz时,已接近R-O-PMF-FFT方法和R-V-PMF-FFT方法的最大捕获带宽,而对于不同折叠长度的折叠方法,此多普勒频偏在其正常捕获带宽内。此时,R-O-PMF-FFT方法由于没有其他性能损失,其捕获概率最优;2-folded-PMF-FFT方法由于折叠造成的信噪比损失,其捕获概率略低于R-O-PMF-FFT方法;4-folded-PMF-FFT方法由于折叠造成的信噪比损失增大,其捕获性能与R-O-PMF-FFT方法相差较大;R-V-PMF-FFT方法利用窗函数改善扇贝损失的同时,也增加了FFT频率响应的旁瓣功率,在噪声干扰下,使得捕获概率反而降低。但是,4种方法在信噪比低于-34 dB时,捕获概率接近0;在信噪比高于-20 dB时,捕获性能趋于一致,捕获概率接近1。
设定多普勒频偏为14 kHz,其他仿真参数不变,仿真4种方法的抗噪声性能如图7所示。此时的多普勒频偏值已远超出了R-O-PMF-FFT方法和R-V-PMF-FFT方法的捕获带宽,接近2-folded-PMF-FFT方法的最大捕获带宽。由图7 可以看到,在这种情况下,R-O-PMF-FFT方法和R-V-PMF-FFT方法已完全不能正确捕获,折叠方法仍然能正常工作,而且4-folded-PMF-FFT方法捕获性能优于2-folded-PMF-FFT方法。
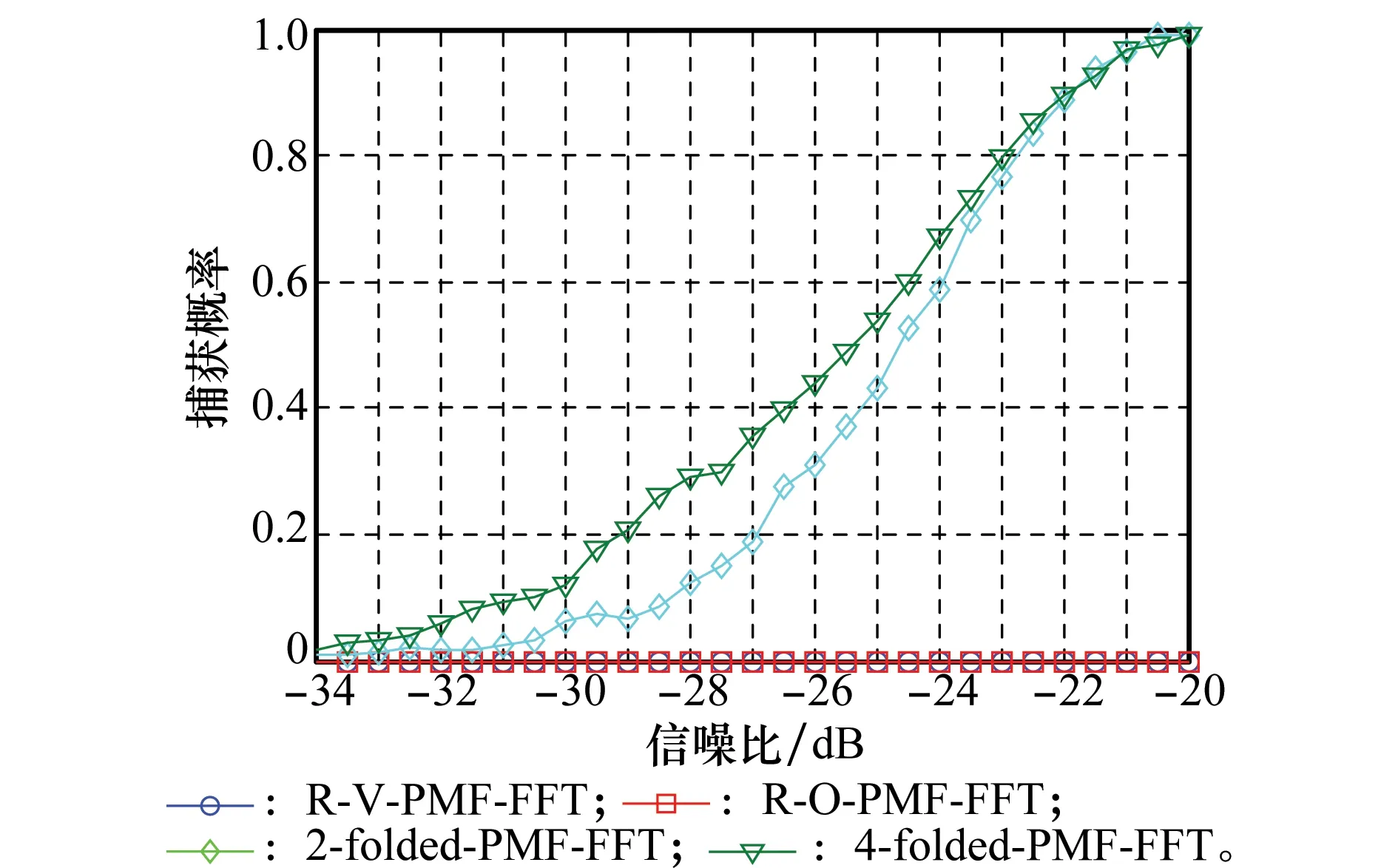
图7 多普勒频偏14 kHz,不同方法的捕获性能
由图6和图7的仿真结果可以看到,改进的折叠方法与R-O-PMF-FFT和R-V-PMF-FFT方法相比,其捕获带宽能达到后者改进方法的F倍。这一结果也验证了第3节中对折叠方法捕获性能分析的正确性。虽然折叠操作会引入信噪比损失,但是在大多普勒频偏情况下,折叠长度较大的折叠PMF-FFT方法的捕获性能也是最优的。同时,在信噪比较大时,不同方法的捕获性能趋于一致,捕获概率都接近于1,即折叠方法在高信噪比时优势更加明显,因为其捕获带宽大,计算复杂度低,捕获速度快,而且与PMF-FFT方法有同的捕获性能。
以上的仿真和分析结果表明,虽然折叠操作会引入一定的信噪比损失,但是在大多普勒频偏情况下,捕获带宽不足的PMF-FFT方法已完全不能正常捕获,而拥有大捕获带宽的折叠方法仍然具有良好的捕获性能。同时,在信噪比较高时,不同方法的捕获性能趋于一致,捕获概率都接近于1,即折叠方法在高信噪比时优势更加明显。不同的仿真参数得到相同的结论也说明折叠方法在一定条件下的普适性。
4 结 论
本文针对传统PMF-FFT方法捕获带宽受限于其FFT运算点数而不能应用于功耗、资源受限的高动态环境的问题,提出折叠PMF-FFT方法。该方法在保持相同捕获精度的条件下,不仅降低了计算复杂度,减少了捕获时间,还成倍的增加了捕获带宽。通过理论和仿真分析验证了折叠方法有效的增加了接收机的捕获带宽,同时捕获时间短,是一种特别适用于高动态环境下直扩信号的快速捕获方法。
[1] Pickholtz R L, Milstein L B, Schilling D L. Spread spectrum for mobile communications[J].IEEETrans.onVehicularTechnology, 1991, 40(2):313-322.
[2] Peterson R L, Ziemer R E, Borth D E.Introductiontospread-spectrumcommunications[M]. New Jersey: Prentice Hall, 1995.
[3] Cheng U, Hurd W J, Statman J. Spread-spectrum code acquisition in the presence of Doppler shift and data modulation[J].IEEETrans.onCommunications, 1990, 38(2):241-250.
[4] Rick R R, Milstein L B. Parallel acquisition in mobile DS-CDMA systems[J].IEEETrans.onCommunications, 1997, 45(11):1466-1476.
[5] Stirling-Gallacher R A, Hulbert A P, Povey G J R. A fast acquisition technique for a direct sequence spread spectrum signal in the presence of a large doppler shift[C]∥Proc.ofthe4thIEEEInternationalSymposiumonSpreadSpectrumTechniquesandApplicationsProceedings, 1996: 156-160.
[6] Liu Y H, Zhao G. Analysis on PMF-FFT based acquisition of PN code[J].CommunicationsTechnology, 2009,42(1):24-26.(刘艳华, 赵刚. 基于 PMF-FFT 的 PN 码捕获方法及性能[J].通信技术, 2009, 42(1):24-26.)
[7] Qi H, Shi X Q, Ji L, et al. The analysis and simulation of PN code acquisition method based on PMF-FFT[J].JournalofXi’anTechnologicalUniversity,2010(1):57-61.(齐华,施小茜,冀乐, 等. PMF-FFT 的 PN 码捕获方法分析及仿真[J].西安工业大学学报, 2010 (1):57-61)
[8] Yuan J G, Ou S L. Study on parallel acquisition algorithm for GPS receiver[J].JournalofChongqingUniversityofPostsandTelecommunications(NaturalScienceEdition),2013,25(4):11-16.(袁建国,欧松林.GPS接收机并行捕获算法的研究[J].重庆邮电大学学报(自然科学版),2013,25(4):11-16).
[9] Ying X, Hong Y. High-sensitivity acquisition of ultrahigh dynamic direct sequence spread spectrum signals in space communications[J].WirelessCommunicationOverZigbeeforAutomotiveInclinationMeasurementChinaCommunications,2013,10(10):26-36.
[10] Feng W Q, Liu X, Li C S. Analysis on acquisition method in spread spectrum TT&C system[J].JournalofBeijingUniversityofAeronauticsandAstronautics,2013,22(7):619-623.(冯文全,刘曦,李春升.扩频测控体制信号捕获方法分析[J].北京航空航天大学学报,2013,22(7):619-623.)
[11] Zhang L Y, Yuan S J, Liu H Y, et al. Research on DSSS signal acquisition algorithm based on windowed PMF-FFT[J].JournalofSystemSimulation,2009,17(11):5536-5539.(章兰英,袁嗣杰,刘海洋,等.基于加窗 PMF-FFT 的扩频信号捕获算法研究[J].系统仿真学报, 2009,17(11):5536-5539.)
[12] Liu N, Sun B, Guan C. Research on an improved PMF-FFT fast PN code acquisition algorithm[J].CommunicationsandNetwork, 2013,5(3):266-270.
[13] Li C J, Yang S X, Ji Z. Performance analysis of fast GPS signal acquisition based on PMF and window FFT[J].JournalofBeijingInstituteofTechnology(EnglishEdition), 2012, 21(3):291-297.
[14] Luo J F, Wang X, Fu Y X, et al. A improved PMF-FFT acquisition for resource-constrained application[J].JournalofComputerResearchandDevelopment,2010,(S2):144-150.(罗炬锋,王翔,付耀先,等.一种针对资源受限应用的改进 PMF-FFT 捕获方法[J].计算机研究与发展, 2010,(S2):144-150.)
[15] Qi J, Luo F, Song Q. Fast acquisition method of navigation receiver based on folded PMF-FFT[C]∥Proc.oftheComputing,CommunicationsandITApplicationsConference(ComComAp), 2014: 62-66.
[16] Li H, Cui X, Lu M, et al. Dual-folding based rapid search method for long PN-code acquisition[J].IEEETrans.onWirelessCommunications, 2008, 7(12):5286-5296.
[17] Lozow J B, Jeff B. Analysis of directP(Y)-code acquisition[J].Navigation, 1997, 44(1):89-98.
Folded PMF-FFT fast acquisition method for high dynamic scenarios
YANG Qin-biao1, WANG Zu-lin1,2, HUANG Qin1, PEI Rui-lin1
(1. School of Electronics and Information Engineering, Beihang University, Beijing 100191, China;2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China)
Due to the big Doppler shift in high dynamic scenarios, it requires extremely large receiver bandwidth to acquire the direct-sequence spread spectrum (DSSS) signal. Nowadays, the partial matching filter-fast Fourier transform (PMF-FFT) acquisition method is widely used for the receiver of the DSSS signal. However, its acquisition bandwidth is limited by FFT points, which brings challenges in high dynamic scenarios. Thus, this paper proposes a low-complexity high-bandwidth folded PMF-FFT method. Firstly, it folds incoming signal, and local pseudo-noise code, as preprocessing. Then, the folded data are processed by the PMF-FFT method. Theoretical analysis and numerical results demonstrate the proposed method withFfolding times is able to achieve F times bandwidth of that of PMF-FFT. Moreover, it costs even less computational complexity.
high dynamic; direct-sequence spread spectrum (DSSS); partial matching filter-fast Fourier transform (PMF-FFT); folded
2015-10-19;
2016-02-19;网络优先出版日期:2016-04-15。
国家自然科学基金(61471022)资助课题
TN 911
A
10.3969/j.issn.1001-506X.2016.08.03
杨秦彪(1986-),男,博士研究生,主要研究方向为无线通信系统和信号处理。
E-mail:yangqinbiao@yahoo.com
王祖林(1965-),男,教授,博士,主要研究方向为现代通信中信号处理、甚小孔径卫星通信的理论与技术、电子与信息对抗的理论与技术。
E-mail:wzulin@vip.sina.com
黄勤(1986-),男,副教授,博士,主要研究方向为无线通信、信道编码。
E-mail:qinhuang@buaa.edu.cn
裴睿淋(1985-),女,博士研究生,主要研究方向为无线通信系统和信号处理。
E-mail:peirlee@163.com
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160415.1126.006.html

