基于二体模型的空间目标双基地ISAR回波模拟

郭宝锋, 尚朝轩, 王俊岭, 高梅国

(1.军械工程学院电子与光学工程系, 河北 石家庄 050003;2. 北京理工大学信息与电子学院, 北京 100081)



基于二体模型的空间目标双基地ISAR回波模拟

郭宝锋1,2, 尚朝轩1, 王俊岭2, 高梅国2

(1.军械工程学院电子与光学工程系, 河北 石家庄 050003;2. 北京理工大学信息与电子学院, 北京 100081)

针对空间三轴稳定目标成像问题,提出了一种基于二体模型的双基地逆合成孔径雷达(bistatic inverse synthetic aperture radar,ISAR)回波模拟方法。该方法利用二体运动模型模拟空间目标的在轨运动,考虑了目标平稳运动及三轴姿稳转动引起的散射点相对雷达视角变化,并加入目标的高速运动特性,生成了双基地逆合成孔径雷达的基带回波数据,并给出了双站雷达对目标可视区域的判定方法。最后,进行了仿真实验,仿真结果表明,二体模型与实际目标的运动轨道误差很小,同时,成像结果能够很好的反映目标的姿态变化特性。该回波模拟方法有利于空间目标的精确成像,并对成像试验的实施具有重要的指导意义。

双基地逆合成孔径雷达; 二体模型; 空间目标; 回波模拟

0　引　言

双基地雷达是发射机和接收机分置、且基线长度与目标距离可比拟的雷达系统,收发分置的工作方式使雷达在对抗“四大威胁”方面具有突出的优势[1]。双基地逆合成孔径雷达是基于双基地雷达平台的逆合成孔径雷达(inverse synthetic aperture radar, ISAR) 系统,在具备“四抗”特性的同时,它利用接收的目标非后向散射回波进行成像,能够较单基地雷达获取更加丰富的目标信息[2-3],双(多)基地雷达系统日益成为现代雷达研究的热点问题[4-7]。同时,随着雷达成像和空间技术的发展,对成像目标的选取不再限于地面、海面以及空中目标,对空间目标的探测、成像及识别已成为一个前沿课题[8-9]。

目前,对双基地ISAR成像的研究以理论为主,主要集中在成像原理、分辨率、成像平面以及成像算法等问题[5,10-13]的研究上,对这些理论的仿真验证所使用的模拟回波数据大都基于收发双站雷达与目标运动轨迹共面的假设下产生的,且只考虑了目标平动引起的视角变化。而实际上,收发双站雷达在绝大多数情况下与目标运动轨迹不共面,并且不同的空间目标还会具有不同的旋转特性,这使得传统的回波模拟方法难以反映目标各散射点与雷达之间的相对运动,也无法由此验证所采用成像算法的实际成像效果。文献[14]对轨道飞行目标的雷达回波进行模拟和成像仿真,重点探讨了轨道飞行目标成像对雷达重复频率和相干积累时间的要求,该文献没有考虑目标实际姿态与雷达视线的关系,认为目标轨迹与雷达始终共面,且没有考虑目标在轨运动的高速运动特性和目标自转特性;文献[15]利用空间目标的运动特性,给出了弹道目标轨道方程的计算方法,并重点分析了导弹弹道高速运动对回波信号的影响,该文献侧重于弹道的研究,没有考虑目标姿稳转动对成像的影响。然而,目标绕自身旋转轴的转动一方面会影响目标的累积转角计算,进而影响目标的方位尺寸定标及后续的目标识别,另一方面会影响成像平面的确定和成像分析,在实际空间目标成像时,目标自旋对成像的影响不可忽视。

本文根据空间目标的轨道运动特性,提出了一种基于二体模型的双基地ISAR回波模拟方法。该方法在三维空间建立散射点模型,利用两行轨道根数(two line elements, TLE)计算目标的运动轨迹,并考虑目标的高速运动特性和对地姿稳转动,模拟生成了基带回波数据并进行了成像仿真。

1　空间目标的运动特性建模

空间三轴稳定目标的运动由目标的在轨平稳运动和绕质心的转动叠加而成,而目标的平稳运动可通过质心的运动描述。根据TLE根数可以确定目标质心在地心观测坐标系下的坐标及其与地心赤道坐标系的转换关系,目标上各散射点在当前时刻地心观测坐标系下的坐标是恒定的,而收发双站雷达的位置是在地固坐标系下确定的,为了得到散射点相对收发双站的距离,需要将散射点坐标和雷达坐标转换到同一坐标系下。文中首先将散射点在地心观测坐标系下的坐标转换到地心赤道坐标系下,而后转换到雷达位置所在的地固坐标系下,这样,通过散射点与雷达的坐标即可精确计算各个时刻散射点相对双站雷达的距离。

1.1坐标系统的定义及坐标转换

文中用到多个空间坐标系统,并涉及相互转换关系,对将要涉及的坐标系统和旋转矩阵进行定义。

对空间坐标系统的定义[16]如下:

(1)地心赤道坐标系XYZ:又称地惯坐标系,以地心为原点O,X轴指向春分点的方向,Y轴在赤道平面内向东90°,Z轴与地轴平行指向北极点,与X轴、Y轴共同组成右手坐标系。

(2)地心地固坐标系X′Y′Z′:又称地固坐标系,以地心为原点O′,X′轴指向本初子午线与赤道的交点,Y′指向东经90°与赤道的交点,Z′轴与地轴平行指向北极点。该坐标系随地球的自转而转动。

(3)地心观测坐标系xyz:以地心为原点o,x轴由地心一直指向卫星,y轴在轨道平面内与x轴垂直,并指向卫星运动方向,z轴与x轴、y轴共同组成右手坐标系。

(4)星基观测坐标系x′y′z′:该坐标系由初始观测时刻t0的卫星位置决定,以卫星质心为原点o′,由地心指向卫星的矢量为x′轴,y′轴在卫星的轨道平面内,与x′轴垂直,正方向为卫星运动方向,z′轴与x′轴，y′轴组成右手坐标系。该坐标系三轴指向不变化,原点随目标中心变化。

对坐标系旋转矩阵的定义如下:

在右手坐标系XYZ中,绕X轴正转的表达式为

(1)

绕Y轴正转的表达式为

(2)

绕Z轴正转的表达式为

(3)

其中,正方向的定义为:绕X轴旋转,从X轴正端向原点看,Y轴沿逆时针方向旋转向Z轴;绕Y轴旋转,从Y轴正端向原点看,Z轴沿逆时针方向旋转向X轴;绕Z轴旋转,从Z轴正端向原点看,X轴沿逆时针方向旋转向Y轴。

1.2目标质心的运动

若将地球看成一个密度分布均匀的球体,则它对绕其运行的空间目标的引力作用等效于一个质点,相当于质量全部集中在质心上,于是构成了一个简单的二体运动,如图1所示。

图1　卫星轨道模型[16]

在二体运动假设下,卫星的轨道方程[16]为

(4)

轨道方程(4)由3个相互独立的参数h，e以及f决定,描述了空间目标在轨道平面内的圆锥曲线运动。实际运算过程中,角动量h和真近点角f常用半长轴a和平近点角M代替。为获得三维空间内空间目标轨道的方位,还需要另外3个附加参数,即欧拉角,分别为为升交点赤经Ω、轨道倾角i、近地点幅角ω。由空间目标的轨道六根数(a, M, i, ω, e, Ω)便可确定二体运动下空间目标的轨道。

由于考虑的目标为二体运动,卫星旋转中心在地心观测坐标系xyz的坐标可表示为

(5)

式中,r为地心到卫星旋转中心的距离,可由式(4)得到。

令雷达对卫星初始观测时刻卫星的轨道根数为χt0=(a, Mt0, i, ω, e, Ω),忽略岁差和章动在观测时间段内对天极和春分点的影响,则在初始观测时刻,由地心观测坐标系xyz转到地心赤道坐标系XYZ需要首先绕z轴顺时针(逆旋)旋转ft0+ω,然后绕x轴顺时针(逆旋)旋转i,最后绕z轴顺时针(逆旋)旋转Ω。其中,ft0为初始观测时刻卫星的真近点角,该值可根据卫星的初始轨道根数求得。

由于二体运动假设,除了平近点角外,其余轨道根数均保持不变。而平近点角可由以下公式计算获得

(6)

式中,tepoch为初始轨道根数历元时刻;t0为初始观测时刻的历元。

而在同一观测的任意后续的观测时刻t,由地心观测坐标系xyz转到地心赤道坐标系XYZ需要的坐标系旋转与初始时刻不同之处在于先绕z轴的顺时针(逆旋)旋转角不是ft0+ω而是ft+ω。其中,ft为t时刻卫星的真近点角。由地心观测坐标系xyz的定义可知后续的坐标系旋转与初始观测时刻所需做的旋转相同。

因此,任意观测时刻t,由地心观测坐标系xyz转到地心赤道坐标系XYZ所做的坐标旋转矩阵为

(7)

式中,Rx(·)以及Rz(·)分别表示右手坐标系绕x轴和z轴的旋转矩阵。

在不考虑极移的情况下,地心赤道坐标系XYZ与地固坐标系X′Y′Z′之间的差别是地球自转角—格林尼治恒星时[17]SG,由坐标系XYZ转换到X′Y′Z′需逆时针旋转相应的自转角度,对应的旋转矩阵可表示为

(8)

式中,SGt0为在初始观测时刻t0的地球自转角—格林尼治恒星时;nE为地球自转角速度,该值为86 164.098 903 691s。

格林尼治恒星时的计算公式为

SG=18h.697 374 6+879 000h.051 336 7 tJ+

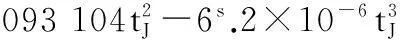
(9)

式中,tJ可表示为

(10)

式中,JD(t)为观测时刻t的儒略日;JD(J2 000.0)是历元J2 000.0对应的儒略日。

令雷达所在位置的经度、纬度和海拔分别为θLong、θLat和hR,则雷达在地固坐标系X′Y′Z′的坐标矢量可表示为

(11)

式中,假设地球为标准球形,RE为地球半径,一般为6 378.15km。

由式(5)～式(11)可得在地固坐标系X′Y′Z′雷达对卫星的观测矢量为

(12)

1.3目标的姿稳转动

(13)

式中,θz′为观测时刻t相对时刻t0目标绕z′轴的转动角度；Rz(-θz′)为绕z′轴的旋转矩阵,由于目标逆时针转动,即相当于坐标系顺时针旋转,故为负值。

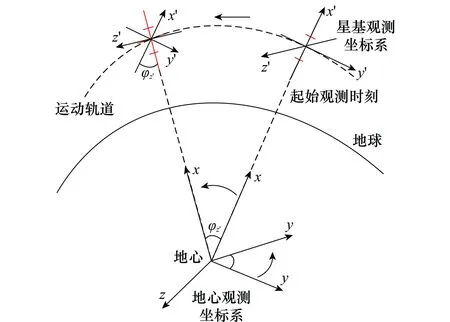
图2　三轴姿稳目标运动模型

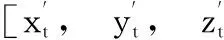
(14)

对地三轴稳定卫星,由于其姿态对地心保持不变,卫星自旋转角与卫星的真近点角变化一致,因此卫星的自旋转角变化率也与卫星的真近点角变化率一致。故有

(15)

将式(15)代入式(14)可得

(16)

即,对地三轴稳定卫星在轨运行时的姿态调整使得卫星各散射点在任意观测时刻t的地心观测坐标系xyz中保持不变,旋转矩阵Rz(φz′)与Rz(-θz′)进行了抵消。

由于卫星在轨运行时期真近点角f的变化率满足以下等式

(17)

式中,h为卫星每单位质量的角动量;e≥0为轨道偏心率;n为卫星的平均角速度。

因此,对具有一定偏心率的卫星,卫星的自旋转角的变化率可表示为

(18)

可见,对非零偏心率轨道的目标,目标在轨道不同的位置上有不同的自旋角速度,对ISAR成像的影响也不同。

1.4质心运动与姿稳转动的叠加

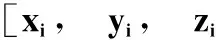
(19)

式中,Cα与Sα分别为角度α的余弦和正弦值;α=-ft-ω;β=-i;γ=-(-SGt0-nEt+Ω)。

则雷达与卫星各散射点之间的距离可表示为

(20)

径向速度可通过对rDis进行求导获得,即

(21)

式(19)、式(20)可得到任意时刻任意散射点与雷达站的位置矢量及速度参数,对式(21)求二阶导即可得到加速度参数。

1.5双站雷达对目标可视区域的判定

实际空间目标探测时,雷达可以看到目标的圈次有限,并且每个圈次的观测时间也很有限,收发双站雷达能同时看到目标的机会更少,目标的不可视区域对成像是没有意义的,因此,下面通过双站雷达与目标的几何关系来确定目标对雷达的可视区域。

目标可视区域确定示意图如图3所示,不考虑雷达的探测距离,雷达的可视部分是雷达所在地平线以上区域,从图中可以看出,区域1和区域3是发射站雷达的可视区域,区域2和区域3是接收站可视区域,区域3是收发双站雷达的公共可视部分。设发射站、接收站到目标的矢量分别为TS、RS,地心到发射站、接收站的矢量分别为TE、RE,地球可近似为球体,则发射站看到目标时,矢量TS和TE的夹角φT为锐角,即需满足TS和TE的矢量积大于0,同理,接收站能够看到目标时,RS和RE的矢量积也要大于0,据此可以确定双站看到目标的区域应满足

(22)

图3　目标可视区域确定示意图

2　脉内多普勒调制及回波信号生成

空间目标为高速运动目标,当雷达发射信号的时宽带宽积较大时,速度对脉内多普勒的调制不可忽略,在回波信号生成时需要加入脉内多普勒的调制信息。

假设发射站和接收站有理想的时间同步,发射站雷达以脉冲重复时间(pulserecurrencetime,PRT)发射线性调频信号

(23)

设目标上某散射点Pi的散射系数为ρi,并假设散射点在目标运动过程中雷达截面积(radarcrosssection,RCS)恒定。tm时刻,散射点Pi到发射站和接收站雷达的距离分别为RTpm和RRpm,由于脉冲持续期间,目标转动引起的速度很小,可认为目标上任意散射点到雷达的径向速度是一样的。tm时刻,设目标相对发射站和接收站雷达的径向速度分别为vTm和vRm(目标远离雷达为正,靠近为负),则散射点Pi到收发双站的距离、径向速度分别为

(24)

(25)

(26)

(27)

式(26)和式(27)的近似忽略了脉冲在收发期间加速度对目标各散射点位置的影响。对距离发射站1 500Km的空间目标,延迟τ1为5ms,此期间(指波形离开发射站到碰到目标期间),假设目标的加速度为100m/s2,由此产生的目标位置变化为0.125mm,对于波长3cm的回波数据,目标位置变化会使回波中的所有数据相位都增加或减少1.5°,由于成像期间目标的距离及加速度变化是平缓的,其他各次回波的相位也会变化1.5°左右,该变化量很小,又是规律的,不会对成像有影响。若发射信号脉宽为1ms,在脉冲期间,由加速度引起的目标位置变化约为5×10-5m,位置变化会使回波数据的相位发生不均匀的变化,但由于该距离变化量为波长的1/600,对回波数据的相位影响也可忽略。因此,进行回波模拟时,目标匀速运动的假设是合理的。

由式(26)和式(27)可得脉冲点从发射站雷达到达接收站雷达的总延迟时间τ为

(28)

“停-走”模型中,认为脉内的目标静止,相应的时间延迟是固定的,对于高速运动目标,不同发射时刻,回波时间延迟是变化的,致使脉内产生多普勒的变化。

经时间延迟后,接收站雷达接收到回波的绝对时刻t为

(29)

由于回波采样的绝对时刻t是已知的,结合式(28)和式(29),可得延迟时间τ与回波接收时刻t的关系,并整理可得

(30)

将雷达发射信号式(23)的时间延迟τ,与本振混频后下变频至中频,即可得到基带回波信号

(31)

散射点的距离、速度等信息均可由二体运动模型得到。

3　回波模拟流程

双基地ISAR基带回波数据模拟的基本流程如图4所示。具体步骤如下:

步骤 1设置初始参数,包括发射信号载波频率fc、脉冲宽度Tp、脉冲重复周期PRT、信号带宽B、调频率K=B/Tp,以及快时间采样率fs等;

步骤 2设置散射点模型,即目标的各散射点在星基坐标系下的三维坐标和散射系数;

步骤 3计算脉冲发射0时刻散射点的轨道位置,并将其转换到地固坐标系下,并根据雷达双站的位置,计算散射点到发射站、接收站及双站的距离和速度,并根据式(30)确定快时间采样对应的时间延迟,再根据式(31)得到各采样时刻的回波数据;

步骤 4对新的散射点,重复步骤3,直至完成所有散射点的单次回波数据的采样;

步骤 5对下一个回波脉冲,重复步骤3、步骤4,直至完成成像所需脉冲个数的回波模拟生成。

得到目标的模拟回波之后,就可以根据距离-多普勒(range-Doppler,RD)成像算法进行成像仿真。

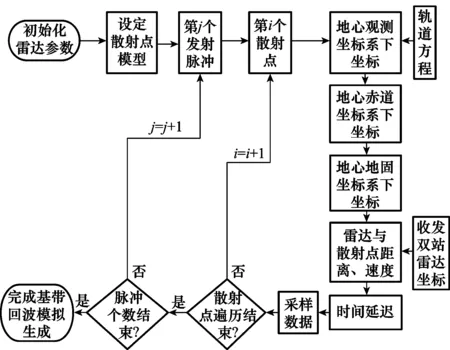
图4　基带回波信号模拟流程

4　仿真实验及结果分析

本节采用国际空间站的轨道根数进行仿真,首先验证二体模型产生轨道的准确度,然后通过成像实验说明回波模拟过程的正确性。

4.1二体运动模型轨道仿真实验

为验证基于二体运动模型轨道外推方法的正确性,设置发射站、接收站分别位于于A城市、B城市,所采用的轨道为由Space-track公布的国际空间站在2012年12月31日的TLE根数:

125544U 98067A 12366.89848378.0000671500000-011734-3 09373

225544 051.6460 219.3718 0016515 109.6991 015.4155 15.51833175808723

由TLE根数可知历元初始时刻为2012年12月31日21:33:48.96。

由于真实的目标运动轨迹未知,这里可采用美国航天司令部开发的SGP4模型对轨道进行预报,SGP4模型是一种摄动模型,该模型考虑了日月引力项和地球引力摄动的影响,较二体模型精确,但是SGP4模型只能用于描述散射质心在空间的运动轨迹,它是一个非解析过程,不能描述目标上质心以外的散射点的运动状态,并且,空间目标大都是三轴稳定目标,用SGP4模型无法反映目标上散射点在运动轨道内的姿稳转动特性,即不能使用SGP4模型产生目标散射点的回波。将SGP4模型产生的轨道数据作为参照数据,与本文的二体运动轨道数据进行对比,可以反映二体运动模型的准确程度。

二体运动模型与SGP4模型的仿真结果对比如图5(a)～图5(d)所示,仿真时间为从历元时刻外推20 000 s,其中图5(a)为二体运动产生的地心到卫星的距离变化规律,从距离曲线上可以看出,卫星绕地球做椭圆运动,在仿真的近4个运行周期内,其近地点与远地点到地心的距离是恒定的,这与卫星绕地运行的规律相一致。图5(b)～图5(d)分别为二体运动模型与SGP4模型得到的发射站、接收站以及收发双站到卫星的距离,两种模型得到的距离曲线基本重合,说明了二体运动轨道模型能够反映卫星在空间的运动特性。

图5　二体运动模型与SGP4模型随外推时刻的距离变化

图6给出了二体运动模型与SGP4模型的距离绝对误差及其相对误差,图6(a)可以看出,二体运动模型与SGP4模型的轨道误差很小,距离的绝对误差在10 km量级,该误差主要是由二体运动模型与SGP4模型之间模型差异引入,同时,距离误差是周期震荡的,其幅度随着外推时间的增加而变大,这主要是由于二体运动模型中忽略了轨道根数的长期项而引入的。图6(b)以SGP4模型的距离作为参考,给出了相对误差,在相对初始历元时刻的2 h内,其相对误差不到1%,在相对初始历元的4 h内,其相对误差不超过2.5%,随着时间的外推,相对误差也是周期变化趋势且峰值是变大的。

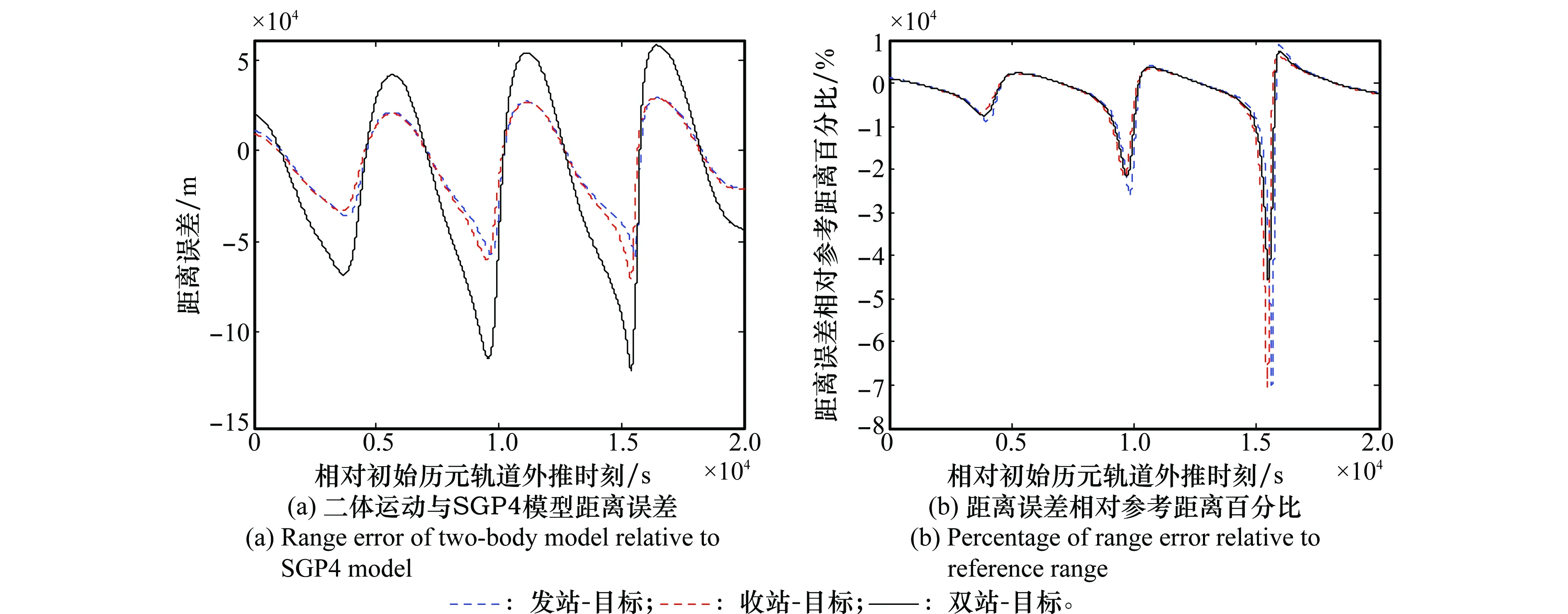
图6　二体运动与SGP4模型距离误差及其相对参考距离百分比

从仿真情况来看,二体运动轨道模型是存在误差的,但相对空间目标来说,该误差比例很小,完全能够反映卫星的运动特性,由于建立轨道模型的目的在于仿真分析卫星在轨运行以及接近收发站的特点并进行成像,而非获得任意时刻的精确卫星轨道值,因此,采用该模型计算卫星轨道是可行的。

4.2空间目标双基地ISAR成像仿真实验

为验证回波数据的正确性,进行了双基地ISAR的成像仿真,收发双站位置及TLE轨道采用第5.1节的参数。根据1.5节给出的目标可视区域判定方法,可以计算得到双站雷达对目标的某个可视圈次的可视时间范围为2013年1月1日01:49:56～01:56:49,即总共413 s。这里选择3个成像弧段进行成像,弧段之间的时间间隔均为100s,这3个弧段分别为:

弧段1:01:51:42～01:51:52.22

弧段2:01:53:22～01:53:32.22

弧段3:01:55:02～01:55:12.22

仿真场景及成像段如图7所示,散射点模型如图8所示,该模型是由307个散射点组成的复杂结构。仿真雷达参数及成像参数如表1和表2所示。

表1　仿真雷达参数

采用本文方法产生目标模拟回波后,首先通过速度补偿[18]消除高速运动对脉内多普勒的影响,而后采用经典的RD成像算法对回波数据进行成像,3个成像弧段的成像结果如图9所示。

图7　仿真场景及所选成像段

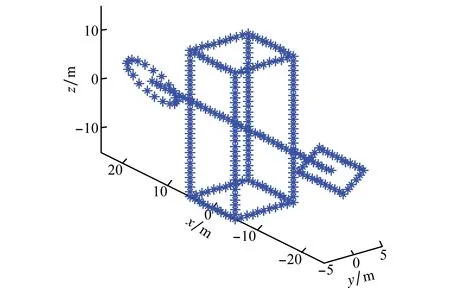
图8　散射点模型及其俯视图

对比图9中3个弧段的成像结果,不同的成像段成像结果是不同的,但都恢复出了目标的形状特性,说明了本文基带回波模拟方案的正确性。同时,3个成像段的成像结果也反映了成像期间目标相对雷达的姿态变化,实际空间目标成像时也是这样,不同的成像弧段对应着不同的目标姿态,这也进一步表明,本文基于二体运动模型的空间目标双基地ISAR回波模拟的正确性。

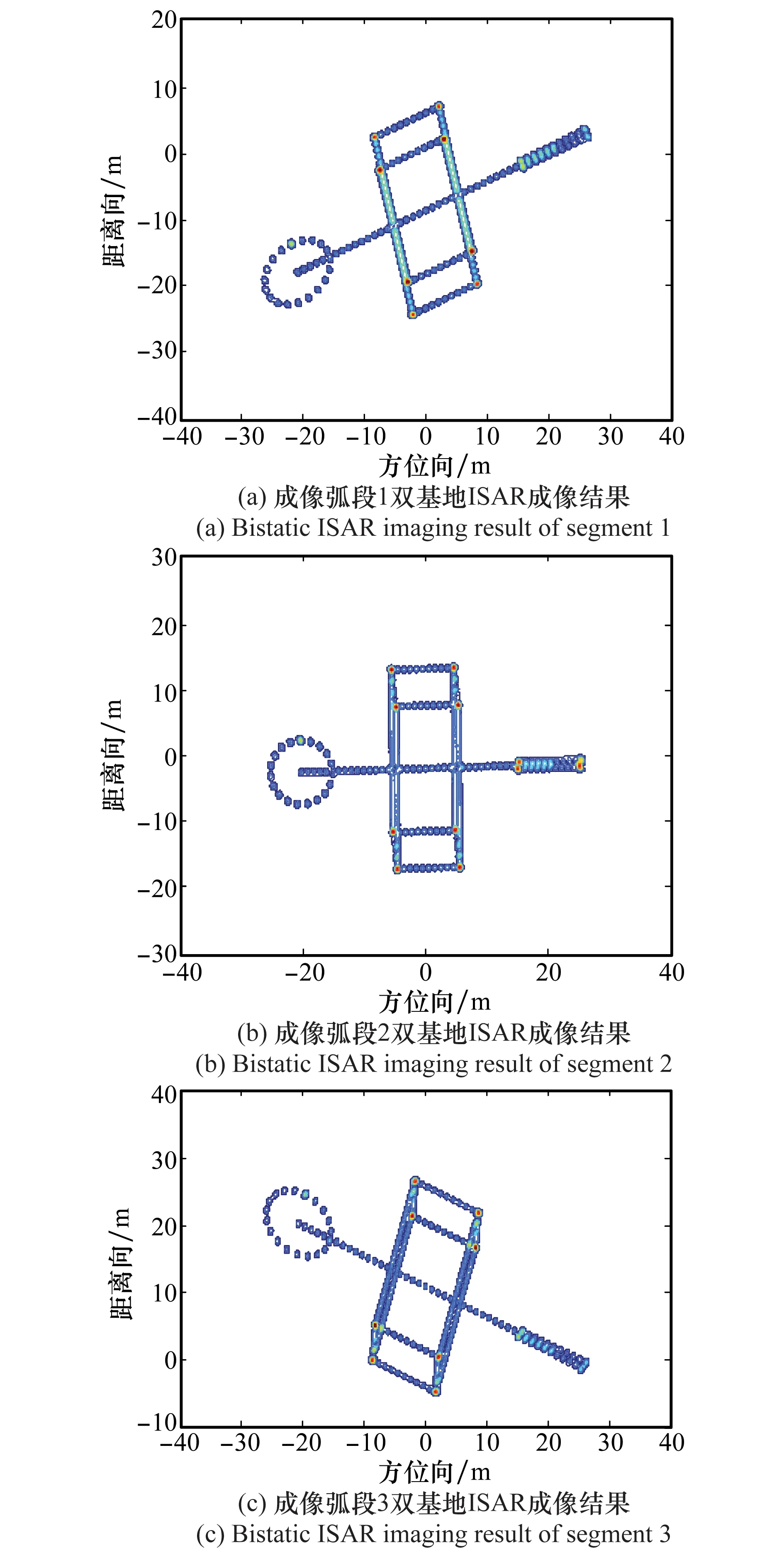
图9　3个成像弧段双基地ISAR成像结果

参数名称参数值成像段1成像段2成像段3累积脉冲个数/个512512512包络对齐累积互相关累积互相关累积互相关相位校正多特显点多特显点多特显点平均双基地角/(°)57.474.251.6累积转角/(°)2.572.703.2距离分辨率/m0.4280.4700.417方位分辨率/m0.3810.4000.298

5　结　论

本文针对空间目标成像,研究了双基地ISAR的回波数据生成方法,并完成了成像仿真。首先基于二体运动模型,利用TLE轨道根数,模拟生成空间目标质心的运行轨道;其次,建立了散射点的三维空间模型,并考虑目标的高速运动和姿稳转动,生成了双基地ISAR的回波数据;最后,分别对模拟的轨道和回波数据进行了仿真验证。结果表明,基于二体模型的轨道与实际轨道高度吻合,回波数据成像结果能够充分反映目标的姿态特性,对成像试验的实施具有重要的指导意义。本文提出的回波建模方法紧密结合空间三轴稳定目标实际,但未考虑散射点的闪烁特性和遮挡效应,这种复杂情况下的成像仿真仍需进一步研究。

[1] Yang Z Q, Zhang Y S, Luo Y J.Bistatic(Multistatic)radarsystem[M].Beijing: Defense Industry Press,1998:14-15.(杨振起,张永顺,骆永军.双(多)基地雷达系统[M].北京:国防工业出版社,1998:14-15.)

[2] Ma C Z, Tat S Y, Guo Q, et al. Bistatis ISAR imaging incorporating interferometric 3-D imaging technique[J].IEEETrans.onGeoscienceandRemoteSensing, 2012, 50(10): 3859-3867.

[3] Peng S B, Xu J, Meng C Z, et al. LFMCW bistatic ISAR space target velocity compensation based on IPD method[C]∥Proc.oftheIETInternationalRadarConference, 2013:1-4.

[4] Bai X R, Zhou F, Xing M D, et al. Scaling the 3-D image of spinning space debris via bistatic inverse synthetic aperture radar[J].IEEETrans.onGeoscienceandRemoteSensingLetters,2010,7(3):430-434.

[5] Comblet F, Khenchaf A, Baussard A, et al. Bistatic synthetic aperture radar imaging: theory, simulation, and validation[J].IEEETrans.onAntennasandPropagation,2006,54(11):3529-3540.

[6] Gustavsson A, Ulander L M H, Flood B, et al. Low frequency bistatic SAR measurements[C]∥Proc.oftheIEEEInternationalGeoscienceandRemoteSensingSymposium, 2012: 315-318.

[7] Pan X Y, Wang W, Feng D J, et al. On deception jamming for countering bistatic ISAR based on sub-Nyquist sampling[J].IETRadar,SonarandNavigation, 2014, 8(3): 173-179.

[8] Bai X R, Zhou F, Bao Z. High-resolution radar imaging of space targets based on HRRP series[J].IEEETrans.onGeoscienceandRemoteSensing, 2014, 52(5): 2369-2381.

[9] Fu X J, Zhao L Z, Zhao H P, et al. Bi-static inverse synthetic aperture radar imaging for space objects[C]∥Proc.ofthe5thInternationalCongressonImageandSignalProcessing, 2012: 1774-1777.

[10] Zhu X P, Zhang Q, Zhu R F, et al. Study on correction algorithm of migration through resolution cell in bistatic ISAR[J].SystemsEngineeringandElectronics,2010,32(9):1828-1832.(朱小鹏,张群,朱仁飞,等.双站ISAR越距离单元徙动分析与校正算法[J].系统工程与电子技术,2010,32(9):1828-1832.)

[11] Martorella M, Palmer J, Homer J, et al. On bistatic synthetic aperture radar[J].IEEETrans.onAerospaceandElectronicSystems, 2007, 43(3): 1125-1134.

[12] Martorella M, Cataldo D, Brisken S. Bistatically equivalent monostatic approximation for bistatic ISAR[C]∥Proc.oftheIEEERadarConference, 2013：1-5.

[13] Dong J, Gao M G, Shang C X, et al. Research on image plane of bistatic ISAR[C]∥Proc.oftheIETInternationalRadarConference, 2009：1-6.

[14] Zhang J Y, Zhang Q W. ISAR echo simulation and imaging of the target in orbit[J].ActaElectronicSinica, 1995, 23(9): 28-31. (张剑云,张庆文. 轨道飞行目标的雷达回波模拟及成像[J].电子学报,1995, 23(9): 28-31.)

[15] Liu C J, Chen W T, Chen Z P. Orbit object ISAR echo signal simulation[J].ComputerSimulation, 2006, 23(10): 296-300. (刘朝军,陈文彤,陈曾平. 轨道目标ISAR中频回波模拟技术研究[J].计算机仿真, 2006, 23(10): 296-300.)

[16] Howard D C.Orbitmechanics[M].trans. Zhou J H, Xu B, Feng Q S.Beijing: Science Press, 2009:25-32,120-203. (Howard D.轨道力学[M].周建华,徐波,冯全胜，译.北京:科学出版社,2009:25-32,120-203.)

[17] Ovliver M, Eberhard G.Satelliteorbits:models,methodsandapplications[M].2nd ed. New York：Springer-Verlag Berlin Heidelberg2001: 157-168.

[18] Dong J, Shang C X, Gao M G, et al. Research on bistatic ISAR speed compensation of space target[J].JournalofCAEIT, 2010, 5(1): 78-85. (董健,尚朝轩,高梅国, 等. 空间目标双基地ISAR成像的速度补偿研究[J].中国电子科学研究院学报,2010, 5(1): 78-85.)

Bistatic ISAR echo simulation of space target based on two-body model

GUO Bao-feng1,2, SHANG Chao-xuan1, WANG Jun-ling2, GAO Mei-guo2

(1. Department of Electronic and Optical Engineering, Ordance Engineering College, Shijiazhuang 050003, China;2. School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)

Aiming at the imaging problem of space target, a bistatic inverse synthetic aperture radar(ISAR) echo simulation method based on a two-body model is proposed. The method simulates the orbital characteristics of space target based on the two-body model. The three-dimensional scatter model is built, the high speed movement and attitude stabilization are under consideration. Then the bistatic ISAR echo data is generated, and the determination method of target visible area relative to bistatic radar is given. Simulation results show that the error between the two-body model and real target orbit is small and the imaging results perfectly reflect the target attitude change. The echo simulation method based on the two-body model helps the accurate imaging of the space target and has an important guiding influence on imaging experiments.

bistatic inverse synthetic aperture radar(ISAR); two-body model; space target; echo simulation

2015-10-19；

2016-02-18；网络优先出版日期：2016-06-08。

国家自然科学基金(61401024)；北京理工大学基础研究基金(20140542001)资助课题

TN 957

A

10.3969/j.issn.1001-506X.2016.08.10

郭宝锋(1987-),男,博士研究生,主要研究方向为雷达信号处理、雷达成像技术。

E-mail: guobao_feng870714@126.com

尚朝轩(1964-),男,教授,博士研究生导师,主要研究方向为电子装备性能检测与故障诊断、雷达信号处理。

E-mail: scx1207@sina.com

王俊岭(1982-),男,博士,讲师,研究方向为空间目标探测、实时信号处理、雷达成像技术。

E-mail: emailwjl@gmail.com

高梅国(1965-),男,教授,博士研究生导师,主要研究方向为信号与图像处理、信息安全与对抗理论与技术、目标探测与识别理论与技术。

E-mail: meiguo_g@bit.edu.cn

网络优先出版地址：http:∥www.cnki.net/kcms/detail/11.2422.TN.20160608.0852.004.html