基于降维稀疏重构的相干信源二维DOA估计方法

王秀红, 毛兴鹏, 张乃通

(1. 哈尔滨工业大学电子与信息工程学院, 黑龙江 哈尔滨 150001;2. 哈尔滨工业大学(威海)信息与电气工程学院, 山东 威海 264209;3. 哈尔滨工业大学信息感知技术协同创新中心, 黑龙江 哈尔滨 150001)



基于降维稀疏重构的相干信源二维DOA估计方法

王秀红1,2, 毛兴鹏1,3, 张乃通1

(1. 哈尔滨工业大学电子与信息工程学院, 黑龙江 哈尔滨 150001;2. 哈尔滨工业大学(威海)信息与电气工程学院, 山东 威海 264209;3. 哈尔滨工业大学信息感知技术协同创新中心, 黑龙江 哈尔滨 150001)

直接将压缩感知(compressed sensing,CS)思想应用到相干信源二维波达方向(direction of arrival,DOA)估计中会带来高计算复杂度的问题。为了解决这一问题,提出了一种基于降维稀疏重构的二维DOA估计方法,该方法利用特殊阵列结构将二维冗余字典构建问题转化为一维冗余字典的构建,同时提出了一种基于子字典空间谱重构的配对算法,从而在极大降低算法计算复杂度的同时,提高了配对成功概率。仿真结果表明,该方法对相干信源具有接近于克拉美罗下界(Cramér-Rao lower bound, CRLB)的估计性能,即使是在低信噪比、少快拍数和小角度间隔的情况下,仍有良好的估计性能。

波达方向; 二维波达方向估计; 相干信源; 降维稀疏重构; 冗余子字典

0　引　言

近年来高精度、高分辨率的波达方向(direction of arrival,DOA)估计方法得到了快速的发展并且成功应用于雷达、声纳和无线通信等领域[1]。这些方法绝大多数都是针对多信源的一维方向(比如方位角)估计。但是在很多应用中目标到达角却具有二维特性(比如方位角和俯仰角),因此二维DOA估计方法得到了广泛的关注和深入的研究[2-13]。

经典的子空间类方法已经成功地应用到了二维DOA估计中[4-5],比如二维多重信号分类(multiple signal classification,MUSIC)算法[4]和二维旋转不变技术估计信号参数(estimate signal parameter via rotational invariance technique,ESPRIT)算法[5]等,虽然该类方法具有高分辨率、高估计精度等优点,但它们的应用前提也较为苛刻,比如要求大量的快拍数、信源之间的独立性、噪声为不相关的白噪声等。很多实际应用环境都无法满足上述条件,这使得很多基于子空间类的估计方法因性能严重下降而失效。因此,在各种复杂的环境和复杂电磁干扰的背景下,如何抑制强相关甚至相干信源的影响并且快速估计出目标信源的二维DOA角度,是一个具有重要的实际应用价值的课题方向。在这方面国内外的学者已经取得了一定的研究进展[6-21]。文献[7]采用了前后向空间平滑(forward backward spatial smoothing, FBSS)[6]技术对信号去相干,而后利用二维ESPRIT 算法进行角度估计;文献[8-9]通过对接收数据的互协方差矩阵重构实现解相干,重建信号子空间后采用ESPRIT等算法估计目标DOA;文献[10]在三维垂直阵列上利用波达方向矩阵法实现解相干,并将二维DOA估计问题转化为3个一维DOA估计问题进行处理;文献[11]通过对接收数据构建成Toeplitz结构的矩阵实现了信源的解相干;文献[12]通过将接收数据的四阶累积量构建成Toeplitz矩阵结构实现信源的解相干;文献[13]提出利用斜投影的方法将相干信源和非相干信源分离,从而实现所有信源的二维角度估计。

近年来发展起来的压缩感知(compressed sensing,CS)技术也已经成功应用到了DOA估计中[14-19]。该类方法由于不需要利用接收数据的统计特性,因而无需任何预处理即可对相干信源实现DOA估计;同时由于不需要进行特征分解和空间平滑技术,并且可单快拍处理,所以具有低计算复杂度的优点;因此,该类方法具有重要的实用价值和广泛的应用前景。目前基于CS的DOA估计方法主要应用于均匀线阵[14-15],也即一维DOA估计中。而针对面阵的二维CS DOA估计目前文献较少,其主要原因之一就是CS方法中需要构建的二维角度冗余字典长度过长,使得算法的复杂度太高,难以实现,从而无法直接将其应用于二维DOA估计中。为了解决这个问题,文献[16]利用L型阵列的特殊结构,提出了一种空间角度稀疏表示的方法,将二维DOA角度解耦并转变为两个一维DOA估计的问题,但是该方法的配对算法在信源功率相近甚至相等时将会失效。文献[17]对接收数据的互相关矩阵进行稀疏表示来实现二维角度估计,但是无法实现对相干信源的估计。

为了解决相干信源二维CS DOA估计的低复杂度问题,本文提出了一种基于降维稀疏重构(reduction dimension sparse reconstruction,RDSR)的DOA估计方法。该方法利用十字型阵列结构特点,将二维DOA角度冗余字典的构建转化为两个一维的角度冗余字典的构建,从而大大降低算法的计算复杂度,并且提出了基于冗余子字典的二维空间谱重构的配对方案,从而克服了文献[16]配对算法的缺陷。

因此,本文方法的优势主要体现在以下几个方面:①无需空间平滑等预处理即可实现相干信源的估计;②通过降维处理将二维问题转化为两个一维问题并行处理,大大降低算法复杂度和运行时间;③该方法对快拍数目要求不高,即使单快拍数据也可以完成二维DOA估计。

1　数学模型

1.1系统模型

考虑有K个远场信源入射到一个十字型阵列,如图1所示,该阵列位于x-z平面,由两个分别位于x轴和z轴上的均匀线阵垂直交叉构成,其中位于x轴和z轴子阵列的阵元数分别为M和N,阵元间距均匀且分别为dx和dz。假设第k个信源入射到天线阵列的方位角为θk,俯仰角为φk,其中方位角定义为入射信号在xoy平面上的投影与x轴的夹角,俯仰角定义为入射信号与其在xoy平面投影之间的夹角。

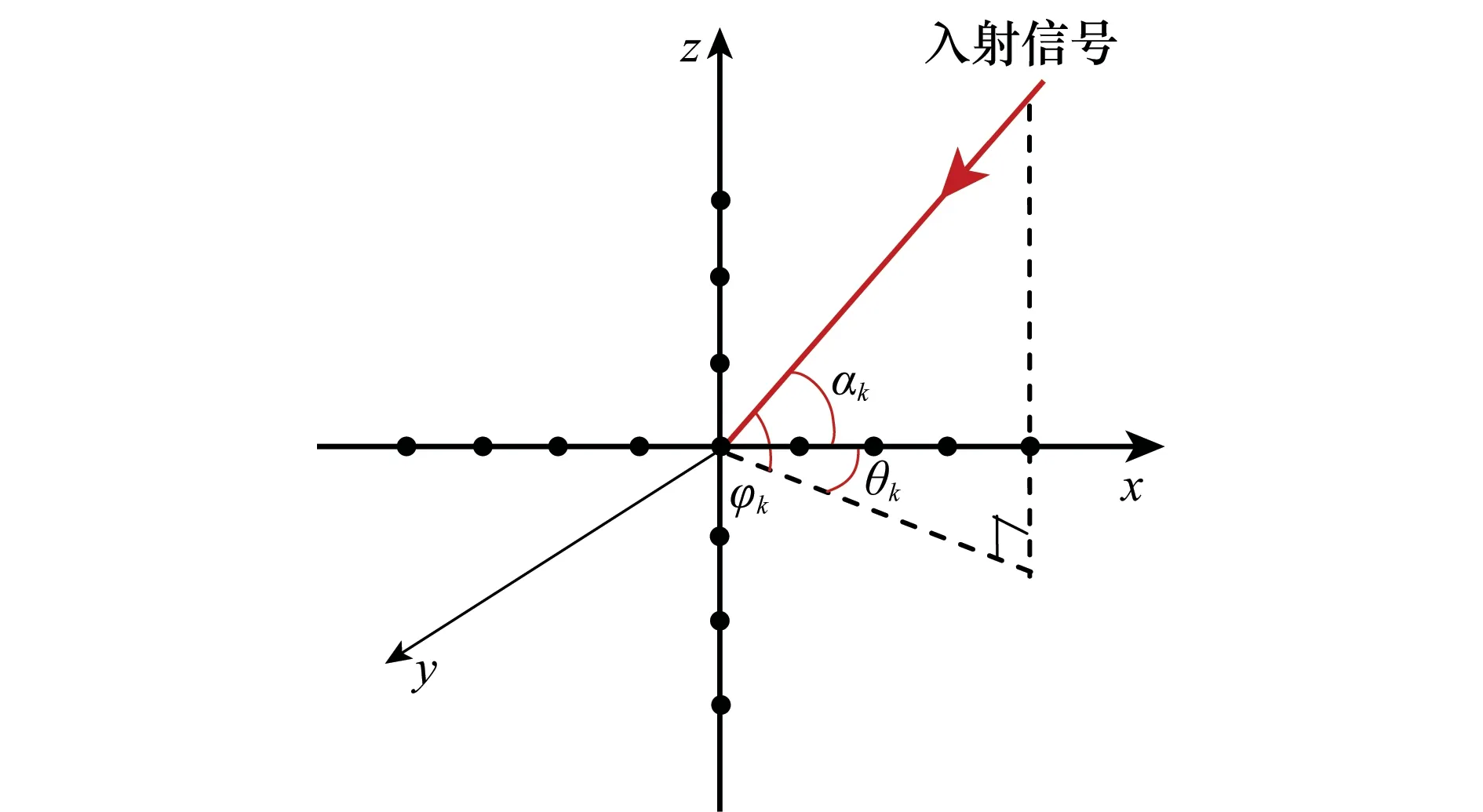
图1　阵列系统模型

该十字阵列(共M+N-1个阵元)的接收信号可以表示为

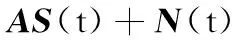
(1)

式中,S(t)=[s1(t),s2(t),…,sK(t)]T为K个入射信号的矢量;N(t)=[n1(t),n2(t),…,n(M+N-1)(t)]T为阵列接收噪声矢量;A为(M+N-1)×K维阵列流形矩阵,可表示为

(2)

式中,a(θk,φk)为导向矢量,其各元素表示为

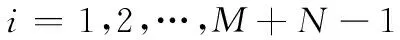
(3)

式中,xi和zi为第i个阵元在xoz平面的坐标位置。

1.2基于CS的二维DOA估计

首先将式(1)的接收信号模型转化为稀疏化模型。利用信源在空域上具有稀疏性的特点,信源矢量S(t)可按照空域角度进行稀疏化表示为稀疏的(Lθ×Lφ)×1维矢量P(t),其中Lθ为待搜索的方位角数目,Lφ为待搜索的俯仰角数目。S(t)稀疏化表示后则需要将阵列流形矩阵A进行列扩展,生成角度冗余字典Ψ,其由所有可能的Lθ×Lφ个二维DOA角度的导向矢量组成。

(4)

因此,二维DOA估计中接收信号的稀疏化模型可表示为

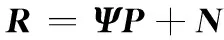
(5)

式中,R=[R(t1),R(t2),…,R(tT)]∈C(M+N-1)×T和P=[P(t1),P(t2),…,P(tT)]∈CL×T分别为阵列接收信号与入射信号的多快拍数据矩阵(其中LLθ×Lφ,T为快拍数)。这样,式(1)的DOA估计问题则转化为对式(5)的稀疏解求解问题,可以通过无约束最小化问题来求解。

(6)

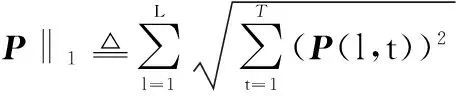
为了描述方便,定义CS框架下的空间谱为

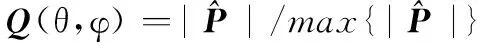
(7)

这样,估计出的二维DOA角度可表示为

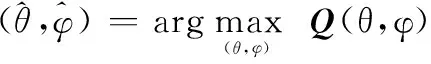
(8)

综上可以发现,二维CSDOA估计的关键和主要的计算量都在于式(6)的求解,而该式求解的复杂度与冗余字典Ψ的维数Lθ×Lφ密切相关,如采用内点法求解,式(6)的求解复杂度约与O(Lθ×Lφ)3[15]成正比。当需要搜索的方位角和俯仰角的数目较多时,冗余字典Ψ的维数Lθ×Lφ很大,此时式(6)的求解复杂度将会是巨大的,并且在实际系统中难以实现,因此限制了该类方法的应用。

2　基于降维稀疏重构二维DOA估计

为了降低上述二维DOA估计算法的复杂度,可以考虑缩减冗余字典Ψ的维数。为此,本文通过将二维DOA角度解耦,把二维DOA估计问题转化为两个一维DOA估计问题,从而大大减小冗余字典Ψ的维数。

2.1降维处理

考虑将图1所示的十字阵看做是两个独立的均匀线阵,即将z轴的子阵列视为一个独立的均匀线阵,可以使用该子阵列估计出入射信号与该子阵列之间的夹角,该夹角为π/2-φ,因此可以利用z轴子阵列估计出俯仰角φ∈[-π/2,π/2];同理,可以使用x轴的子阵列估计出入射信号与该子阵列之间的夹角,即入射信号与x轴的夹角α(为了表述方便,将夹角α称为合成角),其与方位角θ和俯仰角φ之间有如下关系

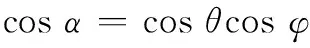
(9)

因此,只要能够利用子阵列求出俯仰角φ和合成角α,就可根据式(9)求出方位角θ∈[0,π]。

将z轴和x轴子阵列接收的信号分别表示为

(10)

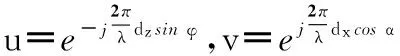
类似于第1.2节中的稀疏化过程,由式(10)得到其稀疏表示模型

(11)

式中,ΦZ和ΦX分别为z轴和x轴子阵列的冗余字典,由AZ和AX扩展而成,即

(12)

(13)

可将式(11)的单快拍模型推广到多快拍模型

(14)

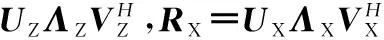
(15)

式(15)的稀疏解可表示为

(16)

需要注意的是,式中F范数部分代表重构误差, l1范数部分代表稀疏性,即DOA估计误差,而参数μ1和μ2则的选择方法同式(6),它们用来控制重构误差与稀疏性之间的折中关系,即调节两者在整体误差中所占的比重。

利用求解出的稀疏解分别生成一维空间谱

(17)

找出K个最大的谱峰对应的角度,即为各信源的俯仰角和合成角

(18)

2.2角度配对存在的问题

(19)

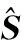
同时,我们还发现在求解式(16)的问题中,参数μ1和μ2的选择对估计误差和配对成功概率影响较大。对于文献[16]中基于幅度排序的配对方案,为了保证尽可能大的配对概率,因此在选择参数μ时要求幅度估计误差项所占比重较大(即要使幅度估计误差最小),这样位置估计误差项比重就会较小,从而导致DOA估计误差较大。所以这种配对算法会出现在信噪比较高的情况下DOA估计误差较大的问题。

2.3基于子字典的角度配对方案

为进一步提高角度配对的成功概率和DOA估计性能,提出一种基于冗余子字典空间谱重构的角度配对方案。

首先需要构建冗余子字典(为了方便区分,将上节提到的冗余字典称为完全冗余字典,简称全字典,而此处构建的冗余子字典简称为子字典),其具体构建方法如下。

假设系统中有K个入射信源,从第2.1节的方法中估计出它们的俯仰角为{φ1,…,φK}和合成角为{α1,…,αK},那么按照排列组合方案将形成I=K2个组合方案,将其表示为

(20)

(21)

(22)

由集合Ω内所有角度生成的导向矢量构成矩阵

(23)

(24)

由于子字典是全字典的一部分,仍然满足式(5)的DOA稀疏模型,故有

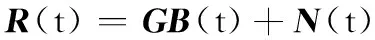
(25)

因此,可重构出压缩感知框架下的二维空间谱为

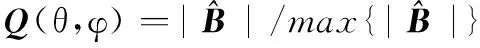
(26)

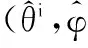
(27)

需要注意的是,由于在每个子字典下至多只有一个信源存在,因此对于子字典半径Dθ,Dφ和间隔Δθ,Δφ的选取只需保证空间谱的稀疏性即可;同时,由于至多只有一个信源存在,所以对式(25)求解稀疏解算法的精度和分辨率要求也不高,因此除了式(6)的方法之外,还可以采用低复杂度的贪婪算法,比如正交匹配追踪(orthogonalmatchingpursuit,OMP)[14]算法等。

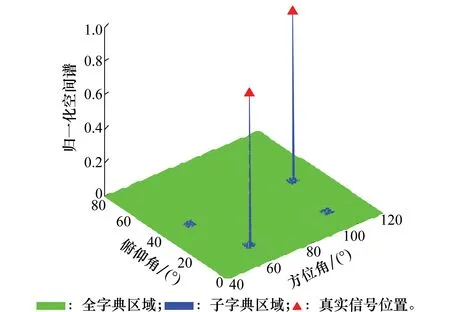
图2　基于子字典的配对方案举例(两个相干信源)

以上所述的基于子字典的配对方案,基本不受2.1节重构算法误差的影响,并且对信噪比要求不高,对于信源功率相等或相近的情况仍适用,从而可以大大提高角度配对成功概率。

综上,本文提出的RDSR算法的流程归纳如下:

步骤 1根据式(12)和式(13)构建子阵列的一维冗余字典ΦZ和ΦX;

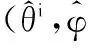
3　数值仿真

为了验证本文方法的有效性,本文将从下面几个方面来仿真分析算法的性能。仿真中采用图1所示的十字型阵列,其中每个子阵列的阵元数M=N=11,阵元间隔为半波长。仿真中对信源的估计精度采用均方根误差(rootmeansquareerror,RMSE)来表征,其具体定义为

3.1信源幅度相同时DOA估计结果

图3为100次独立实验的3个相干信源二维DOA估计结果,其中每个信源的幅度相同,SNR为0dB,快拍数为100。从图3可以看出,当信源的幅度相同时,文献[16]的方法会出现错误配对的情况,而导致算法失效,而本文方法不存在这种情况,可以较准确的估计出信源的二维DOA角度。

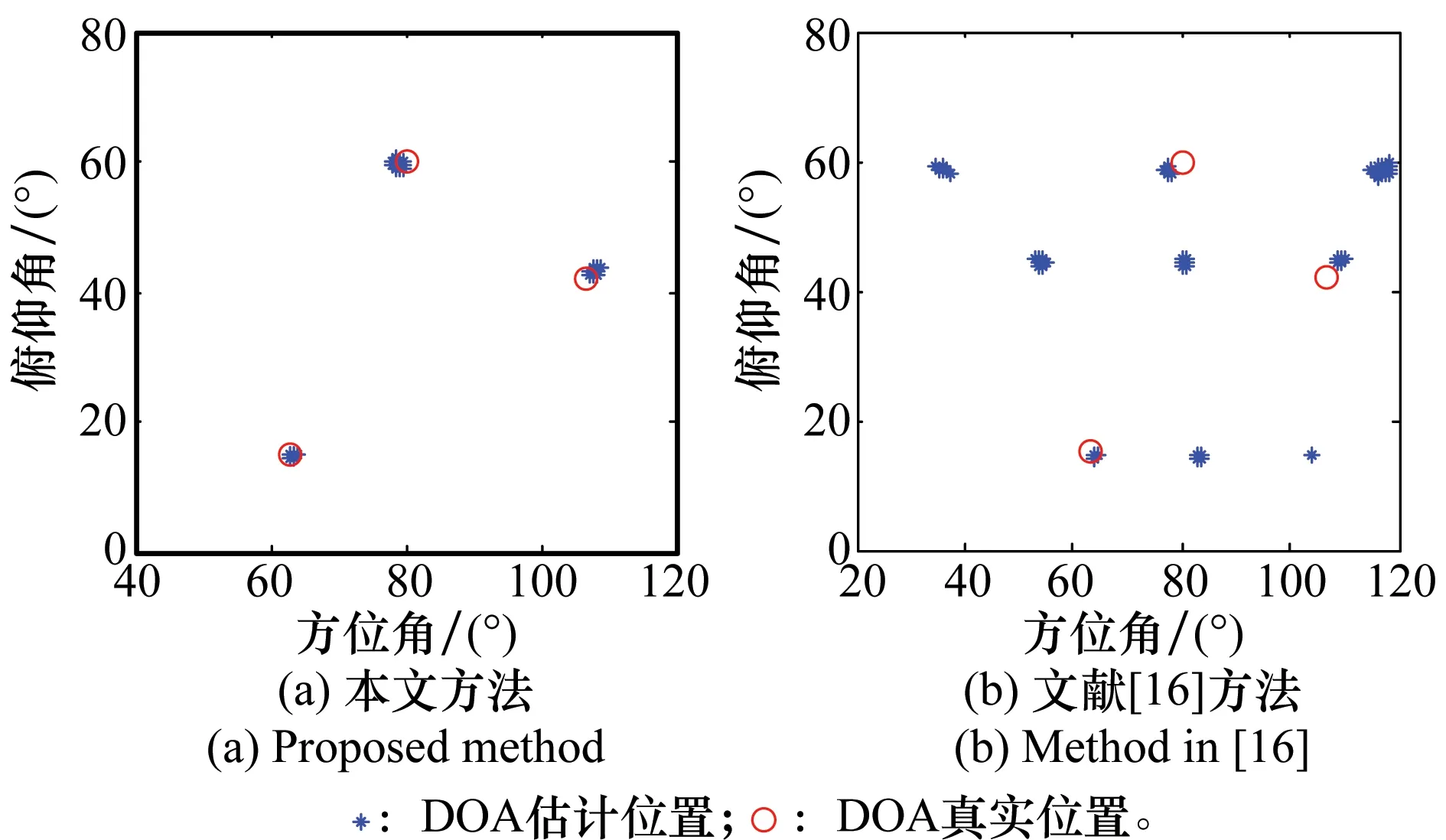
图3　二维DOA估计结果对比

3.2信噪比对算法性能影响

图4给出了2个相干信源在幅度比为1∶1情况下各种算法的估计误差和配对成功概率比较。仿真中两个信源角度分别为[θ1,φ1]=[63°,15°],[θ2,φ2]=[107°,42°],快拍数为100。从图4可以看出,当信源幅度相同时,文献[16]的方法由于配对失败而导致估计性能很差,即这种情况下该方法已失效,而文献[7]中基于FBSS的方法和本文方法都能较准确地估计出信源角度,但在低信噪比下,本文方法的估计性能则优于FBSS方法,且性能更接近CRB。同时,相对于FBSS方法只适用于由均匀线阵构成的阵列这一缺点,本文算法则也可以适用于由非均匀线阵构成的阵列,但由于篇幅有限本文不做深入讨论。

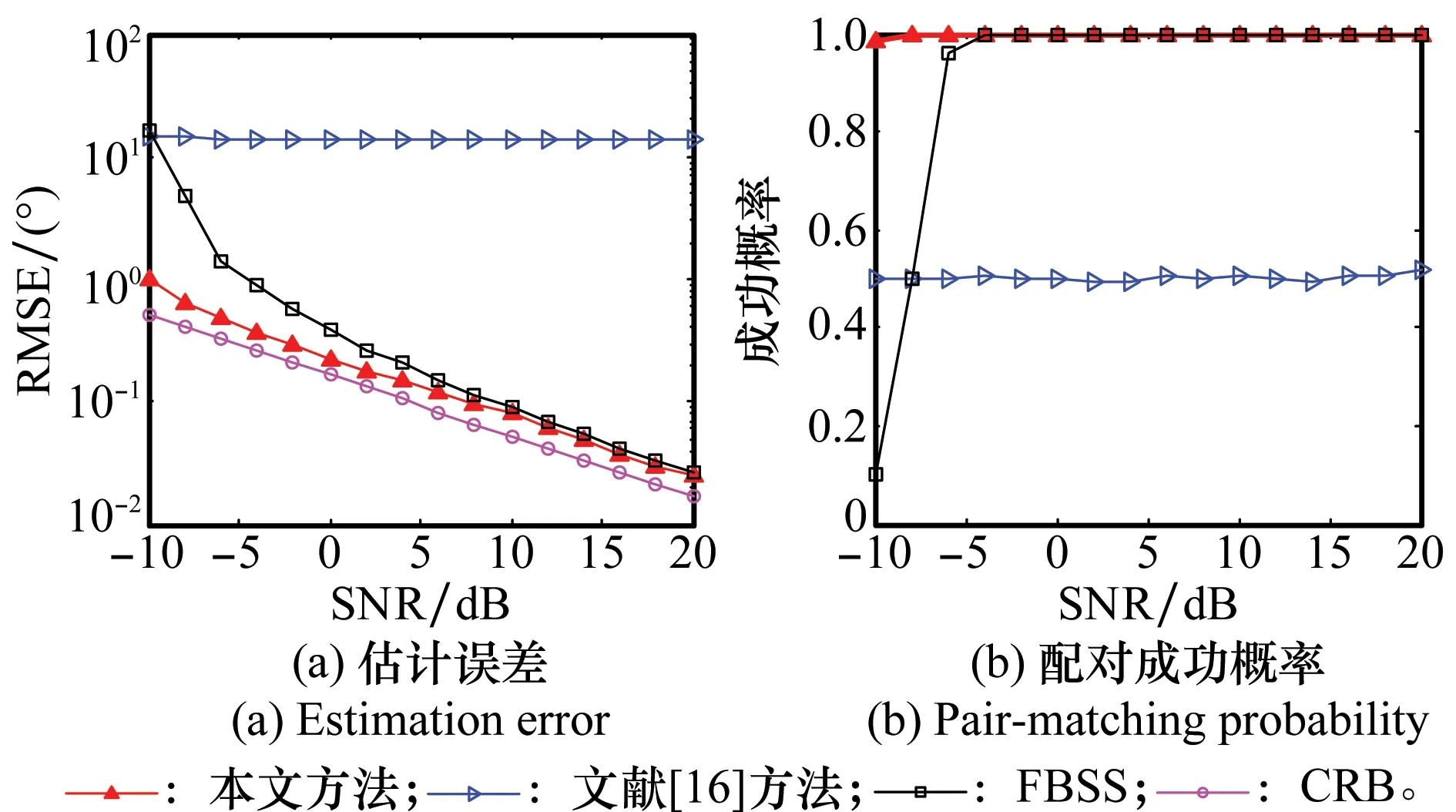
图4　相干信源DOA估计性能随信噪比变化曲线

3.3信源角度间隔对算法性能影响

图5给出了两个相干信源在幅度比为0.8∶1情况下二维DOA估计误差与信源角度间隔的变化关系。仿真中角度间隔Δ定义如下:如果设第一个信源的DOA角度为(θ1,φ1),那么与其角度间隔Δ的第二个信源的DOA角度(θ1+Δ,φ1+Δ)。仿真中SNR为10 dB,快拍数为100。从仿真结果来看,在3种不同方法中,本文方法的估计性能最好,且接近于CRB界;文献[16]方法在角度间隔小于10°以内时估计性能优于FBSS方法,而在角度间隔大于10°以上时不如FBSS。

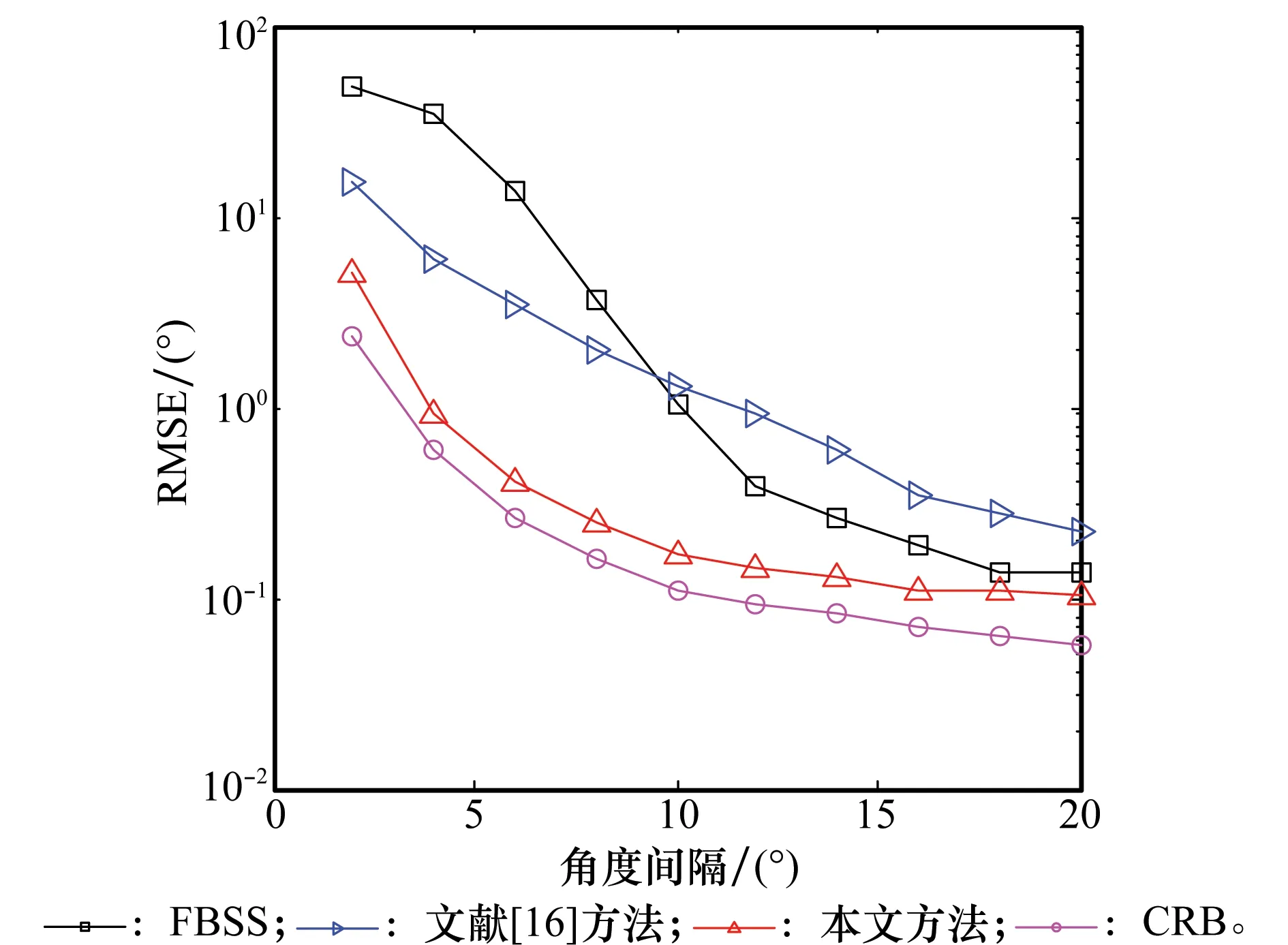
图5　相干信源DOA估计误差随信源角度间隔变化曲线

3.4快拍数对算法性能影响

图6给出了SNR分别为-10 dB、0 dB和10 dB情况下二维DOA估计误差与快拍数的变化关系曲线。仿真中两个相干信源的幅度比为1∶1,信源角度同上。从仿真结果来看,在不同的信噪比下和不同的快拍数目条件下,本文算法都具有接近于CRB的估计性能,而FBSS方法则在低信噪比情况下估计性能很差,即使增加快拍数,性能也得不到明显改善。同时值得注意的是,本文算法在单快拍的情况下也可工作,而FBSS算法不能。

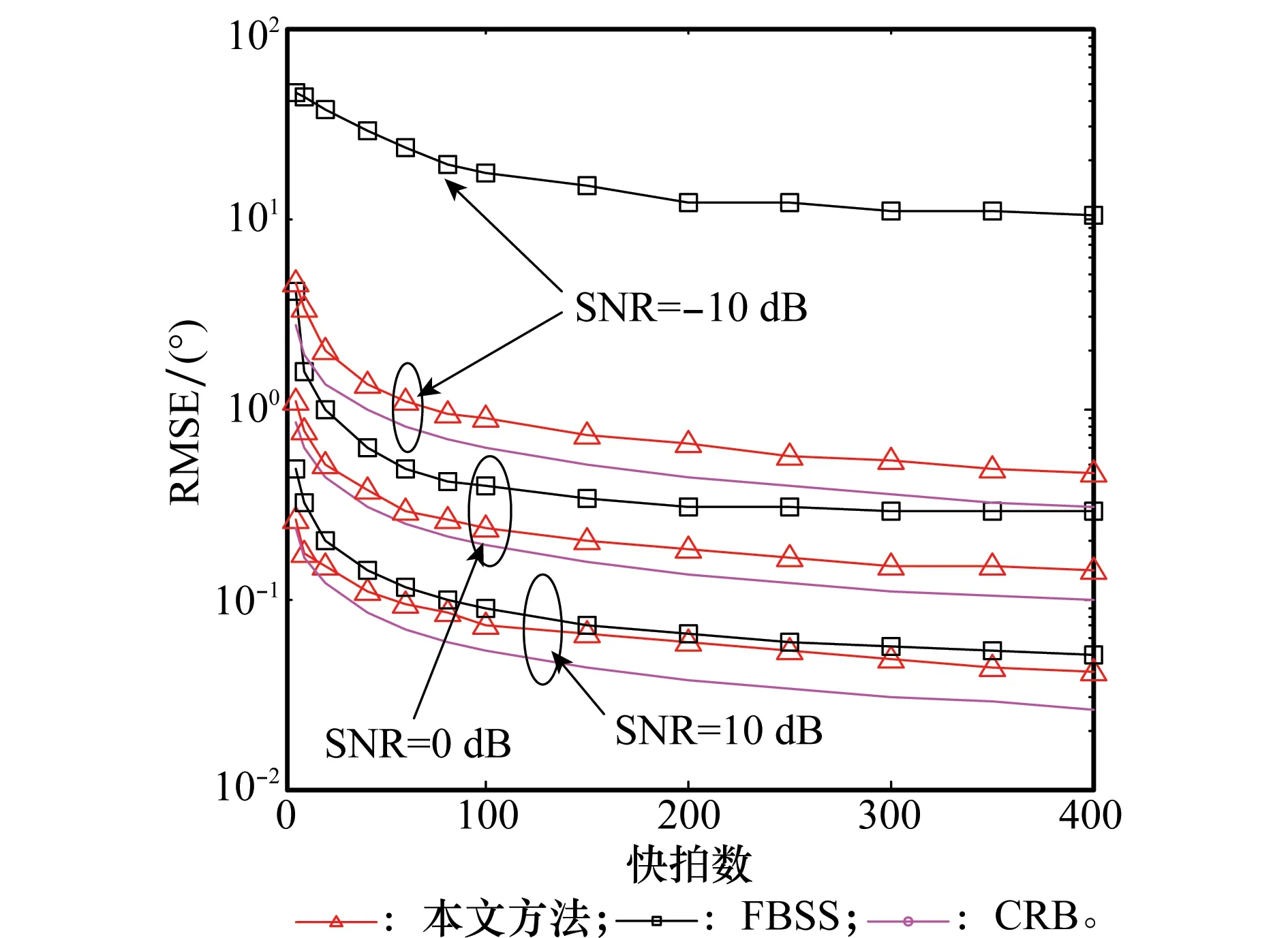
图6　相干信源DOA估计误差随快拍数变化曲线

4　复杂度分析

在采用CS理论进行二维DOA估计时,如果直接进行二维角度搜索,那么DOA估计算法的复杂度将与角度冗余字典的规模大小密切相关。同时,估计中采用不同的稀疏重构算法复杂度也不相同。结合本文二维DOA估计背景,将几种常见的稀疏分解算法(OMP算法[14]和L1-SVD算法[15])的复杂度如表1所示。

表1　几种常用算法与本文算法的复杂度对比

注:K为信源数;M为阵元总数;T为快拍数;Lθ,Lφ和Lsd分别为方位角、俯仰角和子字典的搜索角度数。

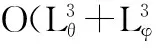
表2给出了不同DOA估计算法的运行时间和估计误差的对比,其中“运行时间”是由计算机通过Matlab软件进行100次统计算法的运行时间并平均后得到的。假设2个相干信源,信源角度同第3.2节,子阵元数为M=N=11,SNR=10dB,快拍数为100,方位角和俯仰角的冗余字典大小都为400,角度间隔均为0.2°。从表2中可以看出,降维处理可以极大地降低算法的复杂度,并且几乎不会带来估计精度的损失,同时,本文方法与文献[16]的方法比较,算法复杂度相差不多,但是本文方法的估计精度更高。

表2　不同DOA估计算法的运行时间和估计误差对比

5　结　论

本文提出了一种RDSR的DOA估计方法,以实现低复杂度的相干信源二维DOA估计问题,同时该方法也成功解决了当信源幅度或功率相同或相近时配对算法失效的问题。仿真结果表明,本文方法在低信噪比、小角度间距以及少快拍数情况下都具有良好的估计性能,并且估计误差可以接近于克拉美罗界。另外,与直接应用CS进行二维DOA搜索的估计方法相比,本文方法具有更低的计算复杂度。

[1] Krim H, Viberg M. Two decades of array signal processing research: The parametric approach[J].IEEESignalProcessingMagazine, 1996, 13(4): 67-94.

[2] Nie X, Li L P. A computationally efficient subspace algorithm for 2-D DOA estimation with L-Shaped array[J].IEEESignalProcessingLetters, 2014, 21(8): 971-974.

[3] Gu J F, Zhu W P, Swamy M N S. Joint 2-D DOA estimation via sparse L-shaped array[J].IEEETrans.onSignalProcessing, 2015, 63(5): 1171-1182.

[4] Chan A Y J, Litva J. MUSIC and maximum techniques on two-dimensional DOA estimation with uniform circular array[J].IEEProceedings-Radar,SonarandNavigation, 1995, 142(3): 105-114.

[5] Kedia V S, Chandna B. A new algorithm for 2-D DOA estimation[J].SignalProcessing, 1997, 60(3): 325-332.

[6] Pillai S U, Won B H K. Forward/backward spatial smoothing techniques for coherent signals identification[J].IEEETrans.onAcousticsSpeechandSignalProcessing, 1989, 37(1): 8-15.

[7] Cheng Q, Zhao Y, Yang J. A Novel 2-D DOA estimation for coherent signals based on L-shaped array[C]∥Proc.oftheInternationalConferenceonWirelessCommunicationandSignalProcessing, 2012, 7363(1): 1-5.

[8] Palanisamy P, Kalyanasundaram N, Swetha P M. Two-dimensional DOA estimation of coherent signals using acoustic vector sensor array[J].SignalProcessing, 2012, 92(7): 19-28.

[9] Liu Z T, Ruan X Y, He J. Efficient 2-D DOA estimation for coherent sources with a sparse acoustic vector-sensor array[J].MultidimensionalSystemsandSignalProcessing, 2013, 24(1): 105-120.

[10] Wang L, Li G L. A new method for estimating 2-D DOA in coherent sources environment using single snapshot[J].TransactionsofBeijingInstituteofTechnology, 2015, 35(5): 512-518. (王凌, 李国林. 利用单次快拍实现相干信源二维测向的新算法[J].北京理工大学学报, 2015, 35(5): 512-518.)

[11] Chen H, Zhang X. Two-dimensional DOA estimation of coherent sources for acoustic vector-sensor array using a single snapshot[J].WirelessPersonalCommunications, 2013, 72(1): 1-13.

[12] Chen H, Hou C P, Wang Q, et al. Cumulants-based toeplitz matrices reconstruction method for 2-D coherent DOA estimation[J].IEEESensorsJournal, 2014, 14(8): 2824-2832.

[13] Tao H, Xin J M, Wang J S, et al. Two-dimensional direction estimation for a mixture of no coherent and coherent signals[J].IEEETrans.onSignalProcessing, 2015, 63(2): 318-333.

[14] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J].IEEETrans.onInformationTheory, 2007, 53(12): 4655-4666

[15] Malioutov D, Cetin M, Willsky A. S. A sparse signal reconstruction perspective for source location with sensor arrays[J].IEEETrans.onSignalProcessing, 2005, 53(8): 3010-3022.

[16] Li P F, Zhang M, Zhong Z F. Two dimensional DOA estimation based on sparse representation of space angle[J].JournalofElectronics&InformationTechnology, 2011, 33(10): 2402-2406. (李鹏飞,张旻, 钟子发. 基于空间角稀疏表示的二维DOA估计[J].电子与信息学报,2011,33(10):2402-2406.)

[17] Luo X Y, Fei X C, Wei P, et al. Sparse representation-based method for two-dimensional direction-of-arrival estimation with L-shaped array[C]∥Proc.oftheIEEEInternationalConfe-renceonCommunicationProblem-solving, 2014: 277-280.

[18] Northardt E T, Bilik I, Abramovich Y I. Spatial compressive sensing for direction-of-arrival estimation with bias mitigation via expected likelihood[J].IEEETrans.onSignalProcessing, 2013, 61(5): 1183-106.

[19] Massa A, Rocca P, Oliveri G. Compressive sensing in electromagnetics-a review[J].IEEEAntennasandPropagationMagazine, 2015, 57(1): 224-238.

[20] Hansen P C, O’ Leary D P. The use of the L-curve in the regularization of discrete ill-posed problems[J].SiamJournalonScientificComputing, 1993, 14(6): 1487-1503.

[21] Heng Y, Lu S, Mhamdi A, Pereverzev S V. Model functions in the modified L-curve method case study: the heat flux reconstruction in pool boiling[J].InverseProblems, 2010, 26(5): 55006-55018.

Two-dimensional DOA estimation for coherent sources based on reduction dimension sparse reconstruction

WANG Xiu-hong1,2, MAO Xing-peng1,3, ZHANG Nai-tong1

(1. School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001, China; 2. School of Information and Electrical Engineering, Harbin Institute of Technology(Weihai), Weihai 264209, China; 3. Collaborative Innovation Center of Information Sensing and Understanding at Harbin Institute of Technology, Harbin 150001, China)

The problem of high computational complexity will be caused if compressed sensing (CS) is directly applied to two-dimensional (2-D) direction of arrival (DOA) Estimation of coherent sources. To solve this problem, a 2-D DOA estimation method based on reduction dimension sparse reconstruction (RDSR) is proposed. The proposed method converts the construction of a 2-D redundancy dictionary into that of a 1-D dictionary by using the special array structure. In addition, a pair-matching scheme is proposed based on spatial spectrum reconstruction of the sub-dictionary. Therefore, the proposed method not only reduces the computational complexity but also improves the pairing probability of success. Simulation results show that the estimated performance of the method is close to the Cramér-Rao lower bound (CRLB), even in the case of low signal-to-noise ratio (SNR), small number of snapshots and small angle interval, the estimation performance is still good.

direction of arrival (DOA); two-dimensional (2-D) DOA estimation; coherent sources; reduction dimension sparse reconstruction (RDSR); redundant sub-dictionary

2015-11-15；

2016-02-28；网络优先出版日期：2016-06-07。

国家自然科学基金(61171180, 61371100)资助课题

TN 953.3

A

10.3969/j.issn.1001-506X.2016.08.01

王秀红(1978-),女,讲师,博士研究生,主要研究方向为阵列信号处理、波达角度估计。

E-mail:xiuhongwang@hit.edu.cn

毛兴鹏(1972-),男,教授,博士研究生导师,主要研究方向为电子侦察与电子对抗、弱信号检测、雷达信号处理。

E-mail:mxp@hit.edu.cn

张乃通(1934-),男,中国工程院院士,教授,主要研究方向为信号处理、专用移动通信系统、卫星通信、深空通信。

E-mail:ntzhang@hit.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160607.1605.020.html