基于全局最小熵的随机稀疏调频步进信号运动补偿方法

吕明久, 李少东, 杨　军, 马晓岩

(1.空军预警学院研究生队, 湖北 武汉 430019; 2. 空军预警学院, 湖北 武汉 430019)



基于全局最小熵的随机稀疏调频步进信号运动补偿方法

吕明久1, 李少东1, 杨军2, 马晓岩2

(1.空军预警学院研究生队, 湖北 武汉 430019; 2. 空军预警学院, 湖北 武汉 430019)

发射频率和孔径二维随机稀疏的调频步进信号,可降低雷达系统对采样率的要求,同时可提高抗干扰能力。但是调频步进信号随机稀疏时会带来运动补偿困难的问题。针对此问题,提出一种基于全局最小熵的运动补偿方法。首先,利用全局最小熵方法完成包络对齐;其次将初相校正问题转换为径向速度与加速度的参数估计问题。为实现速度的高精度估计,采取粗搜索与精估计相结合,以全局最小熵作为代价函数,基于黄金分割法进行变步长搜索实现参数的快速高精度估计,最终完成初相校正。理论分析和仿真结果表明该算法具有参数估计速度快、估计精度高且在较低的信噪比条件下具有较高稳健性的优势。

随机稀疏调频步进信号; 运动补偿; 黄金分割法; 全局最小熵; 一维距离像

0　引　言

调频步进信号通过连续发射载频跳变的调频步进子脉冲实现大的合成带宽,以获得高的距离分辨率,具有硬件要求低、合成带宽大、成本低等特点[1]。而随机稀疏调频步进信号在距离向稀疏可提高雷达系统的抗干扰能力,方位向(孔径)稀疏符合相控阵雷达的多工作模式。当发射的调频步进信号频率和孔径二维随机稀疏时,由目标运动带来的运动补偿将变得困难。

目前，调频步进信号运动补偿方法研究主要包括3方面。一是利用辅助信息进行补偿,最常用的是通过窄带测速得到目标的运动信息[2]。这类方法主要问题是参数估计误差大、补偿精度较低。二是运动参数估计法。主要是利用脉冲间的相关性通过时域法、频域法、最小熵(最大对比度)法等估计目标运动参数[3-8]。三是基于特定波形的参数估计方法,如针对最常用正负步进频率波形[9-14],相应的速度估计算法主要有相位差分法[11]、脉组误差法[12]、脉组求和法[13-14]等。上述方法大多是基于完整数据条件下的运动参数估计,研究随机稀疏步进信号主要还是基于运动补偿已经完成或者是基于转台模型[15-19],忽略了回波信号稀疏对运动补偿算法带来的不利影响。

本文针对随机稀疏调频步进信号进行运动补偿使用现有算法效果较差的问题,利用全局类算法对信号稀疏不敏感的特点,提出了一种基于全局最小熵的随机稀疏调频步进信号运动补偿算法。该算法分为包络对齐与初相校正两步。首先通过全局最小熵方法得到包络对齐后的脉冲一维距离像,再以全局最小熵作为代价函数,通过黄金分割法对速度、加速度进行估计。其中,为提高速度估计精度,对速度进行二次估计,第一次为粗速度估计,第二次为精速度估计,进而完成初相校正。理论分析和仿真结果表明该算法具有以下特点:估计精度高、复杂度低、运算量小,且在低信噪比条件下依然稳健。

1　随机稀疏调频步进回波模型

这里的随机稀疏调频步进信号每组脉冲串中频率随机稀疏,同时方位向也存在孔径稀疏。随机稀疏调频步进信号的示意图如图1所示。图中虚线部分代表的是缺失子脉冲,且每组脉冲缺失的子脉冲互不相同。每组脉冲代表一个子孔径,其中无色部分代表缺失的子孔径。下面对回波进行建模。

图1　稀疏调频步进信号波形示意

传统调频步进信号基带回波[20]可表示为

(1)

(2)

式中,tl,m为第m组脉冲的慢时间序列;Φa为孔径稀疏随机置零矩阵,可以从M×M维单位矩阵随机置零M-M′行得到;Φm为频率随机置零矩阵,可以通过N×N维单位矩阵随机置零N-N′行得到。因此,对于频率、孔径随机稀疏的调频步进信号,其回波表达式为

(3)

式中,Γm表示第m个脉组中N′个子脉冲的频率步进规律,具体可以表示为

(4)

假设目标沿雷达径向的速度为ν,径向加速度为a,此时目标离雷达的距离可以表示为

(5)

式中,R0为参考距离。回波信号经子脉冲压缩的结果[20]为

(6)

当脉间发生走动时,首先需进行包络对齐。稀疏孔径条件下的包络对齐方法将在后文给出,为便于分析,假设包络对齐已完成,在tn=tl,m+ta+2R0/c时刻对子脉冲信号进行采样,最终得到M′组回波采样矩阵Su(v,a)为

(7)

式中

式中,⊗表示Hadarmard积;s(m,n)为距离成像所需的相位信息;um,n(v,a)为目标运动引入的相位项,具体可以表示为

(8)

对于传统调频步进信号脉压主要包括子脉冲压缩以及子脉冲间脉冲压缩两个步骤:首先对接收的子脉冲进行匹配滤波处理,得到目标的“一维粗距离像”,然后对各组子脉冲进行快速逆傅里叶变换(inversefastFouriertransform,IFFT),最终得到目标的高分辨率一维距离像[20]。当目标运动时,必须进行运动补偿后才能进行第二次脉压处理[2],否则将会导致走动、散焦等问题,这不仅影响距离向成像,还会使得后续方位向散焦,因此必须对相位时移项加以补偿。从式(7)和式(8)可看出,回波信号Su(v,a)同样包含目标运动带来的相位项[u1,n(v,a),…,um,n(v,a),…,uM′,n(v,a)],需要在二次脉压前补偿掉。下面详细研究随机稀疏调频步进信号运动补偿方法。

2　随机稀疏调频步进信号运动补偿

2.1信号稀疏的影响

传统的调频步进信号在进行运动参数估计补偿时大多利用的是相邻脉组中对应载频的子脉冲进行相关处理[4,12]或者对一维距离像进行参数搜索补偿,并利用评价指标(最小熵、对比度等)进行精度判别的方式[3,5,7]。在信号不稀疏的情况下,这些方法具有较好的估计精度且处理简单。但是由于上述方法利用回波信号部分信息进行处理,因此当信号频率、孔径二维稀疏时,受到信号稀疏的影响较大。当信号频率稀疏时,传统利用一个脉组的距离像进行运动参数估计的方法由于子脉冲的部分缺失而导致距离像的旁瓣较高,这无疑增大了参数估计的难度,使得估计精度降低。另外,当信号孔径稀疏时,传统利用相邻脉组子脉冲进行相关处理的方法将会由于子脉冲的空缺而误差增大甚至失效。此外,这类方法对于具有加速运动的目标估计效果较差。总结上述分析,对于频率、孔径二维随机稀疏的调频步进信号,传统运动补偿算法存在的主要问题有以下几点:

(1) 由于只利用了信号的部分信息进行参数估计,受到信号稀疏的影响将会增大;

(2) 当信号稀疏时,估计精度将会大大降低,甚至失效;

(3) 传统利用子脉冲相关性的算法对具有加速度的运动目标参数估计性能较差。

传统的这类方法由于只利用了部分回波信息进行运动参数估计,因此“抵抗”稀疏的性能较差。因此本文利用全局类方法对信号稀疏不敏感的思想对随机稀疏调频步进信号进行运动补偿,下面具体进行分析。

2.2基于全局最小熵的运动补偿方法

针对频率、孔径随机稀疏的调频步进信号,类似常规处理思想,本文将其运动补偿分为包络对齐、初相校正两步处理,下面分别进行分析。

2.2.1包络对齐处理

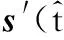
(9)

(10)

由于全局最小熵包络对齐算法在计算全局熵值时运用了全部的包络信息,弥补了脉冲间的不连贯,因此能够完成随机稀疏调频步进频信号回波的包络对齐。

2.2.2初相校正

在完成随机稀疏调频步进信号包络对齐以后,便可得到M′组回波采样矩阵Su(v,a)=[s1,n(v,a),…,sm,n(v,a),…,sM′,n(v,a)]。其中包含由于目标运动带来的相位项[u1,n(v,a),…,um,n(v,a),…,uM′,n(v,a)],必须进行初相校正。由于步进信号子脉冲载频步进变化,因此无法运用传统的PGA法、多普勒中心法等进行初相校正。本文通过估计目标的速度与加速度,构建补偿函数来完成,即

(11)

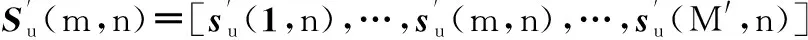
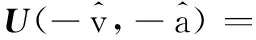
(12)

为运动补偿矩阵。

对于速度、加速度分别进行估计,本文主要从两个方面进行考虑:一是为了避免对速度、加速度熵值二维曲面进行搜索带来的运算量大的问题。二是为进一步提高速度估计精度,将速度估计分成两步进行,即首先对速度进行粗估计,然后进行加速度估计;最后再对速度进行一次精估计,最终得到精确的速度、加速度估计值。

经过式(11)的相位补偿,通过对缺失频点补零后进行IFFT处理便可得到M′组近似的目标一维距离像。

(13)

式中,k=0,1,…,N-1;ξ(N,m)可视为因频点缺失而引入的起伏噪声[22]。需要指出的是,此处利用的IFFT处理结果并不是为了得到高分辨距离像,只是作为估计目标运动参数的参考量,所以精度要求并不高。要想得到更为精确的目标一维距离像可以通过其他方法获得[15,17-18]。

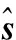
(14)

(15)

式中,hk(v,a)包含全部M′组一维距离像信息。

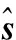
为克服传统参数遍历法运算量大的缺点,本文运用黄金分割法思想[23]进行参数搜索,并将速度、加速度分开进行估计,避免了对速度、加速度熵值二维曲面进行搜索带来的运算量大的问题。另外,对于调频步进信号,速度的估计精度要求较高。为进一步提高估计精度,可以将速度估计分成两步进行。首先对速度进行粗估计;然后进行加速度估计;最后对速度再进行一次精估计,最终得到精确的速度、加速度估计值。

因此,本文基于全局最小熵的随机稀疏调频步进信号运动补偿算法步骤如下。

步骤 1运用全局最小熵包络对齐算法对稀疏回波进行包络对齐,得到M′组脉冲的回波采样数据Su(v,a)。

(16)

(17)

式中

(18)

步骤 5若|v1-v2|>ε,则收缩搜索区间。

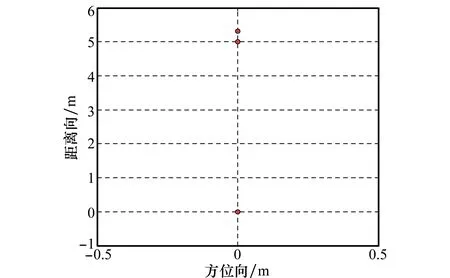
若E(v1)

(19)

若E(v1)>E(v2),则收缩搜索区间如下:

(20)

步骤 6经过K次迭代后,若|v1-v2|≤ε,则终止参数搜索。此时若E(v1)

速度的精估计按照上述过程进行,在此不再赘述。在第二次速度精估计时,由于速度误差已经较小,可以缩小速度搜索范围,减少处理时间。

最终,总结本文算法实现步骤如图2所示。

3　算法性能分析

3.1运算量分析

本文方法包括包络对齐与初相校正两个步骤,下面分别进行分析。

包络对齐阶段:对于全局最小熵包络对齐方法,其计算量主要集中在算法中时、频域转换过程,一般迭代3～7次即可满足估计精度要求[21]。如果忽略运算量较小的加法、乘法运算,算法中只用到了4次傅里叶变换,一次傅里叶变换的运算量为O(Nlog2N),对于整个包络对齐过程运算量为:4PMNO(Nlog2N),P为迭代次数。

初相校正阶段:其主要运算量集中在参数搜索阶段。黄金分割法迭代次数Jv可以用式(21)来计算:

(21)

通常第一次速度搜索范围设置较大,假设速度范围为[-1 000,1 000],精度ε=0.001,则速度迭代次数为30次;第二次速度精估计搜索范围不需很大,通常设置为[-100,100],此时迭代次数为25次。同理加速度估计范围通常设置为[-50,50],迭代次数为Ja=29次。而文献[5,7]中利用的是速度、加速度区间遍历的方法,假设搜索区间及精度要求不变,仅速度区间搜索次数就要达到2×106次,这将消耗大量的处理时间。而本文算法大大缩减了搜索次数,减少了运算时间。

另外,在熵值计算过程中,只有简单的加法、乘法运算,计算量较小。主要运算量同样集中在傅里叶变换过程,一次搜索需进行2M次傅里叶变换,则运算量为O(2MNlog2N)。那么总的运算量为:O(2JvMNlog2N+2JaMNlog2N)。

总的来说,本文提出的随机稀疏调频步进信号运动补偿算法总的运算量为:4PMNO(Nlog2N)+O((Jv+2Ja)2MNlog2N)。可以看出,由于算法中最耗时的运算为傅里叶变换过程,所以本文算法运算量较小。

图2　新方法处理流程示意图

3.2抗噪性能分析

在随机稀疏调频步进信号运动补偿算法中,常规最小熵方法通常利用一个脉冲串进行处理,而本文算法利用的是所有脉冲信息,增加了信噪比积累,适用于低信噪比条件下的运动补偿。具体来看,对于IFFT过程具有N′倍的信噪比积累。由于运动参数估计运用了全局的思想,利用了M′组脉冲,所以具有M′倍信噪比积累。因此相对于常规处理算法,本文算法具有N′M′倍信噪比增益,更加适用于低信噪比条件下的运动补偿。

4　仿真分析与验证

本文所用仿真软件为MatlabR2008b,仿真计算机配置为:处理器为Intel酷睿E7500,主频2.93GHz,内存2GB。首先说明本文稀疏率、信噪比、参数估计误差的定义。

4.1算法性能仿真

假设雷达发射信号为调频步进信号,其参数设置如表1所示。仿真所用模型如图3所示,仿真散射点距离设置为[0,5,5.3]m。对于稀疏率为K(0.2,0.2)的随机稀疏调频步进波形,其包络对齐前后的效果如图4所示。

表1　仿真实验参数

图3　目标模型

仿真结果表明:图4(a)为包络对齐前的效果,存在明显的走动。图4(b)～图4(e)分别为用不同包络对齐算法进行包络对齐后的效果。可以看出,由于相关性遭到破坏,互相关法、最小熵法得到的包络对齐效果较差,Norm1法甚至已经失效,而图4(e)中的全局最小熵法仍然可以完成包络对齐。图4(f)为通过全局最小熵包络对齐后再进行IFFT处理得到的目标一维距离像,由于运动引入的相位项还没有去除,所以一维距离像仍然是发散的,还需进行初相校正。

图4　不同包络对齐方法效果对比

经过包络对齐处理后,利用本文算法估计得到运动参数如表2所示。为便于比较,表中列出了传统最小熵法[3,5]、SAEM方法[8]、复包络相关法[4]、子脉冲包络拟合法[6]的估计结果。其中本文算法速度、加速度遍历区间分别为[-1 000,1 000]、[-100,100],精度ε=0.001。为节约搜索时间,SAEM方法、最小熵法的速度、加速度遍历区间分别设置为[395,405]、[28,32],精度ε=0.01。

从表2可以看出,通过本文算法可以精确的估计出目标的运动参数,子脉冲包络拟合法以及复包络相关法由于不能估计加速运动的目标,所以估计精度不高。SAEM方法虽然可以估计加速度,但是由于信号频率稀疏造成估计结果误差较大。传统最小熵法估计得到的参数精度有明显提高,但是速度估计误差仍然很大。分别用表2估计的运动参数进行初相校正的结果如图5所示，每个点的工作模式和压缩方法的解释同图4。

表2　参数估计结果

注：1) 包络相关代表复包络相关法;

2) 包络拟合代表子脉冲包络拟合法。

图5　初相校正结果对比

仿真结果分析:图5(a)～图5(d)分别为用复包络相关法、子脉冲包络拟合法、SAEM方法、传统最小熵法估计得到的运动参数进行初相校正的结果。与真实的一维距离像比较可以发现,虽然这些方法补偿掉了一维距离像散焦现象,但是一维距离像的走动仍然存在,说明补偿精度不够,其中传统最小熵法补偿后的走动最小,说明校正效果较好。本文算法进行相位校正后得到的结果如图5(e)所示,可以看出补偿后得到目标一维距离像与真实的距离像重合,说明校正效果最好。另外从图5(e)还可以看出,由于信号稀疏,导致一维距离像旁瓣增多,这对于弱小散射点的识别有一定影响。因此,可以在运动补偿后通过其他方法得到更为精确的目标一维距离像[15,18]。

假设其他条件不变,当信号进一步稀疏时(K(0.3,0.5)),各算法的估计结果如表3所示。

表3　参数估计精度结果

注：1) 包络相关代表复包络相关法;

2) 包络拟合代表子脉冲包络拟合法。

从表3的估计结果可以看出,当信号进一步稀疏时,本文算法仍能准确估计出目标的运动参数。最小熵法算法估计精度有所降低,SAEM方法虽然误差较大,但是仍能使用。而复包络相关法、子脉冲包络拟合法已经失去估计性能。因此本文算法对稀疏调频步进信号的补偿效果优于其他几种方法。

4.2信噪比对估计性能影响

假设其他条件不变,当K(0.2,0.2)时,进行100次实验,得到如图6所示的不同SNR条件下本文算法估计速度、加速度参数的误差曲线。

图6　参数估计误差曲线

从图中可以看出:通过本文算法在SNR低至0 dB的条件下,速度估计误差仍能控制在1.3%以下,加速度误差控制在2.5%以内。因此,本文算法在较低的低SNR条件下仍然具有较强的稳健性。

5　结束语

本文针对随机稀疏调频步进信号运动补偿问题,提出了一种基于全局最小熵的运动补偿算法。算法的主要优势为:①可以实现信号稀疏条件下调频步进信号的运动补偿;②在较低信噪比条件下仍然适用;③复杂度低,计算量较小。并从理论和仿真进行了证明。由于该算法基于的是稀疏条件下的一维距离像进行处理,信号频率稀疏必然会对一维距离像造成高旁瓣、主瓣下降等不利影响,所以对于在不同稀疏条件下该算法的可行性将是下一步研究的重点。

[1] Xu H, Wang J, Yuan J, et al. Range-resolution improvement for spaceborne/airborne bistatic synthetic aperture radar using steeped-frequency chirp trains[J].IEEETrans.onSignalProcessing,2015, 9(4):377-386.

[2] Long T, Han Y Q, Mao E K. Digital signal processing of stepped frequency radar[J].ActaAeronauticaetAstronauticaSinica, 2001, 22(S1):16-25. (毛二可, 龙腾, 韩月秋. 频率步进雷达数字信号处理[J].航空学报, 2001, 22(S1):16-22.)

[3] Jiang N Z, Wang M L, Li S H, et al. Compensation methods for stepped frequency radar HRR imaging[J].JournalofElectronics, 1999, 21(5):665-670. (蒋楠稚, 王毛路, 李少洪, 等. 频率步进脉冲距离高分辨一维成像速度补偿分析[J].电子科学学刊, 1999, 21(5):665-670.)

[4] Bao Y X, Ren L X, He P K, et al. Velocity measurement and compensation method based on range profile cross-correlation in stepped-frequency radar[J].SystemsEngineeringandElectronics, 2008, 30(11):2112-2115. (包云霞, 任丽香, 何佩锟, 等. 频率步进雷达距离像互相关测速补偿算法[J].系统工程与电子技术, 2008, 30(11):2112-2115.)

[5] Chen J, Xiao H T, Fan H Q, et al. ISAR imaging of stepped frequency based on image contrast optimization[J].JournalofNationalUniversityofDefenseTechnology,2014,36(1):93-97.(陈杰,肖怀铁,范红旗,等.基于图像对比度最优的频率步进ISAR成像方法[J].国防科技大学学报,2014,36(1):93-97.)

[6] Zhang H Y, Zhang S H, LI Q. A method of ISAR imaging via stepped frequency modulated radar[J].ActaElectronicaSinica, 2007, 35(12):2329-2334.(张焕颖,张守宏,李强.调频步进雷达ISAR成像方法[J].电子学报,2007,35(12):2329-2334.)

[7] Kim K T. Focusing of high range resolution profiles of moving targets using stepped frequency waveforms[J].IETRadar,SonarandNavigation,2010, 4(4):564-575.

[8] Zhang S H, Liu Y X, Li X. Minimum entropy based ISAR motion compensation with low SNR[C]∥Proc.oftheIEEEChinaSummit&InternationalConferenceonSignal&InformationProcessing,2013:593-596.

[9] Huang W T, Zhou J J, Lu R. Implementation of motion compensation algorithm of HRRP based on TMS320C6678[J].JournalofDataAcquisitionandProcessing, 2014, 29(4):92-99. (黄文韬, 周建江, 路冉. 基于多核DSP的高分辨距离像运动补偿算法实现[J].数据采集与处理, 2014, 29(4):92-99.)

[10] Wang X D. Target imaging and velocity measurement simultaneously algorithm based on step frequency waveforms[J].JournalofSichuanOrdnance, 2015, (5):115-118. (王晓东. 基于步进频率的目标成像与速度精确测量方法[J].四川兵工学报, 2015(5):115-118.)

[11] Niu T, Chen W D. A new method of motion compensation for pulse stepped frequency radars[J].JournalofUniversityofScienceandTechnologyofChina,2005, 35(2):161-166.(牛涛,陈卫东.脉冲步进频率雷达的一种运动补偿新方法[J].中国科学技术大学学报,2005,35(2):161-166.)

[12] Liu Z, Zhang S H. Estimation of target motion parameter in a stepped frequency pulses radar[J].ActaElectronicaSinica, 2000, 28(3):43-45,12. (刘峥, 张守宏. 步进频率雷达目标的运动参数估计[J].电子学报, 2000, 28(3):43-45, 12.)

[13] Zhou Y B, Zhou J J. The high resolution range profile imaging algorithm of the stepped frequency radar based on the second velocity estimation[J].JournalofSignalProcessing, 2013, 29(2):188-193. (周玉冰, 周建江. 步进频率雷达基于二次速度估计的高分辨距离像成像算法[J].信号处理,2013, 29(2):188-193.)

[14] Zhang J D, Gu C, Li Y S, et al. A new method of motion compensation for positive and negative stepped-frequency radar[J].ModernRadar,2009,31(2):36-39.(张劲东,顾陈,李玉晟,等.正负步进频率雷达的运动补偿新方法[J].现代雷达,2009,31(2):36-39.)

[15] Gu F F, Zhang Q, Lou H, et al. A SAR imaging method with sparse aperture and frequency using stepped-frequency waveform[J].ActaAeronauticaetAstronauticaSinica, 2015, 36(4):1221-1229. (顾福飞, 张群, 娄昊, 等. 一种孔径和频率二维稀疏的步进频SAR成像方法[J].航空学报, 2015, 36(4):1221-1229.)

[16] Pang B, Dai D, Xing S, et al. Imaging enhancement of stepped frequency radar using the sparse reconstruction technique[J].ProgressinElectromagneticsResearch,2013,140(1):63-89.

[17] Gu F F, Zhang Q, Lou H, et al. Two-dimensional sparse synthetic aperture radar imaging method with stepped-frequency waveform[J].JournalofAppliedRemoteSensing,2015, 9(1):96099.

[18] Yang J G, Thompson J, Huang X T, et al. Random-frequency SAR imaging based on compressed sensing[J].IEEETrans.onGeoscienceandRemoteSensing, 2013,51(2):983-994.

[19] Xu D, Du L, Liu H, et al. Compressive sensing of stepped-frequency radar based on transfer learning[J].IEEETrans.onSignalProcessing, 2015, 63(12):3076-3087.

[20] Long T, Mao E K, He P K. Analysis and processing of modulated frequency stepped radar signal[J].ActaEletronicaSinica, 1998, 12(12):84-88. (龙腾, 毛二可, 何佩琨. 调频步进雷达信号分析与处理[J].电子学报, 1998, 12(12):84-88.)

[21] Zhu D Y, Wang L, Yu Y S, et al. Robust ISAR range alignment via minimizing the entropy of the average range profile[J].IEEEGeoscienceandRemoteSensingLetters, 2009, 6(2):204-208.

[22] Stankovic L, Stankovic S, Amin M. Missing samples analysis in signals for applications toL-estimation and compressive sensing[J].IEEETrans.onSignalProcessing,2014,94(1):401-408.

[23] Ni Q.Optimizationmethodandprogramdesign[M]. Beijing: Science Press, 2009: 17-18. (倪勤. 最优化方法与程序设计[M]. 北京:科学出版社, 2009: 17-18.)

Motion-compensation method based on global minimum entropy for random sparse stepped-frequency chirp signal

LÜ Ming-jiu1, LI Shao-dong1, YANG Jun2, MA Xiao-yan2

(1. Department of Graduate Management, Air Force Early Warning Academy, Wuhan 430019, China;2. Air Force Early Warning Academy, Wuhan 430019, China)

When the transmitting waveform is stepped-frequency chirp signal with randomly sparse frequency and aperture, it can not only reduce the requirement of the sampling rate, but also improve the anti-jamming ability. However, the disadvantage is that it is difficult to make the motion compensation. A motion compensation method based on global minimum entropy is proposed. Firstly, we use the global minimum entropy method to complete the envelope alignment. Secondly, we convert the problem of initial phase correction into the problem of parameter estimation of radial velocity and acceleration. In order to obtain high estimation precision of the velocity, we combine the rough searching and precise estimation together, taking the global minimum entropy as the cost function, and search with variable step lengths based on the golden-section method, then, the parameter estimation method becomes fast and highly precise. Theoretical analysis and simulation results show that the proposed algorithm has the advantages of fast calculation speed, high estimation accuracy and high robustness under low SNR conditions.

randomly sparse stepped-frequency chirp signal; motion compensation; golden-section method; global minimum entropy; one-dimension range profile

2015-10-12；

2016-02-17；网络优先出版日期：2016-05-03。

TN 957

A

10.3969/j.issn.1001-506X.2016.08.06

吕明久(1985-),男,博士研究生,主要研究方向为目标检测与识别技术。

E-mail:lv_mingjiu@163.com

李少东(1987-),男,博士研究生,主要研究方向为压缩感知在雷达成像中的应用。

E-mail:liying198798@126.com

杨军(1973-),男,副教授,博士,主要研究方向为雷达系统、雷达信号处理与检测理论。

E-mail:yangjem@sina.com

马晓岩(1962-),男,教授,博士,主要研究方向为雷达系统、雷达信号处理与检测理论、现代信号处理及其应用。

E-mail:mxyldxy@sina.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160503.1024.006.html