基于改进NCS算法的弹载FMCW SAR大斜视成像方法
梁 颖, 张 群, 杨 秋, 顾福飞, 何彦杰
(1. 空军工程大学信息与导航学院, 陕西 西安 710077;2. 中国人民解放军95980部队, 湖北 襄阳 441100)
基于改进NCS算法的弹载FMCW SAR大斜视成像方法
梁颖1,2, 张群1, 杨秋1, 顾福飞1, 何彦杰2
(1. 空军工程大学信息与导航学院, 陕西 西安 710077;2. 中国人民解放军95980部队, 湖北 襄阳 441100)
调频连续波(frequency modulated continuous wave,FMCW)合成孔径雷达(synthetic aperture radar,SAR)具有体积小、重量轻、成本低、功耗低等优点,在精确制导领域具有较大的应用潜力。推导分析了弹载FMCW SAR大斜视回波信号波数域表达式,在成像预处理中,通过引入全时间距离走动校正函数,有效避免了由导弹高速运动及大斜视角观测引起的二次相位误差的产生;在方位向处理中,给出了一种改进的非线性调频变标算法(nonlinear chirp scaling,NCS),补偿了方位空变相位误差,实现了方位向的高精度成像。最后仿真实验验证了理论分析结果及所提成像方法的有效性。
调频连续波; 合成孔径雷达; 大斜视成像; 改进的非线性调频变标
0 引 言
弹载合成孔径雷达(synthetic aperture radar, SAR)主要是为实现导弹精确制导的目的,是继电视、红外和激光成像制导技术之后又一重要的成像制导技术[1]。其全天时、全天候工作等优点使其成为目前精确制导领域一个重要的发展方向。然而,传统的脉冲式SAR由于工作体制的原因,通常体积、重量和功耗较大,不适合应用于小型化的导弹平台。而调频连续波(frequency modulated continuous wave, FMCW) SAR具有体积小、重量轻、成本低、功耗低等优点[1-6],在精确制导领域具有较大的应用潜力。
弹载SAR大斜视成像可对前方目标预先成像,在精确制导及精确打击中发挥着重要的作用,是弹载SAR系统必不可少的工作模式之一。因此将FMCW SAR系统应用于导弹平台,研究基于FMCW信号体制的弹载SAR大斜视成像方法具有重要的军事意义[7-10]。
由于FMCW SAR信号体制及接收方式的不同,已有的关于脉冲式SAR的大斜视成像方法不能直接应用于FMCW SAR中。进而有相应改进的FMCW SAR大斜视成像算法的提出,如改进的距离多普勒(range Doppler, RD)算法[10-11]、改进的频率变标(frequency scaling, FS)算法[12-13,16]、改进的波数域算法[14-15]以及改进的非线性调频变标(nonlinear chirp scaling, NCS)算法[16-17]等。
大斜视成像的观测模式会在距离向引入一个线性走动分量,导致距离向产生距离走动,在成像预处理中需进行距离走动的校正,而距离走动校正处理同时会带来方位空变的问题,直接对方位向进行匹配滤波处理将导致方位向成像质量下降。针对上述问题,文献[16]提出了一种斜视等效正侧视的成像处理方法,该方法在方位向处理中采用NCS算法,克服了方位聚焦深度的限制;文献[17]对目标斜距表达式进行3阶展开,采用基于级数反演的方法求解回波信号的多普勒频域表达式,并在多普勒频域完成3次相位的补偿,在方位向处理中,同样采用NCS算法,克服方位空变性导致的聚焦深度的限制。但是,这些算法均未考虑平台高速运动对回波信号的影响。同时,所采用的NCS算法未考虑3阶以上的方位空变相位误差对成像的影响,当方位向分辨率较高时,3阶方位空变相位误差同样会对方位向聚焦产生影响。
论文在现有成像算法的基础上,针对弹载FMCW SAR平台的特点,提出了一种基于改进NCS算法的弹载FMCW SAR大斜视成像方法。首先,在成像预处理中通过引入全时间距离走动校正函数进行距离走动校正,有效避免了由导弹高速运动及大斜视角观测引入的二次相位误差的产生;在方位向处理中,考虑3阶空变相位误差对成像的影响,给出了一种改进的NCS算法,补偿了方位空变性引起的高阶空变相位误差。
1 回波信号模型
弹载FMCW SAR大斜视成像几何模型如图1所示,雷达工作在条带模式,斜视角为θ0,导弹飞行高度为h,平台运动速度为v,R0为波束中心线扫过目标时的中心斜距。

图1 弹载FMCW SAR大斜视成像几何模型
FMCW SAR成像中通常需考虑导弹飞行过程中与目标之间距离的脉内变化。因此,场景中目标点与导弹之间的瞬时斜距可表示为
(1)
式中
(2)
式中,δ(tk)为关于快时间tk的幂级数,该项将导致回波信号中产生多普勒频移和二次相位误差,在后续的处理中需对该项进行补偿。将R(tm)在tm=Xn/v处进行泰勒级数展开,并保留到3次项,即
(3)
弹载FMCWSAR在大斜视工作模式下,回波信号经“dechirp”处理后的波数域表达式为[18]
(4)
式中,RΔ=R(tk,tm)-Rref,Rref为参考距离。ΔKR=4πμtk/c;KRc=4πfc/c;KR=4πfc/c+4πμtk/c=KRc+ΔKR;b=8πμ/c2;⊗为卷积符号。最后一个指数项为剩余视频相位(residualvideophase,RVP)项,在后续的处理中可将其忽略。
2 成像方法
2.1成像预处理
通常在大斜视成像模式下回波信号会存在一个线性走动分量,该线性走动分量会引起距离向的距离走动,对距离走动的校正,可通过构造统一的补偿函数对其进行补偿。考虑弹载FMCWSAR大斜视成像的特点,构造全时间距离走动校正函数为
(5)
式中,X′=X+vtk,X=vtm。将式(5)与式(4)相乘,得到距离走动校正后的回波差频信号表达式为
(6)
通过引入全时间距离走动校正函数进行距离走动校正后,回波差频信号进行方位向傅里叶变换,转换到二维波数域为
(7)
式中,KX=2πfa/v,fa为多普勒频率。作变量代换X′=X+vtk后,式(7)可进一步表示为
(8)
根据驻相点法解式(8)的积分,得回波差频信号的二维波数域表示形式为
(9)
式中,KC=4πμ/c。第1个指数项包含了FMCWSAR二维成像的相位因子,具体表达式为
(10)
式中,第1个指数项为方位向成像因子;第2个指数项为雷达平台连续运动引起的多普勒频移相位项,多普勒频移项将导致距离像频谱偏移及方位像散焦。文献[11]中关于弹载FMCWSAR大斜视成像方法研究中指出,导弹的高速运动与大斜视角成像会引入一个二次相位误差,影响距离成像成像。二次相位误差主要是由距离走动校正引起的,通过上述分析,全时间距离走动校正函数的引入,有效地避免了二次相位误差的产生,无需再进行二次相位误差的补偿。需要指出的是,对于一般的机载FMCWSAR大斜视成像方法,平台运动速度通常较低,二次相位误差对成像的影响完全可以忽略,因此在距离走动校正函数的构造中无需构造文中提及的全时间距离走动校正函数。
对导弹平台连续运动引起的多普勒频移进行校正,多普勒频移校正函数为
(11)
经上述补偿后,回波差频信号二维波数域表示形式为
(12)
2.2距离向处理
对式(9)中的相位Φ在ΔKR=0处进行泰勒级数展开,并保留到2次项,即
(13)
式中
Φ1、Φ2为引起距离弯曲的两个相位项,分别构造距离弯曲和二次距离压缩补偿函数对其进行补偿,补偿函数分别为
(14)
(15)
经补偿后回波差频信号的二维波数域表达式为
(16)
对式(16)进行距离向的傅里叶逆变换,得
(17)
至此,便完成了距离向的处理。
2.2方位向处理
式(17)中的Φ0为方位向成像因子,因此,在方位向处理中主要针对该项进行处理。将Φ0在KX=0处进行泰勒级数展开,得
(18)
式中,Ka=-2KRccos2θ0/R0为多普勒调频率;Ks=sinθ0/KRccos2θ0,第1项对方位向成像没有影响,在后续的处理中可将其忽略。由于距离走动校正函数的引入,导致方位多普勒调频率随方位位置的不同而变化,令Rs=R0+Xnsinθ0,则目标点方位位置为Xn的多普勒调频率可进一步表示为
(19)
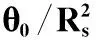

图2 方位向三阶空变相位误差曲线
采用非线性调频变标的思想,构造4次相位滤波函数:
(20)
将式(17)与式(20)相乘后进行方位向傅里叶逆变换,采用级数反演的方法[20]求解相乘后的表达式为
(21)
此处省略了式(17)中与方位向处理无关的第2项。构造方位非线性调频变标函数为
(22)
将式(22)与式(21)相乘后进行方位向傅里叶变换,同样采用级数反演的方法求解相乘后的二维波数域表达式为
(23)
将式(23)中的相位整理为关于KX和Xn的级数,即
(24)
式中
(25)
(26)
(27)
(28)
(29)
(30)
为了补偿空变相位误差,需按照式(25)~式(30)选择合适的q2,q3,q4,p3和p4。因此,式(25)~式(30)应满足:φ1=-1/β,φ3=φ4=φ5=0。β为变标因子,一般取接近于1且大于1的值。求解联立的方程组可得
(31)
经非线性调频变标处理后,式(23)进一步表示为
(32)
然后进行方位脉压处理,方位匹配函数为
(33)
经方位匹配滤波处理后获得目标二维图像。在算法运算性能方面,方位向处理中给出的改进NCS算法,充分考虑高阶空变相位误差对成像的影响,能够进一步提高方位向成像精度;同时整个算法流程只是提高了相应的滤波函数和变标函数的构造精度,并未增加额外的运算量,且不存在插值运算,能够满足弹载SAR对实时成像处理的需求。
3 仿真验证与分析
仿真参数如表1所示,场景中心坐标(单位:km)为(25,15,0),3个目标点的坐标(单位:km)分别为A(24,15,0),B(25,15,0),C(26,0,15)。图3分别给出了采用RD算法[10]、NCS算法[17]及本文算法时A点成像结果及剖面图对比。

表1 仿真参数
在成像预处理中,本文通过引入全时间距离走动校正函数进行距离走动校正,有效避免了二次相位误差的产生。如采用传统的距离走动校正方法,将会引入二次相位误差,导致距离像主瓣展宽,旁瓣电平抬高。由距离向剖面图对比可以看出,采用NCS算法获得的距离像峰值旁瓣比(peak side lobe ratio, PSLR)和积分旁瓣比(integrated side lobe ratio, ISLR)分别为-7.24 dB和-6.10 dB,而采用本文算法获得的距离像PSLR和ISLR分别为-12.99 dB和-9.49 dB。
在方位向处理中,本文给出的改进NCS算法进行了3阶空变相位误差的补偿,与RD算法及NCS算法相比,能够更好地完成方位向的聚焦。RD算法由于未考虑空变相位误差的影响,已无法完成方位向的聚焦,而NCS算法由于只进行了2阶空变相位误差的补偿,方位像仍存在一定的散焦及旁瓣不对称的现象。采用NCS算法获得的方位像PSLR和ISLR分别为-8.08 dB和-6.23 dB,而采用本文算法获得的方位像PSLR和ISLR分别为-12.97 dB和-9.54 dB。
图4为采用本文所提方法,A、B、C3个点的二维等高线图,成像质量如表2所示。由此可知,本文所提弹载FMCW SAR 大斜视成像方法能够获得较好的成像结果。

图3 A点成像结果对比

图4 点目标成像结果

目标点距离向PSLR/dBISLR/dB方位向PSLR/dBISLR/dBA-12.99-9.49-12.97-9.54B-13.22-9.53-12.71-9.31C-13.16-9.62-12.48-9.34
4 结 论
FMCW SAR由于其自身的优越性,必将在精确制导领域受到越来越广泛的关注。本文对弹载FMCW SAR大斜视成像方法展开研究,提出了一种基于改进NCS算法的弹载FMCW SAR大斜视成像方法。在成像预处理中通过引入全时间距离走动校正函数,有效避免了二次相位误差的产生;在方位向处理中,给出一种改进NCS算法,通过提高相应的滤波函数及变标函数的构造精度,获得了较好的方位向成像结果。理论分析和仿真实验表明,该方法能够获得较好的目标二维像,能够为FMCW SAR系统应用于精确制导领域提供一定的参考。
[1] Zhu M B, Yang L B, Yang R L.Missile-borneSARguidance:fundamentalsandkeytechniques[M]. Beijing: National Befense Industry Press, 2014: 1-5. (祝明波, 杨立波, 杨汝良. 弹载合成孔径雷达制导及其关键技术[M]. 北京: 国防工业出版社, 2014: 1-5.)
[2] Meta A, Hoogeboom P. Development of signal processing algorithms for high resolution airborne millimeter wave FMCW SAR[C]∥Proc.oftheIEEEInternationalRadarConference, 2005: 326-331.
[3] Meta A, Hoogeboom P, Ligthart L P. Signal processing for FMCW SAR[J].IEEETrans.onGeoscienceandRemoteSensing, 2007, 45(11):3519-3532.
[4] Lanari R. A new method for the compensation of the SAR range cell migration based on the chirp Z-transform[J].IEEETrans.onGeoscienceandRemoteSensing, 1995, 33(5):1296-1299.
[5] Wang R, Luo Y H, Deng Y K, et al. Motion compensation for high-resolution automobile FMCW SAR[J].IEEEGeoscienceandRemoteSensingLetters, 2013, 10(5):1157-1161.
[6] Edrich M. Ultra-light weight synthetic aperture radar based on a 35 GHz FMCW sensor concept and online raw data transmission[J].IEEProceedings-RadarSonarNavigation,2006,153(2):129-134.
[7] Jaeschke T, Bredendiek C, Pohl N. 3D FMCW SAR imaging based on a 240 GHz SiGe transceiver chip with integrated antennas[C]∥Proc.oftheGermanMicrowaveConference, 2014:10-12.
[8] Ribalta A. Time-domain reconstruction algorithms for FMCW-SAR[J].IEEEGeoscienceandRemoteSensingLetters, 2011, 8(3):396-400.
[9] Zhou S, Zhou P, Zhang L, et al. Imaging of missile-borne SAR based on FMCW[J].SystemsEngineeringandElectronics, 2011, 33(10):2203-2209. (周松, 周鹏, 张磊,等. 调频连续波弹载SAR成像方法[J].系统工程与电子技术, 2011, 33(10):2203-2209.)
[10] Liang Y, Wang H X, Xing M D, et al. Imaging study of high squint SAR based on FMCW[J].JournalofElectronics&InformationTechnology,2009,31(4):776-780.(梁毅,王虹现,邢孟道,等.基于FMCW的大斜视SAR成像研究[J].电子与信息学报,2009,31(4):776-780.)
[11] Liang Y, Zhang Q, Yang Q, et al. Study on the high squint imaging method for missile-borne FMCW SAR[J].ChineseJournalofRadioScience, 2014, 29(6):1115-1121. (梁颖, 张群, 杨秋, 等. 弹载调频连续波合成孔径雷达大斜视成像方法研究[J].电波科学学报, 2014, 29(6):1115-1121.)
[12] Jiang Z H, Huang F K. Squint LFMCW SAR data processing using Doppler-centroid-dependent frequency scaling algorithm[J].IEEETrans.onGeoscienceandRemoteSensing,2008,46(11):3535-3543.
[13] Li D, Liao G X, Yang Z W, et al. Frequency scaling algorithm for high squint FMCW-SAR imaging[J].JournalofXidianUniversity, 2013, 40(4):21-28. (李东, 廖桂生, 杨志伟,等. 用于大斜视FMCW-SAR成像的频率变标算法[J].西安电子科技大学学报(自然科学版), 2013, 40(4):21-28.)
[14] Wang R, Loffeld O, Nies H, et al. Focus FMCW SAR data using the wave number domain algorithm[J].IEEETrans.onGeoscienceandRemoteSensing, 2010, 48(4):2109-2118.
[15] Ma B Q, Zhang D W, Wang Y F. A wavenumber domain algorithm using four-order polynomial interpolation for squint FMCW-SAR[J].ModernRadar,2014,36(2):47-51.(马兵强, 张大炜, 王岩飞. 斜视FMCW-SAR的四阶多项式插值波数域算法[J].现代雷达, 2014, 36(2):47-51.)
[16] Liang Y, Guo L, Xing M D, et al. An equivalent side-looking method for squint FMCW SAR[J].ActaElectronicaSinica, 2009, 37(6):1159-1164.(梁毅,郭亮,邢孟道,等.一种斜视FMCW SAR的等效正侧视处理方法[J].电子学报,2009,37(6):1159-1164.)
[17] Zhang S X, Li J, Zhang L, et al. Frequency modulated continuous wave squint synthetic aperture radar imaging algorithm based on series reversion[J].ActaElectronicaSinica, 2013, 41(3):532-538. (张双喜, 李军, 张磊,等. 基于级数反演的斜视FMCW SAR成像算法研究[J].电子学报, 2013, 41(3):532-538.)
[18] Bao Z, Xing M D, Wang T.Radarimagingtechniques[M]. Beijing: Publishing House Electronics Industry, 2005:165-168. (保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005:165-168.)
[19] An D X, Huang X T, Jin T, et al. Extended nonlinear chirp scaling algorithm for high-resolution highly squint SAR data focusing[J].IEEETrans.onGeoscienceandRemoteSensing, 2012,50(9):3595-3609.
[20] Zhou P, Zhou S, Xiong T, et al. A chirp-Z transform imaging algorithm for missile-borne SAR with diving maneuver based on the method of series reversion[J].JournalofElectronics&InformationTechnology,2010,32(12):2861-2867.(周鹏,周松,熊涛,等.基于级数反演的弹载SAR下降段CZT成像算法[J].电子与信息学报,2010,32(12):2861-2867.)
Study on the high squint imaging method for missile-borne FMCW SAR based on extended NCS algorithm
LIANG Ying1,2, ZHANG Qun1, YANG Qiu1, GU Fu-fei1, He yan-jie2
(1. Institute of Information and Navigation, Air Force Engineering University, Xi’an 710077, China)(2. Unit 95980 of PLA, Xiangyang 441100, China)
The frequency modulated continuous wave (FMCW) synthetic aperture radar (SAR) has the properties of compact size, lightweight, low cost and low power dissipation, which provides great potential in the application of precision guidance. The return signal expression in the wave number domain is deduced and analysed. In the imaging preprocessing, the quadratic phase error which is induced by the high speed and high squint angle is not generated, according to the inducing of the all-time range walk correction function. In the azimuth processing, an extended nonlinear chirp scaling algorithm is proposed. The azimuth-variance phase error is compensated, and a high precise azimuth imaging is achieved. Finally, some results are given for validating the theoretical derivation and the effectiveness of the proposed method.
frequency modulated continuous wave (FMCW); synthetic aperture radar (SAR); high squint imaging; extended nonlinear chirp scaling (NCS) algorithm
2015-03-25;
2015-09-23;网络优先出版日期:2016-04-19。
国家自然科学基金(61172169);空军工程大学优秀博士学位论文基金(KGD 081014004)资助课题
TN 95
A
10.3969/j.issn.1001-506X.2016.08.09
梁颖(1986-),男,工程师,博士,主要研究方向为雷达信号处理。
E-mail:liangying8633@163.com
张群(1964-),男,教授,博士,主要研究方向为雷达信号处理与目标识别。
E-mail:zhangqunnus@gmail.com
杨秋(1986-),男,工程师,博士,主要研究方向为雷达信号处理。
E-mail:yangqiu1105@163.com
顾福飞(1987-),男,工程师,博士,主要研究方向为雷达信号处理与信息传输技术。
E-mail:gffpan@126.com
何彦杰(1987-),男,工程师,硕士,主要研究方向为雷达系统与装备保障。
E-mail:yanjiehe311@163.com
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160419.1506.002.html

