具有等距密排微小孔穿刺模板的力学分析

赵世海，王婷慧，董九志，蒋秀明（1.天津工业大学 机械工程学院，天津 300387；2.天津工业大学 现代机电装备技术天津市重点实验室，天津 300387）



具有等距密排微小孔穿刺模板的力学分析

赵世海1，2，王婷慧1，2，董九志1，2，蒋秀明1，2
（1.天津工业大学 机械工程学院，天津 300387；2.天津工业大学 现代机电装备技术天津市重点实验室，天津 300387）

穿刺模板用于正交叠层碳布织机中，其上开有近千个紧密排列的微孔使得力学分析较为困难.首先根据拟板理论用2种方法求出了等效弹性模量：一种是从细观层次出发由渐进均匀化理论得出；另一种是从宏观角度应用薄板理论，分别得出了剩余弹性模量和孔密度的关系图.然后根据工程需要利用拟板求出了穿刺模板的等效板厚和自振频率.最后设计了实验以测试理论分析所得的关系图，综合2种理论方法和实验所得的3个结果找出了在不同孔密度区间里求等效弹性模量的最优方法.

穿刺模板；等距密排微小孔；均匀化理论；等效弹性模量；拟板理论；力学分析

modulus；pseudo-plates theory；mechanical analysis

等距密排穿刺模板在碳布的整体穿刺工艺中用于制造碳纤维立体织物［1］.碳纤维立体织物是高性能碳纤维在三维空间多方向连续排布形成的纤维增强体.整体穿刺的过程是将钢针放置成Z向钢针阵列，固定于工作台上，碳布置于穿刺模板下方，在穿刺模板带动下穿过Z向钢针阵列，重复上述过程直到满足所需厚度，使用Z向纤维置换Z向钢针，制成立体织物.

在整体穿刺过程中穿刺模板向下移动，接触静止的碳布后，带动碳布一同穿过静置的Z向钢针阵列，当碳布与钢针阵列接触时开始穿刺过程，钢针对碳布有作用力，导致碳布变形，与此同时，碳布对穿刺模板的微小孔边产生力的作用.

在此过程中穿刺模板起到为钢针定位和给碳布加压的作用，随着碳布层数的增加，碳纤维立体织物的厚度加大，钢针在穿刺中承受较大的反作用力后会倾斜、弯曲甚至折断，穿刺模板的微小孔约束了钢针的上述运动；另外，由于各层碳布是否密实直接影响立体织物的力学性能，这时穿刺模板起到了加压的作用.因此，穿刺模板必须有足够的刚度，以保证在整个穿刺过程中发生尽可能小的弯曲变形.由于开孔对板的弯曲刚度影响很大，含有近千个微小孔的穿刺模板和加工板所用的材料相比，其弯曲刚度大为削弱.

穿刺模板的外部尺寸符合薄板弯曲理论的条件，但是利用ANSYS直接建模分析时会出现2个障碍导致分析中止：一是由于孔很小，应力和挠度以及其它变形分量等一些物理量随位置变化呈现震荡特征，使得力学分析过程复杂且结果不可靠；二是如果直接应用有限元进行数值模拟，划分网格时由于每个微孔的四周都有孔，每个孔的圆周上至少要分4个节点。穿刺模板上孔的数目多，描述该类结构需要很密的网格从而形成很多单元，穿刺模板上有近千个孔使得上述计算量巨大，超出微型计算机的计算能力，导致无法求解或者求解精度过低.

穿刺模板的结构特点是在板的中心区域按照一定规律开了很多孔，孔径比板的轮廓尺寸小得多.本文采用拟板理论，把穿刺模板的微小孔抹去，用同尺寸的实心板代替穿刺模板，由此可知代替穿刺模板完成力学分析的等效实心板与穿刺模板应该有同样的弹性常数，以保证等效实心板和穿刺模板在受到相同的激励载荷时响应相同.

1　穿刺模板的力学分析

图1表示了穿刺模板的细部结构.由图1可以看出，穿刺模板的结构特点是紧密排列的微孔中心距相等，排布显周期性特征.

图1　穿刺模板结构模型Fig.1　Structure model of piercing template

本文先根据拟板理论把密排孔板的孔抹去使其等价为另一种材料制成的实心板，也就与是密排孔板等价的拟板，在不改变板的形状和尺寸的条件下求出拟板的弹性模量定义为密排孔板的等效弹性模量［2］.借鉴复合材料板的分析方法，用细观和宏观2种方法求出2组等效弹性模量［3-4］.

细观方法应用基于小参数摄动法的渐进均匀化理论和有限元分析的理论［5］.先根据细观力学中的代表单元法划分出单胞，然后将单胞的应力应变以及应变位移的关系式代入虚功方程，将位移展开为含小参数的渐进表达式后代入上述方程，利用周期性性质和散度定理化简方程得出等效弹性模量的张量表达式；最后利用通用有限元分析的格式将张量式改写为矩阵方程，求出刚度矩阵从而得到等效弹性模量［6］.

根据结构的周期性划分出的代表单元称为单胞，理想单胞可以通过空间上无重叠、无缝隙的延拓即可重现真实的密排孔板结构并且要有规则的几何外形.此外如果单胞外廓闭合，则在二维坐标系中是单连通域，有利于物理方程的化简中直接应用高斯散度定理.基于以上原因穿刺模板的单胞模型如图2所示［7］.

图2　单胞模型Fig.2　Model of base cell

建立2个尺度的坐标系，宏观用X表示，细观用Y表示.引入小量，其物理意义是把宏观坐标系X中的一个点放大倍放入细观坐标系Y中，建立了一个模型在宏观和细观上对应关系.穿刺模板在垂直于板中面的方向孔的形状和尺寸沿厚度不变，在弹性力学中可归结为的平面问题处理并且密排孔板的弹性矩阵设为正交各向异性材料的形式，可知待求量为E11、E12、E22和E66.

经数学推导得出等效弹性模量的表达式

宏观方法是基于经典薄板理论，以密排孔板和拟板受相同的外载荷时的最大挠度相等为条件建立方程，从中提出抗弯刚度的关系式从而得到等效弹性模量［9］.又由于等效前后板的外形尺寸不能变，所以微孔数目越多，板的实体部分的体积相应就越小，每个小孔周边承受的载荷就越大，这就建立起孔的数量和弹性模量的关系.综上可得Timoshenko理论，其中正方形薄板的中心挠度的精确值为

2　案例分析

密排孔板的外形尺寸为20 cm×20 cm，等距密排孔区域面积为256 cm2，厚度为1 cm.有976个微孔，孔径为4 mm，孔边间距1 mm.密排孔板的弹性模量为210×106Pa，泊松比μ=0.3，密度为7.85×103kg/m3，表面受压力载荷为4×104N/m2.用MAPLE解有限元矩阵的结果为：

由观察结果可知，在板上的微孔是圆形且等距排列时，密排孔板的弹性矩阵显各向同性材料的特征.

另一种解法是由上文推出的边界条件直接用ANSYS建单胞模型［10］.为了保证单胞的变形协调还需再加上周期性边界条件，即保证单胞外边界相对的2个面的所有点的位移变化一致［11］.具体实施的方法是在WORKBENCH中用“强迫位移”命令添加位移约束. 图3为单胞水平方向有一个单位初应变的变形，剩余2种情况类似.

图3　单胞变形图Fig.3　Deformation of base cell

ANSYS与MAPLE给出的结果相差无几，原因是2种方法本质是一样的，只是同一个矩阵方程用2种计算器求解而已.用MAPLE的解是先借助ANSYS APDL划分网格，导出此时节点和单元信息然后导入MAPLE，用ANSYS求解是建模、划分网格、加载边界条件全程借助ANSYS的模块，优点是可以借助ANSYS强大的后处理器得到直观的变形图像.

从宏观角度来看板的中心挠度就是最大挠度故取密排孔板中心区域的小样［12］.令密排孔板的中心挠度为w，弹性模量E，拟板的中心挠度为wH弹性模量EH.借助ANSYS APDL建立小样模型，求出w和w′再代入（3）求出.用同样的方法能求出不同开孔直径下的［13］.

由于最终要得出开孔数量对板的弹性模量的削弱程度，故定义剩余弹性模量为EH/E，其中分母为加工密排孔板所用材料的弹性模量.开孔数量用孔密度表示，定义为α等于孔板的体积和当量板体积比值.2种方法求出的剩余弹性模量和孔密度的关系如图4所示.

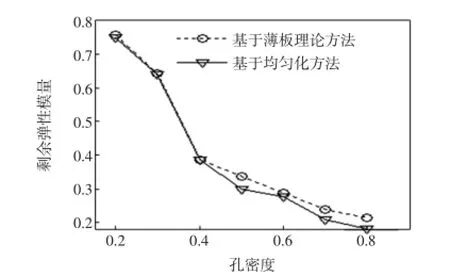
图4　剩余弹性模量-孔密度图Fig.4　Residual modulus of elasticity-density of hole

观察图4得出2条结论：一是当板上的微孔是圆形、等距排列且在孔密度小于0.4时，细观方法和宏观方法数值相近，可以推测出按此方法分析时最佳孔密度为0.3到0.4，但是随着孔的数量增多，计算所得剩余弹性模量数值的离散度增加，到底哪种更接近实际由后续试验验证；另一个是可以根据曲线拟合原理得出α和的关系式接近指数函数形式

式中：x、y和z为待定常数.

3　拟板的应用

在应用拟板理论求出等效弹性模量的过程中要求拟实心板和密排孔板的外形尺寸一致，以保证两者在承受相同的外载荷时把密排孔对刚度的削弱表现在弹性模量上.如果把原密排孔板和拟板都看由2种无关的材料制成的实心板，当两板的表面积一样时就把密排孔对刚度的削弱表现为厚度的折减，求出拟板的厚度值称为等效板厚.

根据克希霍夫-泰勒假设，选取中面挠度为基本未知量，另外2个位移分量是中面挠度的函数，在直角坐标系中弯曲微分方程为

式中：q为垂直于中面的外载.

根据中面的定义，计算出中面位置h1

此时的抗弯刚度Dh1计算公式变为

下面推导计算等效板厚的公式，目的是在已知密排孔板的材料的情况下，快速判断出相当于多厚的实心板.要说明的是等效板厚公式的前提：孔为圆形，正方形，正六边形等规则几何轮廓；每个孔的中心距一样，显正三角形或正方形排列，目的是保证能利用各向同性板的理论；厚度方向孔的尺寸不变化.如果存在阶梯孔可以根据厚度方向的不同孔径分段处理，由于以上所有推导都是在小挠度线弹性的前提下进行，可以把分段处理的结果直接相加得到整个板的等效厚度.

建立方程的依据是保证两者在相同外载荷下的相同变形，把密排孔对刚度的削弱表现为厚度的折减.厚度H由弯曲刚度表征，所以直接令两者的弯曲刚度相等即可求出等效厚度HH，H为密排孔板的实际厚度.

借助ANSYS得到原厚度为10 mm的穿刺模板相当于厚度为5.71 mm的实心板.

穿刺时模板在随工作台上下往复运动，这种工况下通常需求出穿固有频率.借助ANSYS的模态组块，可以求出任意阶的自振频率，用拟板建模从后处理器可提取的各阶频率的数值和图形，得到的一阶自振频率即密排孔板的固有频率.

4　剩余弹性模量的验证试验

在理论分析中宏观和细观2种方法的操作中必须用有限元方法离散，解的精确性和节点的数量、网格的形状及单元的选取密切相关，故在理论分析后设计了试验测试图4得出剩余弹性模量和孔密度的关系.实验设备为天津工业大学机械学院材料力学实验室的WDW3100微机控制电子万能试验机.

至今为止没有针对具有密排孔结构的板的拉伸试验标准，本次试验的试样参照国家标准中短比例薄板试样的规范，取试样的总长度为200mm，标距为50 mm.根据理论分析的结果可知对于薄板可忽略厚度对剩余弹性模量影响，考虑到试样的拉断时间和加工方便，直接从2 mm厚的钢板取样.由于密排孔区域强度削弱较大，故试样在拉伸过程中一定是在密孔区域而不会在夹持部分屈服，故没有设计夹持过度段，断裂后的试样也验证了这点.

表1列出了本次试验的4种试样.

表1中，0号试样是未开孔板，目的是测出剩余弹性模量中分母的数值.1、2、3号试样分别测出开孔密度为0.2、0.3、0.6时的等效弹性模量的值.其中1号和3号试样的孔为等距排布，2号试样的孔为横纵向中心距不相等的情况.受加工条件的制约2和3号试样没能做到孔密度严格一致，但是相近的孔密度也能反映出孔的排布方式对剩余弹性模量的影响程度，而且以横纵向距离不相等的试样做反向对照，为进一步分析不等距的密排孔板的提供实验数据.同样受加工条件的限制本次试验的试样最大孔密度取到60%，表2为实验数据.

表1　试样规格明细Tab.1　 Specification list of sample

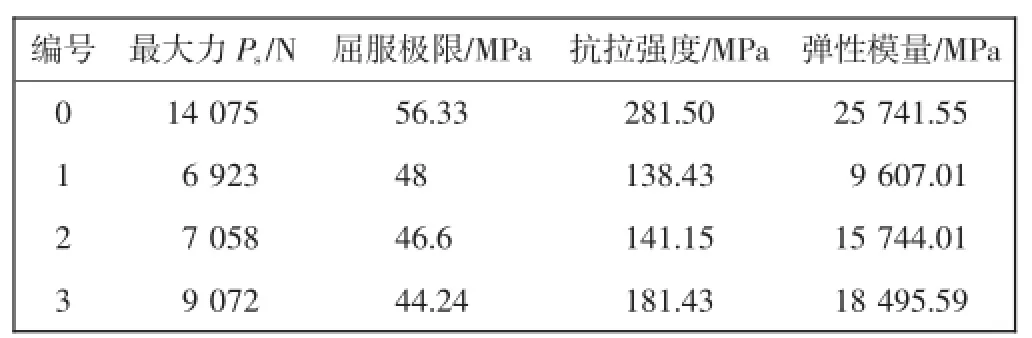
表2　实验结果Tab.2　Experimental data

每种试样都取3件做试验，表2的结果是3件试样的算术平均值.屈服力是按照惯例取0.2%的残余变形时的值.0号试样测出了剩余弹性模量中分母的值，其余试样的弹性模量都和其相比.1号试样的剩余弹性模量的实验值为0.37，理论值为0.297，2号试样的实验值为0.612，理论值为0.65，3号试样的实验值为0.718，理论值为0.74.分析实验数据可以直接看出2点：一是当开孔密度低于0.6时，用宏观薄板理论和细观均匀化方法求出的理论值和实验值吻合的较好，但随开孔密度孔的增加数值的离散度加大，本次试验的数据更接近薄板理论的分析结果，可见均匀化方法的结果更趋于保守；二是像2号试样这样每排孔的中心距统一变化时，孔间距对剩余弹性模量的影响不大.因为虽然2号试样把纵向的孔距增大，按照开孔率的计算公式板上有孔处的总面积也随之加大，降低了开孔率，并且整排孔的变动数值一样时结果类似于等距的情况.

观察试样的断裂位置发现同一规格的三件试样的断裂位置不一样，即并非都发生在中间一排，并且2号试样在相邻两排孔都有断裂，1号和3号试样断裂虽然不一定发生在哪一排，但都是同一排孔统一短.由此可以看出改变孔间距虽然对剩余弹性模量的影响不大，但对板的破坏形式有影响.同时可以推测出断裂发生在孔间距的加工误差较大的位置，那么随孔密度加大，加工误差影响成为导致实际值的离散度加大的重要因素.

图5为未开孔试样的实验力-位移曲线，图6为孔密度为0.6的曲线，结合其他试样的曲线图可以发现，随着孔密度的增大密排孔结构试样的曲线没有明显的弹性阶段、屈服阶段、强化阶段的分界区间.

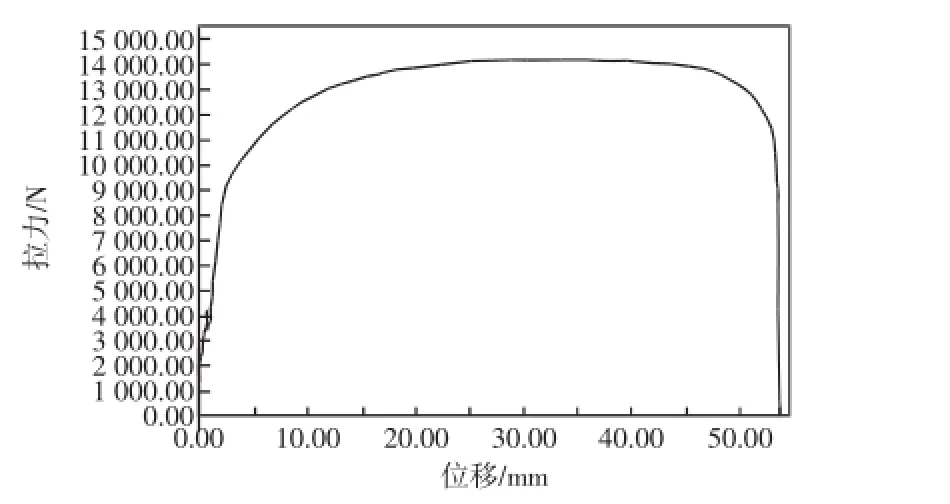
图5　0号试样的实验力-位移曲线Fig.5　Experimental force displacement curve of sample 0

图6　1号试样的实验力-位移曲线Fig.6　Experimental force displacement curve of sample 1

5　结语

具有等距密排微小孔的穿刺模板的力学分析不能直接用有限元方法仿真，本文用拟板理论，用模拟出的实心板分析密排孔板的一些力学指标.为了保证结果的可靠性，用细观均匀化方法和薄板理论求出了等效弹性模量并得出了几种不同规格的开孔数量对弹性模量弱度，即剩余弹性模量-孔密度曲线；随后列举了拟板的两个用途；最后设计了试验测试理论分析的结果，发现由细观均匀化方法求出的数值均稍微低于实验所得，说明此方法所得数据更可靠.

需要指出的是，这种模拟的实心板不是在任何情况都能代替密排孔板，比如在强度分析中由于孔的存在会造成局部的应力集中，在疲劳破坏分析中冲击载荷作用时某些边缘区域的孔会先出现破坏.同时实验表明加工精度对密排孔板力学性能影响很大，例如板的某些边缘区域孔间距如果有很小的误差，受弯曲外载荷时破坏失效很可能就发生于此，这些用模拟的实心板都难以得出.

［1］朱建勋，何建敏，王海燕.正交叠层机布整体穿刺工艺的纤维弯曲伸长机理［J］.中国工程科学，2003，5（5）：59-62.

ZHU J X，HE J M，WANG H Y.Fiber elongation mechanism orthogonal bending laminated cloth overall puncture process［J］. Engineering Sciences，2003，5（5）：59-62（in Chinese）.

［2］谢桂兰，赵锦枭，田杰，等.均匀化有限元法预测复合材料层合板宏观有效弹性性能 ［J］.玻璃钢/复合材料，2014（7）：23-27（in Chinese）.

XIE G L，ZHAO J X，TIAN J，et al.Predicting macroscopic effective elastic properties of composite laminated plate by homogenization fem［J］.Fiber Reinforced Plastics/Composites，2014（7）：23-27（in Chinese）.

［3］杜修力，金浏.细观均匀化方法预测非饱和混凝土宏观力学性质［J］.水利学报，2013，47（3）：355-371.

DU X L，JIN L.Micro-scale homogenization for prediction of the mechanical properties of unsaturated concrete［J］.Journal of Hydraulic Engineering，2013，47（3）：355-371（in Chinese）.

［4］TERADA K，KATO J，HIRAYAMA H，et al.A method of two-scale analysis with micro-macro decoupling scheme：Application to hyperelastic composite materials［J］.Comput Mech，2013，52：1199-1219.

［5］HASSANI B，HINTON E.A Review of homogenization and topology optimization I-homogenization theory for media with periodic structures［J］.Computers and Structures，1998（69）：707-717.

［6］DAVALOS-SOTELO Raymundo.Determination of elastic properties of clear wood by the homogenization method in two dimensions［J］.Wood Sci Technol，2005，39：385-417.

［7］董纪伟，孙良新，洪平.基于均匀化方法的三维编织复合材料等效弹性性能预测［J］.宇航学报，2003，26（4）：482-486.

DONG J W，SUN L G，HONG P.Homogenization-based method for predicting effective elastic properties of three-dimensional braided composites［J］.Journal of Asronautics，2003，26（4）：482-486（in Chinese）.

［8］ HASSANI B，HINTON E.A review of homogenization and topology optimization II-analytical and numerical solution of homogenization equations［J］.Computers and Structures，1998 （69）：719-738.

［9］伍莉，刘均，程远胜.方形蜂窝夹芯夹层板弯曲问题的新解法［J］.船舶力学，2012（8）：926-934.

WU L，LIU J，CHENG Y S.A new algorithm for solving being response of square-honeycomb sandwich plates［J］.CSSRC Reports，2012（8）：926-934（in Chinese）.

［10］刘洋，何斌，傅洁，等.周期变截面梁刚度分析的均匀化方法［J］.机械设计与制造，2014（1）：21-24

LIU Y，HE B，FU J，et al.Stiffness analysis of the periodic variablecross-sectionbeambasedonhomogenizationmethod［J］. Machinery Design&Manufacture，2014（1）：21-24（in Chinese）.

［11］刘远，金国光，刘又午，等.基于有限段方法的高速凸轮机构动力学分析［J］.天津工业大学学报，2007，26（6）：66-69.

LlU Y，JIN G G，LIU Y W，et al.Dynamic analysis of highspeed cam mechanisms based on finite-segment method［J］. Journal of Tianjin Polytechnic University，2007，26（6）：66-69 （in Chinese）.

［12］王珂，刘彤，董其伍.复杂多孔板有效弹性常数的结构分析方法［J］.压力容器，2010，27（5）：10-14.

WANG K，LIU T，DONG Q W.Strucual analysis methods to determine the effective elastic constants for perforated plates［J］. Pressure Vessel Technology，2010，27（5）：10-14（in Chinese）.

［13］周亮，唐予远，聂建斌.多胞织物结构复合材料静态弯曲性能与有限元分析［J］.天津工业大学学报，2008，27（5）：4-7.

ZHOU L，TANG Y Y，NIE J B.Experimental and FEM calculation of 3-D glass/polyester resin cellular woven composite under quasistatic three-point bending［J］.Journal of Tianjin Polytechnic University，2008，27（5）：4-7（in Chinese）.

Mechanical analysis of piercing template with equal center distance and closely aligned tiny hole

ZHAO Shi-hai1，2，WANG Ting-hui1，2，DONG Jiu-zhi1，2，JIANG Xiu-ming1，2
（1.School of Mechanical Engineering，Tianjin Polytechnic University，Tianjin 300387，China；2.Tianjin City Key Laboratory of Modern Mechatronics Equipment Technology，Tianjin Polytechnic University，Tianjin 300387，China）

Piercing template is used in the integrated piercing process of orthogonal laminated woven fabrics.There are nearly a thousand closely aligned small holes，which make it difficult to analyze the mechanical behavior.The effective modulus was obtained from the pseudo-plates theory from two aspects，that is，homogenization theory and elastic theory，respectively.And the characteristics of each method are discussed.According to the engineering requirement，the equivalent plate thickness and the natural frequency were calculated by using the isoeffective modulus.

piercing template；equal center distance and closely aligned tiny hole；homogenization theory；isoeffective

TH112

A

1671－024X（2016）03－0073－05

10.3969/j.issn.1671-024x.2016.03.014

2015-12-15

天津市科技支撑重点计划项目（15ZCZDGX00840）

赵世海（1970—），男，博士，副教授，主要研究方向为新型纺织机械设计.E-mai：tjshzhao@163.com