基于多目标规划的GNSS地面站任务资源优化

徐伯健，李昌哲，卜德锋，符京杨

(1.北京卫星导航中心，北京 100094；2.西安测绘总站，陕西 西安 710054；3.中国洛阳电子装备试验中心，河南 洛阳 471003)



基于多目标规划的GNSS地面站任务资源优化

徐伯健1，李昌哲2，卜德锋3，符京杨1

(1.北京卫星导航中心，北京 100094；2.西安测绘总站，陕西 西安 710054；3.中国洛阳电子装备试验中心，河南 洛阳 471003)

摘要随着卫星导航系统的不断建设和发展，在复杂任务、多空间和长时间等多约束条件下的导航卫星地面站的资源优化分配问题逐渐显现。为了准确、高效地解决该问题，应用多目标数学规划对导航卫星地面站的任务资源建立相关模型并进行求解，仿真结果表明，建立模型的稳定度评价值量化指标在0.2以内，优于常用模型。因此，该方法可以成为尝试解决导航卫星地面站资源优化问题的一种手段，为未来卫星导航系统形成全球覆盖能力、多地面站执行复杂任务时的资源优化分配问题的研究打下了基础。

关键词导航卫星地面站；资源优化；多目标规划

0引言

2020年前后，全球卫星导航系统(GNSS)的规模将比现阶段有更大提升，导航卫星地面站的监测任务量也会大大增加。因此，对目前导航卫星地面站有限的业务资源及管理资源的优化分配的重要性逐渐突显出来。针对相应的导航任务，得出可适用于多目标的资源优化方案，合理、有效地分配导航卫星地面站有限的业务资源，并在任务期内应对资源冲突时给出多组应对方案并进行比较择优，以支持多导航任务同时进行。该问题已成为拥有自主GNSS系统的国家的学者们逐渐涉猎的研究方向。资源优化问题的难度与任务相关的因素和其他约束条件同数学模型有着紧密的联系。

在理论研究层面，目前许多学者对卫星地面站任务规划及资源调度的算法开展了广泛研究。通过建立基于单任务的多约束数学模型，并采用贪婪算法[1-2]、混合蚁群算法[3]和模拟退火算法[4]等进行求解，有效地解决了卫星地面站单任务优化问题。该类模型算法的优点是可以获得模型的最优解且易于编程实现，存在的问题是难以处理复杂的约束条件以及随机性约束，进而难以应用于处理真实的地面站优化问题。在应用研究层面，目前已在地震电磁卫星[5]、电子侦查卫星[6]和星地混合网络[7]的应用中取得一定进展。文献[8-9]提出了相应的模型，文献[10-11]对卫星地面站的能力进行了分析与评估。目前现有的研究主要针对通信和遥感卫星，而GNSS系统具有卫星数量多、星座构成复杂的特点，现有文献对其地面站任务资源优化研究较少，故应开展相关研究。

1导航卫星地面站任务资源优化分析

目前我国导航卫星地面站的业务资源及管理资源相对有限，而这些有限的资源又是维持卫星导航系统正常运行的必备基础之一，也就是说卫星导航系统的地面控制段业务都由这些导航地面站业务资源来保证。每一个地面站都有共同任务和独特任务，而每一个任务在特定的时间和空间需要有特定的任务资源来支撑。此外，还需要考虑任务持续的时间。

通过前面的基础描述，可以理解卫星导航的任务方案必须由资源分配方案作为基础，卫星地面站的资源优化分配方案都不能在任意的时空范围上超过其资源承载能力。目前已有人针对卫通系统提出了关键设备资源调度思想[12]。而卫星导航任务是多目标任务，需要将多种因素纳入考虑，多目标数学规划可能有多样的可行解，那么具体选择哪个，要根据任务的需求和地面站的时空条件等要素予以全局考虑。整个多目标规划的目的是要最大化有效任务—资源连接的数目，最终得到最优的资源分配方案。

2导航卫星地面站任务资源优化的数学模型

导航卫星地面站任务资源优化的数学模型其核心与多目标数学规划最优解的性质相同，而多目标数学规划问题的标准形式[13]如下：

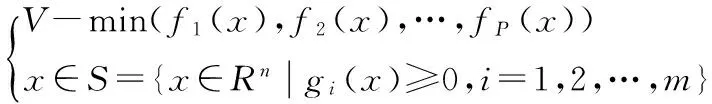
式中，V-min表示对P个目标函数f1(x),f2(x),…,fP(x)以向量(f1(x),f2(x),…,fP(x))形式来评价方案的好坏，以区别于单目标规划中求最小的符号min。

这样就在卫星导航地面站任务资源优化建模时统一了模型的数学概念。

多目标规划问题最显著的应用特点是可以用来评价多个目标评价方案的好坏。对一个多目标规划问题，在约束集合S中，如果存在一个方案x*对每个目标都是最优的，则称这个解x*为该多目标规划问题的绝对最优解。但是在实际遇到的问题中，绝对最优解往往是不存在的。既然绝对最优解往往不存在，所面临的问题就是对2个或多个都不是绝对最优解的方案，比如x(1),x(2)进行比较，区分其好坏。为了叙述方便，令

F(x)=(f1(x),f2(x),…,fP(x))，

对每个x∈S,F(x)是P维空间RP上的一个向量。x(1),x(2)所对应的目标向量分别是：

F(1)=F(x(1))=(f1(x(1)),f2(x(1)),…,fp(x(1)))，

F(2)=F(x(2))=(f1(x(2)),f2(x(2)),…,fp(x(2)))。

要比较x(1),x(2)的好坏，就要比较这2个目标向量F(x(1)),F(x(2))的好坏，但是比较2个向量的好坏是困难的。为此，要通过软件程序进行计算比较。

3导航卫星地面站任务资源优化方案

3.1程序实现的流程

如上所述，导航卫星地面站任务资源优化的多目标任务规划数学模型建立以后，可以通过ILOG OPL组件[14]来解算模型，从而得到任务资源优化的可行解，应用程序对其实现的流程如图1所示。

3.1.1定义决策变量

决策变量也叫做控制变量。用符合目标的适当数值来描述系统的任务特性，其数量称之为自由度，该值不能多于总的变量数和方程数目的差值。

在对所描述的问题确定后，定义导航卫星地面站(Station)站名(name)、地面站编号(sta_id)和信号传输设备数(Num)，描述如下：

Station=。

可选择项(Alternative)含任务资源编号(taskres_id)、地面站编号(sta_id)、初始时间(FTime)、持续时间(duration)和结束时间(LTime)，描述如下：

Alternative=。

以上2个公式完成了决策变量的定义。

图 1　程序实现流程

3.1.2定义优化目标

优化目标是指导航卫星地面站任务资源与相关因素的函数关系。根据多目标规划数学模型中的描述，优化目标应为最大化的导航卫星与地面站任务资源中相关的数目，描述如下：

max{sum{a|ai≠aj;a,ai,aj∈Alternatives,}}。

3.1.3定义约束条件

运用多目标规划的数学方法解决导航卫星地面站任务资源优化问题时，需将必须明确的前提条件定义为多目标任务规划的约束条件。约束条件的选择往往受到多目标规划中的多重条件的限制。

在导航卫星地面站任务资源优化问题中主要需满足的约束条件，首先是任务资源必须被使用且满足任务完成的基本条件，

task∈Tasks&{task,ta1,ta2∈Alternative;ta1≠ta2}。

另外一个关键的约束条件是导航卫星地面站的最大任务资源量不能超过站点所能承受的极限资源量s.Max，表达式为：

∑{task∈A&s∈S&task.sta_id=s.sta_id}<=s.Max。

3.2解决方案的生成

最终应用ILOG OPL组件进行求解，生成的结果便是导航卫星地面站任务资源优化方案的一组解，使得结果与任务资源的需求量相对应，在执行过程中设定上限并充分满足任务的时间节点，其中模型中所含的过程量也可在生成结果中查询到，最终可得数据解及多组解的比较结果，如图2所示。

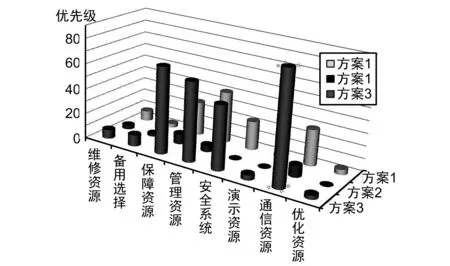
图2　导航卫星地面站任务资源优化解决方案对比

3.3仿真实验与分析

针对GNSS地面站任务资源优化案例进行仿真，仿真条件如下：实验在Windows7(64位)系统，Intel CORE i7处理器，8 GB内存储器，仿真软件选用ILOG OPL和Matlab R2015b的工作站上进行。地面站位置模拟位置位于北纬N37°0′0″，东经E113°30′0″，高程为1 089.66 m。在目前已有的GNSS系统中选择GPS系统为仿真实验研究对象，星历采用IGS提供的精密星历数据。设定任务资源优化以300个历元时刻为周期重复进行，则任务中存在的冲突主要体现在每个周期内地面站中存在的任务对资源的竞争。由于该时刻卫星可见数目可知，可以确定目标活动的资源预约用量值，因此可以确定导航卫星与地面站之间的时间窗口，从而应用模型进行资源优化。

首先根据地面站资源优化问题的特点及其特定性，将资源优化的求解共分3个阶段：系统初始配置阶段、初始化阶段和冲突检测与修复阶段。在系统初始配置阶段，主要获得参数的输入，包括地面站参数的定义和任务与资源的声明；在初始化阶段，对具体的计算模型进行迭代计算生成一个初始化结果，初始化并不可得到优化结果，结果中可能存在很多冲突；冲突检测与修复阶段负责对初始化结果中的冲突进行探测和修复，本文实验中设计了一个循环修复算法，通过反复的冲突修复最终生成一个满足优化目标的输出结果。资源优化求解流程如图3所示。

在资源优化的初始化解的过程中，本文参考文献[2]和文献[4]中提出的模型，将其抽象为单任务多约束的模型1和模型2，并与本文提出的模型进行比较。通过对ILOG OPL给出的3种方案进行迭代计算，从而对评价值进行考核。该评价值表示经过模型优化过的平均值与计算结果的平均值的比值，理论上越接近于1表示该模型更加优化和稳定，如表1所示。

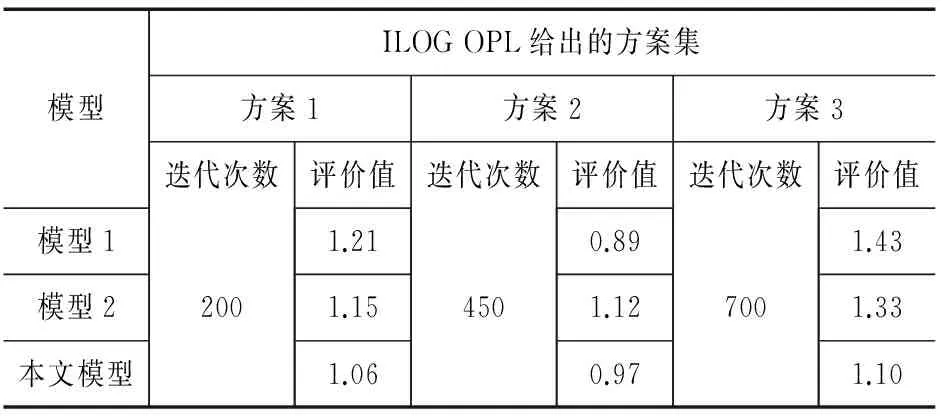
表1　3种模型应用于各方案的评价值比较

此外，针对评价值的考量还应验证其随时间变化的稳定度。3种模型随时间变化的评价值如图4所示。从图4中可以看出，本文采用的模型在程序运行5 min的计算时间内，相比模型1和模型2的评价值浮动较小，证明本文采用的模型在稳定度方面具有一定优势。

图4　3种模型随时间变化的评价值

3.4结论

通过对上述实验结果加以分析和归纳，可得结论如下：

① 基于多目标数学规划的模型可以尝试建立导航卫星地面站的任务资源优化模型；

② 应用该模型的数学解得到的方案可以形成现有的导航卫星地面站任务资源管理方案的备选方案集；

③ 相比单任务多约束的数学模型及其解法，采用多目标数学规划法建立模型可以得到更加综合稳定的优化解。

4结束语

本文对导航卫星地面站任务资源优化问题进行了描述，针对该问题建立了数学模型，并提出了通过确定相关决策变量、约束条件和目标函数，进而尝试采用ILOG OPL软件对问题演算和求解。

在未来的研究中，应结合我国自主的GNSS地面站管理任务，形成更切合实际情况且更为精确的基于多目标任务规划的资源优化数学模型并进行求解，同时尝试应用更多的现有程序与ILOG OPL组件进行接口集成，使得导航卫星地面站的任务资源优化问题拥有更多、更好、更快的解决方案。

参考文献

[1]张超.基于贪婪算法的遥感地面站任务调度技术[J].无线电工程,2011,41(1):58-60.

[2]张红旗.基于贪婪算法的卫星地面站资源调度方法[J].无线电工程,2010,40(12):4-6.

[3]邢立宁,陈英武.基于混合蚁群优化的卫星地面站系统任务调度方法[J].自动化学报,2008(4):414-418.

[4]韩丽,张学庆.基于模拟退火的卫星地面站任务规划方法[J].无线电工程,2010,40(9):42-43.

[5]王红飞,刘玉荣,阎镇.地震电磁卫星任务规划系统研究[J].空间科学学报,2010,30(6):620-625.

[6]冉承新,熊纲要,王慧林,等.电子侦察卫星任务规划调度模型与算法研究[J].通信对抗,2009(1):3-8.

[7]徐婧婧.星地混合网络中的容量规划与任务调度研究[D].成都:电子科技大学,2013.

[8]徐露露,陈俊,冯钟葵,等.一种卫星地面系统中实现任务调度策略可配置的方法[J].遥感信息,2012,27(6):35-38.

[9]金光.卫星地面站测控资源调度CSP模型[J].系统工程与电子技术,2007(7):1 117-1 120.

[10]金光,武小悦,高卫斌.基于冲突的卫星地面站系统资源调度与能力分析[J].小型微型计算机系统,2007(2):310-312.

[11]常飞.卫星地面站系统资源能力评估方法研究[D].长沙：国防科学技术大学,2005.

[12]孟学军,赵艳朝,林贺.卫星通信地球站智能切换单元的设计与实现[J].无线电通信技术,2014,40(5):89-92.

[13]陈庆华，郭全魁.装备运筹学教程[M].北京:国防工业出版社,2006.

[14]杨广强.基于ILOG OPL的传输网资源使用能效优化分析[J].现代电信科技,2011,41(7):54-57.

doi:10.3969/j.issn.1003-3106.2016.07.12

收稿日期：2016-03-15

中图分类号V556.1

文献标志码A

文章编号1003-3106(2016)07-0045-04

作者简介

徐伯健男，(1973—)，高级工程师。主要研究方向：卫星导航定位性能提升。

Optimization of GNSS Ground Station Task Resources Based on Multi-objective Programming

XU Bo-jian1,LI Chang-zhe2,BU De-feng3,FU Jing-yang1

(1.TheBeijingSatelliteNavigationCenter,Beijing100094,China;2.Xi’anDivisionofSurveyingandMapping,Xi’anShaanxi710054,China;3.LuoyangElectronicEquipmentTestingCenter,LuoyangHe’nan471003,China)

AbstractWith the continuous construction and development of satellite navigation system,the problem of resource allocation of navigation satellite ground station is gradually emerging in constraints of complex tasks,multi space,and long time.In order to solve this problem accurately and efficiently,the task resource of navigation satellite ground station is established by using multi-objective mathematical programming.The simulation results show that the stability evaluation value of the model is less than 0.2,which is better than the common model.This method can solve the problem of the optimization of the ground station resources,and it is the basis of studying the resource optimization allocation for complex tasks implementation through multiple ground stations when the future satellite navigation system has global coverage capability.

Key wordsGNSS ground station;resource optimization;multi-objective programming

引用格式：徐伯健,李昌哲,卜德锋,等.基于多目标规划的GNSS地面站任务资源优化[J].无线电工程,2016,46(7):45-48.