混凝土简支梁桥动荷载时程分析

鲁亚斌, 王　亮

(山东科技大学土木工程与建筑学院，山东青岛 266590)



混凝土简支梁桥动荷载时程分析

鲁亚斌, 王亮

(山东科技大学土木工程与建筑学院，山东青岛 266590)

【摘要】在混凝土桥梁的设计中，桥梁的抗震设计占据了整个设计过程的一大部分，同时也是桥梁在使用过程中能否满足长期性能的关键因素。文章通过对跨径为30 m的简支混凝土梁桥在动荷载作用下的跨中挠度和弯矩的研究，说明车辆的行驶速度对动荷载在梁桥上作用产生的位移和弯矩的影响。采用迈达斯(Midas)建立模型的方法进行模拟研究，分别考虑了车速为10 km/h、20 km/h、40 km/h、80 km/h以及120 km/h时的荷载时程，分析了相关因素下的桥梁弯矩和位移。研究结果表明车辆的行驶速度越大，桥梁的动力效应越大，即对桥梁的影响也越大。

【关键词】简支梁桥；时程分析；车速；位移；弯矩

1理论研究方法

时程分析(Time History Analysis)是对受动力荷载的结构通过动力方程式进行求解的过程，即根据结构本身的特性和所受的荷载来分析在任意时刻结构的反应，如位移、内力等。时程分析方法可分为直接积分法(Direct Integration)、振型叠加法(Moda Superposition)和静力法(Static Force)。

直接积分法(Direct Integration)就是将时间作为积分参数解动力方程式的方法，又称为时域逐步积分法。直接积分法的优点是可以考虑刚度和阻尼的非线性特点，计算相对准确，但是因为要对所有时间步骤都要积分，所以分析时间相对较长。

静力法是使用动力分析方法模拟Pushover分析(静力弹塑性分析)的方法，也可以用于确定静力荷载作用下(使用时变静力荷载方法)结构的铰状态。之所以称为静力法，是因为求解过程中忽略了动力方程中的加速度和速度项，而位移和荷载项也没有了真正意义上的时间概念，只有荷载控制和位移控制中的步骤概念。时程分析中的静力法与Pushover分析相比其优点是:

(1)可控制正反两个方向上的位移，这样更接近于实际地震的振动(Pushover分析的位移是单方向的)。

(2)用户定义铰特性值更自由，并且可通过定义纤维截面更详细地确认截面内破坏情况。

振型叠加法是将多自由度体系的动力反应问题转化为一系列单自由度体系的反应，然后再线性叠加的方法。其优点是计算速度快、节省时间，但是由于采用了线性叠加原理，原则上仅适用于分析线弹性问题。当进行非线性动力分析时或者因为装有特殊的阻尼器而不能满足阻尼正交(刚度和质量的线性组合)时是不能使用振型叠加法的。

本论文采用的就是振型叠加法来进行的模拟计算。因为简支梁桥可以近似的模拟为线弹性问题，其刚度和质量符合线性组合，而且该方法计算速度较快可以大大节省时间。

本文所用的桥梁模型为跨径30 m的混凝土简支桥梁，其横截面的尺寸和桥梁的荷载数据见图1。使用迈达斯(Midas)模拟过程以单位动荷载为例，因为以单位荷载为例更具备代表性，在此过程中不论最终的车辆总轴重为多少，都可以在定义节点动力荷载时，调整其中的系数来达到目的[1]。

图1　桥梁尺寸模型示意

当施加荷载时，由于车辆荷载作用在节点时是个瞬间作用后随即消失的一种冲击荷载， 所以在这里将其近似地模拟为最大值为1 kN的三角形荷载，其中时间t1和t2间的时间差由车辆的速度和所建模型的节点间距来决定(图2)。

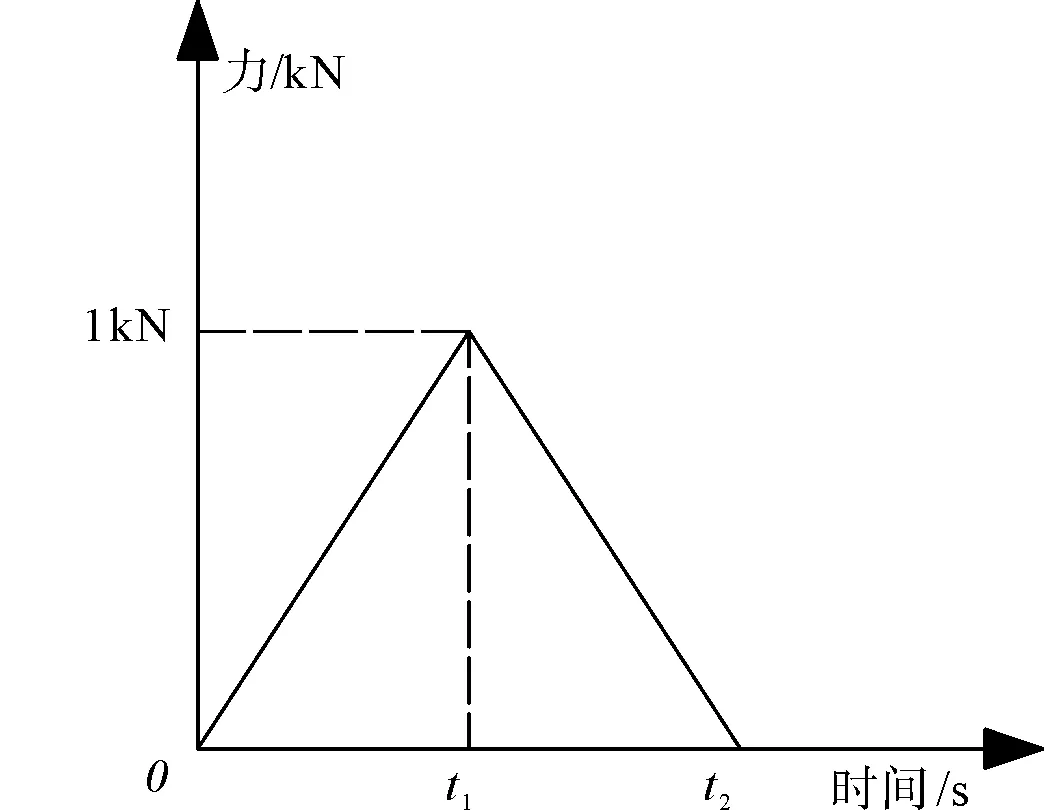
图2　车辆荷载的近似模拟

2迈达斯(Midas)建模模拟分析

2.1特征值分析

结果的精确性可以通过增加频率数量来提高，但所需的分析时间会很长，而且高阶模态对结构的动力反应的影响不是很大，所以在这里本次模拟考虑到第8个模态，之后查看其振型质量参与系数。时程分析中所输入的分析时间步长对分析结果影响很大，一般将分析时间步长设为最高阶振型周期的1/10比较合适。因此，尽管时程分析与特征值分析可以同时进行，但为了查看最高阶振型的周期和振型参与系数以此来确保模拟结果的精确，还是应进行特征值分析。

振型叠加法的时程分析是基于特征值分析的基础上的， 所以需先查看特征值分析的结果。另外如前所述，还需查看最高阶振型的周期以便设定分析时间步长。由模拟结果的特征值分析结果可知，模态8的自振周期为0.009 783 s，则分析时间步长为：

Δt=Tp/10=0.009783/10=0.0009783≈0.001

故可近似地将分析时间步长设为0.001 s。

为获得桥梁结构的动力反应的主要特征，桥梁的振型参与质量需达到总质量的90%以上[2]，本模型的模拟结果表明到模态8为止的振型参与质量的合计为96.42%(图3)。因此可以判断，对于竖直方向的反应，所参与的质量已经足够可以获得结构动力反应的主要特征。

图3　振型参与质量统计图示

2.2荷载时程分析

为了凸显最后的模拟结果，在定义施加节点动荷载时，将参与系数放大10倍，即相当于在桥梁上施加的力为10 kN。设定的荷载是从第二个节点开始的，节点动力荷载如图4所示。

图4　节点动力荷载布置

在分析总时间上，为了考虑车辆通过桥梁后的动力效应，一般时间要大于车辆通过桥梁的时间。时程分析的分析时间步长对结果的精确度影响很大，分析时间步长的大小与结构的高阶模态的周期和荷载的周期有密切的关系。车辆荷载作为一种冲击荷载，它的周期很难确定，因此在这里如前所述考虑结构的高阶模态的周期来决定分析时间步长，即分析的时间步长为0.001 s。

在进行结构的振型时程分析时，结构的阻尼比也是一个重要的因素，对于混凝土结构，它们的阻尼比为0.05～0.10，故这里取0.05作为此结构的阻尼比。

时程分析的结果在本文只考虑跨中挠度和弯矩的时程曲线，经模拟后的时程曲线(车速为120 km/h)包括位移(跨中挠度)和跨中弯矩曲线，如图5、图6所示。

图5　车速为120 km/h的位移时程曲线

图6　车速为120 km/h的弯矩时程曲线

由图5、图6可知，车速为120 km/h时，简支梁桥的跨中最大挠度为6.272 mm，发生在0.444 s；跨中弯矩为95.13 kN·m，发生在0.437 s。为便于分析，现将车辆通过桥梁的速度为10 km/h、20 km/h、40 km/h、80 km/h以及120 km/h时的时程结果统计列于表1。车速不同则车辆荷载作用在各节点的时间会发生变化，因此需要在时程荷载函数对话框中修改时间间距，并在时程荷载工况对话框中修改分析时间总长。另外在节点动力荷载中还需根据车速调整到达时间。

表1　不同车速车辆动荷载时程统计

3简支梁桥静力分析

3.1跨中挠度的计算

目前计算车辆荷载作用下的桥梁的挠度值，都是把桥上的车辆荷载化为等代荷载，计算等代荷载引起的跨中弯矩，再用均布荷载作用下的简支梁跨中挠度计算公式进行计算[3]。

由上式可知，当简支梁桥上只有一个集中荷载作用时，其跨中挠度的计算公式为：

在计算桥梁的动力效应时，一般要考虑车辆过桥是对桥梁产生的冲击影响，而冲击影响一般都是用静力学的方法，即将车辆荷载作用的动力影响用车辆的重力乘以冲击系数来表达。因此在计算动力效应时就必须考虑其冲击系数。冲击系数的取用按内插法计算，当桥梁计算跨径为5 m时，冲击系数1+μ取1.0；当计算跨径为45 m时，冲击系数1+μ取1.3。对于本计算模型，冲击系数μ的取值按下式计算[4]：

因此，当考虑汽车过桥时对桥梁结构产生的竖向动力效应时，跨中挠度的大小为：

f1=(1+μ)·f0=5.058mm

3.2跨中弯矩的计算

当简支梁桥仅受集中力作用时，跨中弯矩的大小按下式计算，即:

当考虑冲击效应时，跨中弯矩的大小按下式计算，即:

M=(1+μ)M0=1.1125×75=83.44kN·m

4静力分析与时程分析结果比较

为便于对比分析，现将时程分析结果和静力分析结果统计列于表2。

表2　静力分析和时程分析结果统计

由表2可知,由于车速的变化，结构产生了动力效应,且时程分析后的结果要大于其考虑冲击系数后的静力分析结果。车速越大产生的动力效应也就越大，当车速为10 km/h时跨中的最大位移为4.537 mm，与静力分析的结果4.496 mm很接近，但随着车速增加，动力反应逐渐明显，最大位移也逐渐加大了。当车速达到120 km/h时，其最大位移较之考虑冲击系数时的位移大24.01%，弯矩较之考虑冲击系数时的弯矩大14.01%。当然，由于本模型是将车辆荷载近似模拟成了一个集中荷载的形式，因此与实际情况存在一些差异。

5结论

当车辆通过桥梁时，会对桥梁产生一定的动力效应，且此效应随着车辆通过桥梁的速度的增加而增大。当车辆以较高的速度通过桥梁时，极其容易对桥梁产生较大的损害。因此在进行桥梁的抗震设计时，应该将通过桥梁的车辆速度作为一个参考因素,而在后期进行桥梁的运营和养护时，也应该限制车辆的行驶速度,只有这样才可以保证桥梁的使用寿命。

参考文献

[1]邱顺冬.桥梁工程软件midas civil应用工程实例[M].北京: 人民交通出版社， 2011.

[2]GB 50011-2010 建筑抗震设计规范[S].

[3]李永珠.简支梁桥挠度计算方法的探讨[J].华东公路，1991, 73(6): 48-49.

[4]姚玲森.桥梁工程[M].2版.人民交通出版社, 2010.

[作者简介]鲁亚斌(1989～),男,硕士研究生，从事道路与桥梁方向研究。

【中图分类号】U441+.3

【文献标志码】A

[定稿日期]2015-12-24