基于GIXRR反射率曲线的二氧化硅纳米薄膜厚度计算

马一博，王梅玲，王 海*，袁 珮，范 燕，邢化朝，高思田

1. 中国石油大学(北京)化工学院，北京 102249

2. 中国计量科学研究院，北京 100029

基于GIXRR反射率曲线的二氧化硅纳米薄膜厚度计算

马一博1,2，王梅玲2，王 海2*，袁 珮1，范 燕1,2，邢化朝1,2，高思田2

1. 中国石油大学(北京)化工学院，北京 102249

2. 中国计量科学研究院，北京 100029

为了快速、准确得到纳米薄膜厚度，采用Kiessig厚度干涉条纹计算薄膜厚度的线性拟合公式，计算了不同系列厚度(10～120 nm)的二氧化硅薄膜。薄膜样品采用热原子层沉积法(T-ALD)制备，薄膜厚度使用掠入射X射线反射(GIXRR)技术表征，基于GIXRR得到的反射率曲线系统讨论了线性拟合公式计算薄膜厚度的步骤及影响因素，同时使用XRR专业处理软件GlobalFit2.0比较了两种方法得到的膜厚，最后提出一种计算薄膜厚度的新方法-经验曲线法。结果表明：峰位级数对线性拟合厚度产生主要影响，峰位级数增加，厚度增大；峰位对应反射角同样对线性拟合厚度有较大影响，表现为干涉条纹周期增大，厚度减小。但峰位级数及其对应反射角在拟合薄膜厚度过程中引入的误差可进一步通过试差法，临界角与干涉条纹周期的校准来减小。对任意厚度的同一样品，线性拟合和软件拟合两种方法得到的薄膜厚度具有一致性，厚度偏差均小于0.1 nm，表明线性拟合方法的准确性。在厚度准确定值的基础上提出薄膜厚度与干涉条纹周期的经验关系曲线，通过该曲线，可直接使用干涉条纹周期计算薄膜厚度，此方法不仅省略了线性拟合过程中确定峰位级数及其对应反射角的繁琐步骤，而且避免了软件拟合过程中复杂模型的建立，对快速、准确获得薄膜厚度信息具有重要的意义。

厚度测量；掠入射X射线反射；二氧化硅薄膜；经验关系

引 言

在MOS/CMOS集成电路制造工艺中，二氧化硅纳米薄膜通常用作MOS晶体管的栅氧化层[1]，随着器件特征尺寸的不断减小，栅氧化层变得越来越薄。栅氧化层的厚度是决定集成电路抗漏电击穿能力的重要参数之一[2]，需要准确测量与控制。国际半导体技术路线图(ITRS)对栅氧化层厚度测量准确度提出明确要求：栅氧化层厚度测量结果的不确定度要达到4%以内[3]。因此，二氧化硅薄膜厚度的准确测量十分重要。

目前，常用纳米薄膜厚度测量方法主要包括掠入射X射线反射(GIXRR)、光谱椭偏(SE)、X射线荧光(XRF)、X射线光电子能谱(XPS)等。GIXRR是一种无损、快速检测手段，具有高测量重复性。但是，GIXRR测量数据尚需通过软件进一步拟合得到薄膜厚度，拟合过程所需的物理模型和参数确定非常复杂且耗时[4-5]。因此，众多研究者一直在寻求既可替代软件拟合又能快速准确得到薄膜厚度的新方法。

GIXRR利用薄膜对X光反射率的影响测量薄膜厚度。通常，X射线入射到基底表面时会发生镜面反射；但若基底表面被纳米薄膜覆盖，入射X光经过薄膜后也会在界面处发生反射，表面与界面的两束反射光发生干涉并形成周期振荡条纹，条纹周期反映出薄膜的厚度信息[6, 8]。一些研究者通过GIXRR反射率曲线得到快速计算薄膜厚度的线性拟合公式(1)—式(3)。

(1)

(2)

(3)

式中，mi表示第i级峰位(正整数)，θi是峰位i对应反射角[实验测量单位为角度，代入式(3)计算需转化为弧度]，λ是入射光波长(nm)，d为待测薄膜厚度(nm)。式(1)一般用来估算膜厚，所得膜厚无法满足薄膜精确测量要求。Gotszalk等[7]所使用的平方近似式(2)虽然能够满足厚度测量精度，但是所含参数入射光散射因子δ不能直接获得。崔建军等[8]基于GIXRR反射率曲线所得式(3)能够满足膜厚测量要求，且所含参数临界入射角θc可从反射率曲线的拐点处获得。然而，使用式(3)仍存在一些问题：SiO2/Si体系反射信号的快速衰减会造成振荡曲线不明显，其表现为低反射角范围内显示的峰位数少于实际的峰位数；反射率信号易受外界噪音干扰使振荡曲线不平滑，进而影响波峰位置的判断[9]。这些问题都是影响线性拟合公式计算薄膜厚度的重要因素，未有人细致研究过。本工作采用原子层沉积法(ALD)制得系列厚度的SiO2薄膜，通过GIXRR测量反射率曲线并结合式(3)计算薄膜厚度，系统讨论了峰位级数及其对应反射角、干涉条纹周期对线性计算薄膜厚度的影响；与此同时，提出一种快速、准确获取SiO2薄膜厚度的经验曲线新方法。

1 实验部分

1.1 样品处理

选用直径为6英寸单晶Si(100)片作为基底，依次经过异丙醇浸泡、淋洗、氮气吹干清洗步骤，立即转移至ALD反应腔。硅源采用二(异丙基)氨基硅烷、氧源采用臭氧。ALD制备时的基底温度300 ℃、沉积速率约0.12 nm·cycle-1，通过控制反应循环数制得7个不同厚度的样品。制备完成后待基底温度降至室温将其取出，切割成25 mm×20 mm的小片并保存在真空干燥器内待XRR表征。

1.2 XRR表征

XRR表征采用Rigaku Smart lab型X射线衍射仪。测量模式ω-2θ，功率40 kV×200 mA，入射狭缝0.05 mm，接收狭缝0.15 mm，扫描区间0°≤2θ≤5°，步长0.01°，扫描速率0.67°·min-1。样品表征前按照1.1中的清洗步骤进行处理，尽可能避免表面吸附影响测量厚度[12]。根据SiO2/Si薄膜结构[10-11]自下而上建立5层物理模型，即自然氧化层、过渡层1、SiO2主体、过渡层2和表面吸附层，使用软件Rigaku Global Fit 2.0拟合测量数据。

1.3 线性拟合公式计算膜厚

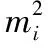
2 结果和讨论

2.1 XRR商业软件拟合厚度

RigakuGlobalFit2.0是一款商业化的XRR数据处理软件，可同时得到薄膜厚度、密度、粗糙度等信息。利用该软件拟合分析七个不同厚度样品的反射率曲线以得到SiO2薄膜厚度(dg)，厚度结果见表2；其中，样品1#(设计厚度10nm)的软件拟合结果如图1所示。

图1 样品1#的反射率测量结果及其拟合曲线Fig.1 The experimental reflectivity andits fitting curve of sample 1#

2.2 线性拟合影响因素

为了方便识别峰位及其对应的反射角，采用局部区域放大法处理反射率曲线。图2是样品6#(设计厚度100nm)局部区域反射率曲线放大图。图中平行y轴的虚线对应临界角位置2θc，带箭头线段依次对应待确定峰位的位置，圆圈所示为第1和2级峰位位置。

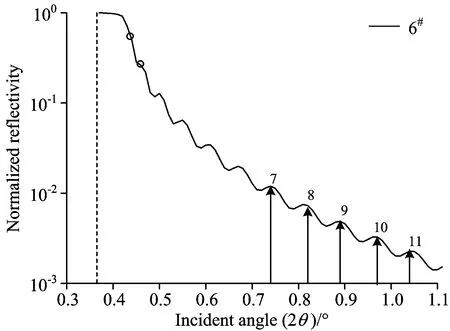
图2 样品6#的反射率测量曲线局部放大图Fig.2 Partial enlarged drawing of experimentalreflectivity curve of sample 6#

2.2.1 峰位级数对厚度的影响

式(3)中峰位级数直接影响厚度计算。图2所示第1和2级峰位位置不明显，容易造成峰位级数确认错误。因此，针对相同峰位位置设定不同级数并分别计算厚度，然后将其与软件拟合厚度相比较以确定正确的峰位级数。表1列出图2箭头标记峰位位置所设定的五组不同峰位级数，以及计算得到的对应厚度(dl)。结果表明：对于名义厚度100nm的二氧化硅薄膜，峰位级数每增加1级，计算的厚度平均增加5.693nm，其中根据峰位级数(7，8，9，10，11)计算得到的厚度(102.433nm)最接近软件拟合结果(103.400nm)。

2.2.2 峰位对应反射角对厚度的影响

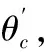
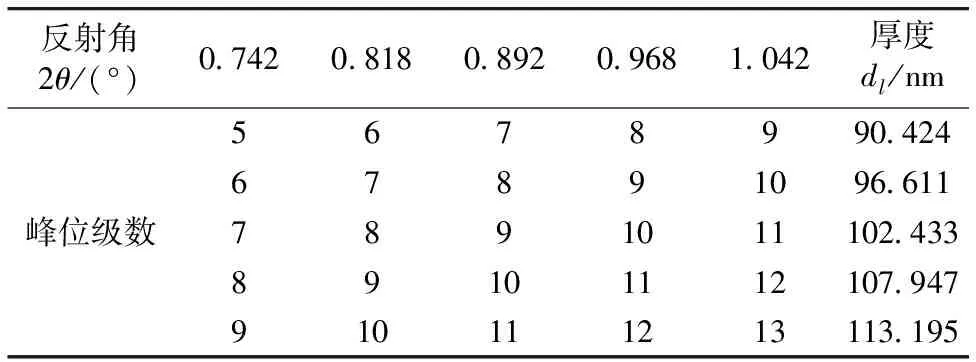
表1 五组峰位级数及其对应的计算厚度

2.2.3 干涉条纹周期对厚度的影响

为了消除相邻峰位对应反射角的读数误差以及简化反射角的确定过程，引入参数干涉条纹周期Δθ(定义：相邻峰位对应的反射角之差，实验测量单位为角度，代入式(4)计算需转化为弧度)。读取其中一级峰位mi对应的反射角θi，相邻峰位级数mi+1对应的反射角可用θi+Δθ计算得到，其他峰位对应的反射角依次类推。此时式(3)变为式(4)。

(4)

通过上述三个因素对计算膜厚影响的分析，可知：为了保证线性拟合公式计算薄膜厚度的准确性和可靠性，需要正确确定峰位级数、通过临界角校准峰位对应的反射角以及选择适当的干涉周期。

2.3 干涉条纹周期与薄膜厚度的经验曲线

在考虑峰位级数、峰位对应反射角和干涉条纹周期对厚度计算影响的基础上，通过式(3)计算7个系列样品的SiO2薄层厚度(dl)，并将其与软件拟合结果(dg)作比较，结果见表2。可以看出：线性拟合薄膜厚度与其对应的干涉条纹周期呈指数衰减关系；dl相对dg的偏差均基本小于0.1 nm，且两个厚度存在线性关系dl=0.004+1.001dg，厚度一致性说明线性拟合公式计算得到的厚度是准确可靠的。

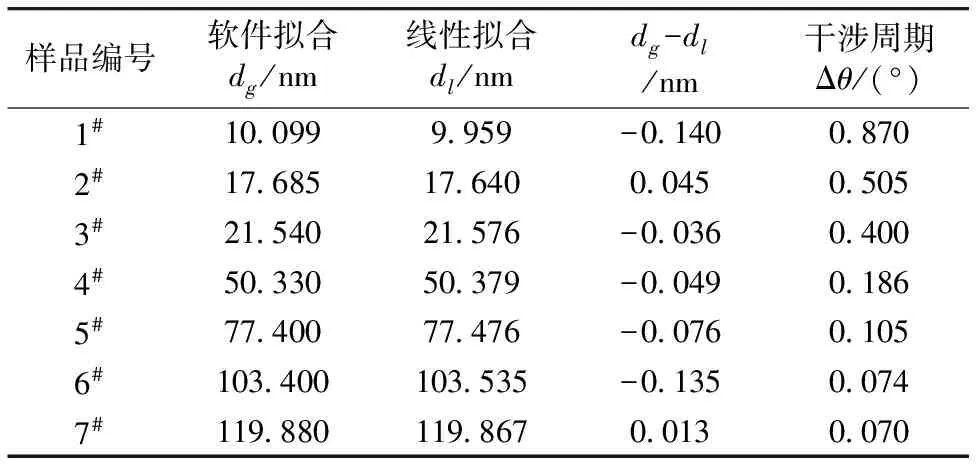
表2 线性计算厚度与软件拟合厚度对比

此外，线性拟合厚度dl及其对应干涉条纹周期Δθ存在一一对应关系，这样就可得到一种计算Si上SiO2薄膜厚度的新方法——经验曲线法(见图3)。在相同的实验条件下，测量未知厚度SiO2薄膜反射率曲线并读取干涉条纹周期Δθ，通过插入法就能够得到薄膜厚度，或者直接代入经验曲线对应式(5)，式中Δθ计算时采用角度值，对读取角度直接计算厚度更方便。

(5)

式中，Δθ单位度，d单位nm。相对其他方法而言，经验曲线方法具有快速、准确和简单易行的特点。

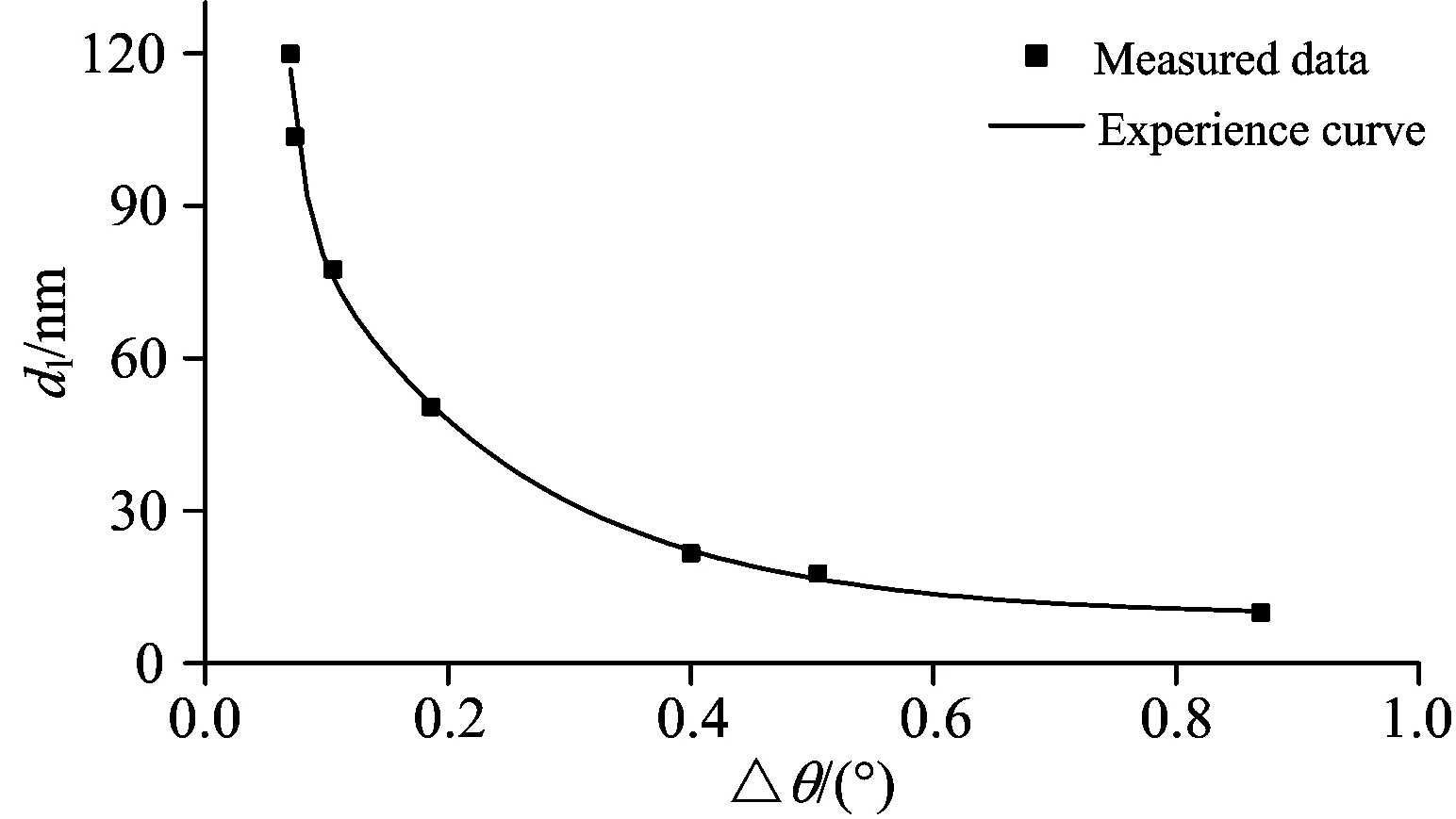
图3 薄膜厚度dl与干涉条纹周期Δθ之间的经验曲线

Fig.3 The empirical curve between the film thickness (dl) and the interference fringe period (Δθ)

3 结 论

采用原子层沉积法(ALD)制得系列厚度的SiO2薄膜，基于GIXRR反射率曲线及线性拟合公式计算SiO2薄膜厚度。峰位级数及其对应的反射角直接、显著地影响薄膜厚度的计算，干涉条纹周期同样对薄膜厚度计算产生间接影响；这些影响可通过本法消除或校准。推导得到的薄膜厚度与干涉条纹周期经验曲线能够快速、准确地获得SiO2薄膜的厚度，在实际应用中具有重要价值。

[1] Lee W J, Chun M H, Cheong K S. Solid State Phenomena, 2007, 124-126: 247.

[2] van der Marel C, Veerheijen M A, Tamminga Y. Journal of Vacuum Science and Technology A: Vacuum, Surfaces and Films, 2004, 22: 1572.

[3] WANG Hai, LIU Fen, KAN Ying, et al(王 海，刘 芬，阚 莹，等). Acta Metrologica Sinica(计量学报), 2013, 34(6): 617.

[4] Terada S, Murakami H, Nishihagi K. Thickness and Density Measurement for New Materials with Combined X-Ray Technique. Advanced Semiconductor Manufacturing Conference, 2001 IEEE/SEMI, IEEE, 2001. 125.

[5] Parrat L G. Physical View, 1954, 95(2): 359.

[6] CHEN Guo-feng, YANG Chuan-zhen, HUANG Yue-hong(程国峰，杨传铮，黄月鸿). X-Ray Analysis of Nano Materials(纳米材料的X射线分析). Beijing：Chemical Industry Press(北京：化学工业出版社), 2010. 171.

[7] Serafinczuk J, Pietrucha J, Schroeder G, et al. Optica Applicata, 2011, 41(2): 315.

[8] CUI Jian-jun, GAO Si-tian(崔建军，高思田). Acta Physica Sinica(物理学报), 2014, 63(6): 2.

[9] Gibaud A, Hazra S. Current Science, 2000, 78(12): 1467.

[10] Windover D, Armostrong N, Cline J P, et al. AIP Conference Proceedings, 2005, 788: 161.

[11] Luh D A, Miller T. Physical Review Letters, 1997, 79(16): 3014.

[12] Gil D L, Windover D. Journal of Physics D: Applied Physics, 2012, 45(23): 1.

*Corresponding author

(Received Jul. 24, 2015; accepted Nov. 14, 2015)

Thickness Calculation of Silicon Dioxide Nano-Film Based on GIXRR Reflectivity Curve

MA Yi-bo1,2, WANG Mei-ling2, WANG Hai2*, YUAN Pei1, FAN Yan1,2, XING Hua-chao1,2, GAO Si-tian2

1. College of Chemical Engineering, China University of Petroleum (Beijing), Beijing 102249, China

2. National Institute of Metrology，China, Beijing 100029, China

To obtain nanometer thin film thickness fastly and accurately, a formula of linear fitting method based on the periodic Kiessig fringes for thickness determination is applied, and a series of SiO2nanometer films on Si substrate with the film thickness ranging from 10 to 120 nm have been calculated with the formula. These samples are prepared with thermal atomic layer deposition (T-ALD) process and film thickness is measured with grazing incidence X-ray reflection (GIXRR) technique, in addition, the linear fitting procedure and several influencing factors among it are studied, all of the work is based on the reflectivity curve from GIXRR experiment. While at the same time, another fitting method based on a soft named Global Fit2.0 is brought into this study to compare the two obtained thicknesses from two kinds of analysis methods. In the end a novel method for film thickness determination-empirical curve is presented. The results show that: during the linear fitting process, the peak position series have a main effect on thickness determination, thickness will increase when the peak position adds up; Besides, any peak’s corresponding reflection angle also has a significant effect on the thickness determination, it is expressed in the form of interference fringe period, thickness will decrease while the interference fringe period increases, however, the errors from either peak series or fringe period can be further weakened with trial and error method, calibration procedure of critical angle and interference fringe period individually. Choosing the same sample with random thickness, no matter using the linear fitting and soft fitting method, the two gained film thicknesses are consistent and the thickness deviation is less than 0.1 nm, which illustrates the accuracy of linear fitting method for thickness determination. An empirical relationship between film thickness and interference fringe period is then put forward on the foundation of the accurate thickness determination, according this curve, the target film thickness is directly got by putting an interference fringe period in the empirical curve. This novel method not only avoids the messy procedure of choosing peak position series or their corresponding angles during linear fitting process, but also avoids the complex task of building a correct structure for soft fitting process; it is of great significance in confirming thin film thickness with quick speed and high accuracy.

Thickness measurement; Grazing Incidence X-ray Reflection; Silicon dioxide thin film; Empirical relationship

2015-07-24，

2015-11-14

国家科技支撑计划项目(2011BAK15B05)资助

马一博，1991年生，中国石油大学(北京)化工学院硕士研究生 e-mail：1750593719@qq.com *通讯联系人 e-mail：wanghai@nim.ac.cn

O434.1

A

10.3964/j.issn.1000-0593(2016)10-3265-04