DLA光源质量对光栅-外腔谱合成系统光束质量的影响

杨 磊，钟哲强，吴 真，张 彬

四川大学电子信息学院，四川 成都 610065

DLA光源质量对光栅-外腔谱合成系统光束质量的影响

杨 磊，钟哲强，吴 真，张 彬*

四川大学电子信息学院，四川 成都 610065

在二极管激光阵列(DLA)光栅-外腔谱合成系统中，由于DLA存在子单元光束发散角、“smile”效应的位置偏差及指向性偏差等因素的综合作用，将导致合成光束的光束质量降低。综合考虑DLA子单元光束发散角、“smile”效应等因素对谱合成系统中光束传输特性的影响，建立了DLA光栅-外腔谱合成系统的光传输模型，进而对谱合成系统中DLA子单元光束发散角、“smile”效应的位置偏差及指向性偏差等因素对合成光束的光束质量影响进行了定量分析。结果表明，DLA光源质量会明显影响合成光束的光束质量：DLA子单元光束发散角和“smile”效应引入的指向性偏差越大，合成光束的光束质量就越差；“smile”效应引入的位置偏差在合束方向上对合成光束的光束质量没有影响，而在非合束方向上引入的位置偏差将会明显降低合成光束的光束质量。在实际工作应用中，需要采取措施提高DLA光源质量，以减小对合成光束的光束质量影响。

二极管激光阵列；光栅-外腔谱合成；光束质量；光束发散角；“smile”效应

引 言

激光二极管阵列(diode laser array，DLA)具有很高的电光转换效率，且因其寿命长、体积小、重量轻、价格便宜等优点，已广泛应用于光谱分析、军事、航天、通信等领域[1-3]。在高功率激光系统中，通过对不同排列方式的激光二极管阵列进行光束合成，在提升输出功率的同时，还能得到很好的输出光束质量。因此，作为光束合成典型方式之一的DLA光栅-外腔谱合成系统受到人们的关注。然而，由于DLA子单元自身发散角的存在，以及封装引入的“smile”效应等因素，致使合成光束的光斑变大，并产生明显旁瓣，进而导致合成光束的光束质量难以达到预期的效果[4-5]。近年来，为获得更高功率、更好光束质量的合成光束，国内外针对DLA快慢轴整形与“smile”效应测量与封装等问题提出了很多新方法[4-9]。然而，尚缺乏光束自身发散角与“smile”效应等因素对DLA光栅-外腔谱合成系统合成光束的光束质量影响规律进行定量分析。

本文在对DLA光栅-外腔谱合成系统中激光束传输特性进行分析的基础上，进一步考虑光源自身发散角、“smile”效应等因素对激光束传输特性的影响，建立了DLA光栅-外腔谱合成系统的光传输模型，进而数值模拟和分析了光源自身发散角、“smile”效应等因素对合成光束的光束质量影响。

1 理论模型

1.1 DLA光栅-外腔谱合成系统

图1给出了DLA光栅-外腔谱合成系统结构示意图。在图1中，谱合成系统由DLA、变换透镜、闪耀光栅以及输出耦合镜构成。变换透镜的作用是将不同单元的子光束以不同的入射角入射到闪耀光栅上。闪耀光栅的作用是通过光栅方程将不同波长、不同入射角的子光束以相同的衍射角出射到输出耦合镜上。因此，DLA的每一子单元均可看作与外腔构成一个完整的子谐振腔，整个光谱合成系统可看成是多个独立的、振荡在不同波长的子谐振腔在光谱合成方向的集合，且因各子谐振腔具有相同的输出镜而使DLA各单元在近场和远场保持重叠。

1.2 光源模型

1.2.1 光源自身发散角

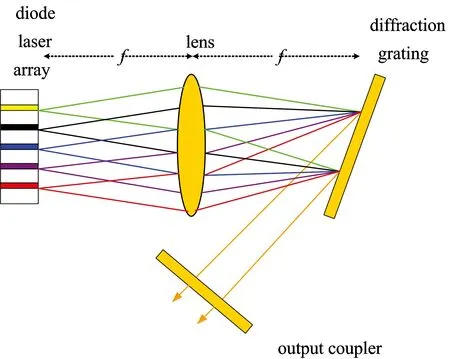
图1 DLA光栅-外腔谱合成系统示意图

经光束整形后，DLA在快轴方向的光束近似为基模高斯光束，而在慢轴方向的光束近似为超高斯光束[10]。在常见的谱合成系统中，由于快轴方向为光束的合束方向，因而本文重点对该方向进行讨论。此外，实际应用中DLA子单元的输出光束往往具有一定的发散角，可引入一个球面位相Rx进行表征，则DLA子单元的输出光场可表示为

(1)

式(1)中，k=2π/λ，λ为每个子单元对应的波长；E0为光场初始振幅；wx为x(快轴)方向的束腰宽度。

1.2.2 “smile”效应

对于DLA来说，由于半导体激光器在外延生长及封装时应力的引入，使得封装后的半导体激光器芯片出现弯曲，bar条上的每个发光点在快轴方向就会出现一定的弯曲起伏，存在位置偏差和指向性偏差，出现所谓的“smile”效应。对于谱合成系统来说，“smile”效应会使得各个合束单元经由外腔的反馈强度不同，从而造成个别合束单元的快慢轴光束质量退化[11]。

“smile”效应的影响主要体现在DLA中各子单元相对位置偏差和指向性偏差的影响[14]，相应的DLA子单元输出光场可表示为

(2)

式(2)中，X为发光单元在“smile”效应位置偏差下快轴方向上的相对位置偏差量；θx为每个单元由指向性偏差引起的角度偏差量。

在综合考虑光束自身发散角与“smile”效应的DLA光源模型为式(3)

(3)

2 DLA谱合成系统的光传输模型

针对DLA子单元自身发散角、“smile”效应等因素对系统中光传输特性的影响展开分析，进而建立DLA光栅—外腔谱合成系统的光传输模型。在分析“smile”效应在合束方向上引入的位置偏差时，需要考虑腔长的变化导致光束中心波长的变化；在分析DLA子单元自身发散角和“smile”效应引入的指向性误差时，需要考虑对子光束在光栅上的入射角、衍射角以及光栅面上光程差的影响。

以透镜的前焦平面为x″轴、透镜的光轴为z″轴建立坐标系，入射光波场模型如图2所示。

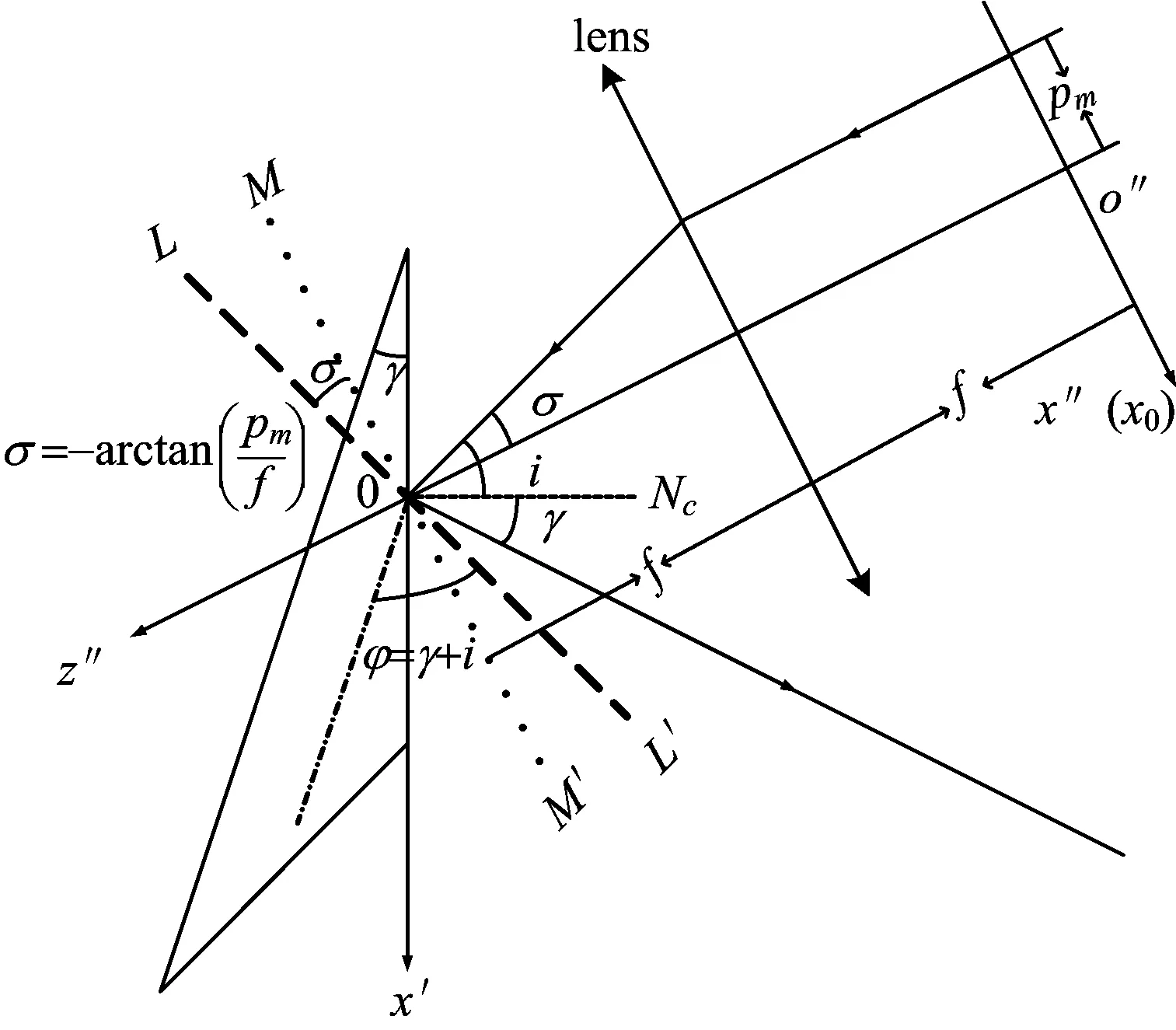
图2 子光束在闪耀光栅入射面传输的示意图

图2中，MM′表示透镜的后焦面，LL′表示经透镜变换后光束的中心光线在光栅中心的垂线[14]，假定DLA中相邻两个子光源的间距为Δp，每一子光束的束腰宽度为w0，则编号为m的子光束的在z″=0处的光场为

(4)

式(4)中，km=2π/λm，λm为第m子光束对应的波长；pm=mΔp为编号m的子光源中心坐标。在考虑到光束自身发散角，“smile”效应的指向性偏差和位置偏差的影响时，Xm为位置偏差量，且Xm=random(-1, 1)×Xmax，Xmax为位置最大偏差量；Rxm为子光束的波前曲率半径，经过透镜传输后，每一子光束的波前曲率半径对应有一个发散角δxm；θxm为编号为m的子光束的指向性偏差角，不妨设发光单元的最大指向性偏差角为θ，则对于每个单元来说指向性偏差角为θxm=random(-1, 1)×θ。

将式(4)代入柯林斯公式[12]，可得到DLA发出的子光束从光源传输到闪耀光栅入射面后，在光栅面(x″,z″)处的光场为式(5)

(5)

将闪耀光栅中心槽面的中心点置于透镜的焦点上，则从光源到闪耀光栅入射面之间的光学系统的ABCD矩阵为

(6)

式(6)中，A=(2f-z″)/f，B=f，C=-1/f，D=0。

图2中，在透镜后焦面上z″和x″之间的关系为式(7)

(7)

在综合考虑光束自身发散角，“smile”效应的指向性偏差和位置偏差的影响时，经分析可知，光源的位置偏差仅仅会改变与中心位置的间距变化，第m个子光源与中心位置的距离为pm′=pm+Xm。

基于每个槽面上光波复振幅相同的假设，可得到槽序号n与x″之间的关系为

(8)

式(8)中，d为闪耀光栅的周期；γ为光栅刻槽倾角；αm为第m条子光束在光栅面上的入射角。

将式(6)—式(8)代入式(5)，即可得到在光栅面上的光场分布Em(x″,z″)。

由于位置偏差会致使发光子单元的中心波长发生改变[12-13]，DLA各个子单元在只考虑“smile”效应的位置偏差时，由于中心波长同步变化，其在光栅的入射角和出射角并不会改变。第m个子单元波长可表示为[14]

(9)

式(9)中等号右边第一项λ0表示DLA中心单元的中心波长，第二项表示进一步考虑了位置偏差影响的第m个单元与中心单元的波长差。式(9)中，α0为中心光束的入射角，根据光栅的主闪耀条件，以-1级衍射为例，则α0=arcsin[-λ0/(2d)]；λ0为中心光束的波长。

自身发散角和指向性偏差不会影响波长的变化，但会使光栅的入射角和出射角发生改变。在光源受到自身发散角的影响时，图3给出了谱合成系统在自身发散角影响下光栅面的示意图。

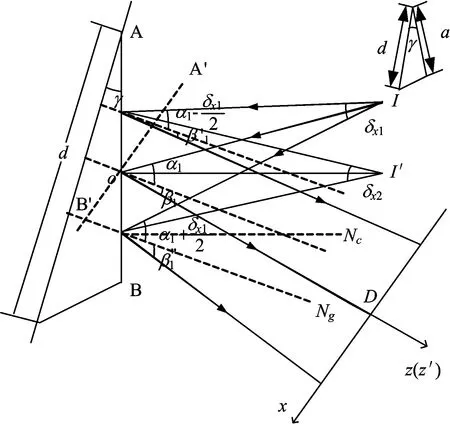
图3 在自身发散角影响下光束在光栅面的示意图

在图3中，光栅周期为d，刻槽倾角为γ，刻槽宽度为a，Ng为光栅法线，Nc为光栅槽面法线，第m条光束的入射角和衍射角分别为βm和βm。其中，以衍射角β方向为出射光束的传输方向z′轴，接收屏x垂直于光束传输方向z′轴，假设每一个槽面都存在一个等效的虚拟槽面，该方向沿x′轴，A′B′为虚拟槽面，AB为实际槽面[17]。对于光源自身来说，每一束光的一个曲率半径Rxm值对应一个发散角δxm。在经变换透镜后，将编号为m子光源发出的子光束分为L(L→∞)条子光线。因此，每条子光线对应在光栅面上的入射角不同，可以得到中心的光线入射角为αm，则第h条光线对应入射角为α=αm-δxm/2+(h-1)δxm/(L-1)。

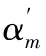
于是，当同时考虑发散角与指向性偏差时，经过变换透镜后，第h条光线对应的入射角为

(10)

式(10)中，等号右边第一项表示理想条件下中心光线的入射角，第二、三项表示光源发散角对第h条光线入射角的影响，第四项表示指向性偏差对第h条光线入射角的影响。

根据光栅方程，光栅衍射角会随着入射角的改变而变化，假设在无自身发散角影响时，-1级衍射角为βm，βm可根据光栅方程求得：βm=arcsin[sin(αm)+λm/d]。而有发散角影响时，每条光线对应的衍射角为β，为满足不同角度、不同波长的入射光在接收屏上相同位置接收到最大峰值。因此，根据光栅方程可得到其衍射角β为式(11)

(11)

从图3中可以看出，由于受到DLA子单元发散角的影响，每条光线对应在第n个虚拟槽面与x轴之间的距离zn为式(12)

(12)

光束自身发散角和指向性偏差的存在，会引起在光栅上传输时槽内光程差和槽间光程差的改变。在图4中，I′与I是相邻子单元入射至光栅面的光线，不妨设I′的指向性偏差角为θx1，发散角为δx1。I的指向性偏差角为θx2，发散角为δx2，则两条光线由指向性偏差引起的相对偏差角为θx=θx1-θx2。而I′和I由自身发散角引起的相对偏差角为δx=δx1-δx2。于是，两条光线的相对偏差角为ηx=θx+δx。

根据图4可知，第m个子光源的第h条光线入射到第n个虚拟槽面上的光程差为

(13)

式(13)中，Δ0=ndsinα，Δx=ndcosβ，CΔ=[sin(α-γ)-sin(γ+β)]/cos(γ+β)，Δηx=zn/cosηx-zn。

考虑到光栅的有效衍射面，则有式(14)

(14)

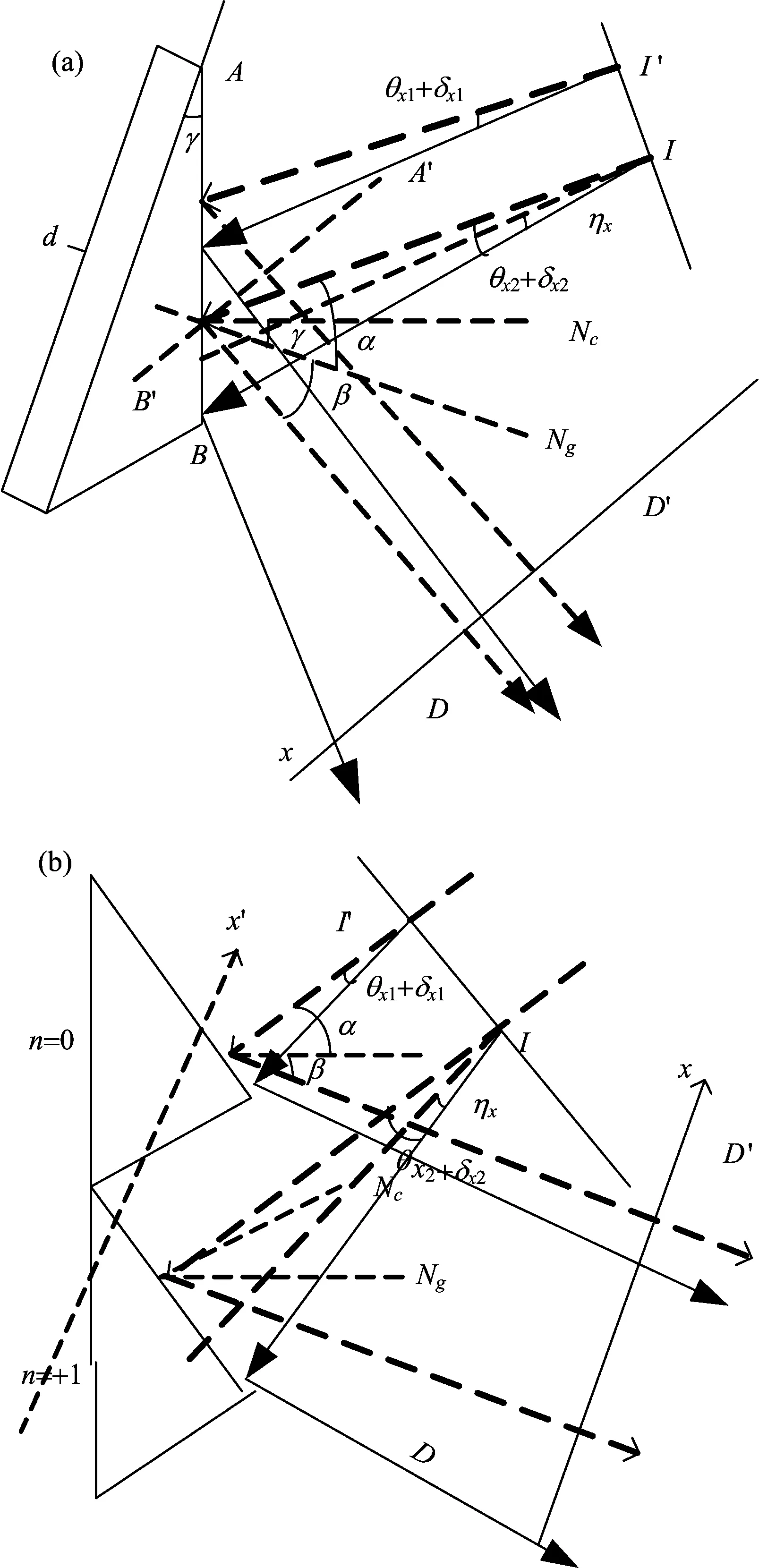
图4 存在指向性偏差和发散角时，光栅面上光程差示意图

Fig.4 Schematic illustration of optical path difference when existing divergence angle and direction angle deviation

(a)：Optical path difference in groove；(b)：Optical path difference in adjacent groove

于是，第n个光栅槽面在接收屏处的衍射光场就等效于第n个虚拟槽面经距离zn的衍射，接收屏上的光场即为所有虚拟槽面经不同距离zn衍射的光场的叠加。利用式(4)—式(14)，综合考虑子单元发散角、“smile”效应等因素影响下，可得到第m个子光源的第h条光线经透镜和光栅衍射后在接收屏上的光场表达式为式(15)

(15)

第m个子光源的光强分布可以表示为式(16)

(16)

因此，DLA谱合成系统(含2M+1个子单元)合成光束的光强分布可以表示为式(17)

(17)

3 数值模拟

以5束子光源为例，假设阵列光源中相邻子光源的中心间距Δp=500 μm，子单元输出光束束宽w0=100 μm，透镜焦距f=30 cm，光栅线密度l=600 mm-1，光栅刻槽倾角γ=15.8°，中心发光单元的中心波长为800 nm。图5(a)分别给出了在理想情况下，输出耦合镜面上合成光束的光强分布(M2=1.00)，以及在综合考虑各项因素(最大子光束发散角为17.5 mrad，最大指向性偏差角为2 mrad，最大位置偏差为25 μm)时，合成光束的光强分布(M2=3.61)，图5(b)则给出了理想情况和非理想情况下，合成光束的光束直径平方与传输距离的关系。

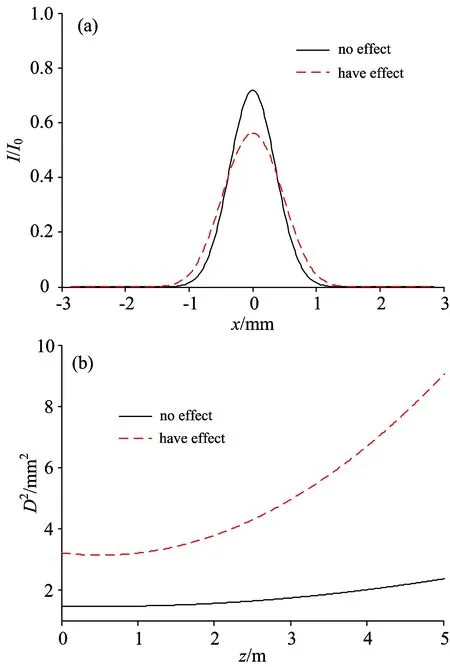
图5 合成光束及其远场光束直径平方的变化规律

(a)：Intensity distributions；(b)：Variation of beam diameter square with propagation distance

从图5(a)中可以看出，在理想情况下，合成光束的光束质量最好。而在受到自身发散角、“smile”效应的影响时，光斑变大，峰值光强减小，光束质量变差。从图5(b)可以看出，在DLA光源质量不理想时，合成光束的光斑尺寸有所增大，其发散角也明显增大。分别对DLA子单元发散角、“smile”效应等因素对合成光束光强及光束质量的影响进行数值模拟和分析。为简便起见，仅给出合成光束在输出耦合镜上的光强分布及其光束质量的变化。

3.1 子单元自身发散角对合成光束的光束质量影响

通常，DLA子光束经过准直透镜准直后，其快轴方向的发散角一般不到1°(即17.5 mrad)[16]。为简便起见，讨论自身发散角影响时，每一单元子光束的发散角大小是相同的，故发散角在光栅面上引起的偏差角δx=0。图6(a)给出了只考虑子单元自身发散角时，DLA子单元经过准直透镜后，在无发散角和最大发散角分别为7.0 mrad、14.0和35.0 mrad时的合成光强分布，图6(b)给出了DLA子单元经过准直透镜后，最大发散角在0～17.5 mrad之间时，合成光束的光束质量随发散角的变化。

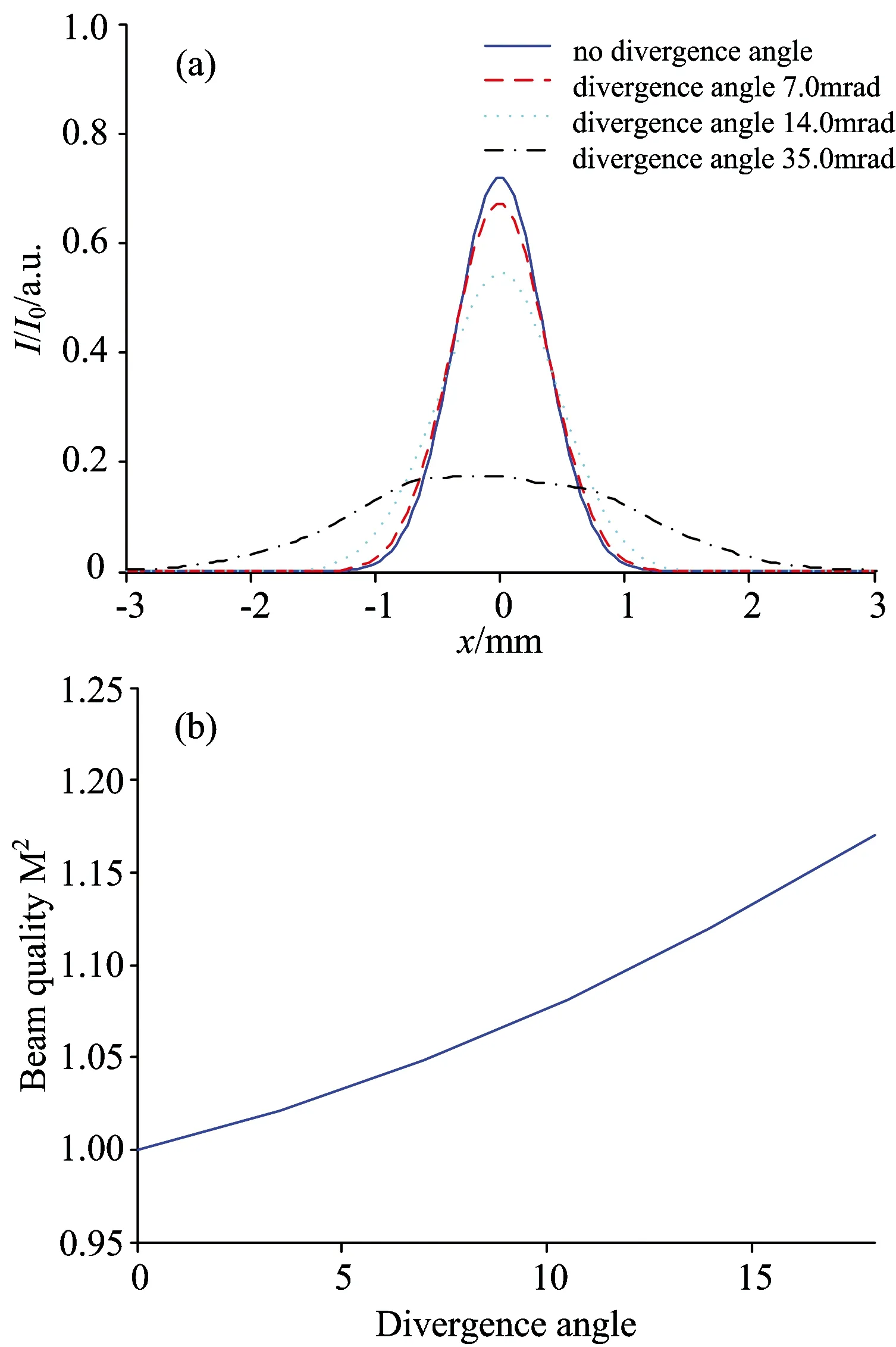
图6 不同发散角时，合成光束的光束质量和光强分布

从图6中可以看出，在无子单元发散角影响时，合成光束的光束质量最好。然而，随着子单元发散角的增大，合成光束的光斑尺寸增大，光强峰值减小，光束质量也随之降低。当发散角增大到一定程度时，合成光束的光斑尺寸显著增大，从而致使合成光束的光束质量严重降低。

3.2 “smile”效应对合成光束的光束质量影响

3.2.1 指向性误差对合成光束的光束质量影响

当只考虑“smile”效应的指向性偏差时，在最大偏移角θ不同时，图7(a)给出了无指向性偏差和最大指向性偏差角分别为0.70，1.40和2.45mrad时的合成光束光强分布，图7(b)则进一步给出了合成光束的光束质量随最大指向性偏差角的变化规律。

图7 不同最大偏移角时，合成光束的光强分布和光束质量

Fig.7 Intensity distributions and beam quality of the combined-beam for different angle of maximum excursions

(a)：Intensity distribution；(b)：Beam quality

由图7(a)中可以看出，无指向性偏差时，合成光束的光束质量较高。然而，随着最大指向性偏差角的增大，合成光束的峰值光强有所降低，光斑尺寸逐渐增大，合成光束的光束质量也明显下降[如图7(b)所示]。当最大指向性偏差角增大到一定程度时，各子单元的光束不再汇聚至中心位置，从而导致合成光束中心变得平坦，并产生旁瓣，光束质量明显降低。

3.2.2 位置偏差对合成光束的光束质量影响

当只考虑“smile”效应的位置偏差时，分别对在无位置偏差和最大偏移量为25和50 μm时的合成光束光强进行模拟，其结果如图8所示。

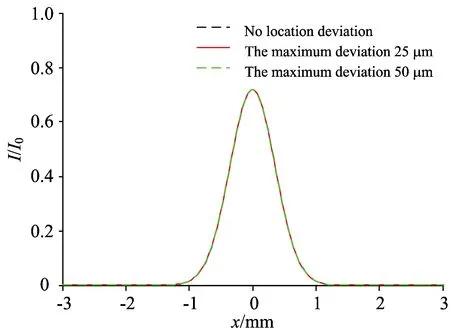
图8 不同最大偏差时合成光束的光强分布

从图8可以看出，当只考虑快轴x方向的位置偏差时，合成光束的光束质量不会发生变化。这是因为子单元位置偏移的存在，将导致光束的中心波长发生改变，因而并不改变子单元光束在光栅面的入射角和衍射角，也不会影响合成光束的光束质量。值得指出的是，在非合束方向上位置偏差将造成合成光束光斑变大，从而降低合成光束的光束质量。

4 结 论

在DLA光栅-外腔谱合成系统中，由于DLA子单元自身发散角的存在，以及“smile”效应的影响，会导致DLA谱合成系统中合成光束的光束质量下降。基于DLA光栅-外腔谱合成系统中光束传输特性分析，建立了在综合考虑DLA子单元发散角、“smile”效应等因素影响时的谱合成系统光传输模型。在此基础上，开展了DLA子单元发散角和“smile”效应对合成光束的光束质量影响研究。结果表明：在DLA光栅-外腔谱合成系统中，合成光束的光束质量随着DLA子单元自身发散角和“smile”效应引入的指向性偏差角的增大而明显变差；在合束方向上，“smile”效应引入的位置偏差并不会对合成光束的光束质量造成明显影响。由此可见，在实际工作中，需要对DLA质量进行优化，包括利用准直透镜或准直微透镜组对激光器阵列单元发出的子光源进行整形以减小子光束发散角，以及对DLA封装方式进行优化等，从而有效提高合成光束的光束质量。

[1] Chann B，Huang R K，Missaggia L J. Opt. Lett., 2005, 30(16): 2104.

[2] ZHAO Jie, HAN Ye-xing, GUO Jie, et al(邵 杰，韩叶星，郭 杰，等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2014, 34(7): 1774.

[3] Zhu H，Ruset I C，Hersman F W. Opt. Lett., 2005, 30(11): 1342.

[4] LI Ge, ZHENG Gang, LEI Jun, et al(李 弋，郑 钢，雷 军，等). High Power Laser and Particle Beams(强激光与粒子束), 2014, 26(3): 26031004.

[5] Yang Z, Wang H, Li Y, et al. Optics Communications, 2011, 284(21): 5189.

[6] Ganesh S, Gupta R. Journal of Refractive Surgery, 2014, 30(9): 590.

[7] MENG Hui-cheng, TAN Hao, LI Jian-min, et al(孟慧成，谭 昊，李建民，等). Laser & Optoelectronics Progress(激光与光电子学进展), 2015, 52: 02003.

[8] Talbot C L, Friese M E J, Wang D, et al. Applied Optics, 2005, 44(29): 6264.

[9] PAN Fei, YAO Shun, JIA Guan-nan, et al(潘 飞，尧 舜，贾冠男，等). Semiconductor Optoelectronics(半导体光电), 2014, 1: 9.

[10] Friedrich Bachmann, Peter Loosen, Reinhard Poprawe. High Power Diode Lasers Technology and Application. Berlin: Spring, 2006. 138.

[11] MENG Hui-cheng, WU De-yong, TAN Hao, et al(孟慧成，武德勇，谭 昊，等). Chinese Journal of Lasers(中国激光), 2015，42(3): 0302003.

[12] ZHANG Yan, ZHANG Bin, ZHU Song-jun(张 艳，张 彬，祝颂军). Chinese Journal of Physics(物理学报), 2007, 56(8): 4590.

[13] PAN Lei-lei, ZHANG Bin, YIN Su-qin, et al(潘雷雷，张 彬，阴素芹，等). Chinese Journal of Physics(物理学报), 2009, 58(12): 8289.

[14] FEI Bing, WANG You-zi, LIU Tao, et al(费 冰，王悠子，刘 涛，等). Laser & Optoelectronics Progress(激光与光电子学进展), 2012, 49(7): 108.

(Received Jul. 29, 2015; accepted Nov. 18, 2015)

*Corresponding author

Effects of the DLA Light Source Quality on the Beam Quality of Combined Beam in Spectral Beam Combining Systems with Grating-External Cavity

YANG Lei，ZHONG Zhe-qiang，WU Zhen，ZHANG Bin*

School of Electronics and Information Engineering, Sichuan University, Chengdu 610065，China

In Diode Laser Array (DLA) spectral beam combining (SBC) systems with grating-external cavity, the beam quality of the combined beam tends to degrade due to comprehensive function of factors involving divergence angle of light, positional deviation and direction angle deviation caused by “smile”effect of emitters, etc.. Based on the consideration of the effects of the divergence angle and “smile”effect of DLA emitters on the beam propagation characteristics, the light propagation model of DLA SBC systems with grating-external cavity has been built up, and the effects of divergence angle and the positional deviation and direction angle deviation caused by “smile”effect of DLA emitters on the beam quality of the combined beam in SBC systems have been analyzed quantitatively. The results indicate that, the beam quality of the combined beam would be significantly affected by the DLA light source quality, i.e., the bigger the divergence angle and the direction angle deviation caused by “smile”effect are, the worse the beam quality of the combined beam is. The positional deviation of emitters in beam-combination direction caused by “smile”effect has little impact on the beam quality of the combined beam, whereas the positional deviation in non beam-combination direction would significantly degrade the beam quality of the combined beam. In practical applications, measures should be taken to improve the DLA light source quality in order to eliminate the effect on the beam quality of the combined beam.

Diode laser array；Spectral beam combing with grating-external cavity; Beam quality; Divergence angle; “smile”effect

2015-07-29，

2015-11-18

中国工程物理研究院高能激光科学与技术实验室基金项目(2014HEL03)，科技部创新人才推进计划重点领域创新团队(2014RA4051)资助

杨 磊, 1990年生，四川大学电子信息学院硕士研究生 e-mail: 534970335@qq.com *通讯联系人 e-mail: zhangbinff@sohu.com

O436

A

10.3964/j.issn.1000-0593(2016)10-3381-07