一种改进的遥感影像地形校正方法
臧 熹,杨 博,齐建伟,向夏芸
(1. 武汉大学,湖北 武汉 430072; 2. 中国国土资源航空物探遥感中心,北京 100083)
An Improved Topographic Correction Method of Remote-sensing Images
ZANG Xi,YANG Bo,QI Jianwei,XIANG Xiayun
一种改进的遥感影像地形校正方法
臧熹1,杨博1,齐建伟2,向夏芸1
(1. 武汉大学,湖北 武汉 430072; 2. 中国国土资源航空物探遥感中心,北京 100083)
An Improved Topographic Correction Method of Remote-sensing Images
ZANG Xi,YANG Bo,QI Jianwei,XIANG Xiayun
摘要:地形校正是遥感影像定量化应用环节之一,以往的地形校正研究多是针对一景影像中很小的局部影像块来进行处理研究的,对整景大场景影像进行地形校正的研究尚不多。基于此,本文利用高分一号的宽视场相机拍摄的16 m分辨率的遥感影像,研究了大场景下地形校正方法,对C校正模型进行了改进,在C校正模型中加入了反射角的影响,并且验证了改进模型的合理性;最后对改进的模型与余弦校正模型、传统的C校正模型的处理结果进行了比较。通过分析,利用改进的模型,影像的标准差普遍变小,影像校正后的阴阳坡亮度值趋于一致的趋势更明显。试验结果表明,对大场景、非星下点成像的遥感影像利用改进模型进行地形校正效果明显增强。
关键词:地形校正;宽幅;C校正模型;反射角
一、引言
卫星传感器获得的影像由于受到地形起伏即坡度和坡向变异的影响而导致阴阳坡影像亮度值的差异,尤其在丘陵地带和山区,地形坡度、坡向和太阳光照几何条件等对遥感影像的亮度值的影响是非常显著的,朝向太阳的坡面会接收到更多的光照,在遥感影像上色彩自然要亮一些,背向太阳的阴面由于反射的是天空散射光和邻近地物的散射光,在图像上表现得要暗淡一些,会出现同物异谱或同谱异物的现象。复杂地形地区遥感影像的这种辐射畸变称为地形效应,这种现象严重干扰了影像中地物的光谱信息,从而导致这些地区数字遥感影像自动分类的错分、难分现象,严重影响着数字遥感影像的信息提取精度和使用[1]。因此必须对地形效应进行校正处理,即地形校正。目前的地形校正主要是基于太阳入射角的地形校正模型,其主要目的是消除影像亮度值与太阳入射角的关系,将影像斜面上的亮度值投影到水平面上来,从而达到地形校正的目的。
现有的地形校正模型很多,其中C校正模型因其简单的使用条件和输入参数及较好的普适性,成为应用最广泛的校正模型之一。之前的研究对象大都是选取一景影像的一小部分影像块,此时,影像覆盖范围比较小,像元数量比较少,像元的反射角对C校正模型经验系数的拟合可能没有太大的影响,而且可以不用考虑像元的反射角在影像块内部的差异。但是当遥感影像的幅宽比较宽时,由于覆盖区域广,一景影像的像元数量非常多,在成像范围内,像元的反射角及像元在景内位置的差异引起的反射角的变化对整景影像的校正方程的相关性及拟合经验系数的计算就可能产生累积性和趋势性的影响。尤其是当卫星不是星下点成像时,反射角的影响可能会更明显。对于大场景遥感影像的地形C校正,考虑到反射角可能造成的影响,本文在C校正模型的基础上加入了反射角,对C校正模型进行了改进;利用高分一号的宽视场相机拍摄的16 m分辨率的200 km幅宽的遥感影像对改进的方法进行了验证,证明了反射角确实对校正结果有着比较大的影响,并且将校正结果与余弦模型和传统的C模型进行了比较,发现校正后影像的方差有所降低,阴阳坡亮度值趋于一致的趋势更加明显。
二、改进的地形校正模型
1. C校正模型
C校正模型[2]是朗伯体模型,其假定地表具有朗伯体反射特性,即地表是一理想散射反射体,入射太阳辐射在各个方向和任意波长具有均等反射可能性。除了入射太阳辐射,地表像元接收到的辐射还包括邻近地形的散射辐射和天空漫散射辐射,因此C校正中引入参数C用来描述大气和邻近地形对像元的散射辐射的贡献,从而减弱余弦校正中的过校正问题。研究表明,对于任意波段影像的像素DN值和其对应的太阳入射角余弦值都遵循线性关系[3]。
在斜面上,像素亮度值与光照系数(太阳入射角余弦值)满足关系式
LT=a+b·cosi
(1)
式中,LT为校正前影像斜面的亮度值;i为斜面的太阳入射角;a和b是通过LT与cosi的关系拟合出的直线的截距和斜率。太阳入射角i与像元的地理经纬度、太阳高度角和方位角,以及像元的坡度和坡向有关系,计算公式为
cosi=cosθSZcosθS+sinθSZsinθScos(φS-φA)
(2)
式中,i为太阳入射角;θSZ为太阳天顶角;θS为像元坡度角;φS为太阳方位角;φA为像元坡向角。
对于水平面,太阳入射角就是太阳天顶角,其像素亮度值与光照系数的关系式为
LH=a+b·cosθSZ
(3)
式中,LH为水平面的像元亮度值。
将倾斜地面的直线投影到水平地面的直线,即
即可得到C校正模型的方程
(4)
式中,参数C是根据像元亮度值与光照系数之间的统计相关性,由线性回归拟合得到的斜率b和截距a可计算得到C=a/b。
参数C并没有明确的物理含义,但根据像元受到的散射辐射随着拟合出来的截距a的增大而增大,通常可见光波段比红外波段的C值要大一些,因为可见光波段的波段短,受到大气和邻近地形的散射辐射更严重[4]。C校正模型简单易行,并且在一定程度上避免了低光照区域的过校正,可以对遥感影像有比较好的地形校正效果。
可以注意到,式(1)中表达的是地表像元在地面处接收到的辐射。但是地表像元在地面处接收到的辐射还需要经过反射才能到达传感器,因此式(1)并不能很好地对传感器接收到的辐射进行表示。当影像幅宽比较宽时,由于影像覆盖范围比较广,景内像元的最左端和最右端的反射角的大小就会有比较大的差异。而当卫星不是星下点成像时,传感器和地表像元连线与地表像元天顶线形成的反射角不再为0,这对景内像元的反射角的影响也是不可忽视的。因此有必要考虑反射角,从而更好地模拟到达传感器处的辐射量。
2. 加入反射角的改进模型
(1) 加入反射角的模型原理
传感器接收到的辐射包括以下几部分:地表像元反射的太阳直射辐射、邻近地形的散射辐射、天空漫散射辐射及程辐射[4]。由于是相对地形校正,校正的目的主要是消除影像亮度值与太阳入射角的关系,即校正太阳直射辐射的部分,而邻近地形的散射辐射、天空漫散射辐射及程辐射这3个量对于传感器接收到的总辐射来说是加性辐射量,因此统一将这3个辐射量作为一个变量a来表示。成像时刻太阳直射辐射在大气下层的辐射量为b;考虑到成像时刻的太阳天顶角,则到达地表像元的太阳直接辐射量为b·cosi;考虑到像元的反射角,基于地表反射是朗伯体的假定,地表像元接收到的辐射在像元与传感器连线这一反射方向上,实际被地表像元反射的太阳辐射则表示为b·cosi·cose。
因此,在斜面上,传感器接收到的总辐射表示为
LT=a+b·cosi·coset
(5)
式中,LT为校正前影像斜面的亮度值;i为斜面像元的太阳入射角;et为斜面像元的反射角;a和b的求解与C校正模型中的类似,是通过LT与cosi·coset的关系,拟合出的直线的截距和斜率。
类似的,在水平面上,传感器接收到的总辐射表示为
LH=a+b·cosθSZ·coseh
(6)
式中,LH表示水平面像元的亮度值;θSZ表示太阳天顶角;eh表示水平面的像元反射角。
将倾斜地面的直线投影到水平地面,即
即可得到以下C校正模型的方程
(7)
式中,参数C=a/b。
(2) 反射角的计算
① 平面像元反射角的计算
当卫星不是星下点成像时,卫星和地面目标的关系如图1所示[5]。
图1中,α是地面目标的天顶方向与地面目标和卫星连线方向所成的夹角,称为卫星天顶角;β是卫星的星下点(即天底)至地面目标点的张角,称为卫星星下点角。卫星天顶角与卫星的星下点角存在的几何关系,可由正弦定理表示为
(8)
式中,H为卫星飞行的平均轨道高度;R为地球半径。
由图1可知,卫星天顶角α就是地面目标像元的反射角,因此有
(9)
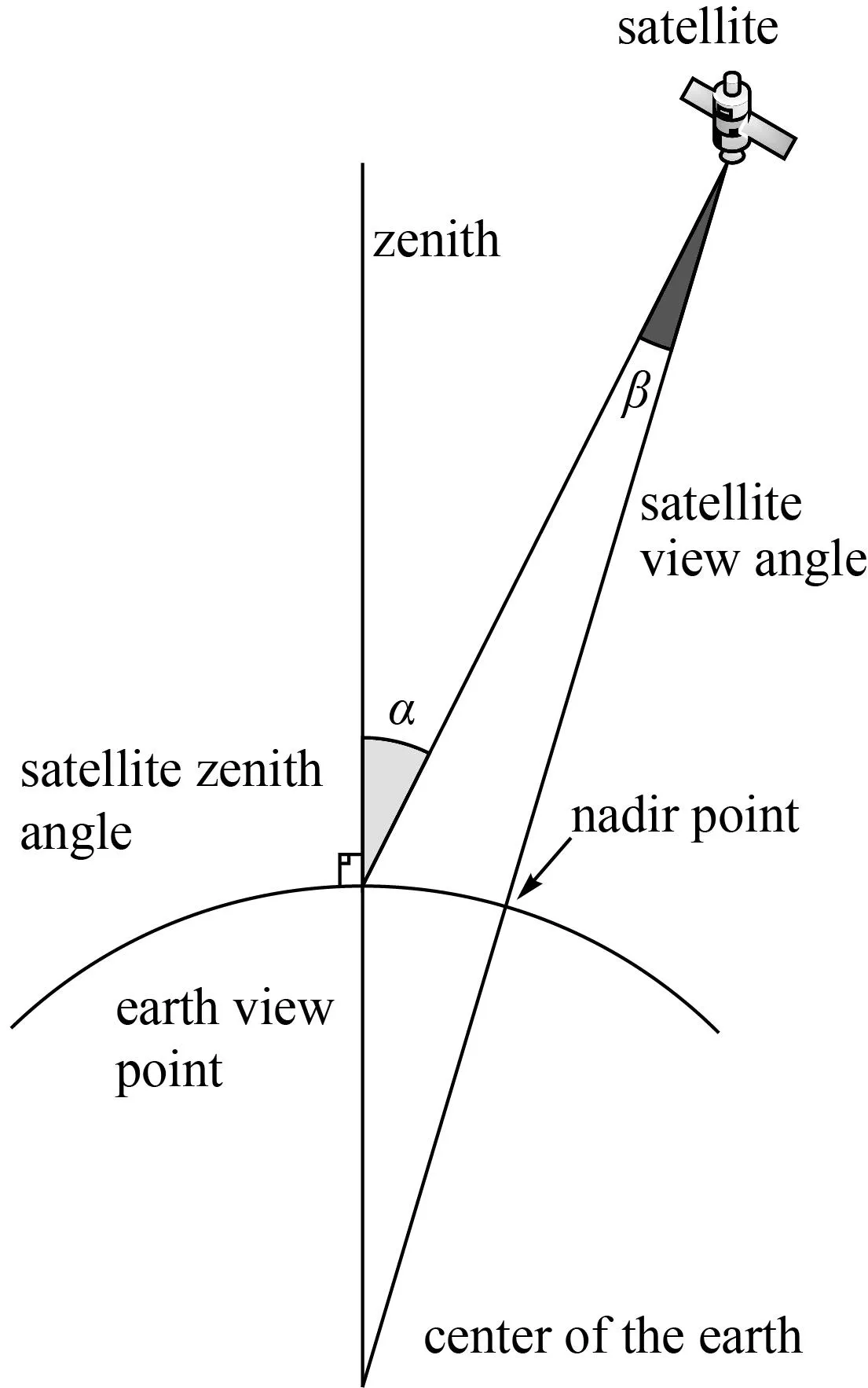
图1 卫星天顶角与地面目标星下点角的关系图
对于线阵推扫的传感器来说,传感器是垂直于卫星轨道进行推扫成像,因此在计算景内像元的星下点角时,近似认为影像上每一扫描行内的像元的星下点角的大小不同,且与其在景内的位置有关;而影像上扫描行间的相同列的像元的星下点角相同。这样只需计算通过中心像元这一扫描行上所有像元的星下点角即可得到一景内任意像元的星下点角,进一步可以得到一景内任意像元的反射角。
根据景内地面目标像元的位置差异计算每个像元的星下点角β,景内任意像元的星下点角与中心像元的星下点角的关系如图2所示。
图2中,O点表示景中心像元的位置;A表示与中心像元O同一扫描行内的任意像元A的位置;
M点是星下点;β0表示景中心像元的星下点角;β′表示像元A的星下点角。
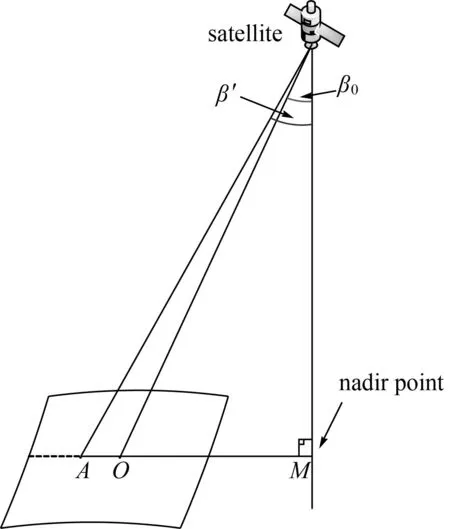
图2 任意像元星下点角与中心像元星下点角的关系图
景中心像元的卫星天顶角可以从影像的元数据中读出,记为α0,由式(7)可以计算出景中心像元的星下点角β0,进而可以近似计算出OM的距离
OM=H·tanβ0
(10)
又由像元A与中心像元O的位置关系,可以计算AO的距离,从而可以近似得到AM=AO+OM,因此像元A的星下点角β′为
(11)
再由式(8)可得任意像元A的卫星天顶角,即反射角α′。
② 斜面像元反射角的计算
图3是太阳—地面—卫星的几何关系图[6]。
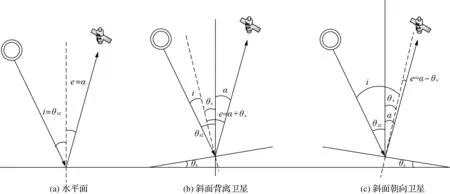
图3 太阳—地面—卫星的几何关系图
根据图3可以给出以下近似计算斜面像元反射角的关系:
图3(a)表示当地面是平面时,太阳入射角为i,θsz是太阳天顶角,卫星天顶角为α,平面像元的反射角e=α。
设卫星的方位线与坡向线所成的不大于180°的夹角为δ,图中θs表示斜面的坡度。
图3(b)表示当地面是斜面,且90°<δ≤180°时,斜面的坡向背离卫星,斜面像元的反射角e=α+θs。
图3(c)表示当地面是斜面,且0°≤δ<90°时,斜面的坡向朝向卫星,斜面像元的反射角e=α-θs。
当δ=90°时,斜面像元的反射角e=α。
综合图3(b)和图3(c)可以看出,当卫星是星下点成像时,即α=0时,水平面像元的反射角为0,斜面像元的反射角等于像元的坡度。
③ 像元平面反射角的取值范围
当遥感影像的幅宽比较宽时,像元在景内位置的差异引起的反射角的变化不容忽视。高分一号卫星的宽视场成像仪中的单相机拍摄的一景影像幅宽为200 km,平均飞行轨道高度为645 km。根据高分一号的宽视场数据的基本信息来估算一景影像内平面反射角的取值范围。
a. 当卫星是星下点成像时,如图4所示。
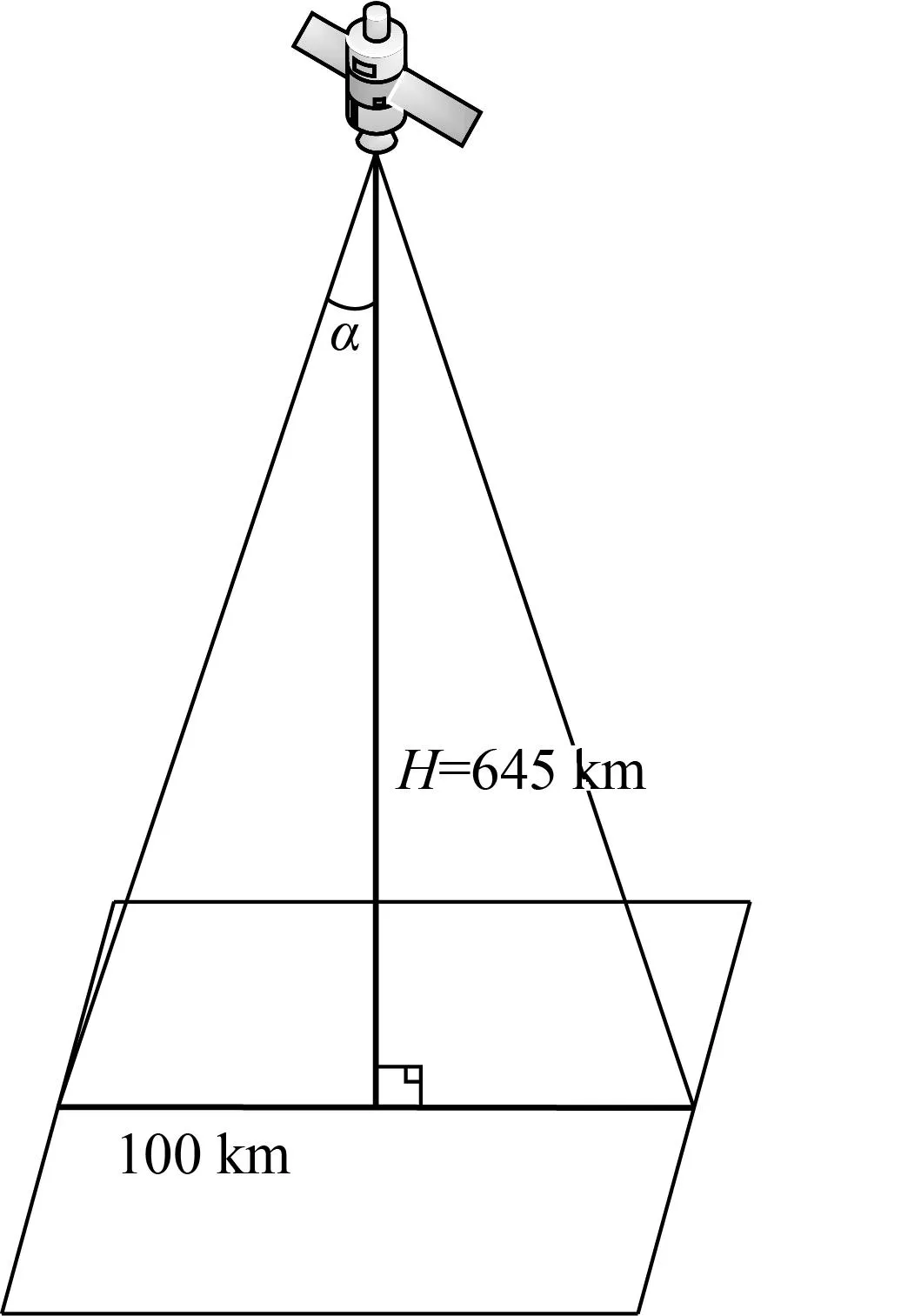
图4 卫星是星下点成像时,像元反射角示意图
通过计算可得,α的取值范围为0~8.8°,可见虽然卫星是星下点成像,但当影像幅宽比较宽时,一景影像内平面反射角的变化还是很明显的。
b. 当卫星不是星下点成像时,反射角的变化可能会更明显。高分一号卫星的宽视场的成像仪由4台相机并排组成,两两相机的主光轴之间有16°的夹角。因此在成像时并不是星下点成像的,其景中心像元的卫星天顶角α0最小可以达到0,最大可以达到30°以上。根据高分一号宽视场相机的特点,估算一景影像内平面反射角的取值范围,根据式(9)—(11)有:当α0=10°时,一景影像的像元平面反射角α的取值范围为0.3°~19.3°;当α0=20°时,一景影像的像元平面反射角α的取值范围为10.8°~28.5°;当α0=30°时,一景影像的像元平面反射角α的取值范围为21.6°~37.6°。
可以看出,当卫星不是星下点成像时,一景影像内的像元平面反射角的变化更加剧烈。因此,当对宽幅遥感影像进行地形校正,尤其是卫星不是星下点成像时,有必要将像元的反射角的影响考虑进去。
三、试验验证与分析
1. 试验数据
本文中所用的3景试验数据横跨河北、河南、山西和陕西4省,景序列号分别为153580、153595和153610,是高分一号卫星宽视场成像仪于2013年11月3日11:26(北京时间)拍摄的,其星下点地面像元分辨率优于16 m。试验所用数据是L1A级别,经过系统的辐射校正,有4个波段(红、绿、蓝、近红外),每景影像尺寸为12 000像素×13 400像素,其基本信息见表1。试验中所用的全球DEM的空间分辨率为1″(约30 m),垂直精度20 m,水平精度30 m。
2. 试验过程
1) 数据准备。根据每景影像的经纬度范围,选取同区域的全球DEM数据切片,对DEM数据进行无缝镶嵌,从而可以完全覆盖影像范围。根据影像的经纬度范围内插出每个像素的经纬度,选用的内插方法是双线性内插。通过影像覆盖区域的DEM数据,根据像素的经纬度,计算像素在DEM中的格网的行列号,得到像素的坡度和坡向。从影像元数据中可以获得成像时的太阳天顶角和太阳方位角,进一步根据式(2)计算出太阳入射角。最后根据第二章中介绍的斜面像元反射角的计算方法,计算每个像素的斜面反射角。
2) 模型验证。用景号为153580、153595和153610的3景影像,验证本文加入反射角的改进地形校正模型,直线拟合的相关系数有所提高,证明改进模型的合理性,从而可以进一步应用改进的模型对影像进行校正。
3) 校正模型。针对景号为153610的影像分别采用余弦校正[7]、C校正和本文的改进方法进行校正,比较试验结果并进行评价。
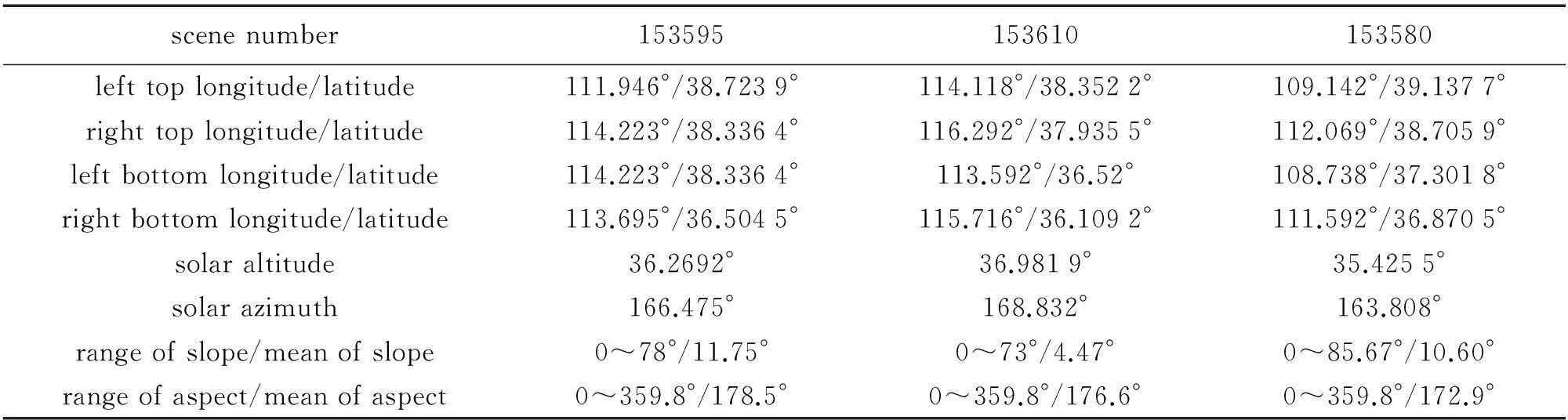
表1 试验数据基本信息
3. 试验验证与结果分析
(1) 改进的地形校正模型的合理性验证
式(1)描述的是斜面像元的亮度值与太阳入射角的线性关系,LT为因变量,cosi为自变量。对景号为153580、153595和153610的3景影像的4个波段分别应用式(1)进行最小二乘拟合,拟合出来的直线的相关系数见表2。
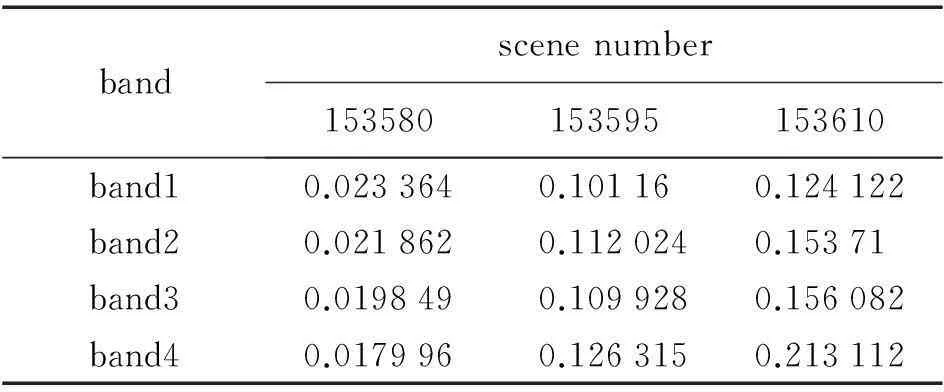
表2 根据式(1)拟合的三景影像各波段的相关系数
式(5)描述的是考虑反射角后斜面像元的亮度值与太阳入射角及像元的反射角的关系,LT为因变量,cosi·coset为自变量。对景号为153580、153595和153610的3景影像分别应用式(5)进行最小二乘拟合,拟合出来的直线的相关系数见表3。
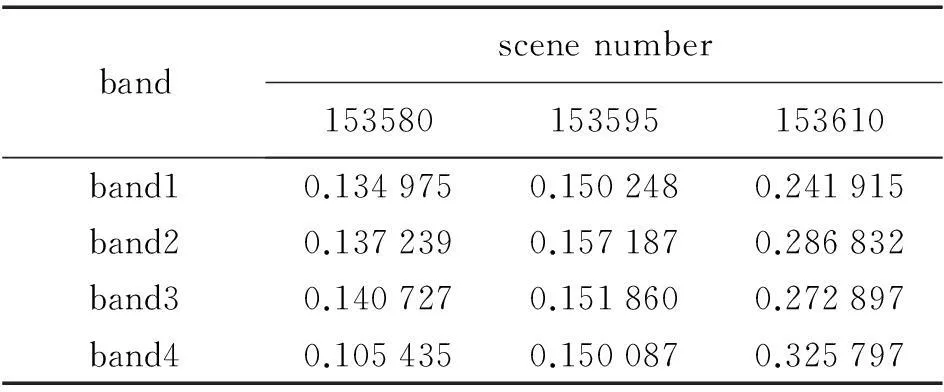
表3 根据式(5)拟合的三景影像各波段的相关系数
对比表2和表3可以看出,在模型中加入反射角的影响后,3景影像拟合出的直线相关系数有大幅度的提升。这说明影像像元的亮度值不仅与太阳入射角有关,还与像元的反射角有着密切的联系,反射角的大小对最终到达传感器处的辐射量有着很大的影响。进一步表明加入反射角的改进的地形校正模型的合理性。
(2) 改进的地形校正模型的试验结果评价
① 视觉评价
由于高分一号宽视场相机拍摄的影像尺寸比较大,因此在这里截取整景地形校正后影像中的一块影像,对这一区域影像块进行放大显示。图5(a)、(b)、(c)、(d)分别为校正前影像、余弦校正的影像、C校正的影像、改进方法校正的影像。

图5 原影像及3种方法校正后的影像图
从图5可以看出,校正前的影像有明显的地势起伏,立体感很强烈,阴坡阳坡的亮度值差异很大;校正后,3种地形校正方法基本上都达到了地形校正的效果,地形起伏对像元亮度值的影响基本上都消除了;但从余弦校正后的影像上可以看到,在太阳入射角很低的地方出现了大量的亮区,即出现过校正的现象;而在C校正和改进的校正模型的校正后影像上则没有过校正的情况。仔细对比图5(c)和图5(d)可以发现,本文的改进方法校正后影像的阴影地区的地表信息恢复得更好,阴阳坡像元的亮度值趋于一致的趋势更加明显。
② 影像统计信息评价
为了进一步对影像的校正质量进行定量的客观的评价,本文列出了影像校正后最大值、最小值、均值及标准差等统计量(见表4)。地形校正的效果越好,阴阳坡的像元的亮度值越接近,阴阳坡趋于一致的趋势更加明显,影像的标准差就更小。
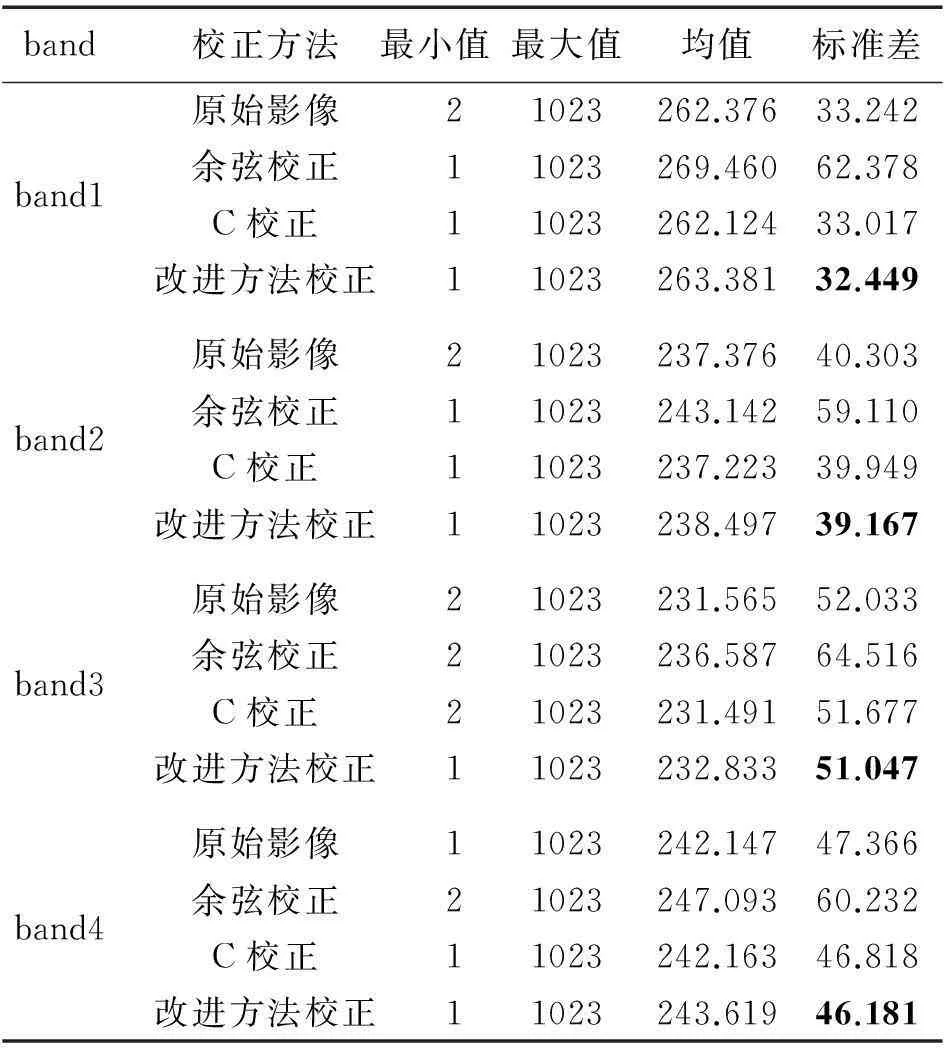
表4 原影像与3种方法校正后的影像统计量
从表4中可以看出,余弦校正的最大值和均值都明显大于未校正前的影像,校正后的影像的标准差不降反升,这是由于出现了大量的过校正现象所导致的。C校正和本文方法校正后,均值与原影像相比都没有太大的变化,而影像的标准差比原影像有所降低,说明这两种方法都使阴阳坡的像元亮度值更加接近,达到了地形校正的目的。从标准差减小的幅度来看,本文方法校正后影像的标准差减小的幅度更大,说明本文方法对地形阴影的消除、阴阳坡亮度值的均一化效果更好。
③ 像元亮度值与光照系数的相关性评价
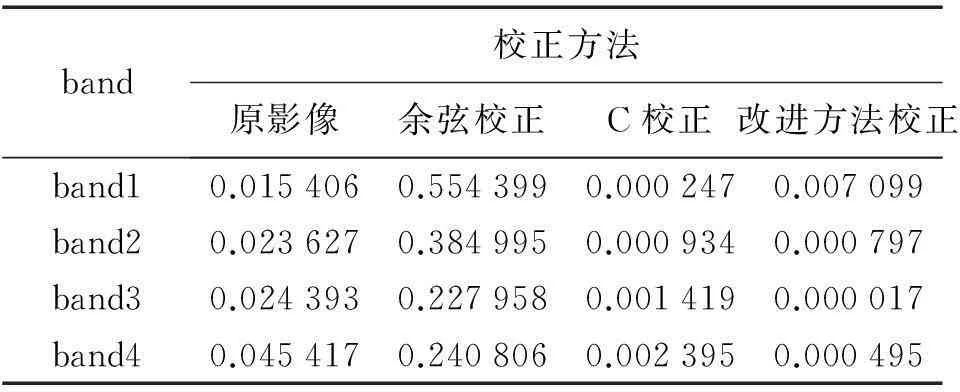
地形校正的主要目的是消除影像亮度值与太阳入射角的关系。相关系数的平方即为决定系数,决定系数的大小决定了相关的密切程度,决定系数说明模型中的自变量对因变量的影响程度。因此如果像元的亮度值不受太阳入射角的影响,则线性拟合方程的决定系数应该接近0,且越接近0说明校正的效果越好。表5列出了影像校正前和用3种方法校正后影像的各个波段的像元亮度值与光照系数的判定系数。
从表5中可以看出,余弦校正的决定系数比未校正之前要高出许多。这是因为余弦校正中出现了严重的过校正现象,在很多低光照区域出现了比原有像素亮度值高出许多的非正常像元导致的,已经出现了高度的负相关现象。C校正和本文方法校正后的决定系数比未校正之前都要小,说明两种方法降低了相关的密切程度,模型中光照系数对影像亮度值的影响程度降低。比较C校正模型和本文方法,除了第一波段,本文方法在其他几个波段的决定系数均小于C校正模型,而且第一波段的决定系数也非常接近0,说明整体上本文方法是优于C校正模型的。
表5原影像与3种方法校正后的影像的各波段拟合决定系数
band校正方法原影像余弦校正C校正改进方法校正band10.0154060.5543990.0002470.007099band20.0236270.3849950.0009340.000797band30.0243930.2279580.0014190.000017band40.0454170.2408060.0023950.000495
四、结论
1) 本文针对线阵推扫传感器的成像特点,给出了像元平面反射角及斜面反射角的计算方法,对卫星星下点成像时和非星下点成像时的平面反射角的范围进行了估算,利用多景影像验证了反射角对到达传感器处的辐射量有影响这一普遍性规律。
2) 本文模型是在C校正的模型上改进的,既保留了C校正的基本思想,又添加了反射角的影响,对非星下点成像的大场景宽幅遥感影像进行了地形校正,并从多个角度对校正结果进行了分析和评价。结果表明,本文的改进方法是合理、有效的,是优于传统的C校正的。
参考文献:
[1]刘三超, 张万昌, 蒋建军, 等. 用 TM 影像和 DEM 获取黑河流域地表反射率和反照率[J]. 地理科学, 2003, 23(5): 585-591.
[2]TEILLET P M, GUINDON B, GOODENOUGH D G. On the Slope-aspect Correction of Multispectral Scanner Data[J]. Canadian Journal of Remote Sensing, 1982, 8(2): 84-106.
[3]MCDONALD E R, WU X, CACCETTA P A, et al.Illumination Correction of Landsat TM Data in South East NSW[M].[S.l.]: Environment Australia, 2002.
[4]JENSEN J R. 遥感数字影像处理导论[M]. 陈晓玲, 龚威,李平湘,等,译.3版.北京:机械工业出版社, 2007:177-195.
[5]樊鹏山, 熊伟, 李智. 载荷侧摆情况下卫星覆盖区域计算方法研究[C]∥系统仿真技术及其应用学术会议论文集.宜昌:中国自动化学会系统仿真专业委员会,2009.
[6]GAO M L, ZHAO W J, GONG Z N et al.Topographic Correction of ZY-3 Satellite Images and Its Effects on Estimation of Shrub Leaf Biomass in Mountainous Areas[J]. Remote Sensing, 2014, 6(4):2745-2764.
[7]TEILLET P M,GUINDON B,GOODENONGH D G. On the Slope-aspect Correction of Multispectral Scanner Data[J].Photogrammetric Engineering and Remote Sensing, 1980, 9(46): 1183-1189.
引文格式: 臧熹,杨博,齐建伟,等. 一种改进的遥感影像地形校正方法[J].测绘通报,2015(1):75-80.DOI:10.13474/j.cnki.11-2246.2015.0015
作者简介:臧熹(1990—),女,硕士生,主要从事遥感影像处理方面的研究。E-mail: zx901002@sina.com
基金项目:国家973计划(2014CB744201);国家863计划(2011AA120203);国家自然科学基金(41371430;91438203)
收稿日期:2014-07-30
中图分类号:P237
文献标识码:B
文章编号:0494-0911(2015)01-0075-06

