基于深度图像的地面激光雷达与近景影像数据无缝纹理映射研究

胡春梅，李天烁，王晏民

(1. 北京建筑大学测绘与城市空间信息学院，北京 100044；

2.北京建筑大学现代城市测绘国家测绘地理信息局重点实验室，北京 100044)

Study on T-LiDAR and Close-range Imagery Data Seamless Texture

Mapping Based on Depth Image

HU Chunmei，LI Tianshuo，WANG Yanmin



基于深度图像的地面激光雷达与近景影像数据无缝纹理映射研究

胡春梅1,2，李天烁1,2，王晏民1,2

(1. 北京建筑大学测绘与城市空间信息学院，北京 100044；

2.北京建筑大学现代城市测绘国家测绘地理信息局重点实验室，北京 100044)

Study on T-LiDAR and Close-range Imagery Data Seamless Texture

Mapping Based on Depth Image

HU Chunmei，LI Tianshuo，WANG Yanmin

摘要：地面激光雷达与影像数据通过配准和纹理映射生成彩色仿真模型，但由于分辨率的差异，相邻两张影像与模型的纹理映射会出现纹理接缝现象。针对这一问题，本文以点云深度图像基准面为载体，把重叠影像投影到基准面上生成基准影像，并通过重叠基准影像的匹配对纹理接缝处进行纠正，纠正后无缝的基准影像再反投影回模型，生成无缝仿真模型。该方法解决了激光雷达与影像缝纹理接缝问题，具有一定的现实性意义。

关键词：地面激光雷达；近景影像；深度图像；纹理映射

一、引言

激光雷达与近景影像数据的配准和纹理映射可以对物体进行精细三维纹理重建，主要是按照分辨率的要求选择适合的相机和镜头，对物体进行拍照，一般根据被测物的情况拍摄多张无纹理漏洞的影像，通过激光雷达点云与影像的配准和纹理映射生成彩色仿真模型[1]，这种配准属于三维与二维的配准。目前上述配准的主要方法有：共线方程解法[2]、角锥体法[3]、直接线性变换解法[4-5]、基于罗德里格矩阵的直接解法[6-8]、单位四元数法等[9-10]、基于重心化空间相似变换模型与罗德里格矩阵联合方法加之选权迭代配准[11]等。通过比较分析，最后一种方法既满足了影像大角度的问题，又通过选权迭代提高了配准精度，但由于两种数据分辨率的差异，在点云模型与影像的纹理建模中就会出现纹理接缝现象。对于纹理接缝问题，本文将重叠部分纹理投影到基准面上生成基准影像，通过小面元微分纠正消除几何接缝，最后反投影回模型，生成无缝彩色模型。

二、点云与影像的配准

点云与影像配准是纹理建模的首要问题，本文采用基于重心化空间相似变换模型与罗德里格矩阵联合加之选权迭代的方法进行配准。应用重心化的空间相似变换模型和正交旋转矩阵与反对称矩阵的关系，得到点云与影像配准角度参数的模型。其配准模型为

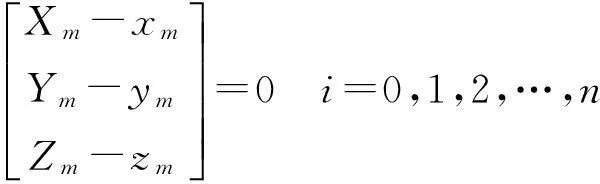
(1)

然后，应用改进的丹麦法选权迭代小粗差降权的方法对初始参数进行精确配准。改进的丹麦法权函数为

(2)

由于两种数据的分辨率差异较大，相邻影像间对于点云的纹理映射能够达到无缝，但是当影像映射到模型上生成彩色模型时，该配准精度不能得到满足，则会出现纹理接缝现象，本文以点云深度图像为中介，把重叠影像投影到其基准面上，对基准影像进行匹配和微分纠正，再反投影回模型，生成无缝彩色模型。

三、深度图像

深度图像也属于图像的一种，它遵循一般图像的格式。深度图像与一般灰度图像区别在于(如图1所示)：一般灰度图像从数学角度上只是一个二维矩阵，矩阵中每一点的元素值代表该点的灰度值g(x,y)；深度图像也是一个矩阵，所不同的是矩阵中每点的数值不再代表图像的灰度，而代表场景中可见点到某已知参考基准的距离，对于点云来说，通过点云拟合平面，对平面进行格网化，并存储点云中点到平面的距离，就生成了点云深度图像。

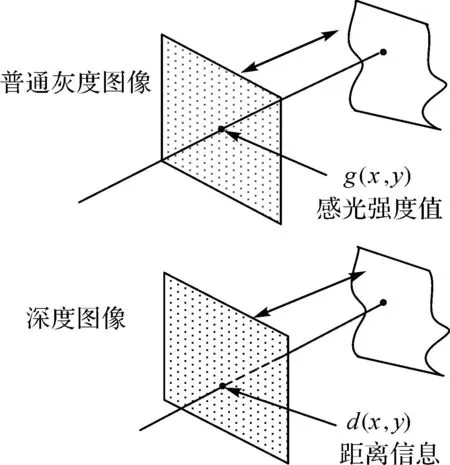
图1　灰度图像与深度图像

四、基准影像的生成

为了解决相邻影像与模型的纹理接缝问题，本文把重叠有缝部分的影像纹理投影到点云深度图像上，这是一个数字微分纠正过程。本文应用点云的深度图像模型，结合共线方程，对重叠部分影像进行微分纠正获取基准影像，其生成步骤如下：

1) 根据点云拟合基准平面，依据影像重叠区域点云确定投影范围，并以扫描分辨率设置深度图像格网点间距。

2) 计算深度图像上每个格网点的平面坐标

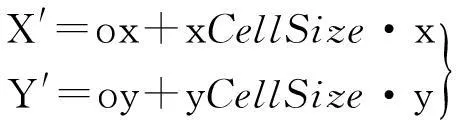
(3)

试中，(ox,oy)为点云在深度图像基准面上左下角的坐标；(xCellSize,yCellSize)为格网的间距；(x,y)为格网点坐标；(X′,Y′)为(x,y)在深度图像基准面上的坐标。

3) 根据格网点内插点云，获得每个格网点对应点云的距离值，得到格网点的三维坐标(X,Y,Z)。

4) 根据精配准得到的参数和共线方程，计算每个格网点(x,y)的纹理坐标

(4)

5) 如果(u,v)没有在整像素点上，则根据双线性内插求取其纹理值G(u,v)，把该纹理值赋给基准面格网点(x,y)。

某建筑单张影像(图2)和深度图像(图3)经过数字微分纠正生成的基准影像如图4所示。基准影像不仅记录了影像的信息，同时与模型间有着对应关系，不用把影像的信息放在模型上，利用基准影像与模型的关系进行纹理映射及可视化。对于相邻影像间的纹理接边现象，可以把相邻影像投影到同一个基准面上，在基准面上对重叠区域进行几何纠正，此过程在基准面上对影像进行了纠正，并没有改变基准影像与模型的关系，方法简单，实用性强。

图2　原始光学影像

图3　深度图像

图4　经由数字微分纠正后的影像

五、相邻基准面影像的接边

对于纹理接边，本文应用重叠部分基准面影像的密集匹配生成同名点，再应用小三角面元的几何纠正对重叠基准影像进行精确配准。

1. 基准影像的密集匹配

为了保证整体区域几何纠正的均匀性和精确性，需要对重叠区域基准影像进行密集匹配，本文选用基于均匀网格的特征点的密集匹配，基准影像是纠正过的影像，匹配相对容易。为了得到准确的匹配点对，本文采用由粗到细的金字塔匹配，金字塔层数为2层，匹配策略如下：

1) 在顶层金字塔影像上进行SIFT特征匹配，并采用RANSAC方法进行粗差剔除，并进行反向匹配，应用得到的同名点计算仿射变换参数。

2) 在底层影像上对左影像分网格进行Harris特征密集提取。

3) 应用仿射变换参数，预测左影像每一个网格点在右影像的大概位置，再应用影像相关确定右影像上的同名点。

匹配的结果中难免会有一些误匹配，在此，根据以下几何条件进行约束：

1) 目标点的顺序与同名点顺序一致。

2) 同名点的横纵坐标突变处视为粗差点进行剔除。

3) 同名点左右横坐标相差不大。

互相关是一种多峰值函数，其最大值不一定对应着同名点[12]。对于一些纹理丰富的区域，影像相关的峰值即为匹配结果；但是对于一些纹理匮乏的区域，非峰值则有可能是同名点。为了满足本文小面元的要求，对于一些相关性较弱的点，采用整体松弛法进行匹配。影像匹配算法按照执行的顺序可以分为并行算法、串行算法与松弛算法3种。松弛算法是一种并行和迭代的方法，并行处理的同时，根据迭代过程中周围点上的处理结果来调整其结果，是一种逐步逼近最优解的方法。假设左影像上的点为j，将j视为类别，共轭备选点视为目标Ai，对于左影像j，确定r个点作为j的共轭备选点，则目标集合为

(5)

假设目标Ai1、Ai2、…、Air与左影像点j的相关系数为ρ1、ρ2、…、ρr，则Aik∈Cj的概率为

Pik,j=ρk/∑ρ

(6)

假设h为i的相邻像素，k为j的相邻像素，同样计算Ph,k，计算其兼容性C(i,j;h,k)。确定了Pi,j和C(i,j;h,k)，就可以根据下列公式进行松弛法运算

(7)

式中，n(H)为相邻目标点的个数；m(K)和m(J)为从图像匹配候选点的个数；r为迭代次数，如果P(r)>T(阈值)，则停止迭代，并确定可靠的对应点。

图5为重叠区域基准面应用上述方法进行影像密集匹配的结果。

图5　基准面影像密集匹配结果

2. 密集匹配点对的三角网构建

根据重叠基准影像数据，分别提取出相邻两张图像(待纠正图像和参考图像)重叠区域的密集同名点对，然后将目标图像上的同名点构建成三角网，再将参考图像上的拓扑关系复制到待纠正图像上。三角网的构建应尽量保持三边均衡、角度均衡，应尽量防止其中一个角度过大或过小，本文采用狄洛尼三角网方法进行构网泰森多边形与狄洛尼数据文件中的N个离散点在区域E上，用一系列直线段将区域E分割为N个相邻的多边形，且满足以下条件：

1) 每个多边形内仅有一个离散点。

2) 位于多边形内的任意一点必须满足

(8)

式中，j≠i。

3) 若与其所在的两多边形的公共边上的点满足下式

(9)

式中，j≠i。满足以上3个条件的多边形称为泰森多边形,将每两邻接的多边形内的离散点用直线连接起来，所形成的三角网叫作狄洛尼三角网，泰森多边形的分法是唯一的，每个泰森多边形都是凸多边形，多边形不相交、不重叠。

六、小面元微分纠正

对上述得到的同名点建立三角网，对每一对同名的三角面片，应用小面元的仿射变换，计算变换关系式的参数，以每一个三角面片为单元进行几何纠正。仿射变换的公式如下

(10)

应用该方法得到的密集匹配点进行几何纠正，很好地解决了纹理接边问题。在纠正过程中，本文采用按三角形内插RGB的方法进行纠正，该方法的基本思想是以三角形为单元，首先将待纠正图像上的三角形的三个顶点按其变换参数纠正到目标图像上，与此同时计算每个三角形的三个顶点在待纠正图像的RGB值；然后计算出纠正后的三角形内所有像素点坐标，并使用反距离加权平均法内插出三角形内像素点的RGB值；最后根据像素点坐标及RGB值生成一副目标图像。此方法生成的目标图像质量较高、图像连续性好、方法简便。图6为纹理接缝纠正前和纠正后的对比图，从图中可以看出本文方法解决了纹理接缝的问题。

图6

七、结束语

激光雷达与多张近景影像的纹理接缝是纹理重建中的关键问题，本文应用点云与影像的高精度配准结果，通过点云的深度图像及其基准面，生成基准影像，并应用基准影像的密集匹配和小面元微分纠正技术消除纹理接缝，生成无缝的彩色仿真模型，并

应用理论和试验证明了该方法的可行性和正确性。但是，本文的研究只局限于基准面为平面的深度图像，对于复杂物体，首先要对其进行分割，按照不同基准面，如球面、柱面等基准面进行基准影像生成和纠正，这些问题将在后续的研究中解决。

参考文献：

[1]王晏民，黄慧敏，胡春梅.地面激光雷达技术在故宫保和殿数字化测绘中的应用[J]. 北京建筑工程学院学报,2012,28(3)：33-38.

[2]张剑清，潘励，王树根.摄影测量学[M].武汉：武汉大学出版社，2003.

[3]李德仁,郑肇葆.解析摄影测量学[M].北京:测绘出版社,1992.

[4]张帆.激光扫描数据三维建模中高保真度纹理重建研究[D].武汉：武汉大学，2008.

[5]冯文灏.近景摄影测量——物体外形与运动状态的摄影法测定[M]. 武汉：武汉大学出版社,2002.

[6]于志路，姚吉利，吕长广.罗德里格矩阵在空间后方交会直接解法中的应用[J].测绘工程，2005,14(2):50-52.

[7]姚吉利,孙亚廷,王树广.基于罗德里格矩阵的数码像片直接定向的方法[J]. 山东理工大学学报：自然科学版, 2006,20(2): 36-39.

[8]杨凡，李广云，王力，等. 一种基于罗德里格矩阵的最小二乘迭代坐标转换方法[J].工程勘察，2010(9)：80-84.

[9]王勇,姜挺,江刚武,等.基于单位四元数描述的单像空间后方交会[J].测绘科学技术学报，2007,24(2):133-135.

[10]江刚武,姜挺,王勇，等.基于单位四元数的无初值依赖空间后方交会[J].测绘学报，2007,36(2):169-175.

[11]王晏民，胡春梅.一种地面激光雷达点云与纹理影像稳健配准方法[J].测绘学报，2012，41(4)：267-272.

[12]孙家炳. 遥感原理与应用[M]. 武汉：武汉大学出版社，2003.

[13]闾海庆，邹峥嵘，罗发明. 近景摄影测量中旋转矩阵构成方法的研究[J].测绘科学，2007,32(3)：15-17.

[14]官云兰,程效军,周世健,等. 基于单位四元数的空间后方交会解算[J].测绘学报，2008,37(1):30-35.

引文格式： 胡春梅，李天烁，王晏民. 基于深度图像的地面激光雷达与近景影像数据无缝纹理映射研究[J].测绘通报，2015(1)：66-69.DOI:10.13474/j.cnki.11-2246.2015.0013

作者简介：胡春梅(1981—)，女，博士，讲师，主要研究方向为地面激光雷达与近景摄影测量集成。E-mail：huchunmei@bucea.edu.cn

基金项目：国家自然科学基金(41401536)；国家测绘地理信息局科技计划(2013CH-15)；北京市优秀人才培养项目(00921914013)；北京市人才强教青年英才计划(21271413106)

收稿日期：2014-08-18

中图分类号：P23

文献标识码：B

文章编号：0494-0911(2015)01-0066-04