ZY-3卫星姿态插值与拟合方法研究

范城城，王　密，朱　映，向夏芸，程宇峰

(武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉 430072)

Research on the Method of ZY-3 Satellite Attitude Interpolation and Fitting

FAN Chengcheng，WANG Mi，ZHU Ying，XIANG Xiayun，CHENG Yufeng



ZY-3卫星姿态插值与拟合方法研究

范城城，王密，朱映，向夏芸，程宇峰

(武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉 430072)

Research on the Method of ZY-3 Satellite Attitude Interpolation and Fitting

FAN Chengcheng，WANG Mi，ZHU Ying，XIANG Xiayun，CHENG Yufeng

摘要：卫星姿态作为构建ZY-3卫星高分辨率遥感影像严密几何成像模型的必要参数，其精度对卫星影像几何定位精度有直接影响，因此研究如何获取卫星成像时刻的三线阵影像扫描行精确姿态具有重要意义。本文分别基于多项式插值方法、多项式拟合方法及球面线性插值方法对ZY-3卫星星上直传精密姿态进行了拟合与平滑，进一步与基于高精度几何定标场反演的对地相机精密姿态进行了比较。研究结果表明，基于欧拉角姿态参数的插值拟合方法同样适用于四元数姿态参数，两者精度相当，且姿态拟合精度可以达到1～2角秒级，为遥感影像高精度几何处理提供精确可靠的外方位角元素。

关键词：姿态拟合；姿态插值；多项式拟合；球面线性插值；ZY-3卫星

一、引言

高精度卫星姿态是构建光学影像严密几何成像模型时重要的外方位角元素，因此ZY-3卫星遥感影像几何定位精度在很大程度上对卫星姿态质量具有依赖性。为实现ZY-3卫星精密定姿任务从而进一步保证高分辨率遥感影像的几何定位精度，星上配置了高精度星敏感器与惯性陀螺传感器，通过两者的组合定姿，可以充分保证ZY-3卫星高精度定姿任务[1]。考虑到ZY-3卫星遥感线阵影像成像时刻与卫星姿态解算时刻不一致，以及不同定姿手段、采样间隔、定姿载荷观测历元不同步等因素，需要对卫星姿态进行插值或拟合。同时，在高分卫星地面数据处理过程中，需要获取每一个扫描行的轨道和姿态数据，按照一定间隔获取的采样数据并不能在地面处理系统中直接应用，必须经过插值拟合构建合理的数学模型，从而保证高分光学卫星影像数据处理的顺利进行[2-3]。

卫星姿态常用的插值或拟合方法有Lagrange插值、连分式插值、一元全区间插值、埃特金插值、光滑插值、球面线性插值、最佳平方逼近多项式拟合及最佳一致逼近多项式拟合等[4]。对卫星姿态旋转量的插值，一般会考虑采用基于X、Y、Z轴旋转的欧拉角进行插值拟合，实践证明，由于欧拉角参数表达卫星姿态存在奇点，基于欧拉角的直接插值会导致姿态不连续性，且绕X、Y、Z轴旋转顺序的不同也会得到不同的旋转矩阵[5-6]。因此，相比于欧拉角旋转插值，姿态四元数作为卫星姿态常用描述参数，其旋转插值拟合可以得到更加连续平滑的卫星姿态，故尝试研究利用常规的插值拟合数学方法对ZY-3卫星四元数姿态参数进行数学建模具有一定意义。本文在验证ZY-3卫星星上直传精密姿态精度的基础上，分别采用最佳平方逼近多项式插值、最佳平方逼近多项式拟合、最佳一致逼近多项式拟合及球面线性插值对卫星姿态参数进行数学建模与精度评价分析，并进一步得出一些有意义的结论，为ZY-3高分遥感卫星线阵影像高精度姿态确定奠定基础。

二、相关原理

1. ZY-3卫星高精度组合定姿原理

ZY-3卫星作为我国第一颗高分辨率测绘卫星，卫星上配置的姿态敏感器包括：2台德国ASTRON10星敏感器、1台国产APS星敏感器、4组陀螺敏感器(其中1组为光纤陀螺仪)等。

ZY-3卫星星上高精度姿态解算主要是基于星载定姿传感器遥测信息，构建合理的函数模型与随机模型，采用一定的最优估计算法，精密确定卫星姿态参数，其涉及的主要处理模块包括遥测数据预处理模块、星敏感器测量模型构建模块、惯性陀螺测量模型构建模块、姿态敏感器内部特性参数标定模块、姿态敏感器相对标定与绝对标定模块、信息融合模块等。图1为ZY-3卫星星上直传高精度姿态解算流程。

图1　ZY-3卫星星上直传高精度姿态解算流程

2. ZY-3卫星对地相机精密姿态反演原理

对地相机精密姿态反演技术作为ZY-3卫星星载姿态敏感器组合定姿精度外部评价的重要手段，其主要基于对地相机高分辨率遥感影像、高精度卫星轨道及遥感影像几何定标场，构建高分辨率影像严密几何成像模型，最终反演出对地相机精密姿态参数。图2为对地观测相机精密姿态反演流程。

图2　ZY-3卫星对地观测相机精密姿态反演流程

3. 多项式插值原理

拉格朗日多项式插值作为一种常用多项式插值方法，因内插形式简单、计算速度快而被广泛应用。时刻t的ZY-3卫星姿态欧拉角参数(φ,ω,κ)可以利用其左右相邻的n个时刻外方位元素(φj,ωj,κj)，j∈[1,n]，按照如下公式内插计算

(1)

其中

除以上介绍的拉格朗日插值方法，本文涉及的多项式插值方法还包括一元全区间插值(Lgr)、一元三点插值(Lg3)、连分式插值(Pqs)、埃特金逐步插值(Atk)及光滑插值(Spl)等，主要原理与拉格朗日插值存在很多共性，故在此不再赘述。本文姿态四元数插值主要原理同上，具体按照如下公式内插计算

(2)

其中

式中，q0、q1、q2、q3表示待定时刻t姿态四元数，q0的正负号与其通过插值得到的值正负号相同。

4. 球面线性插值原理

球面线性插值(Slerp) 主要原理是构建一个函数q(t)，采用t时刻左右两端四元数q1、q2对t时刻的姿态进行确定，这样不仅会保持其单位长度不变,并且若将q1和q2看为四维空间单位球上的两个点，则Slerp将以恒定的速率扫过q1和q2之间的夹角θ。Slerp的基本原理如图3所示。

图3　四元数球面线性插值原理

单位四元数q(t)位于连接q1和q2的弧上, 与q1构成的夹角为tθ(t∈[0,1])，与q2构成的夹角为(1-t)θ(t∈[0,1]),于是q(t)可表示为q(t)=C1(t)q1+C2(t)q2。其中,C1(t)和C2(t)分别表示q(t)在q1和q2方向上分量的长度。根据图3中所示的相似三角形关系, 可以推导出C1(t)和C2(t)的表达式

(3)

则Slerp的插值函数可表示为

(4)

其中

θ=arccos-1〈q1·q2〉=

arccos-1(q10·q20+q11·q21+q12·q22+q13·q23)

如果将q1,q2看作四维空间中单位球上的两个点,Slerp将沿着连接它们的最短弧进行插值,并且能保持恒定的内插速度，可以用于高分遥感卫星姿态四元数插值。

5. 多项式拟合原理

(1) 最佳平方逼近多项式拟合

(5)

(6)

(7)

设

则

(8)

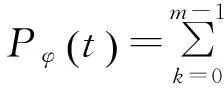
(9)

(2) 最佳一致逼近多项式拟合

(10)

满足在n个给定点上的偏差最大值为最小，即

1) 从给定的n个点中选取m+1个不同点t0、t1、…、tm组成初始参考点集。

(11)

三、ZY-3卫星姿态插值与拟合精度分析

1. 试验数据

图4　ZY-3卫星星上直传精密姿态四元数与对地相机精密姿态四元数时间序列

本文的试验数据包括由中国资源卫星应用中心提供的年积日DOY34/2012，轨道号为381的ZY-3卫星星上直传精密姿态数据，以及基于武汉大学测绘遥感信息工程国家重点实验室高分辨率光学卫星地面预处理系统软件RSOne与河南嵩山几何定标场反演的ZY-3卫星对地相机精密姿态数据。ZY-3卫星星上直传精密姿态数据弧段长度约550 s，ZY-3卫星对地相机精密姿态数据受到几何定标场范围限制，弧段长度约为1.5 s，三线阵相机高分影像定标场扫描行约5000行，姿态精度为亚角秒级。图4与图5分别表示ZY-3卫星星上直传精密姿态及对地相机精密姿态的四元数参数与欧拉角参数时间序列，从图中可以看出年积日DOY34/2012，轨道号为381的ZY-3卫星运行平稳，姿态变化缓慢，为进一步研究奠定了良好的数据基础。

图5　ZY-3卫星星上直传精密姿态欧拉角与对地相机精密姿态欧拉角时间序列

2. 试验分析

(1) ZY-3卫星姿态插值精度分析

本文首先基于四元数球面线性插值方法对ZY-3卫星上直传精密姿态精度进行验证，将DOY34/2012，轨道号为381的ZY-3卫星星上直传精密姿态数据与对地相机精密姿态数据进行对比，进一步统计姿态精度分布情况。图6表示两者姿态对比精度统计图，可以看出，ZY-3卫星上直传精密姿态精度可以达到1～2角秒级，且RMS_yaw=1.784，RMS_roll=2.474，RMS_pitch=1.020(单位均为arcsecond)，为高分遥感影像高精度对地定位提供了可靠的外方位角元素。

图6　ZY-3星上直传精密姿态与对地相机精密姿态对比精度统计

进一步讨论其他多项式插值方法的选取，分别基于一元全区间插值(Lgr)、一元三点插值(Lg3)、连分式插值(Pqs)、埃特金逐步插值(Atk)及光滑插值(Spl)对轨道号381的ZY-3卫星星上直传精密姿态数据进行最佳平方逼近多项式数学建模，并将插值结果与对地相机精密姿态数据进行比较，具体从姿态欧拉角航偏角(yaw)、滚动角(roll)及俯仰角(pitch)3个姿态方向进行统计，结果如图7—图11所示。

图7　基于一元全区间插值精度统计

图8　基于一元三点插值精度统计

图9　基于连分式插值精度统计

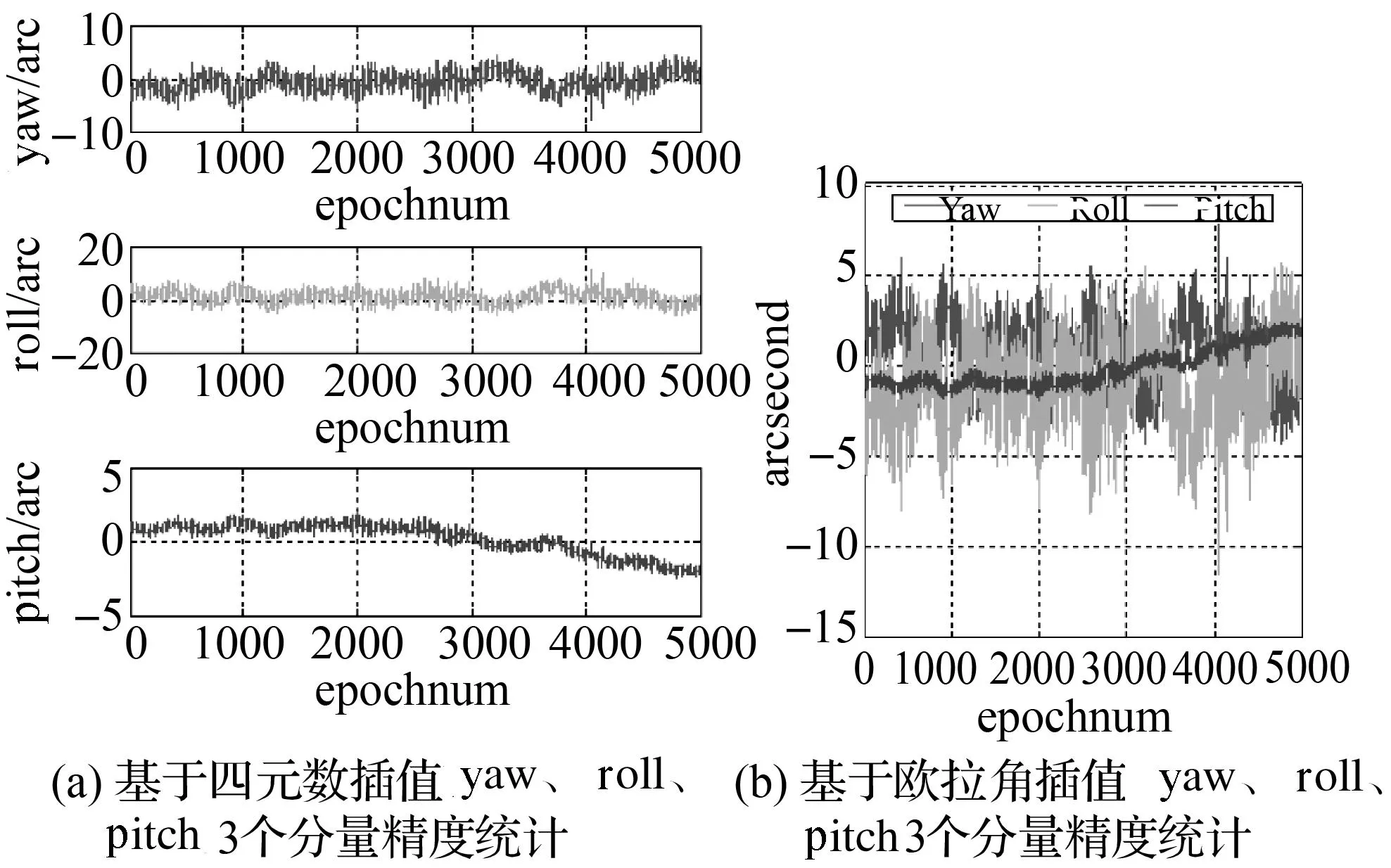
图10　基于埃特金逐步插值精度统计

图11　基于光滑插值精度统计

图7表示基于一元全区间插值，分别对四元数参数与欧拉角参数进行数学建模，通过与对地相机精密姿态比较可以看出，基于一元全区间插值方法进行姿态建模，四元数参数插值精度与欧拉角参数插值精度相当，可以达到角秒级。同样，图8表示基于一元三点插值，分别对四元数参数与欧拉角参数进行数学建模，同样可以得到很好的结果。

图9表示基于连分式插值，分别对四元数参数与欧拉角参数进行数学建模，通过与对地相机精密姿态比较可以看出，基于连分式插值方法进行姿态建模，四元数参数插值精度与欧拉角参数插值精度都不太理想，无法满足ZY-3高分线阵影像高精度姿态建模要求，故连分式插值不适合ZY-3卫星姿态参数建模。

图10与图11分别表示基于埃特金逐步插值与光滑插值，分别对四元数参数与欧拉角参数进行数学建模，通过与对地相机精密姿态比较可以看出，埃特金逐步插值与光滑插值方法可以用于ZY-3卫星姿态建模，四元数参数插值精度与欧拉角参数插值精度相当，可以达到角秒级。

表1进一步详细统计基于不同多项式插值方法，通过与对地相机精密姿态进行比较，四元数参数插值精度与欧拉角参数插值的精度分布情况。由分析可知，除连分式插值方法，一元全区间插值、一元三点插值、埃特金逐步插值、球面线性插值及光滑插值方法都可以用于ZY-3卫星姿态数据建模，四元数参数插值精度与欧拉角参数插值精度相当，且利用球面线性插值方法进行卫星姿态建模最可靠。

(2) ZY-3卫星姿态拟合精度分析

为进一步验证本文结论可靠性，分别基于最佳平方逼近多项式拟合模型与最佳一致逼近多项式拟合模型，对四元数姿态参数进行拟合分析。表2详细统计不同拟合数据个数与拟合阶次情况下最佳平方逼近多项式四元数参数拟合精度分布情况，通过分析比较可以发现，当拟合数据个数n为10～60，拟合阶次m为5～20时，最佳平方逼近多项式拟合模型可以用于ZY-3卫星姿态四元数参数数学建模，拟合精度为1～2角秒，满足ZY-3卫星高分线阵影像高精度定姿要求。

表1　基于不同多项式插值方法的姿态精度统计　arcsecond

表2　基于最佳平方逼近多项式拟合的姿态精度统计　arcsecond

图12表示基于拟合数据个数n=30,m=10最佳平方逼近多项式拟合的姿态四元数精度分布情况，由分析可以发现，航偏角(Yaw)、滚动角(Roll)及俯仰角(Pitch)3个姿态参数方向误差精度变化稳定，可以达到角秒级，进一步验证了本文的论点。

图12　基于拟合数据个数n=30,m=10最佳平方逼近多项式拟合的姿态精度统计

表3详细统计了不同拟合数据个数与拟合阶次情况下最佳一致逼近多项式四元数参数拟合精度的

分布情况，通过分析比较可以发现，当拟合数据个数n为10～60，拟合阶次m为1～2时，最佳一致逼近多项式拟合模型可以用于ZY-3卫星姿态四元数参数数学建模，拟合精度为1～2角秒，满足ZY-3卫星高分线阵影像高精度定姿要求，相比于最佳平方逼近多项式拟合模型，最佳一致逼近多项式模型用于ZY-3卫星姿态参数建模时，阶次的可选空间不大，故不太建议将最佳一致逼近多项式拟合模型用于ZY-3卫星四元数参数拟合。图13进一步验证了以上结论。

arcsecond

四、结论

本文验证了ZY-3卫星星上直传精密姿态精度，并采用多项式插值模型、多项式拟合模型及球面线性插值模型对ZY-3卫星姿态参数进行数学建模，研究结果表明：

1) 针对ZY-3卫星星上直传的精密姿态，除连分式插值方法外，一元全区间插值、一元三点插值、埃特金逐步插值、球面线性插值及光滑插值方法都可以用于ZY-3卫星姿态数据建模，四元数参数插值精度与欧拉角参数插值精度相当， 插值精度为1～2

角秒级，且利用球面线性插值方法进行卫星姿态建模最可靠。

2) 在以上结论的基础上进一步对ZY-3卫星上直传精密姿态四元数参数进行多项式拟合，试验证明相比于最佳一致逼近多项式拟合模型，最佳平方逼近多项式拟合更加适用于ZY-3卫星姿态四元数参数的建模要求，拟合精度为1～2角秒，有效保证了用于高分遥感影像高精度几何处理的外方位角元素精度要求。

致谢：感谢中国资源卫星应用中心提供的数据。

参考文献：

[1]李德仁. 我国第一颗民用三线阵立体测图卫星——资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317-322.

[2]刘军, 王冬红, 张莉, 等. 基于简化Slerp模型的三线阵影像定向片法平差[J]. 测绘科学技术学报, 2012, 29(5): 357-361.

[3]刘爱东, 黄彬, 卢中武. 基于四元数的坐标旋转与插值方法研究[J]. 计算机与现代化, 2012(2): 44-51.

[4]龚辉. 基于四元数的高分辨率卫星遥感影像定位理论与方法研究[D]. 郑州: 信息工程大学, 2011.

[5]WERTZR.SpacecraftAttitudeDeterminationandControl[M].TheNetherlands:KluwerAcademicPublishers, 1978.

[6]吕振铎, 雷拥军. 卫星姿态测量与确定[M]. 北京: 国防工业出版社, 2013.

[7]孙海燕, 李瑞明, 闫利. 机载三线阵CCD摄影中心轨迹及姿态拟合的半参数法[J]. 武汉大学学报: 信息科学版, 2003, 28(6): 706-709.

[8]GEORGEJ,TEREJANUG,SINGLAP.SpacecraftAttitudeEstimationUsingAdaptiveGaussianSumFilter[J].JournaloftheAstronauticalSciences, 2009,57(1-2): 31-45.

[9]MARKLEYFL.AttitudeDeterminationUsingVectorObservations:AFastOptimalMatrixAlgorithm[J].JournaloftheAstronauticalSciences, 1993, 41(2): 261-280.

[10]刘斌. 高分辨光学卫星空地一体化定姿及姿态抖动下影像几何处理方法研究[D]. 武汉: 武汉大学, 2011.

引文格式： 范城城，王密，朱映,等. ZY-3卫星姿态插值与拟合方法研究[J].测绘通报，2015(1)：15-21.DOI:10.13474/j.cnki.11-2246.2015.0003

通信作者：王密。E-mail：wangmi@lmars.whu.edu.cn

作者简介：范城城(1986—)，男，博士生，主要从事光学卫星影像高精度几何处理与深空导航方面的研究工作。E-mail：ccfan@whu.edu.cn

基金项目：国家973计划(2014CB744201)；国家863计划(2011AA120203)；国家自然科学基金(41371430)；长江学者与创新团队发展计划(IRT1278)

收稿日期：2014-07-30

中图分类号：P237

文献标识码：B

文章编号：0494-0911(2015)01-0015-07