卫星振动频率和振幅对高光谱成像质量影响的仿真分析和实验研究
南一冰,倪国强
北京理工大学光电学院,光电成像技术与系统教育部重点实验室,北京 100081
卫星振动频率和振幅对高光谱成像质量影响的仿真分析和实验研究
南一冰,倪国强*
北京理工大学光电学院,光电成像技术与系统教育部重点实验室,北京 100081
在星载推扫式高光谱成像仪成像过程中,卫星平台以振动为典型形式的姿态运动会导致探测器上不同的地物信息相互混叠,引起高光谱图像质量的退化。为了更有效地抑制、校正与补偿卫星振动引入的成像误差,针对典型色散型推扫成像光谱仪受平台振动而产生的空间维、光谱维质量退化的机理进行仿真分析和实验研究。通过分析其曝光时间内的光谱混合过程,得到了地物光谱和卫星姿态之间的关系,建立了推扫光谱成像退化模型。该模型综合考虑了不同姿态振动模式的影响,只要给出每个时刻的卫星平台姿态参数,即可通过普适的系数矩阵计算得出每个混合像元的平均混合比,进而获得仿真的退化高光谱数据立方体。详细推导了平均混合比的一般表达形式,对振幅、频率等振动参数对光谱混合的影响分别进行了定量分析。以实际运动状态下拍摄获得的高光谱数据立方体为例,进行了退化仿真和地面模拟运动退化实验,并对退化前后的高光谱数据进行了评价。结果表明,退化仿真和实际退化效果吻合,平均混合比能够直接反映高光谱图像退化的程度;卫星振动造成高光谱图像空间维质量恶化,使不同地物目标的光谱发生了混叠;高光谱数据的退化程度主要由振幅决定,振动频率对退化的影响较小。
卫星振动;高光谱图像;退化;光谱混合
引 言
近年来许多学者针对不同类型的成像光谱仪,研究了卫星振动对成像质量的影响。文献[1]对傅里叶成像光谱仪在轨运动成像进行了建模研究;文献[2-3]研究了卫星姿态抖动对大孔径静态干涉成像光谱仪成像质量的影响;文献[4]针对典型干涉型成像光谱仪,文献[5]针对典型色散型成像光谱仪,进行了光谱运动成像退化建模和仿真等研究。但他们的研究多是仿真分析,并没有进行真正的模拟仿真实验来验证其理论模型与真实情况的吻合程度。另外,抑制、校正与补偿卫星振动对成像质量的影响,是进行这类研究的主要目的。分析具体的空间维与光谱维的混叠过程,建立振动参数和光谱立方体数据质量之间的关系,尤其是振幅、频率等对成像质量退化的影响程度,将使我们对退化数据的校正变得有的放矢。本文推导以光栅为色散元件的成像光谱仪光谱成像退化模型,并基于实际运动状态下获取的数据,分别进行仿真和地面模拟实验,验证模型的有效性。
1 卫星平台振动
卫星振动在空域上表现为卫星本体的6个自由度上的振动,一般归纳为沿3个轴的平动和绕3个轴的转动。由于载荷离地面距离远,而对像质影响较大的主要是转动,即俯仰、侧滚和偏航三个姿态角的振动。在频域上,通常根据探测器曝光时间te和振动周期T0的比值,卫星振动可分为低频和高频振动。当te/T0<0.25时,为低频振动,在曝光时间内可等效为匀速线性运动;当te/T0≥0.25时,为高频振动,可将其看作不同谐振频率正弦运动的叠加。通常,振动频率越低振幅越大,但最大振幅一般也不超过200 μrad。振动频率范围很大,但对成像质量影响较大的主要集中在100 Hz以内[6-8]。真实的卫星振动呈现随机和复杂的特点,可能是不同频率和振幅的随机组合形式。在实际应用中,通过隔振、姿态控制等措施,可以消除100 Hz以上的高频振动。通常包括各种载荷在内的卫星平台通过总体设计,会将平台的振动基频控制在数十赫兹。由于实际振动可分解为不同基频振动的组合,本文主要针对不同基频的振动对光谱成像质量的影响开展研究。
目前主流星载成像光谱仪的地元空间分辨力(GSD)为10 m量级,曝光时间在毫秒量级,轨道高度一般在400~800 km;国内卫星平台的姿态稳定度为(10-1~10-4)°/s,国外卫星平台姿态稳定度甚至能够达到(10-6)°/s水平[9-10],由此推算卫星振动造成在曝光时间内的运动的像移一般不会超过前后左右一个像元。即实际获取的图像为每个像元DN是该像元与和其相邻行、列的8个像元DN混合的结果[4]。由于每个原始像元内都已经包含所对应地元内不同地物光谱的混合,本文在此基础上进一步研究运动成像所造成的这些不同像元之间的地物光谱混合情况。
2 光谱成像退化模型
2.1 像元混合模型
光学成像系统的物方焦距为f,在时刻t,俯仰角、侧滚角和偏航角分别为Δα,Δβ和Δθ。俯仰对成像的影响在沿轨方向上。在像面上,俯仰造成的像移在时刻t近似为Δx(t)=f·Δα(t)。同理,侧滚的影响在穿轨方向上,Δy(t)=f·Δβ(t)。偏航在沿轨和穿轨方向都有影响,但各像元在穿轨方向的像移近似为0,所以偏航的其影响主要在沿轨方向上,且影响的程度与位置有关:Δx(t)=y·Δθ(t)。由于y(半幅宽)的值通常比焦距f(高程)至少要小2个数量级,可以忽略不计。所以我们将复杂的卫星振动简化处理,主要研究俯仰和侧滚两个方向振动的影响。
狭缝以及光栅分光体制的成像光谱仪,是一类典型的推扫型成像光谱仪,可将其成像过程看作一个以狭缝为界限的二次成像过程。经前置光学系统成像(一次像面),狭缝上像点接收的辐射量为B(x,y,λ),这里x和y分别表示沿轨与穿轨(平行于狭缝)方向位置坐标,λ为波长。
在农村地区有较多养殖户存在逃避检疫的行为,由于农村地区动物防疫检疫工作缺乏有效监督管理,监督工作较为滞后。部分畜禽在检疫前均合格,长时间运输后导致其免疫力降低,运输到目的地后未能及时做好隔离观察工作,及时进行报检,将会诱发相应疫病。此外,不法分子对死因不明的动物畜禽进行贩卖,由于缺乏明确的法律规范以及市场监督,导致疫情大范围扩散[4]。
根据光栅色散原理,狭缝和探测器上像点坐标之间的几何关系如下
(1)
其中,Δλ为光谱分辨力,λmin为光谱范围最小值。
理想情况下,探测器上(二次像面)像点强度,即地物光谱,可表示为
(2)
一次像面上,实际的混合像元包括原始像元(i,j)和它的8邻域像元,根据线性光谱混合模型,混合光谱中各成分比例等于各地物在地元中所占面积之比(设各光谱段的地面反照率均匀)。因此在t时刻,混合地物光谱可表示为
(3)
其中,km, n是原始像元被偏移像元(m,n)覆盖面积的比例。
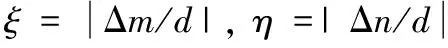
(4)
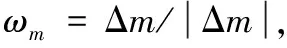
遥感探测器的曝光过程本质上是一个能量累积过程,如果卫星和地面之间在曝光积分时间te内存在相对运动,像点会沿着某一路径在像面上移动。将曝光时间N等分,如果N足够大,那么可将te内的每个小时间段内的运动当作匀速直线运动,那么最终得到的像就是每个时间段内发生像移后所成像的时间等权平均。所以,当卫星与地面存在相对运动时,探测器上像点的强度为
(5)
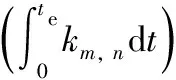
俯仰和侧滚对成像质量的影响效果非常相似,下面以俯仰姿态的振动为例,进行平均混合比的计算。为了简化计算过程,假设整个曝光过程中混合像元为(i,j)和(i+1,j),因此,Δx(t)>0,Δy(t)=0,系数矩阵K变为如下形式

(6)
假设t时刻的俯仰角为
(7)
其中,αmax为最大俯仰角度,φ为初始相位。于是,像元(i+1,j)的平均混合比如下
(8)
设te/T0=p+q,其中p∈N,q∈(0,1),式(8)变为如下形式
(9)

(10)
平均混合比的平均值可表示为
(11)
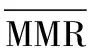
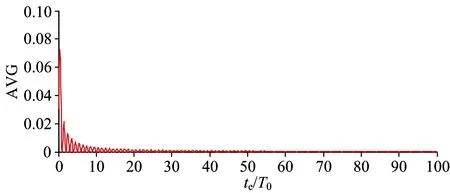
图1 AVG随te/T0的变化曲线
可以看出,当曝光时间小于振动周期时,平均混合比的值受振动频率的影响相对较大,但其对平均混合比影响的最大贡献量为7.3%,当曝光时间大于振动周期时,其影响贡献比例最大仅为2.2%,并随着te/T0值的增加,影响逐渐减小。总体来看,平均混合比的值主要由振幅决定,频率的影响很小。
2.2 平均混合比仿真计算
实际卫星振动幅度随着频率的增加而减小,表1所示为实验中使用的振动模式,包括振动频率、te/T0和对应的振幅。将其作为振动台的输入,进行光谱成像退化模拟实验。定义MMR表达式中包含频率的部分1+AVG为Cf,将表1的振动参数代入式(11),可以分别得到MMR和Cf的变化曲线,其中Cf的变化曲线间接的反映了频率对MMR值的贡献,如图2所示。可以看出,随着振动幅度的减小,MMR同时变小;而频率的变化对MMR的影响并不大。
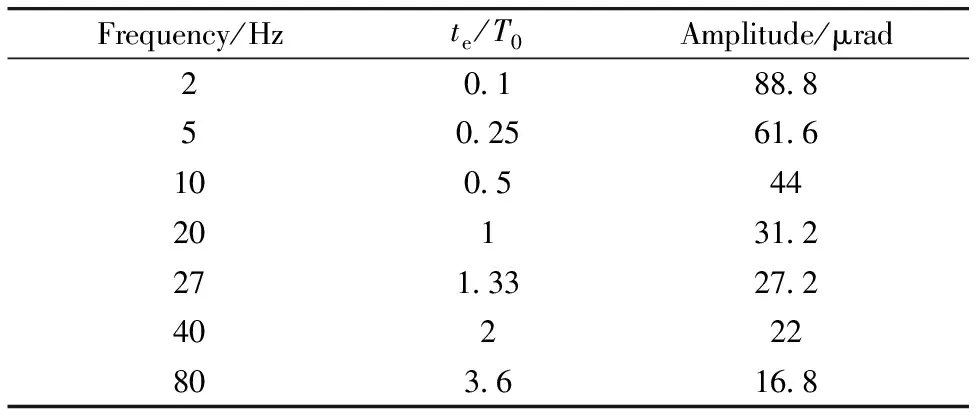
表1 实验中采用的振动模式
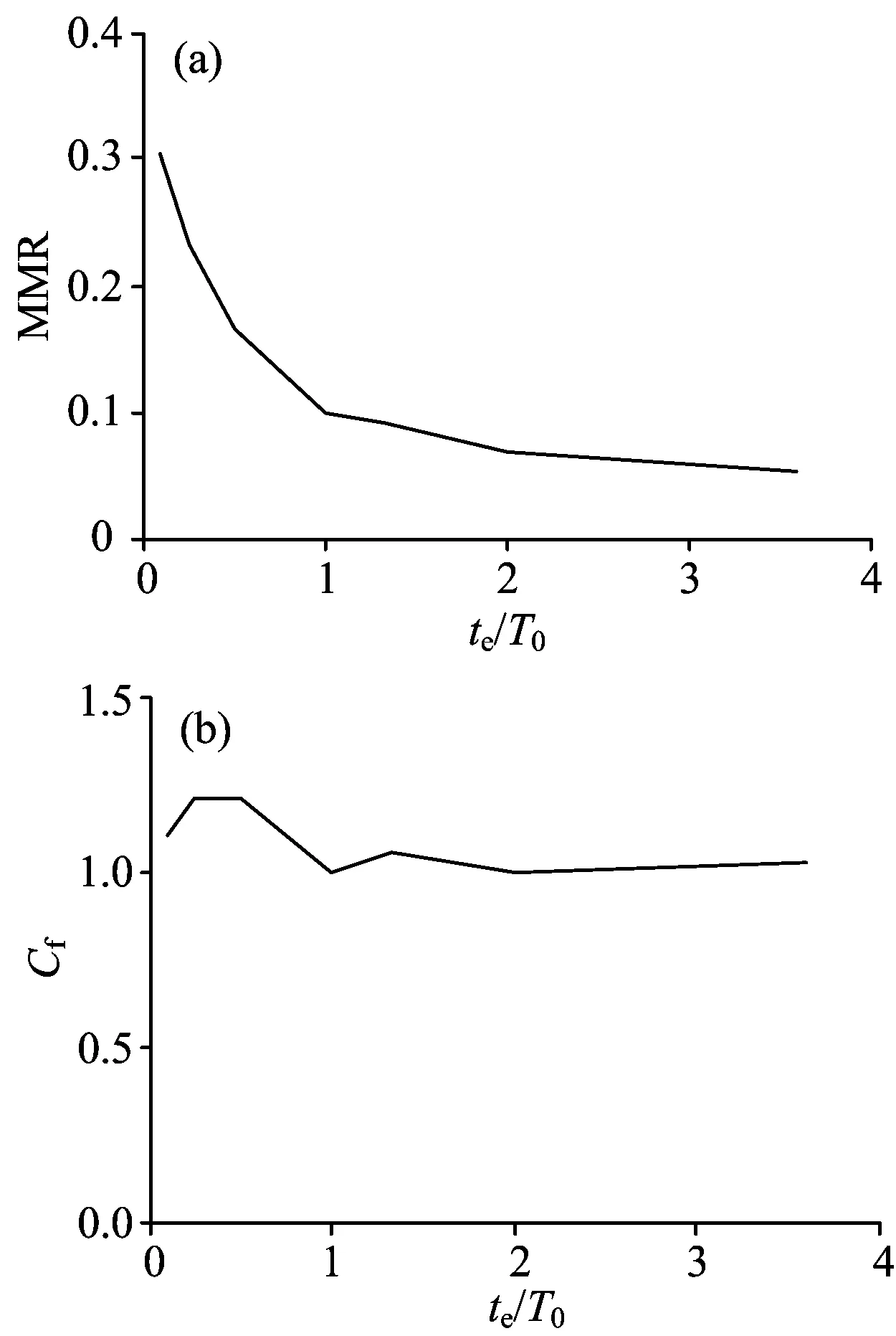
图2 MMR(a)和Cf(b)分别随te/T0的变化曲线
3 理论仿真和地面模拟实验
如图3所示,地面模拟实验系统由振动信号驱动器、带靶标的平移台、光栅尺、数字采集卡和成像光谱仪系统组成。振动信号驱动器能够输出时域位移、速度信号来控制平移台在不同时刻的位置,用户可以设置振动信号的振幅和频率,然后振动信号传输至平移台。随着振动,光栅尺和数字采集卡实时获取平移台的位移参数,然后生成振动曲线。通过调整振动参数,可以实现符合真实卫星振动的正弦振动。同时,成像光谱仪通过推扫得到探测目标的光谱数据立方体。实验中,我们获取无振动和有振动两种情况下的光谱图像。

图3 地面模拟振动实验平台
使用自研的改进型切尔尼-特纳结构成像光谱仪,首先获取两组无振动情况下的理想光谱数据立方体,以2.2节计算得到的MMR数值为基础,对其中一组理想数据进行退化处理(另一组用作参照);得到不同振动模式下,仿真的退化光谱数据立方体。同时以表1中的振动参数为地面模拟振动台的输入,通过成像光谱仪对平移台上靶板进行推扫成像(相对运动),获得实际的退化光谱数据立方体。实验中,共推扫280行,光谱数据立方体大小为500×280×165谱段。对无振动、仿真退化数据和真实退化数据进行对比评价。分别使用均方误差(mean square error,MSE)、峰值信噪比(peak signal to noise ratio,PSNR)对空间维实验结果进行评价,使用光谱信息散度(spectral information divergence,SID)、光谱相关角(spectral correlation coefficient,SCC)[11]对光谱维实验结果进行评价(图表中数值为所有波段或像元的平均值)。
由于实验采用16 bit采样,图像灰度范围为0~65 535,以te/T0=0.25为例,两组无振动图像之间的MSE为6 842,其中一组的仿真退化图像、模拟实验退化图像和无振动图像之间的MSE分别为10 588和10 842;两组无振动图像之间的PSNR为58.67,其中一组的仿真退化图像、模拟实验退化图像和无振动图像之间的PSNR分别为57.09和57.19。显然,受振动的影响,成像质量有所下降。
光谱维上,图4为仿真、模拟振动实验数据和无振动数据的SID和SCC差异。其中,仿真退化光谱、实验退化光谱的SID分别为1.2×10-4和1.2×10-3,SCC分别为0.997 2和0.968 6;从图4中可以看出,理论仿真的光谱退化效果和实际退化效果整体和局部都相吻合,说明采用MMR理论来仿真符合真实情况的光谱图像非常有效。在振动的影响下,不同地物目标的光谱发生了混叠。图5为整个视场所有点的光谱信息散度的热图,从中可以看出:地物目标较丰富或差异较大区域,其光谱混叠也相对较严重。混叠最严重和最轻微的点的光谱曲线如图6所示。

图4 仿真和模拟振动实验数据和无振动 数据的SID,SCC差异
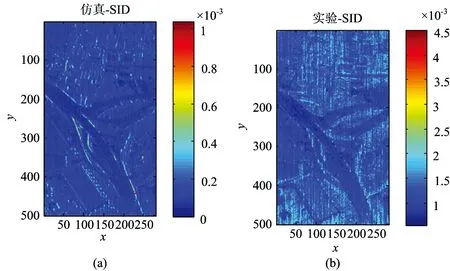
图5 仿真(a)和实验(b)中,所有点SID的热图
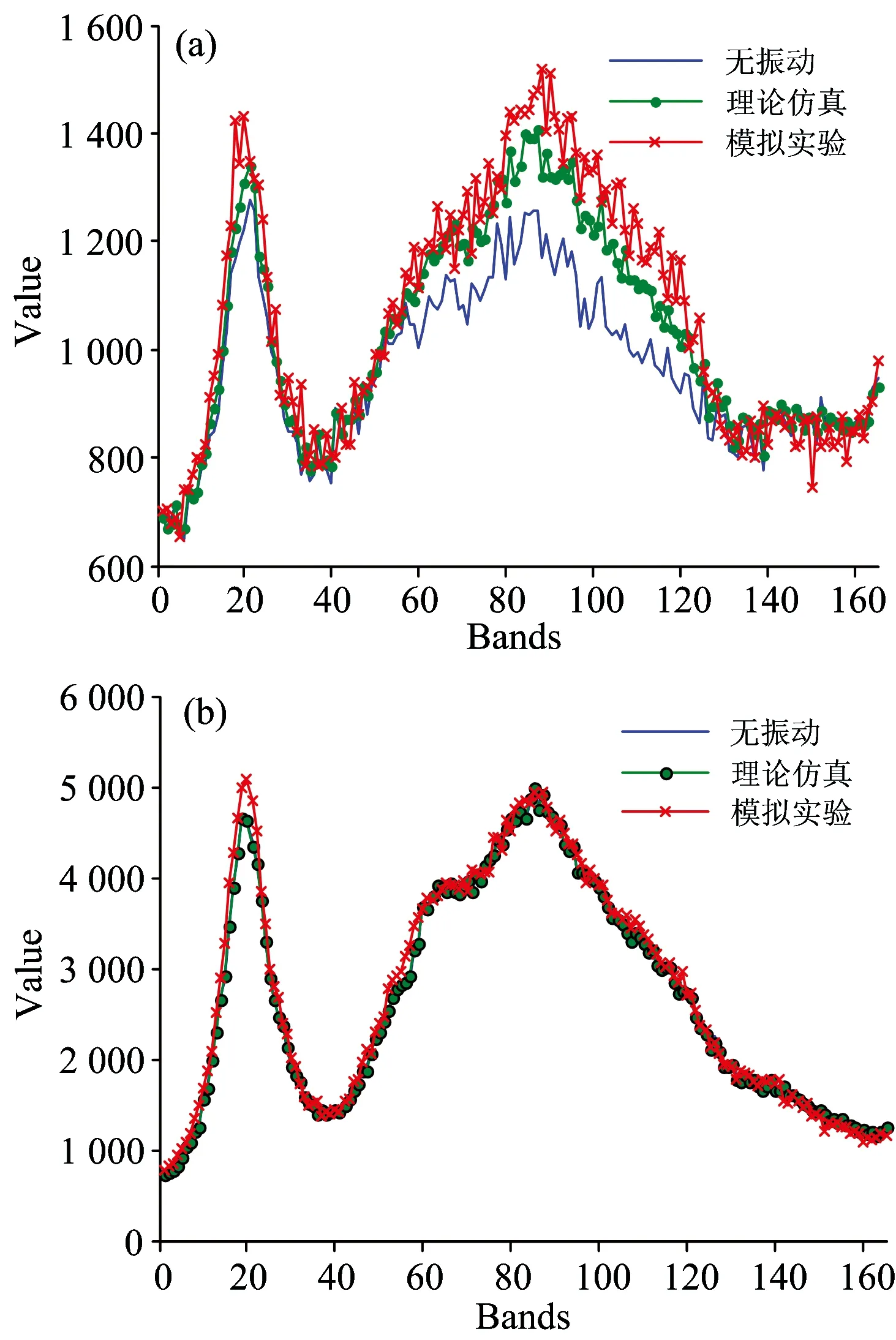
图6 光谱质量退化最严重(a)和最轻微(b)点的光谱曲线对比
对不同振动模式下的光谱图像退化情况进行评价,以分析不同振动参数对光谱成像质量的影响,评价结果如图7所示。可以看出,仿真结果和实验结果变化趋势相同;随着MMR的减小,光谱成像质量逐渐变好,成像质量和振幅以及MMR的变化趋势具有很好的相关性,光谱图像的退化程度主要由振幅决定,频率的影响非常有限。
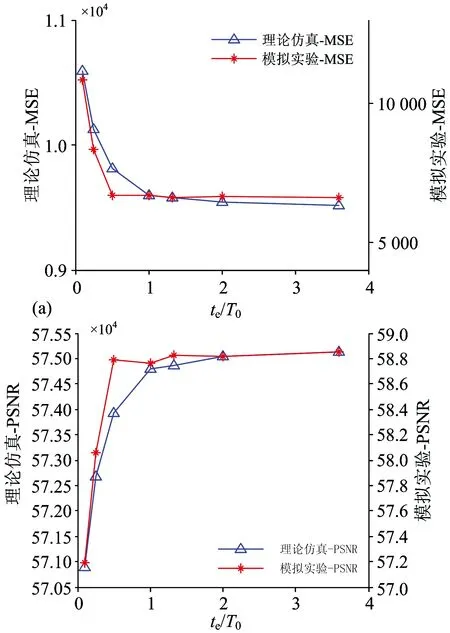
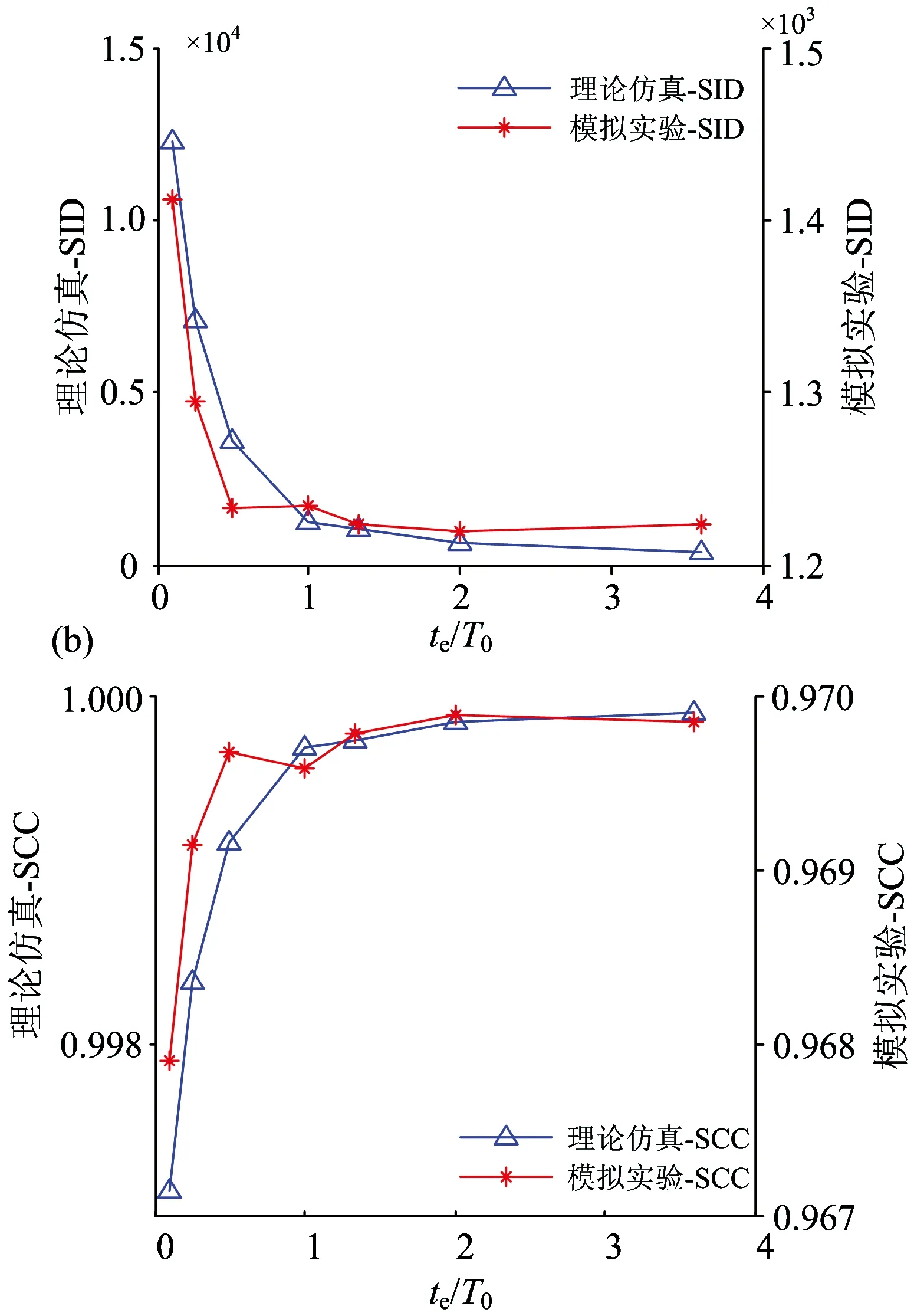
图7 数据质量退化效果
4 结 论
卫星在轨飞行过程中,包括振动在内的运动会对光谱成像质量造成影响。本文针对以光栅为分光元件的色散型成像光谱仪,建立了其推扫光谱成像退化模型,只要给出推扫过程中各时刻的卫星姿态,即可仿真出退化的光谱数据立方体。基于提出的平均混合比概念,通过定量计算不同振动参数的贡献量,得出光谱成像的退化程度主要由振动幅度决定,振动频率对退化的影响相对有限,且影响随着频率的增加而急剧下降。本文还通过仿真和地面模拟实验,验证了振动参数对光谱图像退化的影响规律和理论模型的有效性。这些成果将有助于设计更加先进有效的隔振平台,同时也有利于光谱图像校正算法的研究,从而提高光谱成像的精度。
[1] Yuan Y,Zhang X,Sun C,et al. Optik,2011,122(17):1576.
[2] YU Cheng-wei, CHEN De-rong, YANG Jian-feng, et al(余成伟,谌德荣,杨建峰,等). Opto-Electronic Engineering(光电工程),2004,31(5):4.
[3] ZHAO Hui-jie, JIA Guo-rui(赵慧洁,贾国瑞). Acta Optica Sinica(光学学报),2008,28(3):583.
[4] TANG Qiu-yan, TANG Yi, CAO Wei-liang, et al(唐秋艳,唐 义,曹玮亮,等). Acta Physica Sinica(物理学报),2012,61(7):6.
[5] Wang X,Yi T. Influence of Satellite Attitude Jitter on Dispersive Spectrometer Imaging Offset. Information. Engineering and Computer Science,2009. ICIECS 2009. International Conference on. IEEE,2009. 1.
[6] Lee S,Alexander J W,Jeganathan M. Proceedings of SPIE-The International Society for Optical Engineering,2000,3932.
[7] Xu P,Hao Q,Huang C,et al. Degradation of Image Quality Caused by Vibration in Push-Broom Camera. Photonics Asia 2002. International Society for Optics and Photonics,2002.
[8] Lieber M D. Space-Based Optical System Performance Evaluation with Integrated Modeling Tools. Defense and Security. International Society for Optics and Photonics,2004.
[9] Kramer H J. Observation of the Earth and Its Environment:Survey of Missions and Sensors. Springer,2002.
[10] BIAN Zhi-qiang, CAI Chen-sheng, LÜ Wang, et al(边志强,蔡陈生,吕 旺,等). Aerospace Shanghai(上海航天),2014,31(3):24.
[11] ZHANG Xiu-bao, YUAN Yan, WANG Qian(张修宝,袁 艳,王 潜). Acta Optica Sinica(光学学报),2011,31(5):244.
(Received Jul. 1, 2015; accepted Nov. 18, 2015)
*Corresponding author
Simulation Analysis & Experimental Study of the Effects of Satellite Vibration Frequency and Amplitude on Hyperspectral Image
NAN Yi-bing,NI Guo-qiang*
School of Optoelectronics, Key Laboratory of Photoelectronic Imaging Technology and System,Ministry of Education,Beijing Institute of Technology, Beijing 100081, China
In the imaging process of satellite-based pushbroom hyperspectral imager, attitude motions of satellite platform, represented by vibrations, will cause aliasing of the object information comes from different sub-areas of the detector, leading to degradation of hyperspectral image quality. In order to suppress and correct the imaging errors caused by satellite vibrations more effectively, spatial and spectral degradation mechanisms of typical dispersive pushbroom imaging spectrometer caused by satellite vibration are studied in this paper, including theoretical simulation and experimental study. With the analysis of spectral mixing process during exposure, the relationship between spectrum of ground object and satellite attitude is obtained, and a degradation model of pushbroom spectral imaging is presented. The effects of different attitudes of vibration are considered in the degradation model. Mean mixing ratios of each pixel are easy to calculate with a universal coefficient matrix, as long as the satellite attitude parameters of each moment are known. Then the simulation degraded spectral image data cube is achieved. The common expression of mean mixing ration is derived in detail. More important, the effects of vibration amplitude and frequency are quantitative analyzed separately. Degraded simulation and ground simulation experiments are carried out based on real hyperspectral data cubes, then the quality of the cubes before and after degradation are evaluated. Results show that simulation is in good agreement with reality. Mean mixing ratio can reflect the degradation extent of hyperspectral data directly. The satellite vibrations bring about spatial quality deteriorate of hyperspectral image, and lead to the aliasing of spectrum comes from different ground object. The degradation extent of hyperspectral data is determined mainly by vibration amplitude. The influence of frequency is limited.
Satellite vibrations;Hyperspectral image;Degradation;Spectrum aliasing
2015-07-01,
2015-11-18
国家(973计划)项目(2009CB72400504)资助
南一冰,1987年生,北京理工大学光电学院博士研究生 e-mail:ccpcnannan@126.com *通讯联系人 e-mail:nigq@bita.org.cn
TH744
A
10.3964/j.issn.1000-0593(2016)10-3226-06
- 光谱学与光谱分析的其它文章
- Gd靶激光等离子体光源离带辐射及其等离子体演化的研究
- Probing the Binding of Torasemide to Pepsin and Trypsin by Spectroscopic and Molecular Docking Methods
- Mn(Ⅱ)-5-Br-PADAP共沉淀-火焰原子吸收光谱法测定虾、贝样中的镉
- Near Infrared Spectroscopy Study on Nitrogen in Shortcut Nitrification and Denitrification Using Principal Component Analysis Combined with BP Neural Networks
- 内蒙古草原植被最大光能利用率取值优化研究
- 健康和糖尿病大鼠红细胞荧光光谱非线性程度差异

