强震作用下超高桥墩动力稳定性理论研究①

(1.延安大学建筑工程学院，陕西 延安 716000; 2.西安建筑科技大学土木工程学院,陕西 西安 710055)

强震作用下超高桥墩动力稳定性理论研究①

(1.延安大学建筑工程学院，陕西 延安 716000; 2.西安建筑科技大学土木工程学院,陕西 西安 710055)

摘要：根据平截面假定,考虑超高桥墩大位移变形产生的几何非线性影响,建立超高桥墩的振动控制微分方程,利用变步长的龙格-库塔法进行求解,结合B-R运动判定准则,对超高桥墩在地震作用下的动力失稳机理进行研究。理论分析表明,超高桥墩的动力失稳与桥墩的几何尺寸、质量分布、边界条件有密切关系;桥墩动力失稳时刻随地震波加速度峰值的增大而减小;失稳时刻与失稳加速度荷载有对应关系。算例结果表明:本文方法正确,利用本文理论能够准确计算超高桥墩的失稳时刻及失稳加速度,对超高桥墩动力失稳的理论分析及工程实践有重要指导意义。

关键词：强震作用; 超高桥墩; 动力稳定性; 位移形函数; 龙格-库塔法

0引言

随着西部大开发计划的顺利实施,在我国西南部建造了一大批超高桥墩桥梁。在地震动力荷载作用下,超高桥墩的性能失效往往由其动力稳定性控制,国内外已有对该类结构动力稳定性的研究[1-2]。但由于对结构进行动力分析时引入了时间参量,使得其动力稳定性分析变得极为困难,加之结构自身动力特性的复杂性,使得其难以用数学形式准确表达[3]。随着力学理论的发展,关于结构动力稳定分析理论不断丰富,如结构前屈状态的研判、临界荷载的确定、稳定准则的建立和结构动力失稳后结构的分析等。

孙强等[4-5]探讨了弹性介质杆在轴向荷载作用下,阻尼力对杆件稳定性的影响规律,并推导了杆件在不同边界条件下的动力分析计算公式。徐艳等[6]基于Liapunov运动稳定性定义,建立了两类结构稳定状态概念:第一类是弹性动力屈曲,通过动态特征值法进行分析研究;第二类是动力极值,利用B-R准则结合动态增量法(IDA)进行研究,其从动力稳定角度探讨了钢管混凝土拱桥的抗震性能。Bakker[7]研究了横向均布荷载作用下圆柱体的动力稳定及前屈状态。罗松南等[8-9]通过对高桥墩的简化分析,建立墩顶简支、墩底固结的压杆模型,研究分析了该桥墩模型在地震荷载和轴向冲击荷载作用下结构的动力屈曲。罗漪等[10]利用有限单元法研究了变刚度薄壁杆件在受轴向周期性作用下的动力稳定。卢皓等[11]和夏修身等[12]利用弹塑性分析方法对超高墩桥梁的高墩抗震性能及地震破坏机理进行了分析研究。李黎等[13-14]通过对结构动力分析原理进行剖析,利用有限元方法和动力特征值屈曲分析方法相结合,对设有隔震的桥梁进行了动力稳定性分析,分析结果表明该隔震桥梁动力稳定性能良好。除了在理论方面对结构动力稳定性的研究,国内外学者也通过试验手段对轴向受力杆件进行了动力屈曲研究,如孙华东[15]通过试验方法研究了圆管的轴向冲击动力屈曲。

本文根据大位移理论,通过考虑超高桥墩变形的几何非线性与结构内力的关系,建立了超高桥墩在弹性状态下动力稳定计算的二阶控制微分方程,结合变步长的Runge-kutta法研究了超高桥墩的动力响应。根据B-R判定准则,对超高桥墩在强震作用下结构的动力失稳破坏机理进行了研究分析。算例的数值计算结果表明,本文方法正确,根据本文理论能够准确预测超高桥墩的失稳时刻及其对应的地震波加速度荷载。

1分析模型建立

根据超高桥墩受载变形的力学特性,将超高桥墩简化为底端与地面固结,顶端设有集中质量和有限刚度侧向支撑的均质弹性压弯杆件,地震荷载通过与地面固结的墩底输入。在地震荷载作用下,当超高桥墩发生失稳破坏时其常处于弹性受力状态,即属于小应变大位移的几何非线性问题,因而在构件变形与内力分析时,假定压弯杆件符合平截面假定。结合以上超高桥墩简化模型和分析假定,超高桥墩动力分析模型如图1所示。规定:杆件按图1向左凸弯曲为正,轴力拉为正。

图1　超高桥墩分析模型Fig.1　Super-high pier analysis model

取桥墩中心线处的纵向位移为u(z,t),横向位移v(z,t),则桥墩横截面任意点处的纵向位移和横向位移可表示为

u(x,z,t)=u(z,t)-xv′(z,t)

(1)

v(x,z,t)=v(z,t)

(2)

根据平截面假定,考虑超高桥墩大位移引起的几何非线性影响,则桥墩中轴应变可表示为

(3)

式中:α为几何非线性因子。当α=1时,为考虑几何非线性;当α=0时,为不考虑几何非线性。

利用经典杆件理论,结合杆件变形、内力的本构关系,桥墩轴力和弯矩可表示为

(4)

M(z,t)=-EIv″(z,t)

(5)

2动力控制方程

2.1超高桥墩动力微分方程

(6)

为建立结构的动力平衡方程,取桥墩z=r处截面以上部分进行内力、变形分析。图2给出了超高桥墩动力分析的计算简图。

对图2进行竖向轴力平衡分析,得到结构轴向力平衡方程

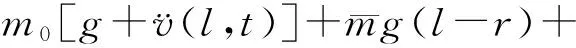
(7)

取隔离体对截面z=r处的弯矩平衡,得弯矩内力平衡方程

M(r,t)=0

(8)

将式(4)～式(6)代入式(7)、式(8)可得

(9)

(10)

式(9)和式(10)即为地震激励下超高桥墩振动的动力控制微分方程。

图2　桥墩动力分析简图Fig.2　Dynamic analysis diagram of pier

2.2边界条件

(11)

(12)

2.3初始条件

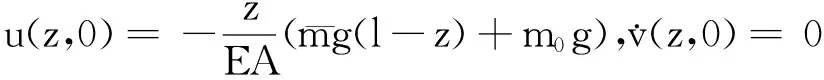
(13)

(14)

3求解方法

根据地震作用下超高桥墩振动的动力控制微分方程,结合桥墩模型的边界条件和初始条件,假设其横向和轴向位移形函数为

(15)

(16)

将式(15)和式(16)分别代入式(9)和式(10)中,化简整理可得

(17)

(18)

式中各项系数为:

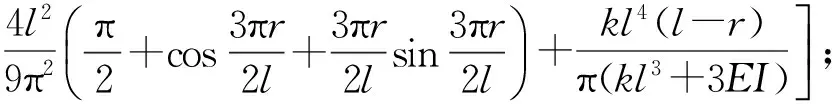
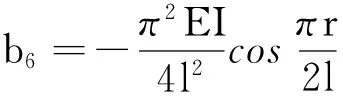
4数值算例

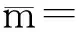
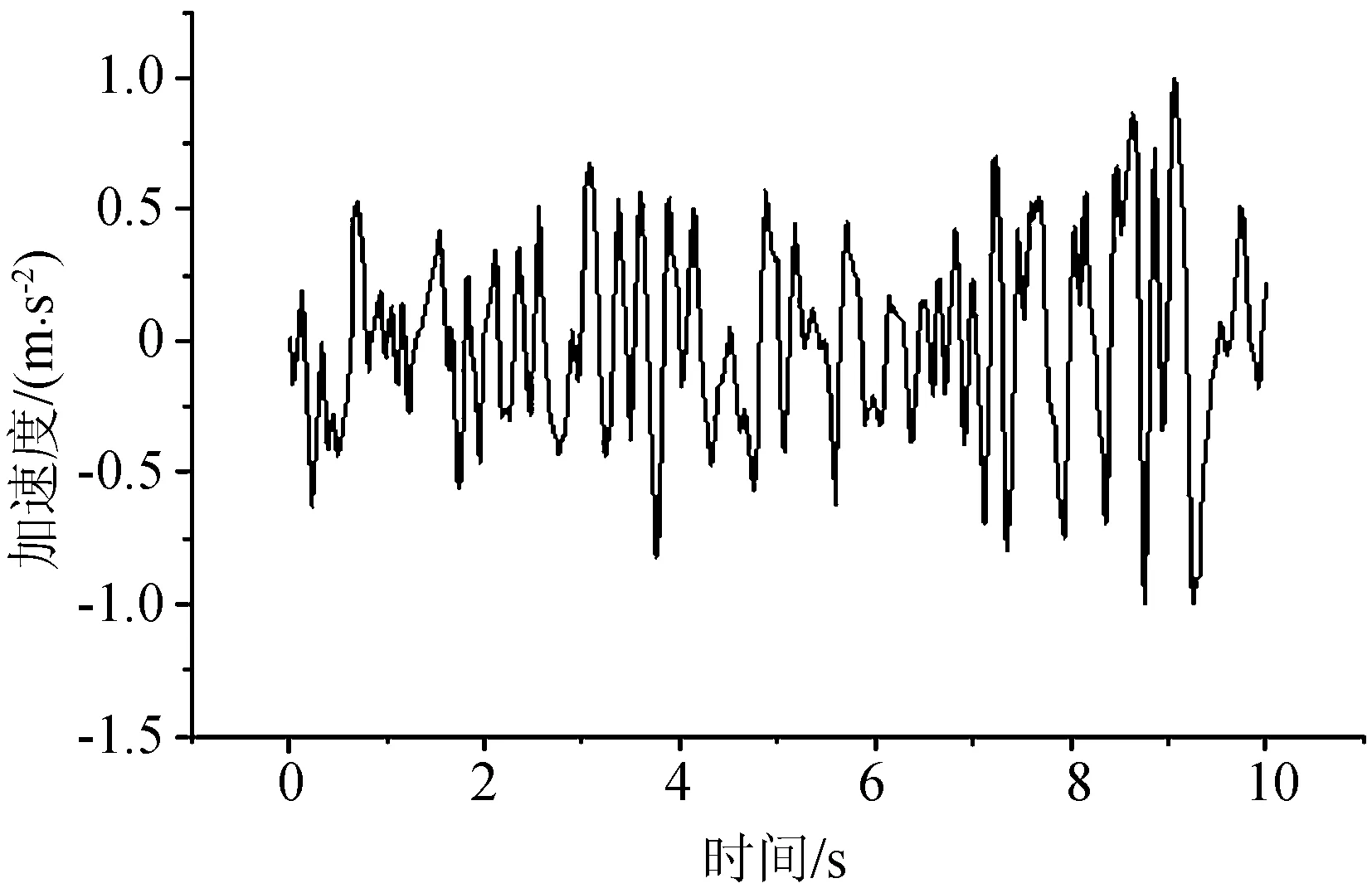
图3　归一化的部分El-Centro波Fig.3　Normalized partial El-Centro wave

为验证本文理论正确性,在较小地震荷载作用下,按照本文方法编制Matlab计算程序计算得到桥墩顶端横向位移时程,将其与利用有限元方法计算的结果进行对比。图4给出了峰值加速度为10m/s2的地震荷载作用下桥墩顶横向位移时程。由图4可知,两种方法计算结果差异较小、较为吻合,表明了本文理论的正确性。

图4　桥墩顶横向位移曲线Fig.4　Lateral displacement curve on the pier top

图5给出了各地震加速度荷载作用下结构的动力失稳时刻和加速度峰值。分析可知,在10m/s2峰值加速度荷载作用下,结构在10s内未因荷载的小幅变化而引起其位移参量的剧烈变化,即结构没有出现动力失稳现象;而在加速度峰值荷载15m/s2作用下,结构在8.6s时出现动力失稳,失稳加速度荷载为amax=11.3m/s2;在20m/s2加速度峰值荷载作用时,结构动力失稳时刻为3.06s,对应的加速度荷载为amax=12.5m/s2;将地震波加速度荷载峰值增大至25m/s2时,结构的动力失稳时刻为0.68s,失稳加速度荷载amax=12.7m/s2。

图5　墩顶位移时程曲线Fig.5　Displacement time history curve on the pier top

通过分析结构动力失稳时刻及其对应的结构失稳地震波加速度荷载值可得出以下结论:(1)该超高桥墩的动力失稳加速度在10m/s2

5结论

鉴于超高桥墩在强烈地震荷载作用下存在动力失稳的潜在危险,本文通过建立超高桥墩振动控制微分方程,利用变步长龙格-库塔法对方程求解,结合B-R运动判定稳定准则,从数值解析角度对压弯杆件进行了动力稳定性分析的理论研究。根据本文理论方法,通过编制Matlab计算程序,对算例中高柔桥墩在地震荷载作用下的动力稳定性进行了数值计算。结果表明,本文方法正确,超高桥墩的动力失稳时刻随加速度荷载峰值的增大而减小,且两者具有严格对应关系。算例分析结论表明,可根据本文方法准确预估结构失稳时刻和失稳加速度,这对超高桥墩的动力稳定研究和工程应用有重要意义。

参考文献(References)

[1]HS阿尔乔姆,L艾登.梁-柱体系在椭圆型荷载作用下的精确解和动力屈曲分析[J].应用数学和力学,2010,31(10):1249-1255.HSecilArtem,LeventAydin.ExactSolutionandDynamicBucklingAnalysisofaBeam-columnSystemHavingtheEllipticTypeLoading[J].AppliedMathematicsandMechanics,2010,31(10):1249-1255.(inChinese)

[2]王安稳.轴向冲击载荷下圆柱壳的塑性动力屈曲的问题[J].海军工程大学学报,2004,16(6):1-8.

WANGAn-wen.PlasticDynamicBucklingofCylindricalShellsunderAxialImpulsiveLoads[J].JournalofNavalUniversityofEngineering,2004,16(6):1-8.(inChinese)

[3]韩强.弹塑性系统的动力屈曲和分叉[M].北京:科学出版社,2000.

HANQiang.DynamicBucklingandBifurcationofElastic-plasticSystems[M].Beijing:SciencePress,2000.(inChinese)

[4]孙强,杨大军.弹性介质中杆的动力稳定性研究[J].工程力学,1997,14(1):87-91.

SUNQiang,YANGDa-jun.ResearchontheDynamicStabilityofPolesinElasticMedium[J].EngineeringMechanics,1997,14(1):87-91.(inChinese)

[5]孙强.伸出地而上基桩的动力稳定性研究[J].岩土工程学报,2003,25(4):459-462.

SUNQiang.AnalysisofDynamicStabilityofFoundationPileStretchingoutofGround[J].ChineseJounalofGeotechnicalEngineering,2003,25(4):459-462.(inChinese)

[6]徐艳,胡世德.地震作用下钢管混凝土拱桥的动力稳定性[J].同济大学学报:自然科学版,2007,35(3):315-320.

XUYan,HUShi-de.DynamicStabilityofConcreteFilledSteelTubularArchBridgeunderEarthquake[J].JournalofTongjiUniversity:NaturalScience,2007,35(3):315-320.(inChinese)

[7]BakkerMCM.Shear-flexuralBucklingofCantileverColumnsunderUniformlyDistributedLoad[J].JournalofEngineeringMechanics,2006,132(11):1160-1167.(inChinese)

[8]罗松南,李礼.冲击荷载下高桥墩的弹塑性动力屈曲[J].振动与冲击,2013,32(23):196-200.

LUOSong-nan,LILi.Elastic-plasticDynamicBucklingofaHighPierunderImpulseLoads[J].JournalofVibrationandShock,2013,32(23):196-200.(inChinese)

[9]罗松南,宋君晗,周慧.地基水平运动时高桥墩的动力屈曲[J].应用力学学报,2012,29(3):297-302.

LUOSong-nan,SONGJun-han,ZHOUHui.DynamicBucklingoftheHighPierundertheFoundationHorizontalMotionbyEarthquake[J].ChineseJournalofAppliedMechanics,2012,29(3):297-302.(inChinese)

[10]罗漪,王全凤.变刚度薄壁杆件的动力稳定性[J].华侨大学学报:自然科学版,2001,22(3):272-277.

LUOYi,WANGQuan-feng.DynamicstabilityofThin-walledMemberwithVariableRigidity[J].JournalofHuaqiaoUniversity:NaturalScience,2001,22(3):272-277.(inChinese)

[11]卢皓,李建中.强震作用下高墩桥梁抗震性能特点分析[J].地震工程学报,2013,35(4):858-865.

LUHao,LIJian-zhong.AnalysisofSeismicPerformanceCharacteristicsofBridgewithHighPiersunderStrongEarthquakeMotion[J].ChinaEarthquakeEngineeringJournal,2013,35(4):858-865.(inChinese)

[12]夏修身,陈兴冲,王常峰,等.高墩大跨连续刚构桥抗震性能研究[J].西北地震学报,2010,32(1):88-91.

XIAXiu-shen,CHENXing-chong,WANGChang-feng,etal.StudyonSeismicPerformanceofTall-pierandLong-spanContinuousRigid-framedBridge[J].NorthwesternSeismologicalJournal,2010,32(1):88-91.(inChinese)

[13]李黎,刘文静,张行.地震作用下隔震桥梁的动力稳定分析[J].工程力学,2010,12(增刊Ⅱ):289-293.

LILi,LIUWen-jing,ZHANGHang.AnalysisonDynamicStabilityOfisolatedBridgesSubjectedtoEarthquake[J].EngineeringMechanics,2010,12(SupplⅡ):289-293.(inChinese)

[14]李黎,廖萍,龙晓鸿,等.薄壁高墩大跨度连续刚构桥的非线性稳定分析[J].工程力学,2006,23(5):119-124,88.

LILi,LIAOPing,LONGXiao-hong,etal.NonlinearStabilityAnalysisofLong-spanContinuousRigidFrameBridgewithThin-wallHighPiers[J].EngineeringMechanics,2006,23(5):119-124,88.(inChinese)

[15]孙华东.圆管和充液圆柱壳轴向冲击动力屈曲[D].太原:太原理工大学,2000.

SUNHua-dong.DynamicBacklingofCircularTabeandFluid-filledCylindricalShellunderAxialImpact[D].Taiyuan:TaiyuanUniversityofTechnology,2000.(inChinese)

TheoreticalStudyontheDynamicStabilityofSuper-highBridgePiersunderStrongEarthquakes

CHENGMai-li1,2,LIQing-ning2,MIAORu-song2

(1.School of Architecture and Civil Engineering,Yan'an University,Yan'an 716000,Shaanxi,China;2.School of Civil Engineering,Xi'an University of Architecture and Technology,Xi'an 710055,Shaanxi,China)

Abstract：With the steady progress of transportation infrastructure construction in China,a large number of bridges with high piers have been built in the mountainous southwest region,a part of the Alpine-Himalayan seismic belt where earthquakes are frequent.Thus,research on structural seismic response has always attracted close attention.In this paper,we study the dynamic instability mechanism,seismic response,and performance of super-high bridge piers,develop reasonable structural strategies,and suggest design proposals to avoid dynamic instability.Assuming a plane section and considering the geometric non-linear effect induced by large displacement deformation of super-high piers,a numerical model of super-high piers is established.The governing differential equations of super-high piers are established,and a displacement shape function is proposed according to the force-deformation constitutive law of members.The Runge-Kutta method is used to solve the equation.Based on the B-R kinematic criterion,the dynamic instability mechanisms of super-high piers are discussed.The results from the numerical model under the dynamic conditions of various seismic waves are discussed,and longitudinal and lateral displacement at the top of high piers is studied.Theoretical analysis and calculation results show that the dynamic instability of super-high piers is closely related to pier geometry,mass distribution,and boundary conditions.The dynamic instability time of piers decreases with an increase in the peak acceleration of seismic waves.The relationship between the acceleration load and instability time shows strict correlation.The results from the example show that the method in this paper is simple,feasible,and correct.Using the theory in this paper,the dynamic instability time and acceleration load critical value of super-high piers can be calculated accurately.The theory is therefore significant in theoretical analysis and engineering practice regarding the dynamic instability of super-high piers.

Key words：strong earthquake; super-high bridge pier; dynamic stability; displacement shape function; Runge-Kutta method

收稿日期：①2015-10-15

基金项目：国家自然科学基金项目(51078306);国家青年基金项目(51408453);高等学校博士学科点专项科研基金(20106120110004);陕西省自然科学基础研究计划资助项目(2013JQ7007)

作者简介：程麦理(1987-),男,博士,主要从事桥梁结构抗震分析研究。E-mail:cml3635@163.com。

中图分类号:TU997

文献标志码：A

文章编号:1000-0844(2016)03-0360-06

DOI:10.3969/j.issn.1000-0844.2016.03.0360

程麦理1,2, 李青宁2, 苗如松2