地震动特性对隔震结构弹塑性位移反应谱的影响研究①

田英侠, 胡高兴, 李志军， 王亚楠

(西安工业大学 建筑工程学院，陕西 西安 710021)

地震动特性对隔震结构弹塑性位移反应谱的影响研究①

田英侠, 胡高兴, 李志军， 王亚楠

(西安工业大学 建筑工程学院，陕西 西安 710021)

摘要：根据特定震源机制、震级、断层距和场地条件选取69条地震动记录并进行分组，利用Nspectra软件计算隔震结构的弹塑性位移反应谱，分析断层距、场地条件、震级、阻尼比对弹塑性位移谱的影响，探讨隔震层的力学参数对地震能量耗散的影响。研究结果表明：相较于远场，处于近场的隔震结构最为不利，隔震层位移谱值受场地条件、地震加速度和速度大小影响较大；随着断层距的增大，位移谱值衰减较快，且在软土场地中隔震层的位移谱值衰减幅度大于硬土场地；地震震级大小对位移谱形状的影响不明显，但能够使隔震层的位移谱值产生整体缩放效应；阻尼比在小于0.4的范围内，隔震层在不同地震动特性作用下位移谱值差别较大，但在大于0.4以后，位移谱值及谱形基本趋于一致；屈服力较小(恢复力/重力小于等于1)的隔震层随自振周期增大其耗能性能更加突出。

关键词：隔震结构； 弹塑性位移反应谱； 地震动； 场地类别

0引言

反应谱的概念自20世纪40年代由美国学者提出以来，经过不断发展现已成为一种主要的结构抗震分析方法，并被各国抗震规范广泛采用。反应谱理论考虑了结构的动力特性和质点的地震反应加速度相对于地面运动加速度的放大作用，因而能够较为真实地反映结构受到的地震作用。但实际上很多结构在遭受较强地震动作用时可能进入塑性阶段，传统的反应谱理论是以结构反应处于线弹性范围为前提的，难以对弹塑性结构的真实地震响应做出准确的预测。上世纪六七十年代，Newmark-Hall[1-2]最早对弹塑性反应谱进行了研究，并基于等能量和等位移的准则提出了折减系数法。此后包括我国在内的一些研究者对弹塑性反应谱也进行了深入研究，如吕西林等[3]研究了结构强度、周期、场地类别对延性需求的影响，在建立恢复力特性采用黏滞阻尼滞回理论的结构分析模型的基础上研究了滞回模型参数对延性需求的影响，在基于强度折减系数法理论的基础上推算出了弹塑性位移反应谱公式；王东升等[4-5]研究了等强度的延性需求谱和强度折减系数谱的长周期特性，重点关注了等位移准则和场地条件的影响,并利用等延性强度折减系数谱间接建立的弹塑性位移谱和统计平均的弹塑性位移谱的偏差，建议了与弹性设计位移谱统计意义一致的弹塑性设计位移谱；杨伟等[6]研究了基于损伤性能的弹塑性反应谱(损伤谱)的分析方法；王丰等[7-8]研究了双向地震作用下系统的弹塑性反应谱模型，并建立了双向地震激励下系统的标准化弹塑性位移反应谱和基于统计的强度折减系数设计谱；刑朋涛等[9]提出了基于FEMA440 (2005)计算等效刚度和等效阻尼比的等效线性化方法；孙国华等[10]通过建立地震动总能量输入及滞回耗能的等效速度谱，提出了根据能量谱估算多自由度体系的能量的计算方法；何文福等[11-13]建立了关于等效阻尼比的隔震结构弹塑性反应谱，基于我国规范反应谱提出了隔震结构弹塑性反应谱公式，并研究了隔震结构设计加速度反应谱的取值，提出了隔震结构长周期段反应谱的修正公式；黄海荣等[14]基于时程分析和现有规范设计反应谱的前提，提出了铅芯隔震支座基础隔震结构的设计反应谱和位移反应谱计算公式；杜永峰等[15]针对近断层地震动具有破坏力较大的特点，研究了近断层脉动冲型地震动的速度反应谱特征，并建立了设计速度反应谱。

上述文献针对结构的各类弹塑性反应谱进行了广泛研究，但关于隔震结构弹塑性反应谱影响因素的研究较少。结构在较大的地震、风荷载等作用下可能发生非线性变形或处于非弹性状态，表现出滞回特性及刚度强度退化现象，采用符合实际的恢复力模型对于准确预测结构的非弹性响应有重要影响，尤其是对于隔震结构。结构隔震层抗侧刚度较弱，在地震动作用下会产生较大位移，为保证结构安全须将隔震层的最大位移控制在合理范围内，有必要对隔震层位移的影响因素进行研究，以便准确预测隔震层位移,为隔震结构在初步设计时的位移估算提供依据。本文根据我国现行抗震设计规范选取69条地震动记录数据，按照震级、震中距和场地条件分为9组，采用一种由理想弹塑性滞回模型、滑锁模型、非线性弹性模型和裂缝弹簧模型组合成的新型恢复力模型，计算隔震结构周期0.1～20s、阻尼比0.05～0.4的位移反应谱，探讨震级、断层距和场地类别对隔震结构弹塑性位移谱值和谱形的影响及结构恢复力参数对地震耗能的影响。

1地震动记录的选取

采用太平洋地震工程研究中心(PEER)强震数据库的地震记录数据，且统一选择震源机制为走滑断层(尽可能消除由震源机制差异的影响)。所选择地震波记录按照以下条件要求：(1)地震震级在6级以上，同一组各震级差不超过一级；(2)震源距和断层距分别在0～20，40～80和120～300km间，即处于近场、中远场和远场范围内；(3)选取场地类别为中硬土和中软土，对应的平均剪切波速(PEER地震记录通过覆土厚度超过30m时的平均剪切波速来确定)为280～500m/s和160～190m/s，分别与中国抗震规范中规定的Ⅱ类和Ⅲ类场地相对应。根据以上原则选取的地震动记录相关信息详见表1。

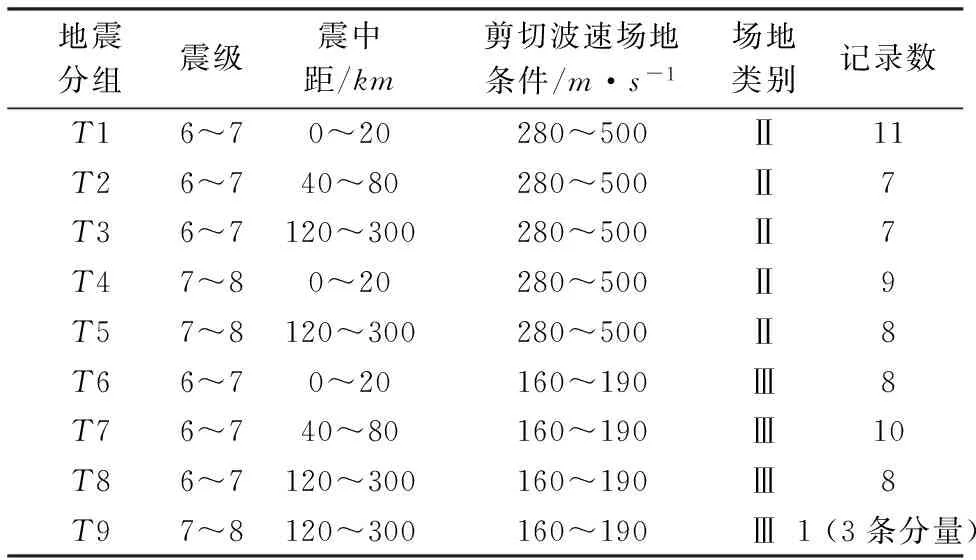
表 1　地震动记录数据信息

2计算模型及隔震层恢复力模型参数取值分析

2.1结构计算模型

单自由度体系隔震结构在地震作用下的运动方程为：

(1)

(2)

式中:ζ为体系的阻尼比；ω为体系无阻尼自振圆频率。

2.2隔震层恢复力模型

f(x)是由Ray等[16]提出的恢复力模型，其形式如图1所示。该恢复力模型基于理想弹塑性滞回模型、滑锁模型、非线性弹性模型和裂缝弹簧模型组合而成，是对Bouc-Wen模型的扩展，不仅考虑了结构屈服后刚度的强化退化及滞回曲线的捏缩效应，还考虑了结构开裂、闭合对响应或滞回性能的影响。

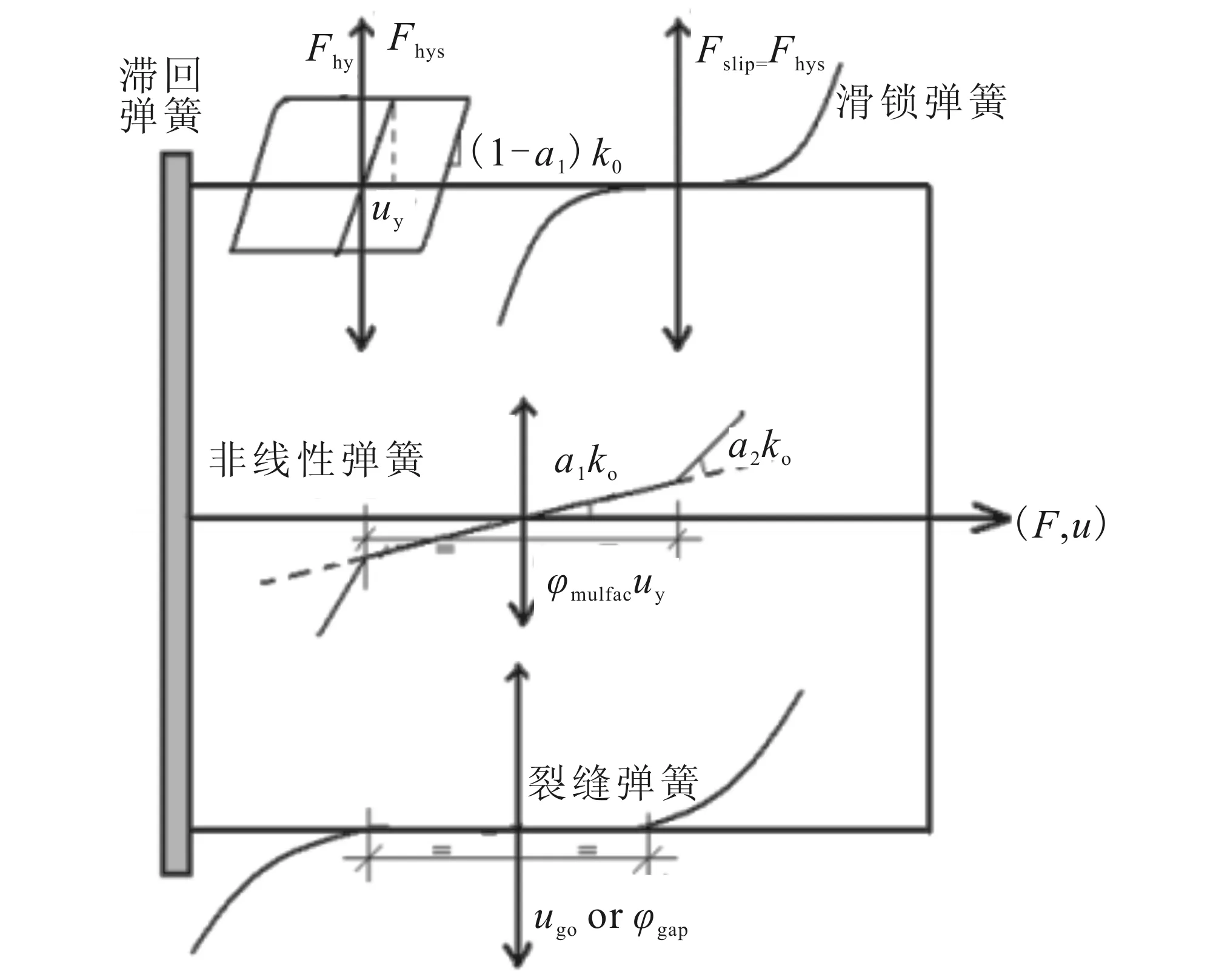
图1　隔震层恢复力模型Fig.1　Restoring force model of the base-isolated layer

现以结构在较为常用的ElCentro波作用下指定不同的滞回参数求得其滞回曲线并进行比较，分析滞回参数值对隔震结构耗能性能的影响。根据图2结果可知，当结构的PHIUP(拉力对应的位移延性系数)与PHIUN(压力对应的位移延性系数)值一定时，随着结构Fyt、Fyc(拉、压恢复力/结构重力)值的不断增大(由0.1到0.9)，结构抗震特性变化过程由处于滞回耗能充分状态到具有较大变形，且滞回曲线带有一定捏缩现象，再到结构变形出现明显的滑移现象，其抗震能力逐步减弱;当Fyt、Fyc值一定时，结构随PHIUP与PHIUN值的逐步增大表现出较大的弹塑性滑移能力；ETA(卸荷参数)在局部范围内对结构的弹塑性破坏具有一定影响。

3弹塑性位移反应谱结果

(1) 场地条件和断层距对弹塑性位移谱的影响

对于长周期结构来说，加速度反应一般较小，衰减速率也较快，不是影响隔震层响应的主要因素，相反，由于结构隔震层的刚度相对于上部结构较弱，在地震作用下隔震层处会产生较大的相对位移。图 3 给出了隔震层在T1、T2、T3、T6、T7及T8组地震作用下的平均相对位移反应谱。T1、T2、T3和T6、T7、T8两组地震集随断层距不断增大，其相应的相对位移谱值也随之明显减小，且软土场地在长周期段随断层距增大位移谱值减小的幅度远大于硬土场地。软土场地中T6、T7、T8组位移谱值分别在超过0.775s、3s和4.1s[图3(a)中三个交点]后大于T1、T2、T3，其对应的峰值分别放大了5.27倍、3.1倍和1.16倍，反映出软土场地具有使位移反应谱值增大和位移峰值对应周期延长的放大效应。且通过观察图3(b)、(c)发现，T7、T8在全周期范围内速度和加速度均小于T2、T3，说明速度和加速度并不是影响位移谱值的主要因素，而场地条件对位移谱值有很大影响，断层距是影响软土场地放大效应的主要因素。尤其在近场，软土场地的放大效应最为强烈，速度谱值和加速度谱值在长周期段分别约为硬土场地的1.5倍和4.7倍，衰减速率缓慢。

(2) 地震震级大小对弹塑性位移谱的影响

图4为T1、T8、T3和T4、T9、T5两组地震集的相对位移、速度和绝对加速度弹塑性反应谱。这两组弹塑性反应谱(包括位移、速度和加速度)形状几乎一样，仅平稳段的幅值不同，位移及速度谱值和峰值对应的周期随震级的增大而增大，在大于峰值对应的周期段内谱值基本保持平稳或衰减非常缓慢。地震震级大小对于处于近场的隔震结构的速度和位移反应谱影响很大，特别是对位移的影响最为强烈，其放大效应超过3倍，且在软土场地中这一影响将进一步扩大。

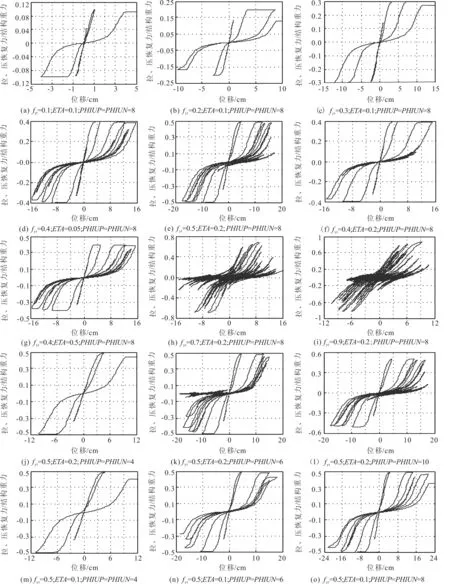
PHIUP为拉力对应的位移延性系数;PHIUN为压力对应的位移延性系数;ETA为卸荷参数图2　滞回模型不同参数对应的滞回曲线Fig.2　Hysteretic curves of the model corresponding to different parameters

图3　平均相对位移、速度及绝对加速度反应谱Fig.3　Average relative displacement,velocity,and absolute acceleration response spectrum

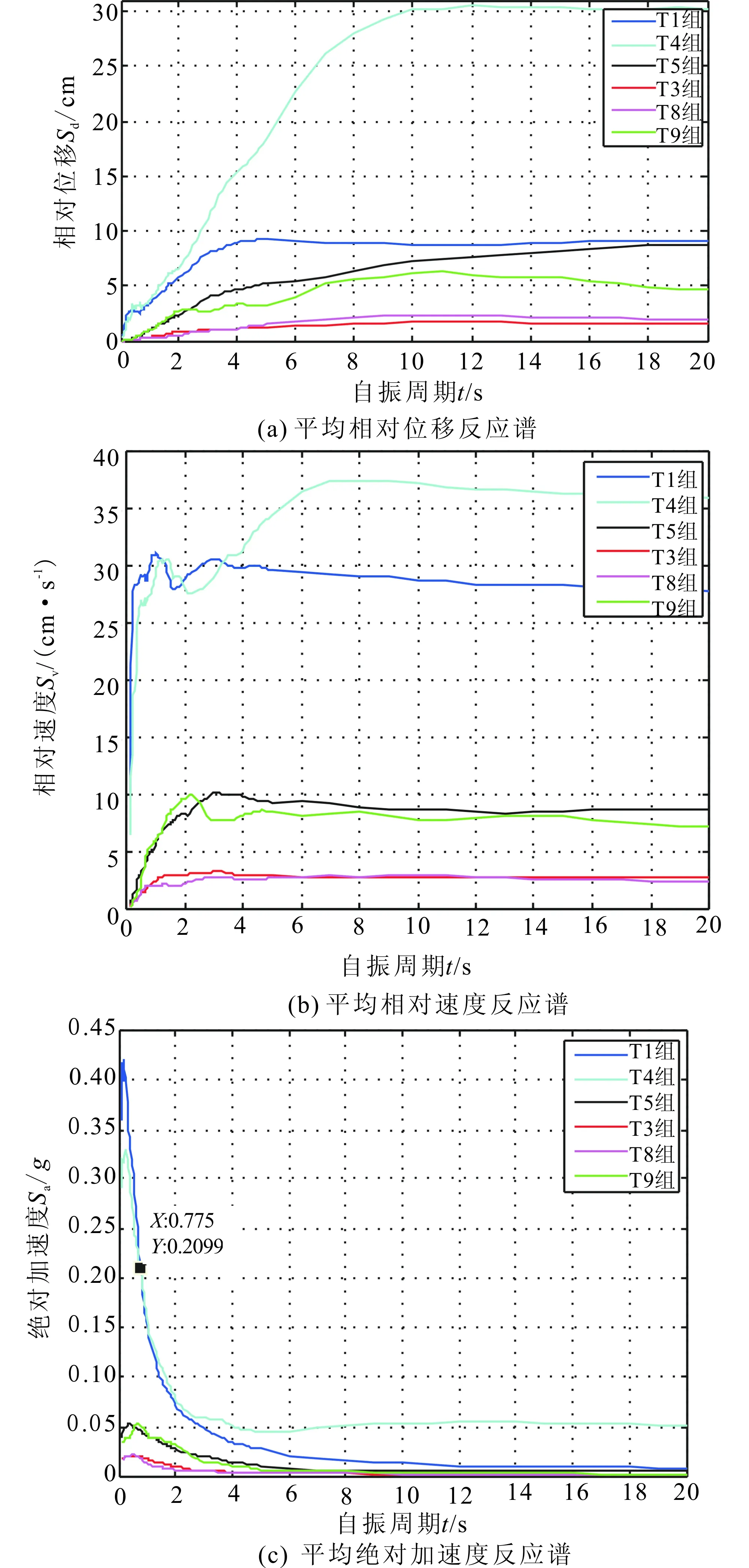
图4　两组地震集下的反应谱Fig.4　Response spectra under the action action of two groups of earthquake

隔震结构反应谱到达峰值后的位移和速度谱值随自振周期的增大基本保持水平或衰减速率非常缓慢，震级大小只影响谱值，不影响谱的形状。从图3(c)和图4(c)中的T6和T4的加速度反应谱特点可看出，在短周期范围内(小于1s)处于硬土场地的隔震结构比软土场地具有更大的加速度，但在长周期(大于1s)范围内则刚好相反。在软土场地中绝对加速度衰减至平稳段的谱值约为硬土场地的1.6倍，场地条件对其衰减至平稳段内的谱值大小具有重要影响，震级影响则较弱。处于近场中软土场地的隔震结构在周期约大于1s后绝对加速度幅值要超过硬土场地，且随震级增大此谱值超越点对应的周期值将减小。

隔震结构绝对加速度谱值在前3s内由峰值迅速衰减至一个较小值，在3s以后的长周期段内该值继续随周期缓慢衰减还是基本保持不变主要取决于场地条件及断层距。

(3) 阻尼比对弹塑性位移谱的影响

结构隔震层的阻尼比相对于一般结构而言较大，能够有效消耗地震传给结构上部的能量，减小上部结构的相对位移。图5分别给出了0.05、0.1、0.2、0.3和0.4五种阻尼比的隔震结构在T4、T6两组地震作用下的平均弹塑性位移反应谱。

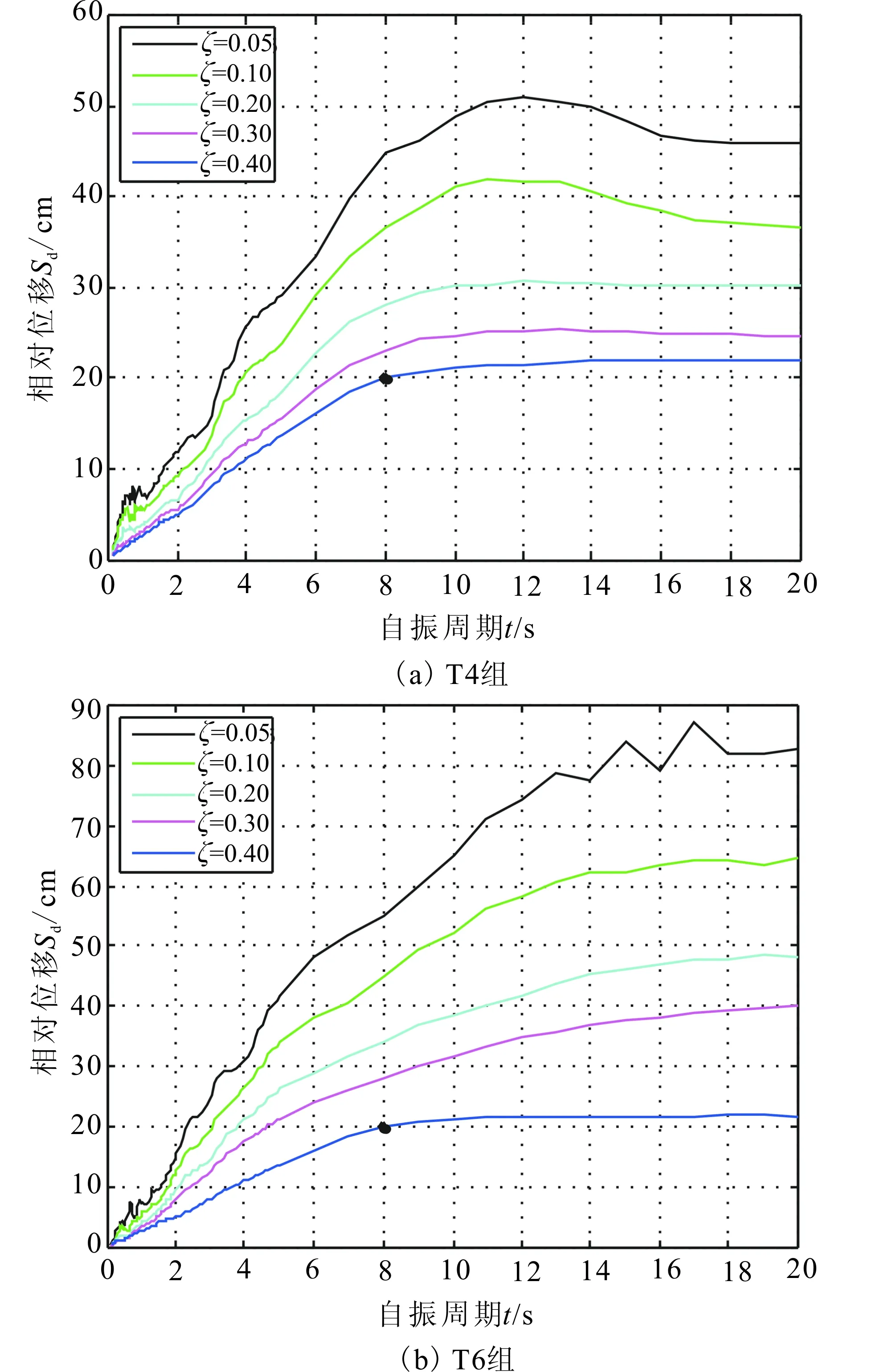
图5　T4和T6两组不同阻尼比对应的位移反应谱Fig.5　Displacement response spectrum corresponding to different damping ratio under the action of T4 and T6

从图5中可看出，随着阻尼比的不断增大，隔震层的位移谱值在长周期段内显著减小，谱形状也更加平滑，软土场地的位移谱值及衰减幅度均明显大于硬土场地。在阻尼比小于0.4时，硬土场地的位移谱值进入水平段，对应的初始周期小于软土场地，且随阻尼比增大其对应初始周期减小；而当阻尼比增大到0.4时，位移谱值进入水平段的初始点，对应周期基本相同，不同地震动特性对隔震层位移谱值及谱形的影响基本无差别。

根据以上图中各平均位移谱可看出，位移谱形状主要由上升段、平稳段、下降段和水平段(或缓慢衰减段)四部分组成，且随着场地条件、震中距和阻尼等因素的变化，位移谱的某些特征也将随之改变。

(4) 隔震层对地震耗能的影响

隔震支座不同的力学特性对隔震层地震能量耗散有重要影响，限于篇幅，图6仅给出了T6组地震动作用下隔震层随结构自振周期变化的能量耗能曲线。

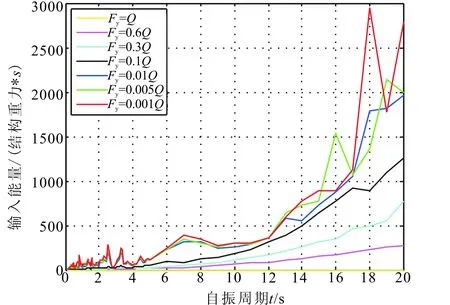
图6　隔震层耗能曲线(Q=100,Q为初始最大恢复力)Fig.6　Energy dissipation curve of isolation layer (Q=100,Q is equal to the initial maximum restoring force)

图6显示隔震层具有不同屈服力时其耗散的能量也随之改变，当结构屈服力较小(即恢复力/重力小于等于1)时，随自振周期增大隔震层耗能性能更加突出。

4结论

上述对隔震结构周期在0.1～20s之间的反应谱地震动特性分析结果，可归纳为以下几点：

(1) 场地条件对位移谱值大小及位移谱峰值对应的自振周期值具有重要影响。

(2) 断层距是影响软土场地对位移谱值产生放大效应的重要因素，同时对不同场地条件下位移谱值的衰减幅度也具有重要影响，且决定了软土场地位移谱值超越硬土场地时的周期值。地震震级大小对于处于近场的隔震结构的速度和位移反应谱影响很大，其中对位移的影响最为强烈。

(3) 隔震层的阻尼比在小于0.4范围内时，增大阻尼比能够显著减小位移谱值，不同地震动特性作用下的位移谱值差别较大，但在大于0.4以后，位移谱值及谱形基本趋于一致。

(4) 屈服力较小的隔震层随自振周期增大其耗能性能更加突出。

参考文献(References)

[1]NewmarkNM,HallWJ.ARationalApproachofSeismicDesignStandardsforStructures[C]//Proceedingsofthe5thWorldConferenceonEarthquakeEngineering,Roma,1973:2266-2277.

[2]NewmarkNM，HallWJ.EarthquakeSpec-traandDesign[M].Rerkeley:EarthquakeEngineeringResearchInstitute,1982:154-160.

[3]吕西林,周定松.考虑场地类别与设计分组的延性需求谱和弹塑性位移反应谱[J].地震工程与工程振动,2004,24(1):39-48.

LVXi-lin,ZHOUDing-song.DuctilityDemandSpectraandInelasticDisplacementSpectraConsideringSoilConditionsandDesignCharacteristicPeriods[J].EarthquakeEngineeringandEngineeringVibration,2004,24(1):39-48.(inChinese)

[4]王东升,李宏男,王国新.统计意义一致的弹塑性设计位移谱[J].大连理工大学学,2006,46(1): 87-92.

WANGDong-sheng,LIHong-nan,WANGGuo-xin.StatisticalProperty-consistentElastic-plasticDisplacementDesignSpectra[J].JournalofDalianUniversityofTechnology,2006,46(1):87-92.(inChinese)

[5]王东升,李宏男,王国新,等.弹塑性地震反应谱的长周期特性研究[J].地震工程与工程振动,2006,26(2):49-55.

WANGDong-sheng,LIHong-nan,WANGGuo-xing,etal.StudyonCharactersofLongPeriodPortionofInelasticSpectra[J].EarthquakeEngineeringandEngineeringVibration,2006,26(2):49-55.(inChinese)

[6]杨伟,欧进萍.结构地震弹塑性反应谱——损伤谱[J].地震工程与工程振动,2008,28(6):44-53.

YANGWei,OUJin-ping.EarthquakeInelasticResponseSpectra——DamageSpectra[J].EarthquakeEngineeringandEngineeringVibration,2008,28(6):44-53.(inChinese)

[7]王丰,王楠楠,张振楠,等.双向地震激励的标准化弹塑性位移反应谱[J].大连民族学院学报，2015,17(1):69-72.

WANGFeng,WANGNan-nan,ZHANGZhen-nan,etal.NormalizedElasticplasticDis-placementSpectraforBi-directionEarthquakeExcitations[J].JournalofDalianNationalitiesUniversity,2015,17(1):69-72.(inChinese)

[8]王丰,李宏男,伊廷华.双向地震作用下等延性强度折减系数反应谱研究[J].振动工程学报,2009,22(2):193-199.

WANGFeng,LIHong-nan,YITing-hua.StrengthReductionFactorSpectraofConstantDuctilityFactorsforBidirectionalEarthquakeMotions[J].JournalofVibrationEngineering,2009,22(2):193-199.(inChinese)

[9]刑朋涛,梁兴文.新型框架结构弹塑性地震反应的等效线性化方法研究[J].震灾防御技术,2014，9(4):790-800.

XINGPeng-tao,LIANGXing-wen.StudyonEquivalentLinearizationMethodforElastoplasticSeismicResponseofNewFrameStructures[J].EarthquakeDisasterPreventionTechnology,2014，9(4):790-800.(inChinese)

[10]孙国华,顾强,何若全,等.基于能量反应谱的抗弯钢框架结构能量计算[J].土木工程学报,2012,45(5):41-48.

SUNGuo-hua,GUQiang,HERuo-quan，etal.EvaluationofSeismicEnergyofSteelFramesBasedonEnergySpectrums[J].ChinaCivilEngineeringJournal,2012,45(5):41-48.(inChinese)

[11]何文福,刘文光,杨骁,等.隔震结构弹塑性反应谱分析研究[J].振动与冲击,2010,29(1):30-33，42.

HEWen-fu,LIUWen-guang,YANGXiao，etal.ElastoplasticResponseSpectraofIsolatedStructures[J].JournalofVibrationandShock, 2010,29(1):30-33,42.(inChinese)

[12]刘文光,何文福,霍达,等.隔震结构设计加速度反应谱的取值研究[J].振动与冲击,2010,29(4):181-187.

LIUWen-guang,HEWen-fu,HUODa,etal.ModifiedEquationforLongPeriodofDesignResponseSpectrumofanIsolatedStructure[J].JournalofVibrationandShock,2010,29(4):181-187.(inChinese)

[13]何文福,霍达,刘文光,等.长周期隔震结构的地震反应分析[J].北京工业大学学报，2008,34(4):391-397.

HEWen-fu,HUODa,LIUWen-guang,etal.StudyonLongPeriodPortionofAccelerationDesignSpectra[J].JournalofBeijingUniversityofTechnology,2008,34(4):391-397.(inChinese)

[14]黄海荣,朱玉华.基础隔震结构反应谱研究[J].结构工程师,2010,26(3):123-129.

HUANGHai-rong,ZHUYu-hua.StudiesonDesignResponseSpectrumforBase-isolatedStructures[J].StructuralEngineers,2010,26(3):123-129.(inChinese)

[15]杜永峰,徐天妮,王亚楠，等.近断层地震动作用下设计速度反应谱研究[J].地震工程学报，2014,36(4):997-1002，1013.

DUYong-feng,XUTian-ni,WANGYa-nan,etal.AnalysisofDesignedVelocityResponseSpectraSubjectedtoNear-faultGroundMotion[J].ChinaEarthquakeEngineeringJournal,2014,36(4):997-1002,1013.(inChinese)

[16]Ray,Tathagata,Ryu,etal.SmoothHysteresisModelsinNonlinearStructuralAnalyses-implementations:IDARCVersion7.2：“TechnicalReportMCEER-11-00XX,MultidisciplinaryCenterforEarthquakeEngineeringResearch(MCEER)[M].UniversityatBuffalo(SUNY),Buffalo，2011.

InfluenceofGroundMotionCharacteristicsontheInelasticDisplacementSpectraofIsolatedStructures

TIANYing-xia,HUGao-xing,LIZhi-jun,WANGYa-nan

(College of Civil Engineering, Xi’an Technological University, Xi’an 710021, Shaanxi, China)

Abstract：Based on the specific focal mechanism, magnitude, fault distance, and site condition, 69 ground motion records are selected and grouped. Nspectra software is used to calculate the inelastic displacement response spectrum of a single isolated structure under ground motion. The influence of fault distance, field condition, magnitude, and damping ratio on the inelastic displacement spectrum is analyzed, and the influence of the mechanical parameters of seismic isolation layer on the seismic energy dissipation is discussed. The results indicate that compared with the far field, the base-isolated structure in the near field is more unfavorable. Moreover, the seismic isolation layer displacement spectrum is greatly influenced by field conditions, earthquake acceleration, and speed. With the increase of the fault distance, the attenuation of displacement spectrum values increases, and the displacement spectrum of the base isolated layer in the field of soft soil is more than that of hard soil. The influence of earthquake magnitude on the spectrum shape is not obvious; however, it can cause a scaling effected on the displacement spectrum of the base isolated layer. When the damping ratio is less than 0.4, the value of displacement spectrum of the seismic isolation layer differs largely with different ground motion characteristics; when the damping ratio is greater than 0.4, the value of displacement spectrum basically become the same. The energy dissipation of the seismic isolation layer with a small yielding force (restoring force/gravity less than or equal to 1) increases with the increase of natural period.

Key words：isolated structure; inelastic displacement spectrum; ground motion; field classification

收稿日期：①2015-09-28

基金项目：陕西省工业攻关项目(2013K07-07)；陕西省教育厅专项科研计划项目(2013JK0612)

作者简介：田英侠，女，硕士生导师，副教授，主要研究方向为结构抗震。E-mail:tianyingxiall@qq.com。 通信作者：胡高兴。E-mail:864976195@qq.com。

中图分类号:TU352.1

文献标志码：A

文章编号:1000-0844(2016)03-0353-07

DOI:10.3969/j.issn.1000-0844.2016.03.0353