宁波深厚软土动力特性研究及其地震响应分析①

陈　斌， 张栋梁， 张春进， 杨亚勤， 王国波

(1.宁波市轨道交通集团有限公司，浙江 宁波315012； 2.上海市城市建设设计研究总院，上海 200125；3.武汉理工大学道路桥梁与结构工程湖北省重点实验室，湖北 武汉 430070)

宁波深厚软土动力特性研究及其地震响应分析①

陈斌1， 张栋梁2， 张春进1， 杨亚勤1， 王国波3

(1.宁波市轨道交通集团有限公司，浙江 宁波315012； 2.上海市城市建设设计研究总院，上海 200125；3.武汉理工大学道路桥梁与结构工程湖北省重点实验室，湖北 武汉 430070)

摘要：利用Davidenkov模型对宁波深厚软土地区土动力试验数据进行拟合分析，确定相关拟合参数，结果表明该模型能较好地描述软土的动剪切模量和动阻尼比随动剪应变的变化规律。然后，基于等价线性化方法以及ANSYS软件的APDL语言进行简单的二次开发，编写Davidenkov模型计算程序，并利用经典的SHAKE软件进行验证，结果表明该程序计算结果很好，能解决目前商业软件中缺乏合适的土体非线性动力本构模型的不足。最后，利用开发的模型计算分析宁波深厚软土的地震响应规律，并与规范推荐的简化计算公式进行比较分析，结果表明规范推荐的公式得到的土体响应偏大，对于地下结构的抗震设计偏于保守。研究成果对确定深厚软土地区土体动力特性及其地震响应研究提供了合理的计算方法。

关键词：软土； 动力特性； 地震响应； Davidenkov模型； SHAKE； 等价非线性

0引言

历次大震的震害调查均表明软土会放大地震动效应[1]，因此极有必要加强软土，特别是深厚软土地区结构(包括地下结构和地表结构)的地震响应规律研究[2-3]，而其中最根本的是必须先研究深厚软土自身的动力特性。

目前已有大量关于土动力特性的研究，其中较有代表性的是Hardin和Drnevich在全面分析各参数对土动剪切模量和阻尼比影响的基础上，通过试验得到了土体G/Gmax-γ和λ-γ关系曲线[4-5]，即常见的Hardin-Drnevich模型，这是目前土体等效非线性模型的基础。后来，Seed等[6]发现Davidenkov模型可以更好地描述软土的动剪应力与动剪应变之间的关系。国内学者刘齐建[7]、陈国兴等[8]、周健等[9]以及李晓飞等[10]分别对上海、南京和武汉等地区的软土进行了大量的动力试验研究，均表明Davidenkov模型能较好地描述软土的动力特性。宁波地区属于典型的深厚软土地区，软土层一般厚达90m，最厚达几百米，该模型是否也能够描述宁波深厚软土？这是本文需要解决的第一个问题。本文拟利用宁波深厚软土的土动力试验数据，对其进行拟合分析，由此分析该模型是否适用于宁波深厚软土。

另外，目前常用的商业软件ANSYS、SAP2000、FLAC3D等均没有很好的土体非线性动力本构模型(只有ZSOIL中附带了HHS模型)，因而均未进行非线性地震响应分析。因此，基于上述Davidenkov模型，利用ANSYS软件中的APDL语言进行简单的编程，实现Davidenkov模型的二次开发，并利用经典的SHAKE软件进行验证。

1Davidenkov模型及拟合分析

1.1Davidenkov表达式

相对于传统的Hardin-Drnevich模型，Davidenkov模型采用了较多的拟合参数描述土体动剪切模量和动阻尼比随动剪应变的变化规律，其表达式为：

(1)

(2)

其中:G和Gmax分别为土体瞬时和最大动剪切模量;λ和λmax分别为土体瞬时和最大动阻尼比;A、B、β均为拟合参数，当A=1且B=0.5时，该模型边退化为常见的Hardin-Drnevich模型；γr为参考剪应变。这几个拟合参数均可通过对数据点的拟合分析确定。

1.2数据来源

受浙江省工程地震研究所委托，南京工业大学交通院对宁波轨道交通2号线二期工程土层动剪切模量和阻尼比进行试验研究。试验采用GZZ-1型自振柱仪，根据扭转自由振动(自振柱)原理，用计算机控制试验过程并采集试验数据，该设备具有良好的测试精度。所采取的土样以灰色黏土和粉质黏土为主，辅以少量的灰黄色粉质黏土，土样主要以软塑为主，少量试样为可塑和中密。

宁波轨道交通2号线二期工程场地地震安全性评价报告中提供的土动力试验数据表明，宁波地区软土层较厚，多在70～110m，且以90m左右居多，因此本文将场地土深度取为90m。该厚度范围内的土层包括8类土：填土、淤泥质粉质黏土、粉砂、黏土、粉质黏土、淤泥质土、砂土和粉土。

1.3拟合分析

利用上述公式进行拟合分析，得到上述8种土类的拟合参数(表1)。为节省篇幅，本文仅给出数据点较多的淤泥质粉质黏土、黏土和粉质黏土的拟合结果曲线(图1～3)。

表 1　不同土的拟合参数统计值及其相关系数R2

由表1及图1～3可见：

图1　淤泥质粉质黏土动剪切模量、动阻尼比 与动剪应变关系曲线Fig.1　Relationship curves between dynamic shear modulus,dynamic damping ratio and dynamic shear strain of mucky clay

图2　黏土动剪切模量、动阻尼比与 动剪应变关系曲线Fig.2　Relationship curves between dynamic shear modulus, dynamic damping ratio and dynamic shear strain of clay

(1) 除填土(数据较少)以及砂土之外，其他几种土类的A值均稍大于1.0，B值均在0.5附近，也即表明可以采用经典的Hardin模型描述宁波软土的动力特性；

图3　粉质黏土动剪切模量、动阻尼比与动剪 应变关系曲线Fig.3　Relationship curves between dynamic shear modulus, dynamic damping ratio and dynamic shear strain of silty clay

(2) 各种土类拟合得到的相关系数R2均大于0.98，即拟合结果较好。因此能采用多参数的Davidenkov模型描述宁波深厚软土的动力特性。

2程序编写及验证

等价线性化方法具有概念明确、计算简单等特点，是目前土体地震分析中较为常用的方法，其基本思想是：认为在很短的时间间隔内土体是弹性的，可计算得到土体在该时步内的响应，但到了下一时间步时，土体的模量则衰减了，阻尼增大了，也即以上一时步结束时刻的状态作为该时步的初筛条件，并按指定公式计算衰减后的剪切模量以及增加后的阻尼比进行该时步内的计算分析，依次类推。主要步骤可用图4所示流程图表示。

ANSYS软件是一种大型通用软件，既能用于结构工程的分析，也能用于岩土工程的分析，且较新的版本还提供了对于不同工程材料(如混凝土和土)可设置不同阻尼比的功能，而且相对于FLAC3D软件而言，ANSYS的前后处理界面更为友好，因而目前应用十分广泛。本文则基于ANSYS自带的APDL语言(ANSYSParametricDesignLanguage，即ANSYS参数化设计语言))实现上述迭代过程。

图4　程序流程图Fig.4　Program flow chart

自Seed和Idriss于1970 年首次将等效线性化的概念引入岩土地震工程领域，并于1972 年编制了相应的计算程序SHAKE，现在SHAKE版本已更新至SHAKE2000，是国际主流的土层反应分析等效线性化计算程序[11]。本文采用经典的SHAKE程序验证按照上述流程所编写程序的正确性。

由于SHAKE程序计算时需将土层分成若干个子层，每个子层的厚度不宜过大，一般取1m左右。另外该软件也有一个限制，最多的子层数为50个，也就限制了土层深度最多仅能取50m。而宁波属于深厚软土地区，一般厚达90m，如果取90m深度计算，难以实现。考虑到此处仅是验证编制程序的正确性，因此将土层深度取为50m，土层分布情况如表2所列(计算只取到虚线框显示粉质黏土层)。

利用ANSYS建立自由场土体的平面有限元计算模型，计算范围取50m(深)×100m(宽)，底部固定，两侧采用水平滑移边界，及约束竖向位移，释放两侧边的水平位移。地震波采用宁波人工合成波，将其加速度幅值调整为0.1g(g为重力加速度)。有限元模型和输入地震波时程如图5和图6所示。

采用常用的瑞利阻尼模型，该模型系数和的计算式分别为：

(3)

(4)

式中：ξ为阻尼比，一般按照经验或规范取值；ω1和ω2均为特征频率，邹德高等[12]详细讨论了特征频率的取值，分别取体系基频(0.83Hz)与输入地震波的主频。在早期的ANSYS软件计算分析中，只能设置一个阻尼比常数，而最新的版本中，可针对不同的材料设置不同的阻尼比，因而本文将土体和钢筋混凝土的阻尼比分别设为0.1和0.05。

图5　自由场计算模型Fig.5　Calculation model for free field

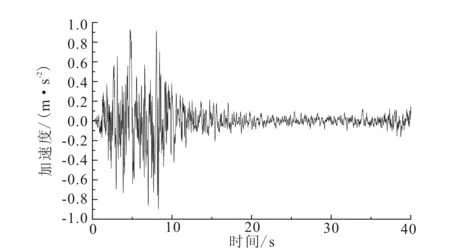
图6　宁波人工地震波加速度时程曲线Fig.6　Acceleration time history curve under the input of Ningbo artificial wave

土层名称厚度/m泊松比弹性模量/MPa密度/(kg·m-3)剪切波速/(m·s-1)填土20.427.361860118淤泥质黏土30.445.211740102淤泥80.457.181690121淤泥质粉质黏土70.4311.261750150含粉砂粉质黏土50.3714.231840168粉质黏土50.3916.851830182黏土40.4220.741790202粉质黏土80.3925.871790228粉质黏土70.3931.701810251粉质黏土40.3946.351890297粉砂夹粉质黏土110.3758.851880338粉砂30.3659.621885341粉质黏土50.3961.061900340黏土80.4268.001900355粉砂10.3699.332100417圆砾110.35143.202200491

分别利用有限元程序及SHAKE91程序计算自由场土体的地震响应，提取土体表面节点的水平加速度时程曲线及其相应的傅氏谱曲线(图7)。由图7可看出两种方法得到的曲线几乎重合，表明本文编制程序的合理性，可用于宁波深厚软土的地震响应分析。

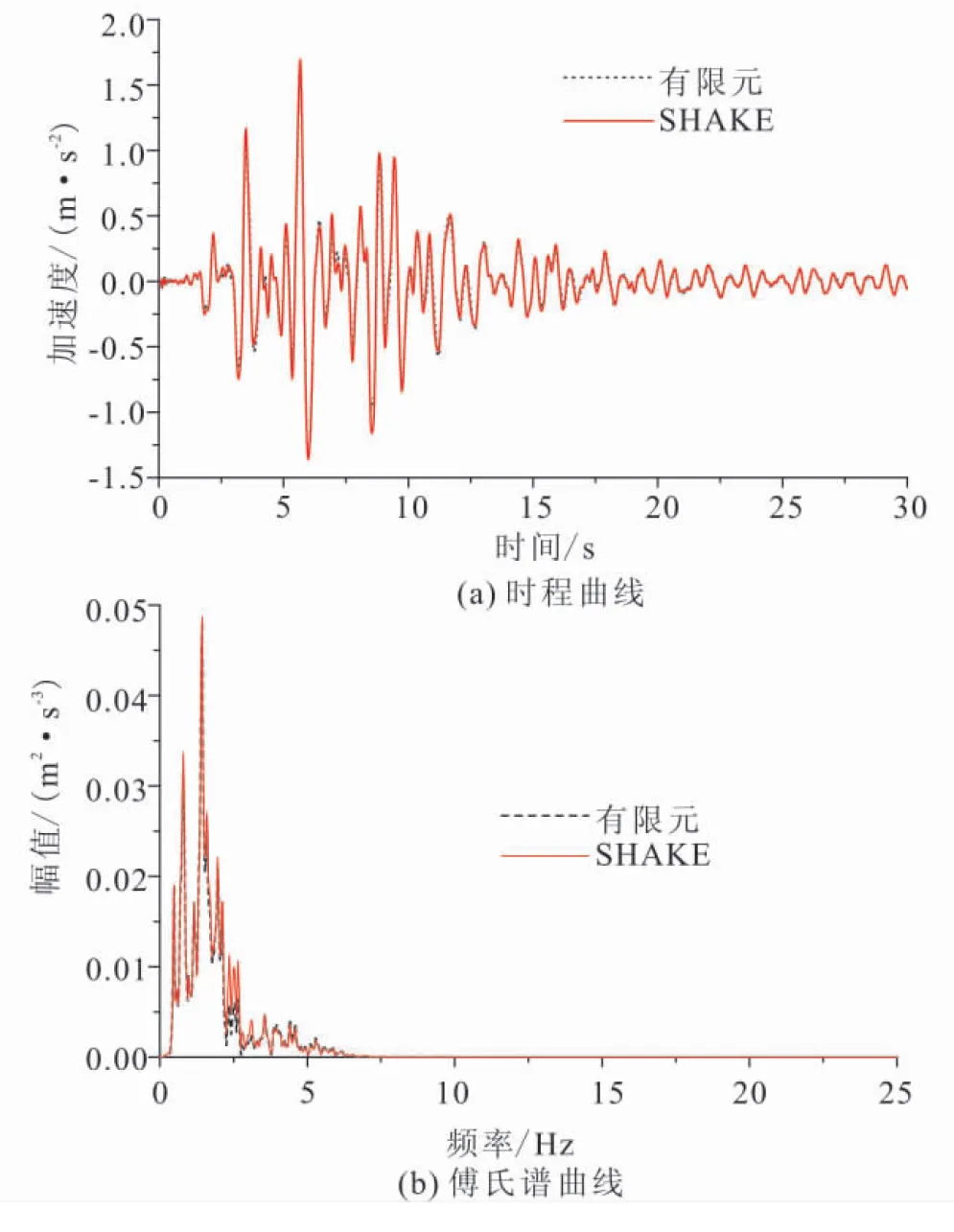
图7　土体表面节点水平加速度时程及其傅氏谱曲线Fig.7　Horizontal acceleration time history and its Fourier spectrum curves of soil surface node

3宁波深厚软土地震响应分析

本小节利用上式验证的自编程序，计算分析真实土层条件下宁波深厚软土的地震响应。土层分布参见表2，总深度92m，计算宽度取200m，边界条件、阻尼设置等与上一节相同，计算模型也可参照图5。地震波仍采用宁波人工波，参照宁波轨道交通的场地安评报告中提供的参数，50年超越概率10%时基岩面输入的宁波人工程合成波加速度峰值为0.077g。图8为地表节点水平加速度时程曲线，其峰值约为1.386m/s2，其与输入加速度峰值0.77m/s2的比值约为1.8，也即场地加速度放大系数为1.8。

图8　土体表面节点水平加速度时程曲线(实际土层)Fig.8　Horizontal acceleration time-history curves of soil surface node (for actual soil layers)

目前我国的《城市轨道交通结构抗震设计规范》(GB50909-2014)推荐反应位移法作为地下结构抗震设计的简化分析分析方法，而反应位移法中一个主要的荷载便是土体变形强加给地下结构的变形，用地震土压力的形式体现。因此土体的位移沿土体深度的响应关系到地下结构地震响应的合理性和精确性。为便于实际工程设计人员使用，《城市轨道交通结构抗震设计规范》(GB50909-2014)中将位移沿深度的变化简化为余弦变化，即：

(5)

其中：z为土体深度；umax是场地地表最大位移，可根据规范中表5.2.4-1取值,本文取0.07m;H为设计地震作用基准面的深度，本文取92m。图9为按照规范推荐的经验公式和由有限元计算得到的土体位移模式的比较。由图9可见采用规范推荐的方法计算得到的土体,其绝对位移和相对位移均显著大于按有限元程序计算的，因而确定的作用于地下结构侧墙的土压力偏大，依据该结果的结构设计是偏于安全的。考虑到SHAKE计算及有限元分析相对较为复杂，不利于实际工程设计人员的使用，因而可参照规范推荐的位移计算简化公式。

图9　不同方法时土体位移模式的比较Fig.9　Comparison of soil displacement mode using different methods

4结语

本文对宁波深厚软土动力特性及其地震响应规律进行了探讨，并取得如下主要结论：

(1) 首先基于宁波深厚软土的土动力试验数据，采用多参数的Davidenkov模型对其进行拟合分析，确定了不同土类的拟合参数，结果表明Davidenkov模型能较好描述宁波深厚软土的动力特性；

(2) 然后采用等效非线性方法，在ANSYS软件平台上利用APDL语言实现了Davidenkov模型的编写，并利用经典的一维土层地震响应分析工具SHAKE对自编程序进行验证，结果表明编写的程序是合理的；

(3) 利用上述程序计算分析宁波深厚软土的放大效应，并对比分析规范推荐的位移模式与有限元计算得到的位移模式的区别，结果表明前者得到的土体位移偏大，使结构设计偏于安全。

参考文献(References)

[1]马险峰.地下结构的震害研究[D].上海：同济大学，2000.

MAXian-feng.StudyonEarthquakeDamageforUndergroundStructure[D].Shanghai:TongjiUniversity,2000.(inChinese)

[2]刘蕊，李延涛，杨德健，等.软土地区地铁车站地震响应分析[J].地震工程学报，2014,36(1)：16-21.

LIURui,LIYan-tao,YANGDe-jian,etal.SeismicResponseofSubwayStationinSoftSoilArea[J].ChinaEarthquakeEngineeringJournal,2014,36(1):16-21.(inChinese)

[3]梁建文，于军港，张季，等.基于黏弹性边界的地下隧道非线性地震响应分析模型[J].地震工程学报，2014,36(3)：434-440.

LIANGJian-wen,YUJun-gang,ZHANGJi,etal.ANonlinearSeismicResponseAnalysisModelforUndergroundTunnelsBasedontheViscous-springBoundary[J].ChinaEarthquakeEngineeringJournal,2014,36(3):434-440.(inChinese)

[4]HardinBO,DrnevichVP.ShearModulusandDampinginSoils:DesignEquationsandCurves[J].JournaloftheSoilMechanicsandFoundationDivision,ASCE，1972，98(7)：667-692.

[5]HardinBO,DrnevichVP.ShearModulusandDampinginSoils:MeasurementandParameterEffects[J].JournaloftheSoilMechanicsandFoundationDivision,ASCE，1972，98(7)：603-624.

[6]SeedHB,IdrissIM.SoilModulusandDampingFactorsforDynamicResponseAnalysis[R].EERC,ReportNO.70-10,U.C.Berkeley,Calif,1970.

[7]刘齐建.软土地铁建筑结构抗震设计计算理论的研究[D].上海：同济大学，2005.

LIUQi-jian.StudyonSeismicDesignandAnalysisTheoryforSubwayStructuresinSoftSoil[D].Shanghai:TongjiUniversity,2005.(inChinese)

[8]陈国兴，庄海洋.基于Davidenkov骨架曲线的土体动力本构关系及其参数研究[J].岩土工程学报，2005,27(8)：860-864.

CHENGuo-xing,ZHUANGHai-yang.DevelopedNonlinearDynamicConstitutiveRelationsofSoilsBasedonDavidenkovSkeletonCurve[J].ChineseJournalofGeotechnicalEngineering,2005,27(8):860-864.(inChinese)

[9]周健，秦天，孔戈.武汉长江隧道横断面地震响应分析[J].工程抗震与加固改造，2007,29(2)：84-92.

ZHOUJian,QINTian,KONGGe.TransverseSeismicResponseStudyofWuhanChangjingTunnel[J].EarthquakeResistantEngineeringandRetrofitting,2007,29(2):84-92.(inChinese)

[10]李晓飞，孙锐，袁晓铭.基于实际记录的现有等效线性化分析程序对比研究[J].地震工程学报，2015,37(1)：144-151.

LIXiao-fei,SUNRui,YUANXiao-ming.ComparativeStudyonExistingEquivalentLinearAnalysisProgramsBasedonKiK-net[J].ChinaEarthquakeEngineeringJournal,2015,37(1):144-151. (inChinese)

[11]李瑞山，袁晓铭，李程程.基于黏弹性解的土层地震反应分析程序LSSRLI-1和SHAKE2000的对比[J].地震工程与工程振动，2015,35(3)：17-27.

LIRui-shan,YUANXiao-ming,LICheng-cheng.Visco-elasticSolutionBasedComparisonbetweentheGroundResponseAnalysisProgramsLSSRLI-1andSHAKE2000[J].EarthquakeEngineeringandEngineeringVibration,2015,35(3):17-27. (inChinese)

[12]邹德高，徐斌，孔宪京.瑞利阻尼系数确定方法对高土石坝地震反应的影响研究[J].岩土力学，2011，32(3)：797-803.

ZOUDe-gao,XUBin,KONGXian-jing.AStudyofInfluenceofDifferentMethodforCalculatingRayleightDampingCoefficientonHighEarth-rockDamSeismicResponse[J].RockandSoilMechanics,2011,32(3):797-803.(inChinese)

AnalysisofDynamicCharacteristicsandSeismicResponseofDeepSoftSoilinNingboArea

CHENBin1,ZHANGDong-liang2,ZHANGChun-jin1,YANGYa-qin1,WANGGuo-bo3

(1.Ningbo Rail Transit Group Co. Ltd., Ningbo 315012, Zhejiang, China;2.Shanghai Urban Construction Design & Research Institute,Shanghai 200125,China;3.Hubei Key Laboratory of Roadway Bridge and Structure Engineering, Wuhan University of Technology, Wuhan 430070, Hubei, China)

Abstract：In this study, we used the Davidenkov model to conduct a fitting analysis on dynamic test data of deep soft soil in the city of Ningbo and then determined the relevant fitting parameters. The fitting results demonstrate that the Davidenkov model can describe the dynamic characteristics of the Ningbo deep soft soil well. We wrote the computation program for Davidenkov model in APDL language using ANSYS software based on the equivalent nonlinear method and verified its correction by the classic earthquake response program SHAKE. The results show that the program is effective and can address the lack of nonlinear constitutive soil models in existing commercial software. We used the above program to compare relevant codes and analyzed the seismic responses of the Ningbo deep soft soil. The analysis results indicate that the soil displacement obtained by the formula recommended by the code is actually greater than expected, which means that the underground structure that was designed according to code is conservative. The research results from this study provide a reasonable method for calculating soil dynamic characteristics and conducting seismic response analysis of deep soft-soil areas.

Key words：soft soil; dynamic characteristics; seismic response; Davidenkov model; SHAKE; equivalent nonlinear

收稿日期：①2014-08-20

基金项目：武汉市城乡建设委员会科研项目(201417)

作者简介：陈斌(1964-)，男，四川安岳人，博士后，教授级高工，主要从事城市轨道交通研究与管理工作。E-mail:Chenbin.nb@163.com。 通信作者：王国波(1979-)，男，湖北孝昌人，博士，副研究员，主要从事工程结构的抗震分析。E-mail:wgb16790604@126.com。

中图分类号:TU435

文献标志码：A

文章编号:1000-0844(2016)03-0338-06

DOI:10.3969/j.issn.1000-0844.2016.03.0338