基于α-β-γ滤波的迫击炮定位
基于α-β-γ滤波的迫击炮定位
张强**
(中国西南电子技术研究所,成都 610036)
摘要:针对迫击炮的侦察定位问题,介绍了一种基于α-β-γ滤波的定位方法。该方法首先根据外弹道学确定弹丸飞行的质心运动方程,然后利用常增益的α-β-γ滤波跟踪求解弹丸的运动参数,最后通过龙格-库塔(Runge-Kutta)方法求解质心运动方程,并外推求得炮位位置。仿真结果表明,该方法在保证较高迫击炮定位精度的同时实时性能较传统方法大幅提升,有显著的工程意义。
关键词:迫击炮定位;质心运动方程;α-β-γ滤波;龙格-库塔方法
1引言
迫击炮具有构造简单、操作灵活、造价低廉、弹道弯曲、最小射程近、射速快、可实时伴随步兵作战等优点,对开阔地及掩体内目标、各种野战工事甚至高大障碍物(如山坡)背后目标都有着良好的毁伤破坏作用,作为步兵近距离火力支援的有效武器,现今仍被各国军队大量装备[1-3]。为了提高我方炮兵的作战反应速度和火炮命中概率,各国都在不断加强火炮侦察定位雷达的研究,以实现对敌方炮火的有效压制,典型的炮位侦察雷达有美国AN/TPQ-36 、AN/TPQ-37“火力发现者”[1,4]和轻型反迫击炮雷达(LCMR)。火炮定位算法作为炮位侦察定位雷达的关键技术也日益得到重视。文献[5-6]所提出的外弹道仿真方法未通过滤波跟踪算法对弹丸的运动参数进行解算,因此反推炮位的起点易受随机噪声影响,反推炮位的误差较大。文献[7]引入粒子滤波的方法来辨识弹道参数和弹丸的运动参数,然后再外推敌方炮位,该方法定位精度高,但是算法复杂、实时性差,不能满足工程应用的需要。实践表明,卡尔曼滤波[8]虽然复杂程度不及文献[7]中的粒子滤波方法,但是它的运算时间也比较长,实时性仍然不够好。因此,有必要寻求一种在保证一定滤波精度条件下(即工程上允许的近似)运算量小、速度快的滤波器。理论研究表明,在一定的限定条件下,α-β-γ滤波器与卡尔曼滤波器具有相一致的最佳增益[9],但是运算量却大大减小。本文研究α-β-γ 滤波在迫击炮定位中的应用。
2迫击炮弹丸运动数学模型
迫击炮弹丸的运动弹道是一种类抛物线,但是由于受到空气阻力等因素影响,实际弹道与抛物线又有较大的差异,特别是对低射角的飞行弹道而言,若用抛物线方程来逼近,产生的定位误差将不可接受,甚至可能是发散的,无法外推,因此,本文采用弹丸的质心运动方程来描述其飞行轨迹[6]。
迫击炮弹飞行轨迹示意图如图1所示,弹丸的飞行轨迹位于XYZ三维笛卡尔坐标系内,炮位位于H点,炮位侦察雷达位于X轴方向。

图1 迫击炮弹飞行轨迹示意图
那么以时间t为自变量,在三维直角坐标系中弹丸质心运动方程可描述为
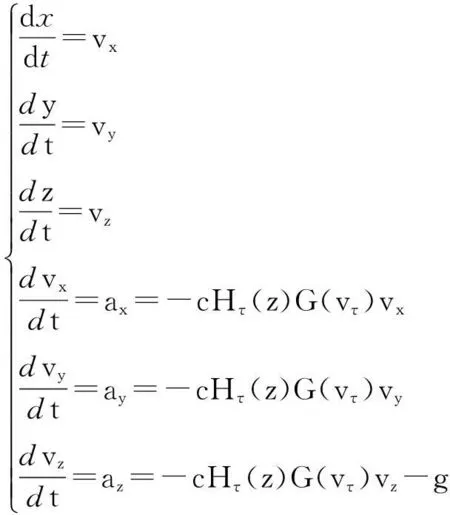
(1)
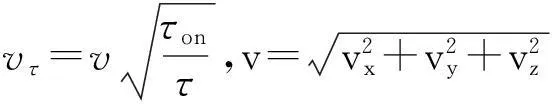
弹丸的质心运动方程是一种理想情况,它把弹丸看作质点,在空中飞行时只受到重力和空气阻力的影响,且不考虑马格洛斯力、升力和科氏力等,它是一种气动参数少但能较准确反映飞行弹丸运动规律的弹道方程。弹丸质心运动方程虽然在全弹道上与真实弹道有一定差距,但是完全能够满足炮位侦察的要求。
3α-β-γ滤波解算目标运动参数
为了获得准确的弹丸运动参数,有必要通过滤波跟踪对雷达量测数据进行平滑,并获得后续炮位反推的起点。典型的滤波跟踪方法就是卡尔曼滤波,但是卡尔曼滤波的增益计算过程较为复杂,需要耗费大量时间,影响算法的实时性。α-β-γ滤波作为卡尔曼滤波的特殊形式,由于它是一种常增益滤波器,计算复杂度极大地下降,但是针对匀加速运动模型的目标却和传统卡尔曼滤波有相一致的最佳增益[9]。而迫击炮弹丸由于仅受到万有引力和空气阻力作用可以被认为处于匀加速运动状态,所以引入α-β-γ滤波器来对雷达量测数据进行平滑并解算目标的运动参数。对于笛卡尔坐标系下九维向量的α-β-γ平滑滤波可描述如下。
弹丸运动的状态方程可描述为
X(k+1)=F(k)X(k)+Γ(k)v(k),k=0,1,2,…,99。
(2)
式中,状态向量为X(k)=[x vxaxy vyayz vzaz]′;状态转移矩阵
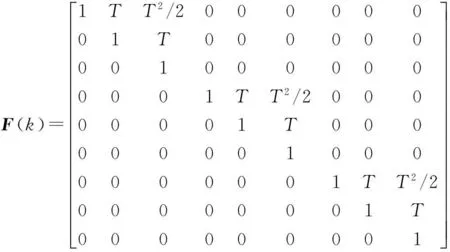
过程噪声分布矩阵
Γ(k)=[T2/2 T 1 T2/2 T 1 T2/2 T 1]′;v(k)为过程噪声,是零均值高斯白噪声。
弹丸的量测方程为
Z(k)=H(k)X(k)+W(k)。
(3)
式中,量测矩阵

W(k)为量测噪声,是零均值的白噪声,与过程噪声序列相互独立。
状态一步预测为

(4)
常增益的表达式为
K(k+1)=
[αβ/Tγ/T2αβ/Tγ/T2αβ/Tγ/T2]。
(5)
公式(5)中的常增益是机动指标的函数,工程上常用与采样时刻k有关的方法来确定α、β和γ的值,如公式(6)~(8)所示:
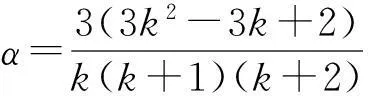
(6)
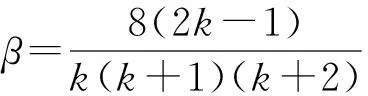
(7)

(8)
对α来说,从k=1开始取值;对β来说,从k=2开始取值;对γ来说,从k=3开始取值。α、β、γ值与k的关系如表1所示。

表1 α、β、γ值与k的关系
最后可得α-β-γ滤波的状态更新方程为
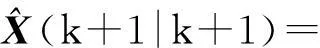
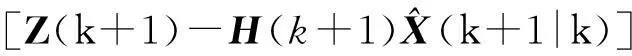
(9)
由于基于α-β-γ滤波的目标解算方法在计算增益时不需要计算新息协方差和更新协方差向量等过程,计算复杂度大大降低。
4龙格-库塔法炮位反演
弹丸的质心运动方程(1)是一个微分方程,可用龙格-库塔(Runge-Kutta)方法来实现微分方程的解[6-7]。
对于微分方程如公式(10),那么用四阶龙格-库塔方法的求解如公式(11)所示:
x′=f(t,x),x(t0)=x0;
(10)
xi+1=xi+hφ(ti,xi,h),i=0,1,…。
(11)
对于用龙格-库塔方法进行微分方程数值求解而言,若x(t+h)-[x(t)+hφ(t,x(t),h)]=O(hp+1),则称以上迭代公式为p阶公式,p的大小反映了截断误差的高低,越高阶精度越高。本文所用的四阶龙格-库塔方法其p=4,精度较高。
龙格-库塔炮位反推的起点为α-β-γ滤波获得的精度较高的处于下降段的弹丸轨迹点,选取恰当的时间间隔h即可获得较高的炮位反演精度,当炮位迭代反推至z=z0时的弹丸坐标(x0,y0)即为迫击炮位置所在,其中z0为弹丸飞行曲线与地形坐标交点的高度值。
5算法流程
基于α-β-γ滤波的迫击炮定位方法的详细算法流程图如图2所示。

图2 定位算法流程图
5.1弹道参数的初始化
质心运动方程主要弹道参数根据《弹箭外弹道学》[10]确定:
(1)弹道系数c=0.8613;
(2)地面标准虚温值τon=15℃,z高度处的虚温值τ=τon-0.006328z;
(3)空气密度函数
H(z)=(1-2.1904×10-5z)4.399;
(4)空气阻力函数
式中,v的单位为m/s;
(5)重力加速度g=9.8 m/s2。
5.2量测值的初始化
对于侦察定位雷达每次给出的目标测量值为斜距、方位角和俯仰角,即(R,α,β)。为了方便算法实现,将其转换到雷达笛卡尔坐标系下为Z=(x,y,z),那么系统的初始状态向量可利用前三个时刻的雷达测量值Z(0)、Z(1)和Z(2)确定,即
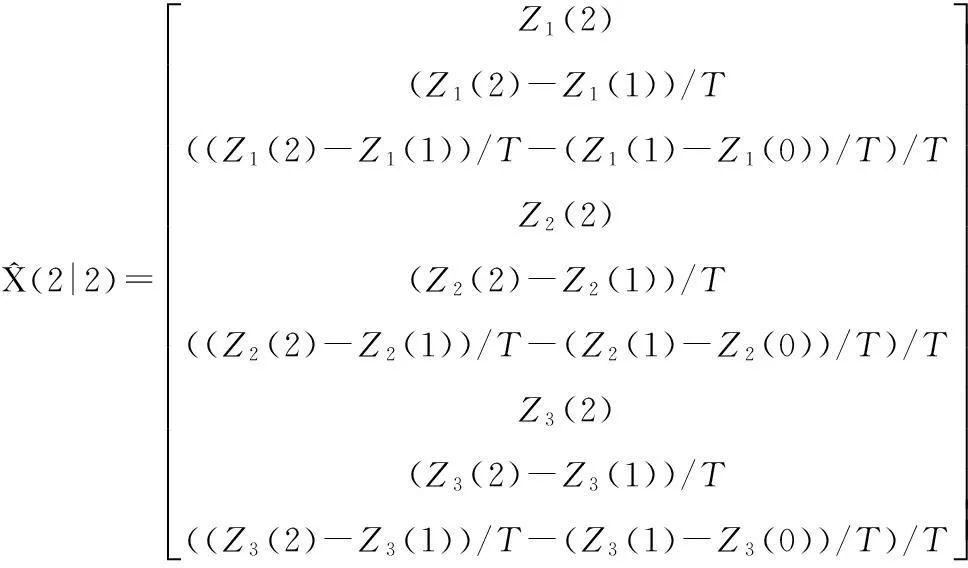
5.3滤波平滑
侦察雷达需要给出13个测量值,其中时间间隔为T=0.1s,系统根据第3节介绍的常增益α-β-γ滤波从k=3时开始滤波平滑,最终获得k=12的弹丸运动参数(x1vx1ax1y1vy1ay1z1vz1az1),即炮位反推的起点。
5.4炮位反推
选取时间间隔h=0.1s,根据第4节介绍的龙格-库塔方法进行炮位反推,当炮位迭代反推至z=z0时的弹丸坐标(x0,y0)即为迫击炮位置所在,其中z0为弹丸飞行曲线与地形坐标交点的高度值。
6仿真与分析
以美国某型81mm口径的迫击炮为例,用Matlab进行仿真实验。设定弹丸在YOZ平面内飞行,地形与水平面相同,那么可从网络查阅获得该型迫击炮在发射角为45°和60°时的相关运动参数,如表2所示。

表2 迫击炮相关参数
仿真实验中首先根据表2中迫击炮相关参数得到弹丸飞行路径图,然后取飞行路径下降段的连续13点采样值作为雷达的量测值,并据此进行α-β-γ滤波和炮位反推,同时将本文方法与基于卡尔曼滤波[8]和粒子滤波[7]的方法进行比较,反推的炮位坐标与真实坐标如表3所示, 可见虽然本文炮位反演方法的绝对误差分别为36 m和29 m,高于其他两种方法,但是仍具有很高的炮位反推精度,对实际工程应用而言迫击炮定位精度小于50 m就是非常有意义的。

表3 定位精度比较
本文算法与基于卡尔曼滤波和粒子滤波的炮位反演算法计算时间比较如表4所示,表中以本文方法在45°发射角的反推时间为单位1,其余时间为单位1的倍数,可见本文方法在计算时间上优势明显。

表4 计算时间比较
仿真分析中的弹道参数设置是具有通用性的,只是未充分考虑弹丸目标的起伏特性和雷达测量噪声对定位结果的影响,在实际工程中定位精度还有降低的可能,但该方法亦不失为一种性能较好的迫击炮定位方法。
7结束语
本文介绍了一种基于α-β-γ滤波的迫击炮侦察定位方法。该方法利用α-β-γ滤波跟踪获得迫击炮弹丸飞行的相关参数,然后用四阶龙格-库塔方法来解算弹丸的轨迹运动方程,实现对炮位的准确外推。仿真结果表明,该方法虽然侦察定位精度略微有所下降,但是实时性能相对文献[7-8]的方法有极大提升,有显著的工程应用价值。在后续的工作中有必要进一步研究该方法推广到其他舰炮、坦克炮等火炮的定位效果。
参考文献:
[1]朱元亮.国柱阵炮位侦察雷达关键技术的研究[D]. 西安:西安电子科技大学,2010:2-15.
ZHU Yuangliang. Study on the key techniques of artillery location radar with the cylindrical array antenna[D]. Xi′an:Xidian University,2010:2-15.(in Chinese)
[2]郭蔚.炮位侦校雷达信号处理关键技术研究[D]. 南京:南京理工大学,2013.
GUO Wei. Key technology of Artillery locating radar signal processing[D]. Nanjing :Nanjing University of Science and Technology,2013.(in Chinese)
[3]杨翔,王雨时,闻泉.迫击炮弹空气动力特性攻角系数数值研究[J].弹箭与制导学报,2014,34(2):139-142.
YANG Xiang,WANG Yushi,WEN Quan. Numerical simulation on aerodynamic characteristics about angle of attack coefficient of mortar projectiles[J]. Journal of Projectiles,Rockets,Missiles and Cuidance,2014,34(2):139-142.(in Chinese)
[4]王东,张鹏,梁开莉.武器定位雷达侦察模式下多目标能力研究[J].现代雷达,2011,33(11): 6-10.
WANG Dong,ZHANG Peng,LIANG Kaili. A study on multiple-target locating capability of weapon locating radar in reconnaissance mode[J]. Modern Radar,2011,33(11): 6-10.(in Chinese)
[5]杨献辉,赵俊利.基于MATLAB的迫击炮外弹道模型仿真研究[J].装备制造技术,2011(2):24-26.
YANG Xianhui,ZHAO Junli. A simulation research on the external trajectory of mortars based on MATLAB[J]. Equipment Manufacturing Technology,2011(2):24-26.(in Chinese)
[6]伍建辉,董亮.基于Matlab迫击炮外弹道仿真[J].火控雷达技术,2014,43(2):39-42.
WU Jianhui,DONG Liang. Simulation on external trajectory of mortar based on matlab[J]. Fire Control Radar Technology,2014,43(2):39-42.(in Chinese)
[7]胡献君,王航宇,周德超.粒子滤波跟踪弹道下降段在炮位侦察中的应用[J].现代防御技术,2013,41(1):104-19.
HU Xianjun,WANG Hangyu,ZHOU Dechao. Application of tracking descend trajectory with particle filter on detecting cannon location[J]. Modern Defence Technology,2013,41(1):104-19.(in Chinese)
[8]唐吉祥,沈云山. 卡尔曼滤波在炮位侦察雷达中的应用[J].电光与控制,2004,11(1):48-51.
TANG Jixiang,SHEN Yunshan.Application of Kalman filter in cannon locating radar[J].Electronics optics & Control,2004,11(1):48-51.(in Chinese)
[9]何友,修建娟,张晶炜,等.雷达数据处理及应用[M].北京:电子工业出版社,2012:15-50.
HE You,XIU Jianjuan,ZHANG Jingwei,et al. Radar Data Processing with Applications[M]. Beijing: Publishing House of Electronics Industry,2012:15-50.(in Chinese)
[10]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008.
HAN Zipeng. Exterior Ballistics of Projectiles and Rockets[M]. Beijing:Beijing Institute of Technology Press,2008.(in Chinese)

张强(1986—),男,四川邻水人,2012年于中国科学院获博士学位,现为工程师,主要研究方向为图像处理、目标识别和雷达系统设计。
ZHANG Qiang was born in Linshui,Sichuan Province,in 1986. He received the Ph.D. degree from Chinese Academy of Sciences in 2012. He is now an engineer. His research interests include image processing,target recognition,radar system design.
Email: zhangqiang_ioe@126.com
引用格式:张强.基于α-β-γ滤波的迫击炮定位[J].电讯技术,2015,55(6):634-638.[ZHANG Qiang.Trench Mortar Locating Based on α-β-γ Filter[J].Telecommunication Engineering,2015,55(6):634-638.]
Trench Mortar Locating Based on α-β-γ Filter
ZHANG Qiang
(Southwest China Institute of Electronic Technology,Chengdu 610036,China)
Abstract:For the locating problem of trench mortar,a locating method based on α-β-γ filter is presented. First,centroid moving equations are determined according to the exterior ballistics. Then the motion parameters are solved by the α-β-γ tracking filter with constant gain. Finally, the trench mortar position is deduced by solving the centroid moving equations with the Runge-Kutta method. The simulation results show that the proposed method has good locating precision with much shorter time compared with conventional method,and it is valuable for engineering.
Key words:trench mortar locating;centroid moving equation;α-β-γ filter;Runge-Kutta method
作者简介:
中图分类号:TN97
文献标志码:A
文章编号:1001-893X(2015)06-0634-05
通讯作者:*zhangqiangioe@126.comCorresponding author:zhangqiangioe@126.com
收稿日期:*2014-09-28;修回日期:2015-04-17Received date:2014-09-28;Revised date:2015-04-17
doi:10.3969/j.issn.1001-893x.2015.06.009

