四阶龙格-库塔方法的程序设计与应用

罗丽珍 吴庆军

摘 要 本文通过介绍四阶龙格-库塔方法，通过预报斜率和泰勒展开式推导出龙格—库塔格式。了解它的基本思想与算法步骤、MATLAB语言编写的程序。列举一些例子，运用四阶龙格-库塔方法的MATLAB程序在软件中运行，求解出常微分方程的数值解，同时将求解出的数值解与精确解进行比较。

关键词 龙格-库塔方法 常微分方程 数值解

中图分类号：TP337文献标识码：A

0引言

从17世纪以来国内外数学家对常微分方程的研究取得了很多的成果.欧拉在研究中指出常微分方程存在唯一解和无数解，他用近似值求解微分方程，发现用积分因子求解微积分方程的特殊算法。拉格朗日建立了一阶微分方程理论，他将参数变法应用到四阶非齐次方程的求解。

我们生活中许多问题的解决都运用到常微分方程，常微分方程的数值解法中经常使用的方法是四阶龙格-库塔方法。各个领域和工程问题中的原理和演变规律都是用常微分方程来描述的，如在物理方面的电路中电流变化的规律、航天航空方面卫星运转问题、经济方面物品供给以及需求与物价的之间的关系、军事方面研究深水炸弹在水下的运动等。对这些事物、现象变化规律的描述、认知和分析，需要运用常微分方程来解决。人们使用常微分方程数值解法的四阶龙格-库塔方法去研究这些问题很实用，而且具有很重要的应用价值。

目前，常微分方程在解决我们生活中的问题很实用，许多问题都运用常微分方程来求解。中国科学技术大学学者倪兴在常微分方程的研究中写了关于欧拉法、方法等几种方法，他运用常微分计算卫星运动的初轨，把方法运用到卫星轨道改进的例子中;扬州大学学者冯建强和孙诗一研究四阶方法的推导，他写出了如何推导的过程。在高校数值分析、数值计算方法与实验等教材中，许多作者都出版关于常微分方程初值问题数值解法的教材书，欧拉方法、改进欧拉法和方法等，同时在教材书中写入各种实际问题的例子，运用这些方法去解决常微分方程的初值问题。本文主要介绍常微分方程数值解法的四阶方法，使用四阶方法求解常微分方程。介绍四阶方法的基本思想、算法步骤和MATLAB程序，同时使用四阶方法在案例中解决问题。

1四阶方法

1.1四阶方法的思想与算法

对于一阶常微分方程初值问题，根据拉格朗日微分中值定理可知存在使

记为在区间上的平均斜率。

在给定的区间里预测个点处的斜率，再把它们的加权平均作为平均斜率的近似值。这里取在区间上若干个点的斜率值或者预报斜率值的加权平均值，作为平均斜率的近似值，令区间上若干个点的斜率值或预报斜率值为，以及权系数为，使差分格式

当上式为阶时，把它叫做阶龙格—库塔格式.通过上式能够推导得精确度比较高的公式来求解常微分方程。

当时，龙格-库塔的格式为

在上式中，在点的斜率是在点的预报斜率为是，参数都是待定参数。当待定参数使上式是二阶格式时，称上式是二阶龙格-库塔格式。

函数在点的泰勒展开式为

令是准确的，有，根据二元函数泰勒展开有

要使上面的截距误差为，把与泰勒展开式比较可得。通过以上的推导可以得出待定参数的值。

由可知二阶龙格-库塔格式是一个系列的差分格式。当取时得

这是改进的欧拉公式。取，可得

其中

这是常用的二阶龙格-库塔方法，称其为中心格式。

三阶龙格-库塔格式：

三阶龙格-库塔格式是比二阶格式高一阶的格式，它是在二阶龙格-库塔格式的基础上进一步构造得到的格式。当时，龙格-库塔的格式如下

在上式里，在点的斜率是在点和点的预报斜率分别是、，当待定参数和使上式为三阶格式时，则称其为三阶龙格—库塔格式。

类似二阶龙格-库塔格式的推导，得到三阶龙格-库塔格式为：

称其为三阶龙格-库塔格式。

四阶龙格-库塔格式：

同样是根据上述的推导，得到四阶龙格-库塔格式为：

称上式为四阶龙格-库塔格式。在解决许多问题中常常使用的龙格-库塔格式是四阶龙格-库塔格式。

四阶龙格-库塔方法的算法步骤如下：

第一步输入区间等分数，初值;

第二步输出在的个点处的近似值;

第三步令;

第四步计算

令，输出;

第五步如果，令，转向第四步;否则停机。

1.2四階方法的MATLAB程序

四阶龙格-库塔法MATLAB函数文件nark4.m如下：

function [x，y]=nark4（dyfun，xspan，y0，h）

x=xspan（1）：h：xspan（2）;

y（1）=y0;

for n=1：length（x）-1

k1=dyfun（x（n），y（n））;

K2=dyfun（x（n）+h/2，y（n）+h/2*k1）;

K3=dyfun（x（n）+h/2，y（n）+h/2*k2）;

k4=dyfun（x（n+1），y（n）+h*k3）;

y（n+1）=y（n）+h*（k1+2*k2+2*k3+k4）/6

end

x=x';y=y';

1.3四阶方法的应用

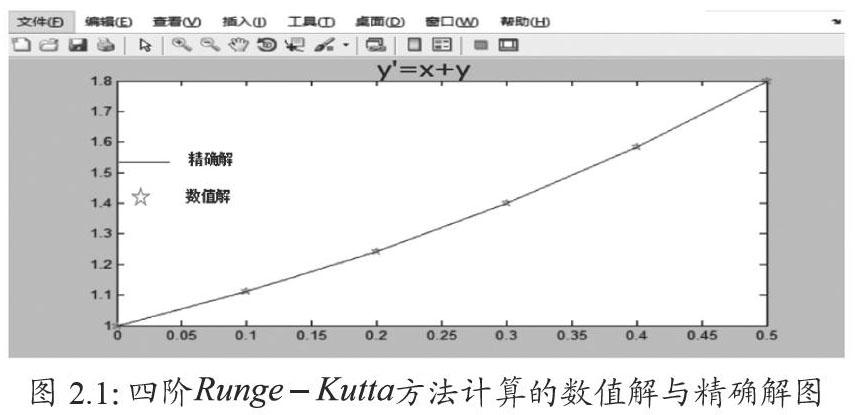
例2.1：用四阶方法求解初值问题的数值解，取步长。其精确解为，并将解得的数值解与精确解进行比较。