电机参数估算与最大转矩电流比控制的研究
朱广,王文白,杜明星,魏克新(天津理工大学天津市复杂系统控制理论及应用重点实验室,天津300384)
电机参数估算与最大转矩电流比控制的研究
朱广,王文白,杜明星,魏克新
(天津理工大学天津市复杂系统控制理论及应用重点实验室,天津300384)
摘要:基于空间矢量控制原理,通过在不同的交直轴电流分配策略下控制永磁同步电机,利用实验数据估算电机参数,并根据估算参数实现了电机的最大转矩电流比控制。实验过程与相应的仿真结果表明,该方法估算的电机参数可用于电机最大转矩电流比控制,能得到较好的控制效果,具有一定的工程实际意义。
关键词:永磁同步电机;参数估算;最大转矩电流比;空间矢量控制
20世纪80年代以后,电机调速技术不断发展,高性能永磁同步电机调速系统的出现引起人们的高度重视,其研究工作主要是针对永磁同步电机的自身性能和对永磁同步电机调速系统的控制效果[1]。在研究和应用过程中,不可避免地需要获得电机的参数,如电机电枢绕组电阻、直轴和交轴电感、主极磁通、电机转动惯量等[2]。但对于永磁同步电机而言,由于永磁体对测量过程的影响,部分电机参数的获取方法比较复杂。因此,本文根据工程实践经验,基于转子磁场定向控制原理,介绍一种基于实验的永磁同步电机参数估算方法,并根据估算得到的参数实现了电机在最大转矩电流比控制方式下的稳定运行,验证了该方法的有效性,并对最大转矩电流比控制方式进行研究。与id=0控制方式进行对比,阐述其优缺点。
1 永磁同步电机数学模型与控制方法
1.1电机数学模型
永磁同步电机主要由定子和转子两部分构成。转子通常配备高性能永磁的表面或内部铁磁材料,三相定子绕组通入三相交流电产生旋转磁场。为了方便分析,电机进行以下假设:定子绕组三相对称,气隙均匀,忽略磁饱和效应和铁损耗、忽略高谐波、忽略转子轴摩擦。
永磁同步电机输出的电磁转矩表达式为

式中:pn为极对数;Te为电机电磁转矩;Ψf为转子磁极磁通链;id,iq分别为d轴和q轴电流;Ld,Lq分别为d轴和q轴的电枢电感。
由式(1)可以看出,永磁同步电机输出的电磁转矩由2部分组成:第1部分为永磁转矩,它由交轴电枢反应产生;第2部分为凸极结构产生的磁阻转矩。
1.2控制方法
1.2.1id=0控制
id=0控制是一种比较简单的控制方法,通过设计负反馈调节器近似满足id=0,则此时电磁转矩表达式就转化为

式中:Ψf为常数。
因此电磁转矩Te将与交轴电流iq成正比。可见,若已知一系列电磁转矩Te及对应的交轴电流iq,就可以求得Ψf。但由于含有(Ld-Lq)的项被iq=0消去,因此这里无法求得(Ld-Lq)。
1.2.2最大转矩电流比控制

可见,为实现式(3)、式(4)需要已知Ψf和(Ld-Lq)。其中Ψf可根据1.2.1节中提到的通过id=0控制下的电机控制实验数据求出。而当id≠0时,理论上即可根据一系列电磁转矩Te及对应的交直轴电流id,iq求出(Ld-Lq)。
2 电机参数估算与最大转矩电流比控制的仿真过程
2.1电机Ψf,(Ld-Lq)的求取
图1为Matlab中搭建的永磁同步电机控制系统仿真框图,其中电机参数设定为Ψf= 0.08 Wb,Ld=0.5 mH,Lq=1.5 mH。实际过程中,这些参数均为未知,需要根据实验数据估算出。图1中方框表示电流控制方法,这里首先采用id=0控制,通过调节PI参数使得系统能够稳定运行。根据1.1节的内容,通过给电机施加不同的负载转矩,当系统达到稳态时,记录多组对应的电磁转矩Te与iq,如表1第2列所示。根据式2可估算出Ψf=0.078 Wb。
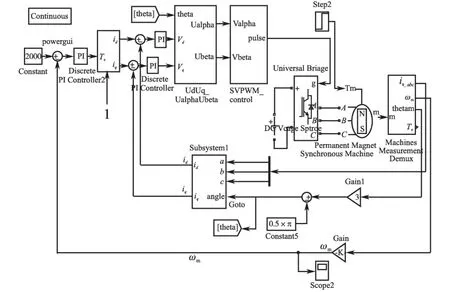
图1 控制系统仿真模型Fig.1 The simulation model of control system
为了估算(Ld-Lq),需要制定一种id,iq的分配策略,满足以下条件:Te>0时,id≠0,否则含有(Ld-Lq)的项将被消去;(Ld-Lq)id与Ψf的数量级要接近,否则含有(Ld-Lq)的项绝对值较小,估算误差较大;id需随iq绝对值的增大而向负方向增大,否则id的变化趋势难以保持一致,给估算带来困难。根据工程经验可以使id=-0.5|iq|,依此修改图1中的电流控制方法,并沿用估算Ψf时的PI调节器参数。通过给电机加载不同的负载转矩,当系统达到稳态时,记录多组电磁转矩Te与对应的id,iq,如表1第3,4列所示。根据式(1)可估算出(Ld-Lq)=-1.1 mH。

表1 两种策略Te变化对应id,iq的稳态值Tab.1 The steady value of id,iqwhen Techanges in both policy
2.2电机控制的实现
为实现最大转矩电流比控制,需要在控制器中实现根据Te计算id,iq的数学关系式,这些关系式可以通过式(3)和式(4)得出,但这将涉及高次方程的求解,其计算量对于微处理器较大,因此需要寻找一种适合工程应用的简化算法来得到id,iq与Te之间的数学关系。
将2.1节求出的电机参数Ψf=0.078 Wb,(Ld-Lq)=-1.1 mH,代入1.2节中式(4),通过Matlab可以得到最大转矩电流比控制方式下,电机可输出电磁转矩范围内,Te与id,iq关系式的曲线,如图2所示。图2中一并给出了Ψf=0.08 Wb,Ld=0.5 mH,Lq=1.5 mH。代入1.2节中式(4)得到的Te与id,iq的关系式的曲线。可以看出,虽然计算求出的电机参数与设定值有偏差,但基于2组参数求得的id,iq与Te的关系曲线非常接近。这说明根据实验数据估算出的电机参数求得的最大转矩电流比控制方式下id,iq与Te之间的数学关系是可用的。
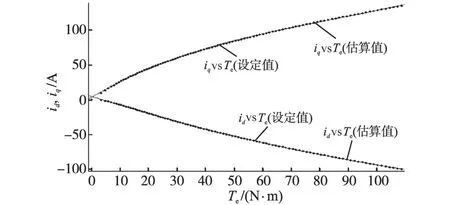
图2 id,iq与Te关系曲线Fig.2 The curves of id,iqand Te
为了得到id,iq与Te的关系,采用曲线拟合工具箱Cftool,在Matlab上对曲线进行多项式拟合。二阶拟合得到的关系式如下式所示:

三阶拟合得到的关系如下式所示:
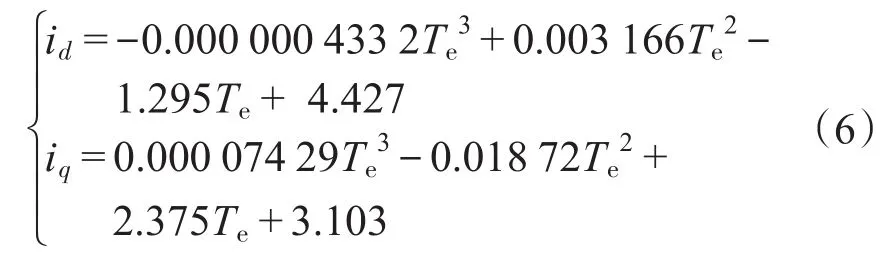
综合考虑拟合精度、微处理器计算速度、模拟量采样周期和传感器精度等限制条件后采用二阶拟合。
将图1中的电流控制方法修改为最大转矩电流比控制。电机转速给定为2 000 r/min,在t= 0.1 s时施加40 N·m负载转矩。当系统再次达到稳态时,id=0和最大转矩电流比控制下,定子三相电流分别如图3、图4所示。

图3 id=0控制三相电流波形Fig.3 Three-phase current waveforms of id=0
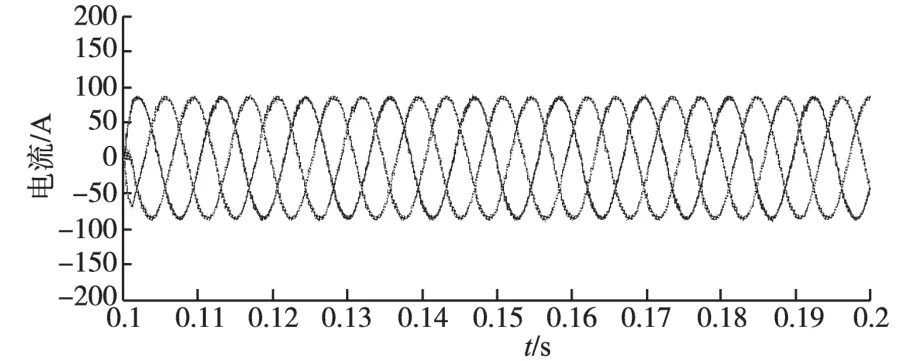
图4 最大转矩电流比控制三相电流波形Fig.4 Three-phase current waveforms of maximum ratio of torque to current
由图3、图4可知,系统稳定时最大转矩电流比控制策略下的定子三相电流明显小于id=0控制策略下的定子三相电流。
3 电机参数估算与最大转矩电流比控制的实验过程
为了验证仿真的正确性,通过实验对其进行进一步验证,硬件操作框图如图5所示,采用C语言编写软件程序,实验参数与仿真参数一致,实现对电机的控制。

图5 硬件试验框图Fig.5 Hardware test diagram
对2.1节的仿真进行实验验证。电机控制器采用id=0控制方式,空载状态下给定电机转速为2 000 r/min,运行至稳态时通过测功机施加负载转矩。当系统再次达到稳态时,记录多组对应的电磁转矩Te与iq,如表2第2列所示。根据式(2)可估算出Ψf=0.078 Wb。
电机控制器改为采用id=-0.5|iq|控制方式,电机运行至稳态时通过测功机施加负载转矩。当系统再次达到稳态时,记录多组对应电磁转矩Te与id,iq,如表2第3,4列所示,根据式(1)可以估算出(Ld-Lq)=-1.1 mH。

表2 两种策略Te变化对应id,iq的稳态值Tab.2 The steady value of id,iqwhen Techanges in both policy
对2.2节的仿真进行实验验证。电机控制器分别采用id=0和最大转矩电流比控制,空载状态下给定电机转速为2 000 r/min,系统达到稳态后通过测功机施加40 N·m负载转矩。当系统再次达到稳态时,id=0和最大转矩电流比控制下,定子三相电流分别如图6、图7所示。

图6 id=0控制三相电流实验波形Fig.6 Three-phase current experimental waveforms of id=0

图7 最大转矩电流比控制三相电流实验波形Fig.7 Three-phase current experimental waveforms of maximum ratio of torque to current
从图6、图7可以看出,转矩40 N·m时,id=0控制时三相电流幅值为115 A,最大转矩电流比控制时电流幅值为104 A,可见同一转矩下最大转矩电流比控制比id=0,控制电流小了9.5%。说明最大转矩电流比控制策略效果明显优于id=0控制策略。
4 结论
本文在空间矢量控制的基础上,对一台未知参数的永磁同步电机进行了参数估算,并根据估算参数实现了最大转矩电流比控制,完成了从仿真到实验验证的全过程。并对最大转矩电流比控制与id=0控制效果进行了比较。通过仿真与实验对比,结果表明,电机可以平稳运行于最大转矩电流比控制策略下,验证了所测电机参数的可用性,验证了电磁转矩与交直轴电流的数学关系可通过二阶多项式拟合近似实现,验证了最大转矩电流比控制相比于id=0控制需要更小的定子电流就能够输出目标转矩。因此,本文介绍的永磁同步电机参数估算方法与应用到最大转矩电流比控制的方式是有效的。
参考文献
[1]陈荣.永磁同步电机控制系统[M].北京:中国水利水电出版社,2009.
[2]徐绍娟,李冉,赵光宙. PMSM最大转矩电流比无速度传感器控制[J].电气传动,2011,41:(11):8-11.
[3]金宁治,王旭东,李文娟.电动汽车PMSM MTPA控制系统滑膜速度控制[J].电机与控制学报,2011,15(8):52-58.
[4]李长江,陈明俊,吴小役. PMSM调速系统中最大转矩电流比控制方法的研究[J].中国电机工程学报,2005,25(21):170-174.
[5]贺艳辉,王跃,王兆安.异步电机参数离线辨识改进算法[J].电工技术学报,2011,26(6):73-80.
[6]Zeraoulia M,Benbouzid M EI H,Diallo D. Electric Motor Drive Selection Issues for HEV Propulsion Systems:a Comparative Study[J]. IEEE Transactions on Vehicular Technology,2006,55(6):1756-1764.
[7]李军,余家俊.基于分段拟合的IPMSM最大转矩电流比控制研究[J].四川大学学报(工程科学版),2012,44(1):307-311.
[8]黄鹏,苗长云,黄雷,等.参数在线估算的永磁同步电机最大转矩电流比控制[J].煤炭学报,2011,36(1):172-176.
修改稿日期:2016-02-15
Motor Parameter Estimation and Maximum Ratio of Torque to Current Control Research
ZHU Guang,WANG Wenbai,DU Mingxing,WEI Kexin
(Tianjin Key Laboratory of Control Theory & Applications in Complicated System,Tianjin University of Technology,Tianjin 300384,China)
Abstract:Based on space vector control principle,control of permanent magnet synchronous motors by different d-q axis current allocation policy,used experimental data to estimate the motor parameters so as to achieve the maximum ratio of torque to current control. Experimental procedure and simulation results show that this method which estimate the motor parameters can be used to the maximum ratio of torque to current control,the control effect can be better,has some practical engineering.
Key words:permanent magnet synchronous motor;parameter estimation;maximum ratio of torque to current;space vector control
中图分类号:TM351
文献标识码:A
作者简介:朱广(1990-),男,硕士研究生,Email:zhu19900225@sina.com
收稿日期:2015-07-31

