高中数学与高中物理的内容结合点

邵秀芹，赵德刚

(山东省聊城市第一中学，山东聊城 252059)

最近，很多老师、同学或者家长都注意到这样一个问题：高中数学成绩不好的学生，即使在高中物理上学习非常努力，物理成绩也提高甚微。还有一些同学，高中数学成绩也可以，但是因为不能灵活地将高中数学知识运用到物理问题中来，所以解决物理问题的方法也不多，而那些善于运用数学方法来分析解决高中物理问题的同学却学得轻松自如。那么，高中数学和高中物理在内容上有哪些结合点呢？这里，我们重点介绍三角函数、不等式、极值、微积分在高中物理中的应用。当然，许多函数、几何知识、数列等知识在高中物理中都有非常重要的应用，在此限于篇幅，不一一赘述。

一、三角知识在高中物理中的应用

高中物理问题很多都涉及矢量，而矢量的运算遵循三角形法则，所以三角知识在高中物理问题中的应用非常广泛。比如：设一条河宽为，水流速度为，船在静水中的速度为，那么怎样渡河时间最短，最短时间是多少？

如图所示，设船头斜向上游与河对岸所成角度为，这时船速与y方向的分量为，而渡河所需时间为。由此可以看出，当v与l 一定时，随着的增大而减小；当时，即船头与河岸垂直时，渡河时间最短。

这说明，力学中的力的合成分解等都需要三角知识来解决。如果三角知识掌握得好，并将其灵活地运用到物理问题中来，解决物理问题会非常得心应手。

二、不等式在高中物理中的应用

在高中物理问题中，不等式也有自己的用武之地。例如下面是一个完全非弹性碰撞中能量损失最大化的问题。这个问题完全可以通过球碰撞前后能量的比较进行解决，方法是利用不等式知识进行直接求解。比如：如下图所示，有一个带正电小球，其质量为m=0.01kg，带电量大小为将其置于光滑水平面上的A点，当空间存在着斜向上的匀强磁场时，该小球从静止开始，始终沿着水平面做匀加速直线运动；当小球运动至B点时，可以测量到小球的速度为而此时小球的位移为m，求这个匀强电场取值的范围。

分析：为了使小球一直沿着水平面进行移动，电场力在竖直方向上的分力需要不大于重力，即：，所以有

三、极值在高中物理中的应用

极值方法在高中物理中的应用非常广泛，下面我们将通过一个常见的例子进行说明：质量为m的小球静止停放在光滑的 弧形轨道的点A上，圆弧轨道的半径为R，现在小球从点A开始运动，则这个小球从点A运动到点B的过程中，重力对小球做功的最大功率是多少？

问题分析：设小球从A点由静止并释放并运动到C点时的速度为v，根据机械能守恒定律

重力对小球做功的功率为

由上二式得

此时可以用极值法求的的最大值。令，则

要想使得最大，只需使得y最大。将两端同时取四次方，得

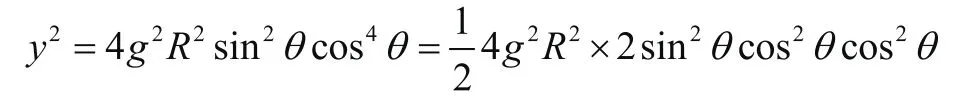
利用，且当且仅当时取得最大值。

四、微积分在高中物理中的应用

导数和积分作为高中数学的两个重要内容，是新课改以后出现的新内容。这两个内容在高中数学教材中出现已逾十年。而正因为导数在高中物理中的应用的广泛性，使得高中学生利用导数知识理解很多物理知识。比如：某物体做直线运动，位移对时间的变化规律为：，求物体运动的加速度和初始速度各是多少？

问题分析：由速度和导数的定义有

而初速度是t=0时刻的速度，将t=0代入上式得，而。

微积分思想也经常进行功率计算。功是一个基本的物理量，能量转化中经常能看到功率的身影。而正如我们所熟知，功是能量转化的一个量度。在实际应用中，我们经常会遇到变力做功的问题，或者是场力对连续介质做功的问题。我们通常采用这样的处理方法：首先是将力做功的过程或对象分解成无数微元，然后计算出各元功后再求和，一般来说，这一个求和过程经常需要依赖积分的计算。

通过上述分析我们知道，微积分思想在解决高中物理问题中的作用非常明显。比如瞬时速度、瞬时加速度、瞬时电流、电磁感应中的电磁感应势等问题。这种情况普遍存在于电学、力学以及一些综合性问题中。因此在物理教学中应加强微积分知识的渗透，在数学教学中应该加入一些物理背景，使得物理知识和数学知识的学习相得益彰。

当然，在解决物理问题中，用到的数学知识还有很多，由于篇幅所限，这里不再一一赘述。很多物理学家都是数学家。正是由于物理中提出的许多问题，使得物理学家们想到提出新的数学方法去解决它们。从某种意义上讲，物理问题的解决是数学发展的源泉和动力所在。

[1]高雪芬.一元微积分概念教学的设计研究[D].华东师范大学，2013.

[2]刘姣.基于高职学生职业发展的数学知识技能与相关信息技术研究[D].华东师范大学，2014.

[3]崔英梅.课程组织的量化分析研究[D].东北师范大学，2014.

[4]王芳.数学史融入导数教学的行动研究[D].华东师范大学，2012.