带齐次权的Hardy型不等式

应雪海，蔡光辉

（浙江工商大学统计与数学学院，浙江杭州310018）



带齐次权的Hardy型不等式

应雪海，蔡光辉

（浙江工商大学统计与数学学院，浙江杭州310018）

在采用Hoffmann-Ostenhof和Laptev构造权函数的思想，进行加权推广，给出了一类带齐次权的Hardy型不等式.利用Avkhadiev和Wirths得到的一维Hardy型不等式，运用放缩法，得到一类带余项的加权Hardy型不等式.获得的结论将Hoffmann-Ostenhof和Laptev中的相关结论推广至加权与带余项的情形.

Hardy型不等式；齐次权；余项

§1引　言

1920年Hardy得到积分型的Hardy不等式［1］：

其中等号当且仅当f（x）≡0时成立，（p/（p - 1））p是最佳常数.

有关Hardy不等式推广和改进的研究工作可以参考文献［2-6］.

Hoffmann-Ostenhof和Laptev［7］证明得到如下Hardy型不等式：存在τ＞0，使得对所有u∈下式成立

其中Φ是一类定义于Sd-1上的可测函数，满足即

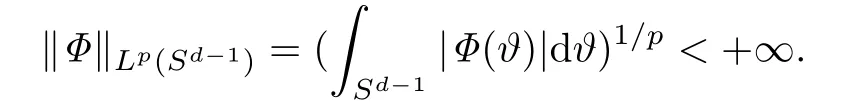
本文的主要目的是采用Hoffmann-Ostenhof和Laptev构造权函数的思想，进行加权推广，给出了一类带齐次权的Hardy型不等式.利用Avkhadiev和Wirths得到的一维Hardy型不等式，运用放缩法，得到一类带余项的加权Hardy型不等式.获得的结论将Hoffmann-Ostenhof和Laptev中的相关结论推广至加权与带余项的情形.

§2　引理

首先，引用文献［8］中关于在Lp（Sd-1）上薛定谔算子-△ϑ-Φ，Φ≥0的第一负特征值λ1的精确估计，其中-△ϑ是Sd-1中的拉普拉斯-贝尔特拉米算子，注意均需满足条件d≥3.

引理1［8］设d≥3，且0≤Φ∈Lp（Sd-1），其中p∈（（d - 1）/2，+∞）.则存在一个递增函

数β: R+→R+，当µ∈［0（p - 1）］时，

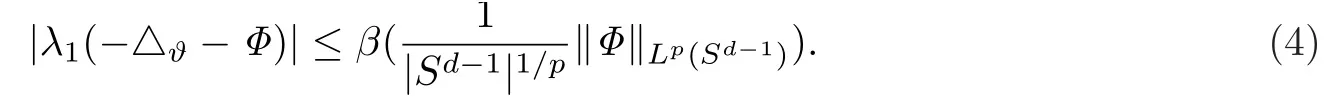
成立.

对任意非负、非平凡的函数Φ，可知λ1（-△ϑ-Φ）始终为负，再由变分原理及（4）式，可得

引理2设d≥3，0≤α≤d - 1，对于任意函数u（x）∈C0∞（Rd），则有如下加权Hardy型不

等式成立：

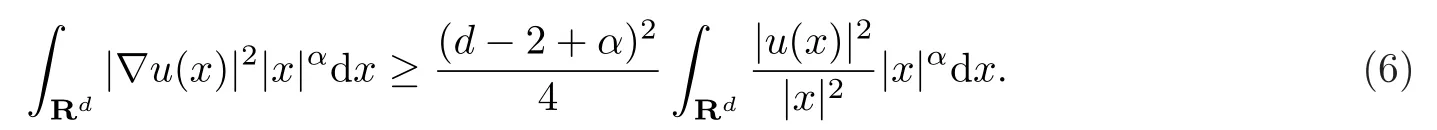
证运用散度定理，有

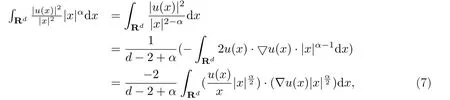
由（7）式和柯西-施瓦茨不等式，可以得到

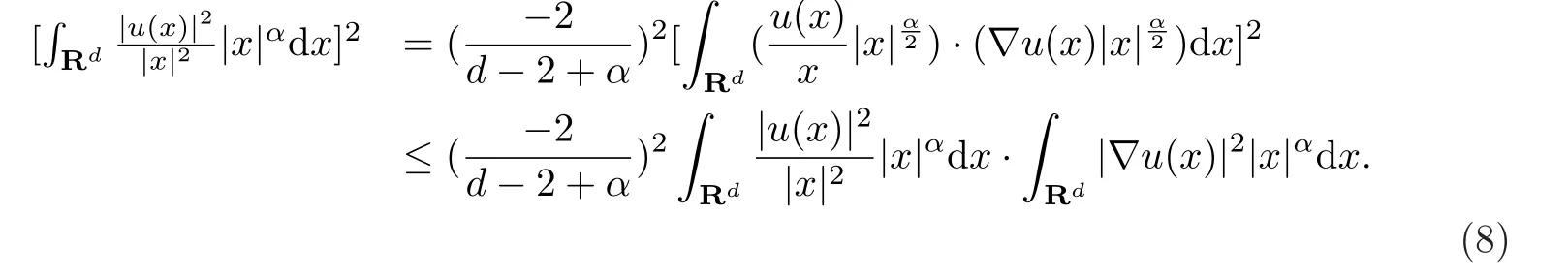
由（8）式，可得（6）式.至此引理2的证明完毕.

引理3设τ＞0，d≥3，且0≤α≤d - 1.则

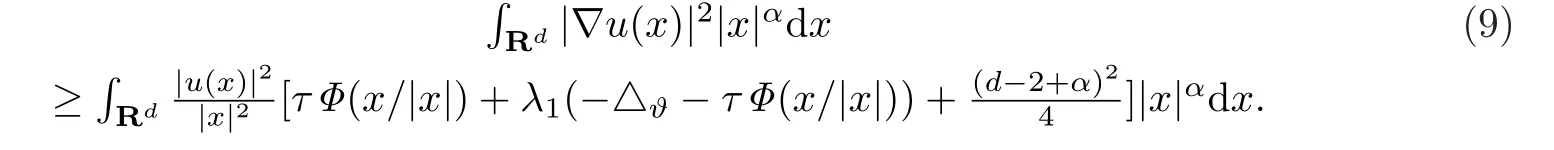
证令x =（r，ϑ）∈Rd，同时对积分进行极坐标变换，可得

对上式进行加权，可得

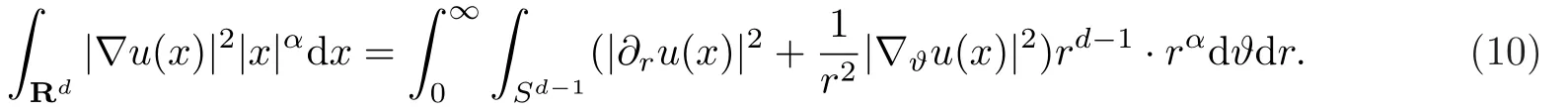
由引理2，有

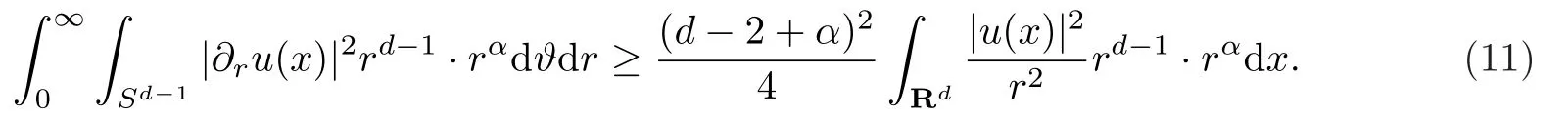
由引理1，可得

由（10）式，（11）式和（12）式，可得（9）式.至此引理3的证明完毕.

引理4设τ＞0，d≥3，0≤α≤d - 1且0≤Φ∈Lp（S）d-1，其中

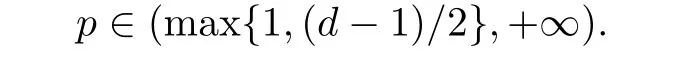
则

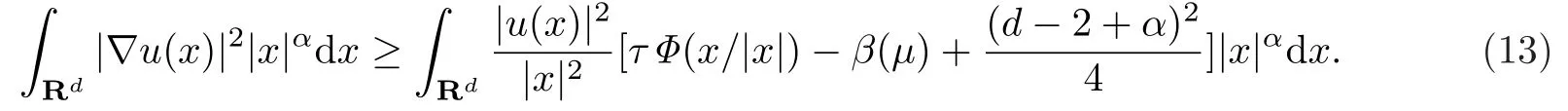
其中

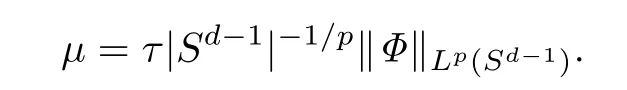
证对λ1（-△ϑ-τΦ）这一项运用（5）式进行放缩，可得

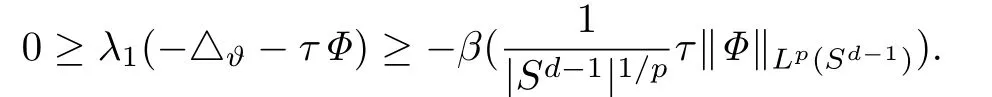
再将此与（9）式联列，有

令

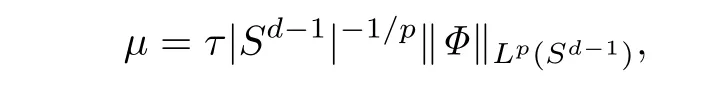
可得（13）式.至此引理4的证明完毕.

引理5设0≤α≤d - 1，对于任意函数f（x）∈H10（a，b），有

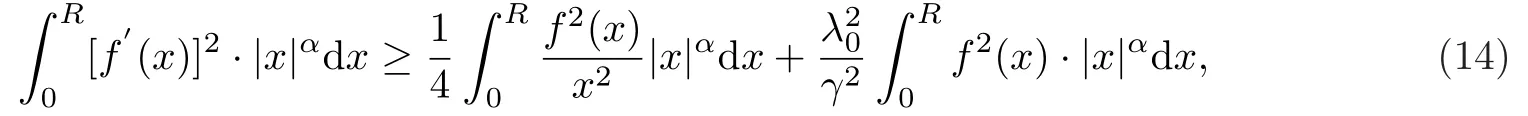
其中当且仅当f（x）≡0时等号成立，1/4和λ20/γ2均为最佳常数，λ0是Bessel函数中Lamb型等式

的第一正根，γ= R/2.

证令f（x）∈H10（a，b），γ:=（a + b）/2∈（0，+∞），由文献［9］的性质3，有

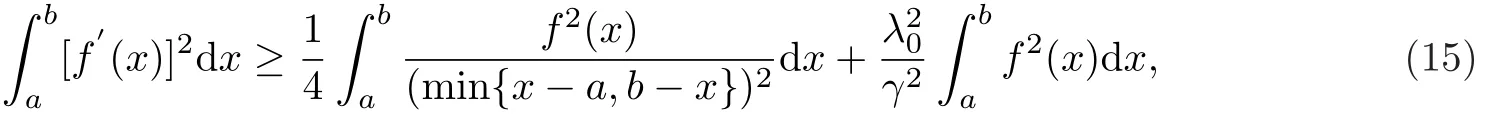
其中当且仅当f（x）≡0时等号成立，1/4和λ20/γ2均为最佳常数，λ0是Bessel函数中Lamb型等式

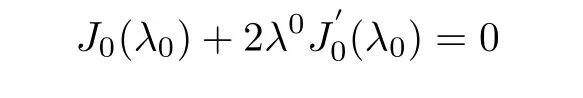
的第一正根，且λ0= 0.0940...

对（15）式进行放缩，可得

（a）当x∈（0，（a + b）/2）时，则x - a＜b - x，因此可得

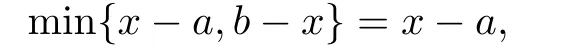
（b）当x∈（（a + b）/2，b）时，则

因此可得

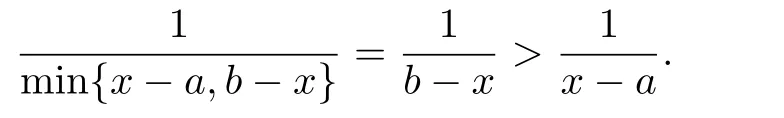
由（a），（b）和（15）式，可得

令α= 0，b = R，则可得γ= R/2，

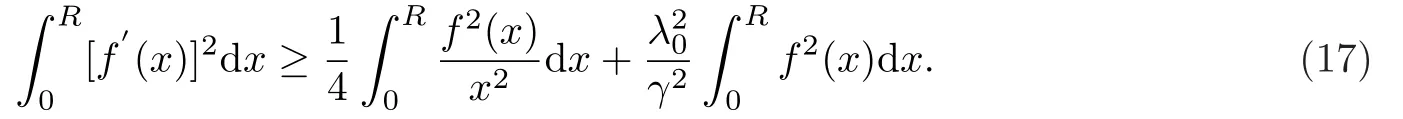
对（17）式进行加权推广，根据文献［9］中性质1和2的证明，可得

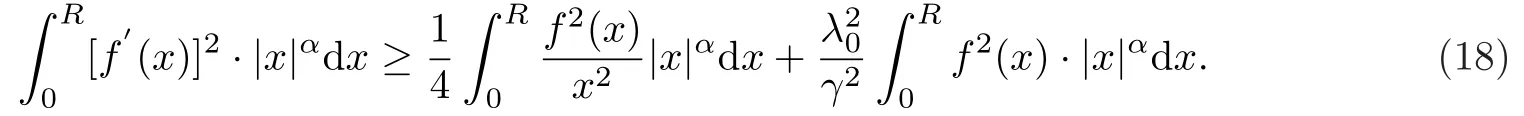
而（18）式即为要证明的（13）式.至此引理5的证明完毕.

§3　主要结果

定理1设d≥3，0≤α≤d - 1且0≤Φ∈Lp（Sd-1），其中

则

其中

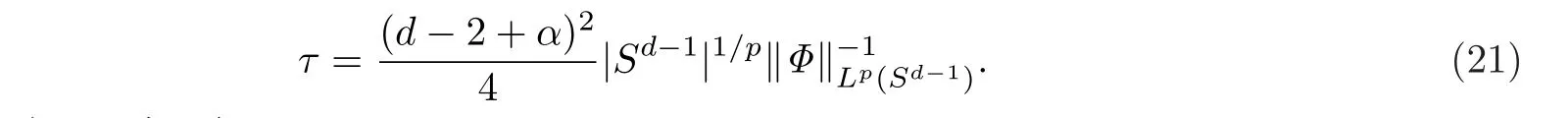
证由（19）式可得

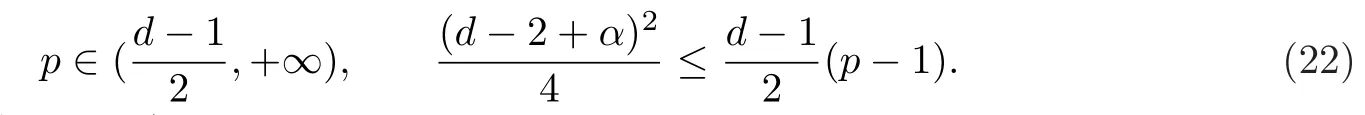
由（22）式，引理1及引理4，可得

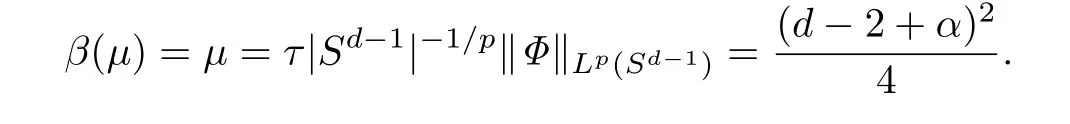
移项后得

至此定理1的证明完毕.

注1令α= 0，则由定理1，可得文献［7］中的定理1.1.

定理2设d≥3，0≤α≤d - 1且0≤Φ∈Lp（Sd-1），其中

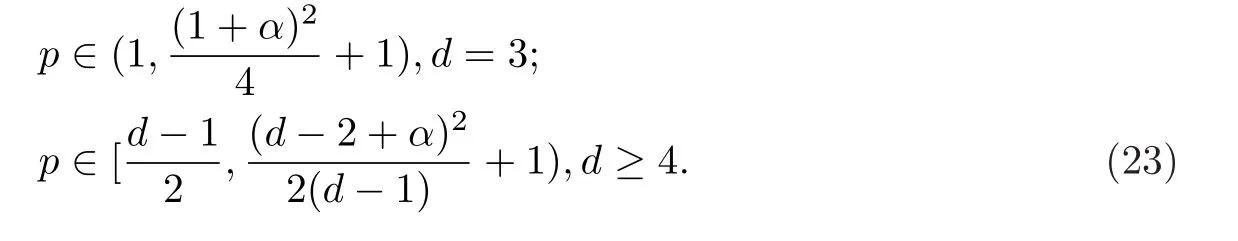
则有

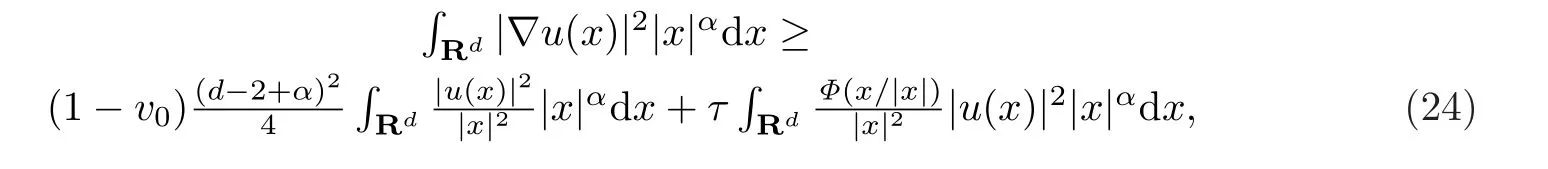
其中

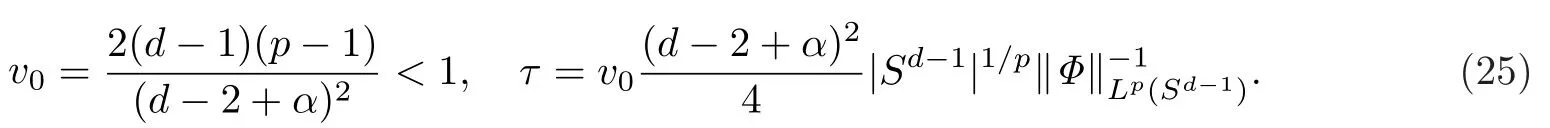
证由（23）式及引理1，可得

由引理4，可得

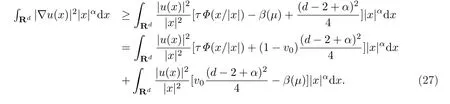
由（23），（26）及引理4，则有

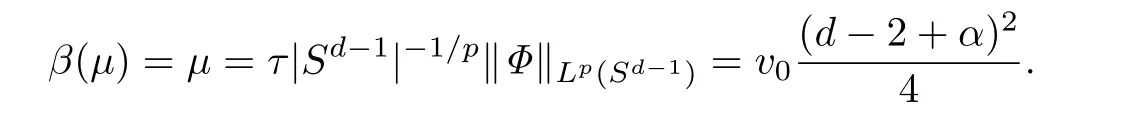
因此，有

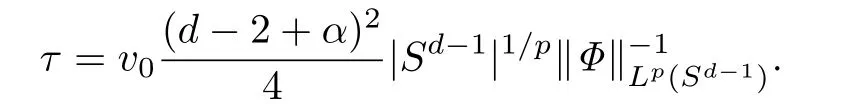
至此定理2的证明完毕.

注2若取

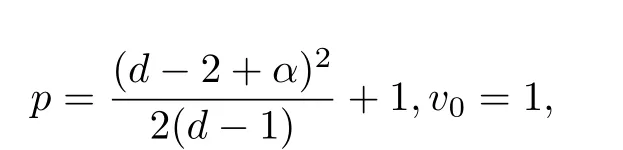
则由（24）式，可得（20）式.即由定理2，可得定理1.因此，定理2较定理1将文献［7］中的定理1.1推广至更加一般的情形.

定理3设d≥3，0≤α≤d - 1且0≤Φ∈Lp（Sd-1），其中

令Ω为Rd上有界闭区域，则

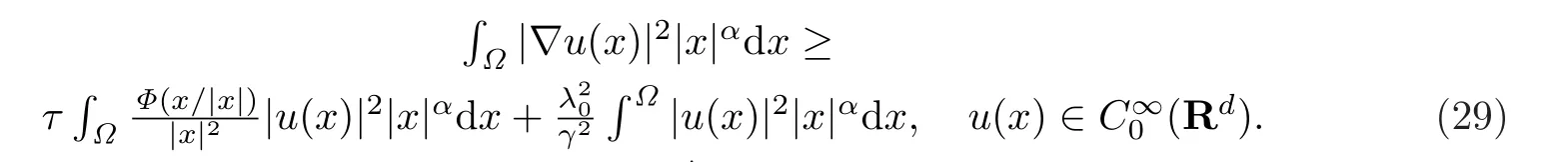
其中λ0是Bessel函数中Lamb型等式J0（λ0）+ 2λ0J′0（λ0）= 0的第一正根，γ= R/2，

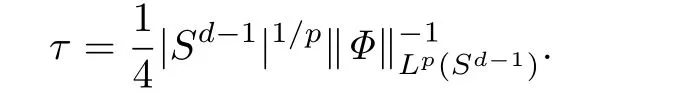
证由（28）式，可得

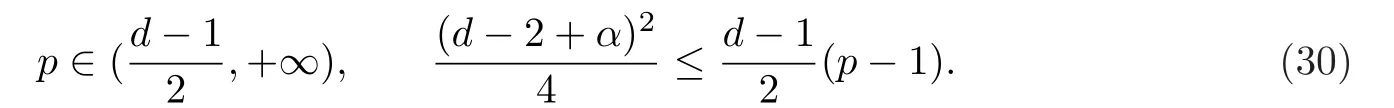
由（30）式，（10）式及（12）式，可得

（31）式在球域

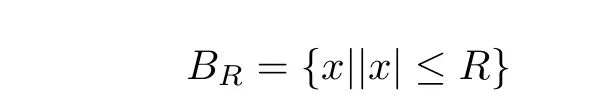
上成立，若取Rd上有界闭区域Ω，且Ω⊆BR（BR为包含Ω的最小球域），对于Ω外球域内进行零延拓

由（32）式，引理1及引理4，可得

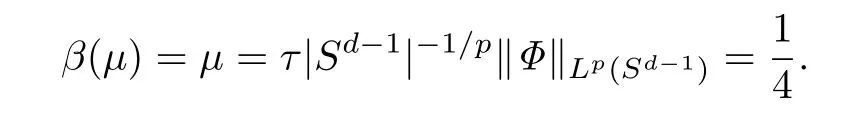
移项后，可得

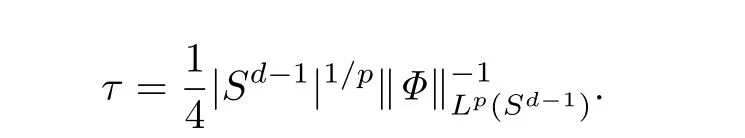
至此定理3的证明完毕.

注3定理3将Hoffmann-Ostenhof和Laptev中的定理1.1推广至加权与带余项的情形.

［1］Hardy G H. Note on a theorem of Hilbert［J］. Math Zeit，1920，6（3-4）: 314-317.

［2］孙保炬.关于有限和形式的Hardy-Hilbert不等式［J］.科技通报，2014，30（9）: 6-8.

［3］金永阳，韩亚洲. Heisenberg群上的一类带余项的Hardy型不等式［J］.数学物理学报，2011，31（6）: 1592-1600.

［4］何晓红.关于Hardy平均的一个不等式及其应用［J］.浙江大学学报（理学版），2015，42（2）: 133-141.

［5］Lewis R T，Li Junfang，Li Yanyan. A geometric characterization of a sharp Hardy inequality［J］. J Func Anal，2012，262（7）: 3159-3185.

［6］韩亚洲，金永阳，张书陶.各向异性Heisenberg群上一类Hardy-Sobolev型不等式［J］.高校应用数学学报，2010，25（4）: 440-446.

［7］Hoffmann-Ostenhof T，Laptev A. Hardy inequalities with homogeneous weights［J］. J Func Anal，2015，268（11）: 3278-3289.

［8］Doulbeault J，Esteban M，Laptev A. Spectral estimates on the sphere［J］. Anal PDE，2014，7（2）: 435-460.

［9］Avkhadiev F G，Wirths K J. Unified Poincare and Hardy inequalities with sharp constants for convex domains［J］. ZAMM-Z Angew Math Mech，2007，87（8-9）: 632-642.

MR Subject Classification: 42B

Hardy inequality with homogeneous weight

YING Xue-hai，CAI Guang-hui
（College of Statistics and Mathematics，Zhejiang Gongshang University，Hangzhou 310018，China）

Inspired by the ideas of Hoffmann-Ostenhof and Laptev，a class of Hardy-type inequalities with homogeneous weight are given. Using the one-dimensional Hardy-type inequality which has been obtained by Avkhadiev and Wirths，a class of weighted Hardy-type inequalities with remainder term are proved. The results obtained generalize the results of Hoffmann-Ostenhof and Laptev to the weighted and with the remainder term case.

Hardy type inequality；homogeneous weight function；remainder term

O178

A

1000-4424（2016）01-0109-07

2015-12-10

2016-01-18

蔡光辉，Email：cghzju@163.com

国家自然科学基金（11101364）；浙江省高校人文社科重点研究基地（统计学）