不可交易资产的平方套期保值问题
杨建奇,赵守娟
(1.湖南科技学院计算数学研究所,湖南永州425100;2.新乡学院数学系,河南新乡453003)
不可交易资产的平方套期保值问题
杨建奇1,赵守娟2
(1.湖南科技学院计算数学研究所,湖南永州425100;
2.新乡学院数学系,河南新乡453003)
提出并解决了不可交易资产的套期保值问题.基于金融实际构建了不可交易资产套期保值模型,在风险资产价格服从跳扩散模型的假设下提出了三个平方套期保值问题.借助于一个辅助过程和Hilbert空间投影定理,利用市场可观测量以后向形式给出了平方套期保值标准下的最优策略.最后通过Monte Carlo方法验证了套期保值策略的有效性.
不可交易资产;跳扩散过程;平方套期保值;效用最优
§1 引 言
金融风险管理是金融工程中一个重要研究课题。现有文献对其进行了大量的研究和讨论.然而仔细观察之后发现,大部分的文献研究(如[1-6])是在假定市场上的金融资产可以随时交易基础上进行的.然而,在现实的金融市场中存在许多不可交易资产,比如汇率就是一种典型的不可交易资产,由此导致的风险往往不能用可交易资产的方法来获得.一家中国公司在将来的某一时刻(比方说设为T)将收到以美元结算的一笔货款(设为K美元),由于人民币对美元的汇率(设为S)变动,它在T时刻实际得到的人民币收入将是H = kST,P-a.s.,汇率的升降变动将影响公司的实际收益,这家公司将面临所谓的汇率风险.公司应当采取何种策略来对冲这类风险,是管理层将不得不考虑的问题?再如在现代企业管理制度下,为调动管理人员的工作积极性,上市公司通常采取股权激励制度.在这种制度下,按照合同,公司的高级管理人员在约定时刻将收到一定数额的股票作为部分薪酬.对这些管理人员来说,他们担心的是股票的将来价格下跌,自己的终期收益将缩水.管理人员往往购买与公司业绩相关的其他风险资产进行投资,以降低收益风险.在实物期权理论中,某些不动产可以看成是一个不可交易资产.比如某公司为了稳定人心和鼓励职工安心为单位工作,规定职工工作T年后可以以市场价格的一定比例(k)来购买该住房,由于房地产价格受供求,政治和经济等因素的影响,房产价格的市场走势是不确定的,并且在T时刻前职工无权去买卖,因此可以把该住房看成是一个不可交易的风险资产S,到期后职工可以将该资产出售.因此为锁定将来的支出和收益风险,职工也面临着一个用可交易资产B对不可交易资产进行套期保值的问题.正因为如此,如何通过交易资产B来最大程度的消除风险成为金融理论和实践的一个重要问题.这些问题的共同特征就是如何定价这个不可交易资产以及采取何种交易策略来对冲不可交易资产所带来的风险.文献[7-9]就不可交易未定权益的定价问题进行了定量讨论.[10]讨论了利用通过不可交易资产寻找与之相关的可交易资产,从而达到给不可交易资产定价的问题.然而不可交易资产的套期保值的定量分析却鲜见于文献.[11]讨论了不可交易资产的套期保值问题,但其风险资产模型是扩散的.本文将假定风险资产的变化满足跳扩散模型,并在此基础上对不可交易资产的套期保值问题进行研究.首先建立一个不可交易资产的套期保值模型.然后以递推的形式给出具体的套期保值策略.最后利用Monte Carlo方法对冲策略有效性进行分析.
§2 市场模型的数学表达
用一个带流概率空间(Ω,F,F,P)来表示一个金融市场.假设W =(Wt)0≤t≤T是一个标准的实值Brownian运动,N =(Nt)0≤t≤T是强度为λt的Poisson过程. F =(Ft)0≤t≤T是由W和N生成的自然σ-域,并且满足通常假设: F =(Ft)0≤t≤T是右连续的(即0≤t≤TF0是平凡的,即其仅有所有的P - 0和P - 1集所组成.市场中所有的随机现象由(Ω,F,F,P)来刻画,有效的市场信息用σ-域F=(Ft)0≤t≤T来刻画,投资者在t时刻能够获得全部的有效市场信息为Ft,并在此基础上进行理性投资.
本文采用merton(1976)的经典跳扩散模型来描述风险资产的价格过程.假定市场中存在一种(0,T)内不可交易风险资产S和一种可交易资产B,其折现价格(以无风险资产价格过程为折现因子)St与Bt分别满足如下的随机微分方程
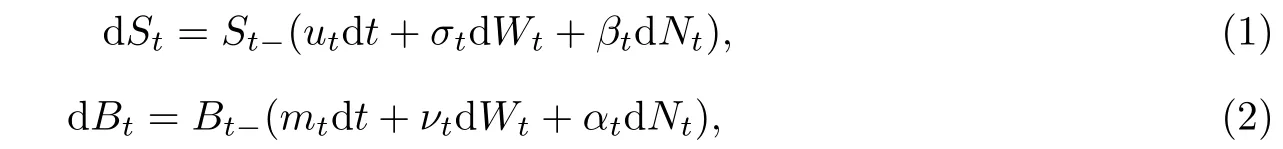
其中ut,σt,βt,mt,vt,αt是[0,T]到R的有界函数并且满足

定义1一个F可料的适应过程ϑ=(ϑt)0≤t≤T被称为交易策略,如果ϑ是F-可积的并且满足
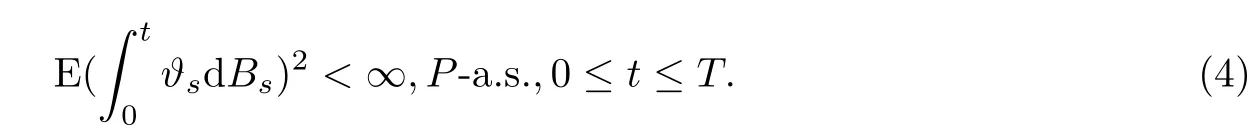
这样,前述的不可交易资产的风险对冲问题可以如下来描述.假定在T时刻,一个套期保值者一定会得到一个T-未定权益H且H = KST,P.-a.s.,如前所设St是不可交易资产,并且其T时刻的价格是随机的,所以套期保值者打算仅使用可交易风险资产B(比方说一个远期或期货合约).对该未定权益H进行套期保值,以降低未来收益风险. B,S往往是关系密切两种资产,如一段时期不可交易的房产与相关房产公司的股票等.由于市场的不完备性(因为市场中仅有一种可交易风险资产,随机因素却有两个),这个套期保值者利用自筹资策略不可能完全复制该未定权益,因而消不能完全消除因ST的随机性给他(她)带来的收益风险.通常说来这些套期保值者将基于三个方面来进行自己的投资:与自己终期目标财富的偏离程度最小;使自己的终期财富效用最优;在终期平均收益一定的情况下,损益风险最小.
显然,从风险管理的观点来看,风险对冲者的最终财富是ϑ的函数:
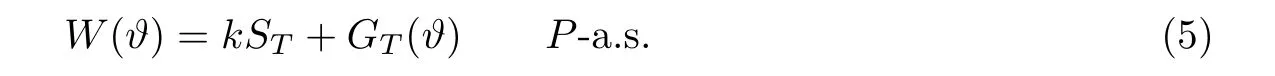
事实上,kST是风险对冲者在初始时刻明确知道将在T时刻将拥有的未定权益,而GT(ϑ)是风险对冲者的投资收益,它们之和就是风险对冲的最终财富.
在平方最优的框架内,风险对冲者面临的问题可以明确表述为如下三个问题:寻找分别满足下列条件的ϑ∈Θ.
注上述的三个问题(即优化目标)有着很好的经济学含义.问题1)中,L是一个预先给定的终期财富的目标水平,因此可以看成一个投资寻找最优策略使得终期财富与自己的目标财富偏差最小(把L-KST看成是风险对冲的对冲目标),则问题1)就是通常所说的均方最优风险对冲问题;问题2)中,函数u(w)是一个关于终期财富W的下凸函数,可以看做是一个效用函数,因此问题2)事实上可以看成终期效用最优问题.问题3)可以看成通常所说的均值方差问题,即在将来期望收益一定的情况下,风险最小(终期财富的方差看作是风险).
§3 最优套期保值策略
本节运用Hilbert空间的投影定理来对上述三个平方套期保值问题进行研究.众所周知,如果定义内积(X,Y)= E(XY)和范数||X,X|| =(EX2)12,则L2(P)是一个Hilbert空间,集合G(Θ)={G(ϑ)T,ϑ∈Θ}是L2(P)的线性闭子空间.因此优化问题1)等价于

其中Y = L - kST.
由Hilbert空间的投影定理知,X∗是(6)的解当且仅当(Y -X∗,X)= 0对所有的X∈G(Θ)都成立.因此可以得到最优策略的一个等价刻画.
引理2一个交易策略ϕ∈Θ是均方最优套期保值问题1)的解当且仅当对任意的交易策略ϑ∈Θ,如下等式总成立.
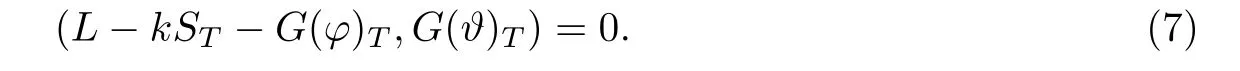
下面将首先考虑解决问题1),然后以问题1)的解为基础解决问题2)和3).为求解问题1),构造如下的辅助过程Z =(Zt)0≤t≤T:
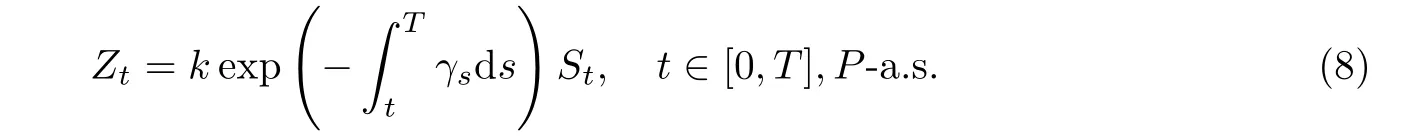
其中
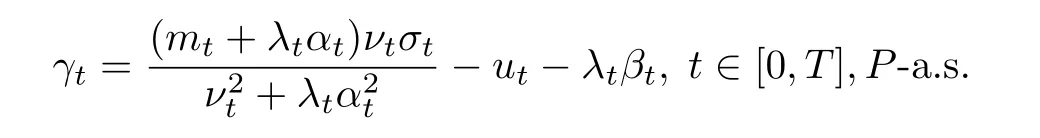
从(8)式可得ZT= kST,P-a.s.

其中
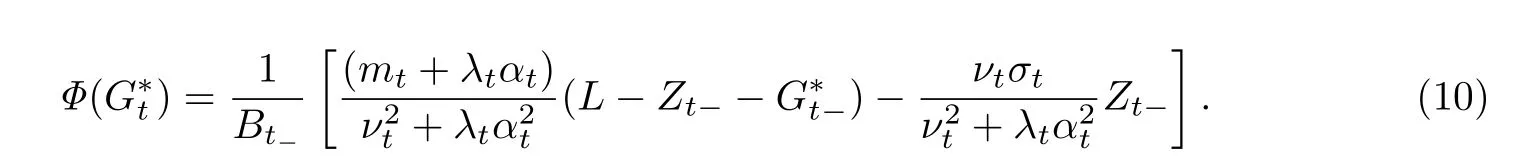
下面将证明ϕ就是问题1)的解.
为达到这个目的,定义如下内积函数Ht.
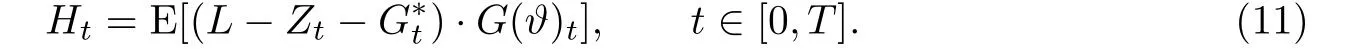
接下来证明Ht是一个特殊的常微分方程的解.
引理3设ϑ是任意一个交易策略,ϕ=Φ(G∗)是由(8)-(10)确定的投资策略,Ht由(11)来定义.则导数有定义并且

证由Itˆo引理知Z是如下随机微分方程的解.
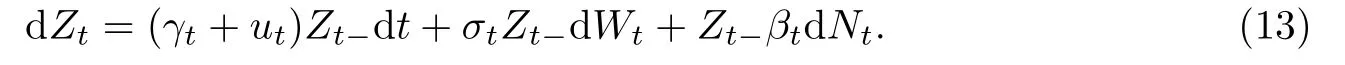
对Gt= G(ϑ)t,有
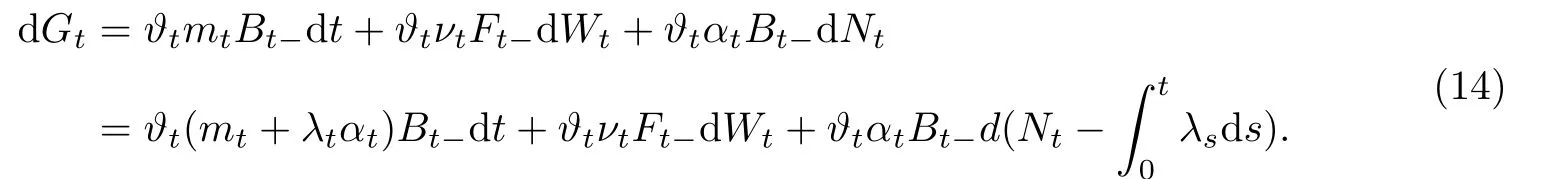
设Xt= ZtGt,由分部积分公式知
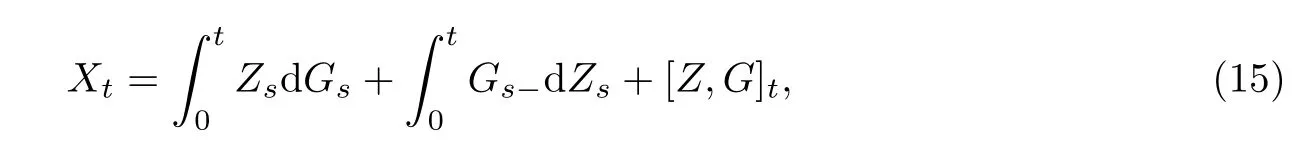
两边同时取期望,利用Fubini定理知
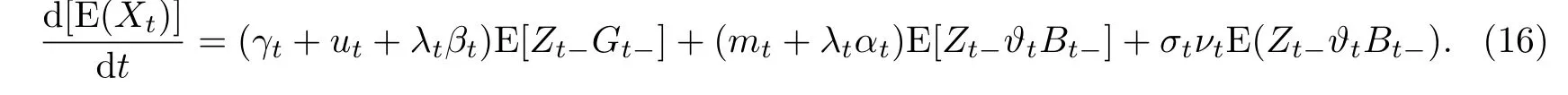
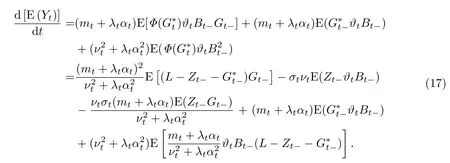
设¯Gt= E(Gt),则
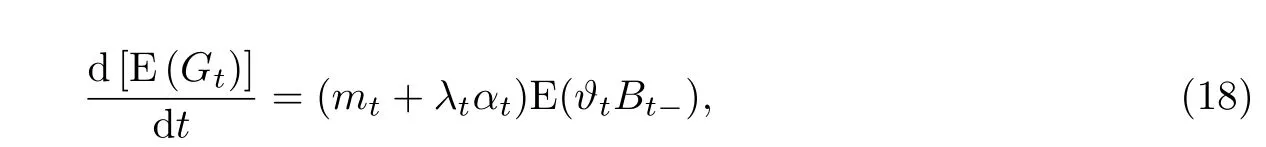
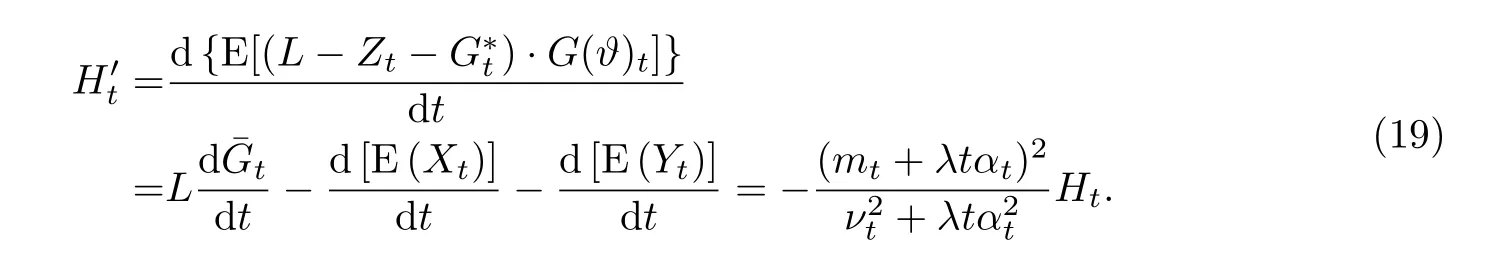
定理4在模型假设(1)和(2)下,均方最优套期保值问题1)的唯一解由下面的交易策略ϕ=来给出
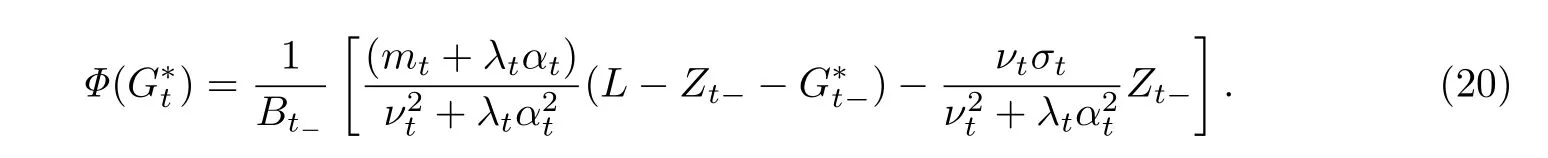
其中Zt由(8)来确定.
证由引理3知

注意到G0= 0,可得H0= 0.所以对任意的t∈[0,T]都有Ht= 0.特别的有HT= 0.考虑到ZT= kST,由引理2和Hilbert空间中正交投影的唯一性,可得定理4.
定理5在在模型假设(1)和(2)下,问题2)的解存在且由下式给出
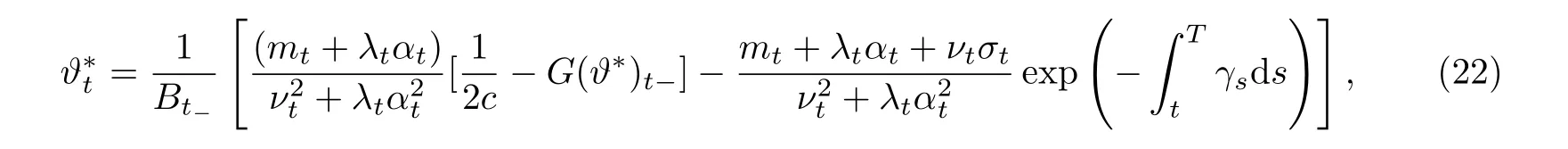
其中
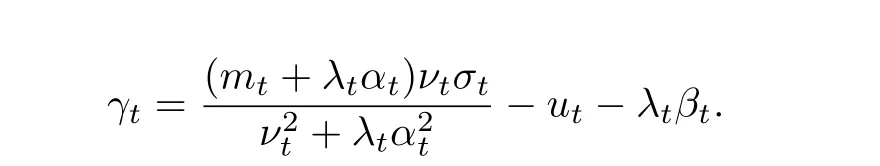
证令L = 1/2c,则问题1)变为
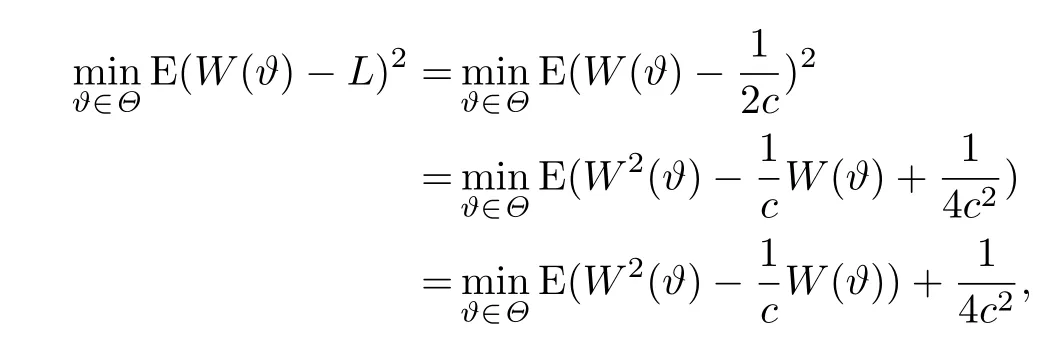
由于c是一个常值,因此问题1)转化为问题2).
将L = 1/2c代入(20)式,立即可得最优策略如(22),定理得证.
定理6对于给定的终期财富水平L,如果交易策略ϕ是问题1)的解,则ϕ一定是均方有效的(mean-variance efficient).
证设ϕ是问题1)的一个解且满足E[W(ϕ)]= m,m是一个预先给定的常数.假设还存在一个交易策略ϑ也满足E[W(ϑ)]= m,则

因此ϕ是均方有效的.
定理7设mt+λtαt= 0,ϕ(L)表示终期目标财富为L时问题1)的解,则问题3)的解为ϕ(Lm),其中

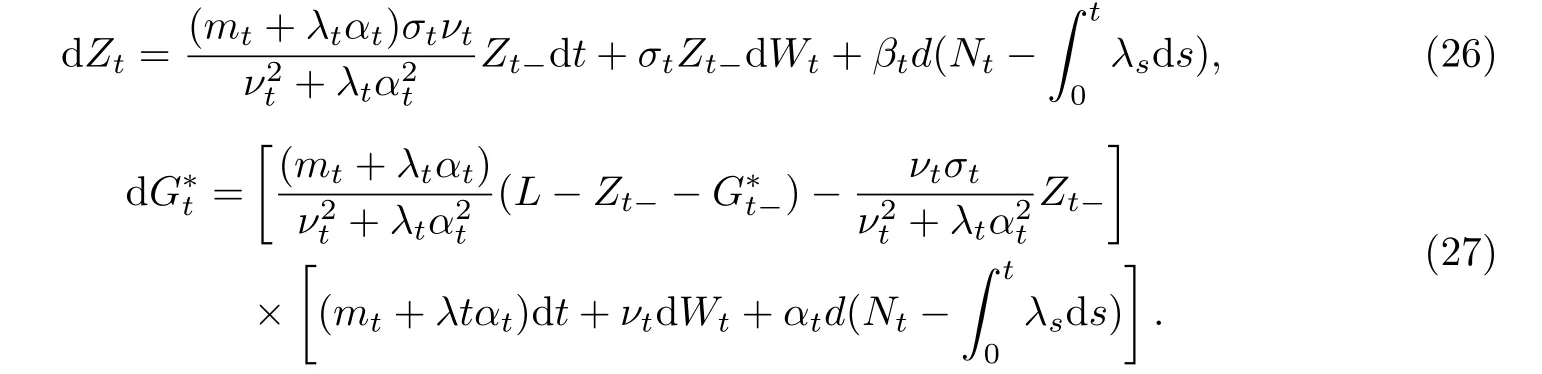
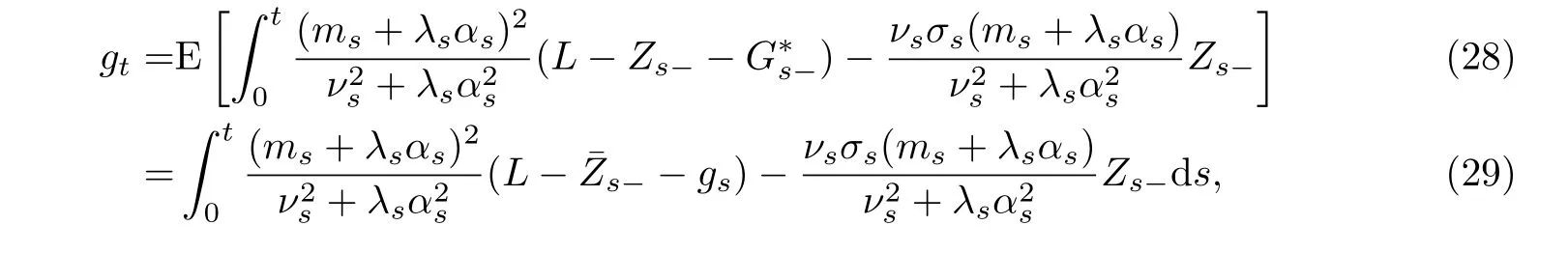
因而gt满足如下的常微分方程
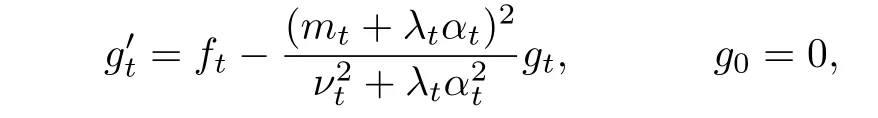
其中
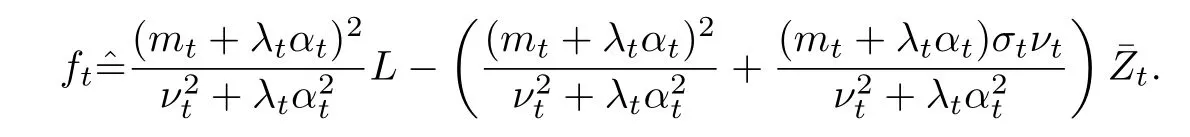
为记号简单,令

解这个常微分方程可得

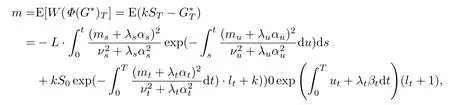
所以有
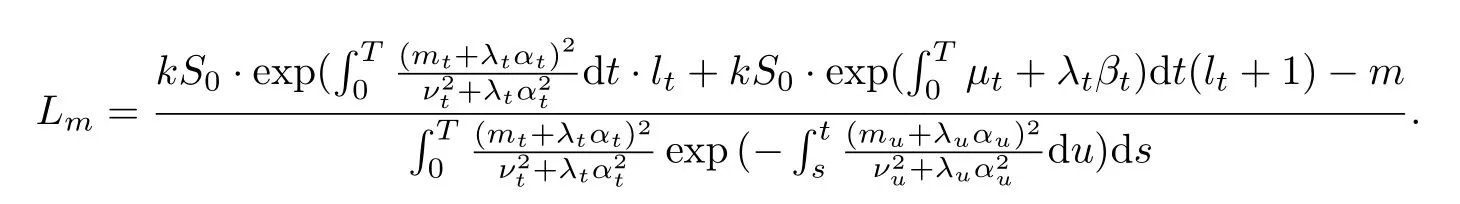
显然EW[ϕ(Lm)]T= m,因此ϕ(Lm)满足均值约束条件.由引理6知,ϕ(Lm)同样是方差最小的.注意到ϕ(Lm)是唯一的,因而问题3)的解也是唯一.定理得证.
结论分析与比较在文献[6]中给出了完全信息下的平方套期保值问题,但是从其文中公式(12)可以看到,尽管理论上该策略是存在和可以求出的,但是公式中涉及到的量(F¨ollmer-Schwweizer分解中的一些量),在市场实际中应用存在相当大的困难.与之比较而言,定理4-7分别给出了跳扩散模型下的平方最优套期保值策略,一个显著的特点就是策略中所含变量都可以在实际金融活动中观测到.具体的说就是t时刻策略由t-时刻的一些市场观测量来确定.从金融实际来说就是t时刻策略由此前一瞬间的市场观测量唯一确定了,在投资之前投资者可以根据已有市场数据直接决定自己的下一步投资策略,因此最优策略在实际中易于被操作.
§4 Monte Carlo模拟结果及分析
为检验对冲策略的有效性,来进行对采用对冲策略和不用对冲策略两种情况进行Monte Carlo模拟.下面在参数ut= 0.1,σt= 0.01,βt= 0.02,mt= 0.22,vt= 0.015,αt= 0.02,S0= 1,B0= 1.5的条件下是利用matlab7.01得到的结果:

表1 模拟次数:100

表2 模拟次数:1000

表3 模拟次数:10000
从表上可以看出,无论模拟次数多少,采用对冲策略后终期收益W(ϑ)与预期目标L的绝对偏差都要小于未采用对冲策略,收益的波动幅度也相对要小,这说明对冲策略是有效的,与预期目标的吻合程度要好;模拟次数的增加,收益的波动略有减少,这与实际相符.随着步长的减少,终期收益有上升的趋势,终期收益W(ϑ)与预期目标L的绝对偏差有减少的趋势,这说明根据风险资产价格的不断变化及时调整对冲策略能得到更好的对冲效果.
§5 结束语
本文对不可交易资产的风险对冲问题进行了研究.在跳扩散模型的假设下,利用投影定理及随机分析的方法,给出了三种不同标准下的对冲策略.一个优良特点就是策略完全由市场中的可观测量来表示,这个实际应用带来了相当大的便利.投资者可以通过市场历史数据及时调整自己的头寸,更好的管理自己的收益风险。最后利用随机模拟的方法,对最优策略的有效性进行了检验.尽管在跳扩散模型下得到了较为完美的结果,值得指出的一个问题是:如果资产价格不是跳扩散模型,此时的最优策略的后向递推形式将很难得到,此时采取何种手段来得到易于市场操纵的对冲策略还有待于更进一步研究.
[1]Biagini F,Cretarola A. Quadratic Hedging Methods for Defaultable Claims[J]. Applied Mathematics and Optimization,2007,56(3): 425-443.
[2]Schweizer M. Variance optimal hedging in discrete time[J]. Mathematics of Operations Research,1995,20(1): 1-32.
[3]Schweizer M. Approximation pricing and the variance optimal martingale measure[J]. The Annals of Probability,1996,24(1): 206-236.
[4]Gourieroux C,LAURENT H P,PHAM H. Mean variance hedging and numeraire[J]. Mathematical Finance,1998,8(3): 179-200.
[5]Pham H. On quadratic hedging in continuous time[J]. Mathematical Methods of Operations Research,2000,51(2): 315-339.
[6]Rheinl'nder T,Schweizer M. On L2projections on a space of stochastic integrals[J]. Annals of Probability,1997,25(4): 1810-1831.
[7]潘小军,林武忠.不可交易标的资产衍生证券定价问题[J].华东师范大学学报,2009(3): 19-24.
[8]曾健,陈俊荣.不可交易实物资产期权定价分析[J].当代财经,2004(1): 113-115.
[9]杨招军,宋昊,宋丹丹,等.基础资产不可交易条件下欧式期权的消费效用无差别定价[J].湖南大学学报,2012(12): 89-93.
[10]Duffie D,Richardson H. Mean2variance hedging in continuous time[J]. The Annals of Probability,1991,1(1): 1-15.
[11]陈金龙.实物期权定价与风险对冲问题[J].运筹学学报,2005(1): 82-88.
[12]Protter P. Stochastic Integration and Differential Equations[M]. New York: Springer Verlag,2004.
MR Subject Classification: 91B24;60H05
Quadratic hedging problems for non-tradable assets
YANG Jian-qi1,ZHAO Shou-juan2
(1. Institute of Computational Mathematics,Hunan University of Science and Engineering,Yongzhou 425100,China;2. Department of Mathematic of Xingxiang University,Xingxiang 453003,China)
The paper introduces and solves the hedging problems of non-tradable assets. Based on financial market practice,the non-tradable assets hedging model is constructed. Three meanvariance and quadratic hedging objectives are introduced on jump-diffusion model. The optimal hedging strategies,which are formulated by observable variables in backward form are given by an auxiliary process and Hilbert projection theorem. Finally the effectivity of the hedging strategies is tested via Monte Carlo.
non-tradable assets;jump-diffusion process;quadratic hedging;utility optimal
O211.6;F830.9
A
1000-4424(2016)01-0030-09
2015-04-25
2016-01-30
国家自然科学基金(71271136);2014年湖南省教育厅教改项目(481);湖南科技学院精品视频共享课程(概率论);重点学科建设项目(计算数学)

