求解随机广义纳什均衡问题的样本均值方法

王中兴

（沈阳职业技术学院，辽宁沈阳510665）



求解随机广义纳什均衡问题的样本均值方法

王中兴

（沈阳职业技术学院，辽宁沈阳510665）

研究随机广义纳什均衡问题.给出了随机广义纳什均衡问题变分不等式形式的再定式.利用期望残差最小化方法，获得了求解该问题的一种新的模型.并通过拟蒙特卡罗方法给出了该模型的求解方法.

随机广义纳什均衡问题；变分不等式；期望残差最小化；拟蒙特卡罗

§1　引　言

广义纳什均衡问题（generalized Nash equilibrium problem简记为GNEP）是标准的纳什均衡问题的一种推广.它考虑每个局中人的决策集都有可能与竞争者的决策集有关的情形.最近，由于其在不同领域都有着广泛的应用，广义纳什均衡问题引起了众多学者的关注.最早关于广义纳什均衡问题的研究是由Arrow，Debreu［1］和Debreu［2］给出的，他们把这类问题看作是一类抽象经济.更多的关于广义纳什均衡问题的研究成果可见［3-6］.

这里广义纳什均衡问题是有N个局中人的非合作博弈问题.以后把第v个局中人简单的记作v.用nv维向量xv表示局中人v的策略，其中nv为正整数.将所有局中人的策略用向量x =（x1，···，xN）∈Rn表示，其中n = n1+···+ nN，（x1，···，xN）:=（（x1）T，···，（xN）T）T.此外，当要强调局中某一特殊的局中人v时，也常将x表示成x =（xv，x-v），其中x-v为n-nv维向量（x1，···，xv-1，xv+1，···，xN），表示除局中人v以外的所有策略.为方便起见，记n-v= n - nv.广义纳什均衡问题是为了找到一个解x∗=（x∗，1，···，x∗，N），使得其中对每一个v = 1，···，N，x∗，v都是以下优化问题的解:

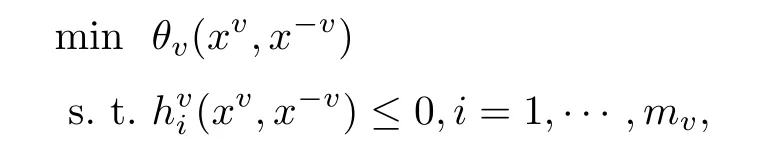
其中θv:，都是连续可微的，并且对每一个确定的x-v∈），i = 1，···，mv都是凸函数.为方便起见，对每一个v = 1，···，N，，i = 1，···，mv为分量的向量函数.值得一提的是上述优化问题的约束条件中含有其它局中人的策略x-v，这在实际应用中是十分必要的.如果对于每一个局中人，与其它局中人的决策相关的约束条件hv≤0不存在，那么广义纳什均衡问题就变成了经典的纳什均衡问题.

因为在实际应用中经常会有含有随机因素的问题，所以随机广义纳什均衡问题也引起越来越多学者的关注.如文献［7］中，Xu将随机Stackelberg-Nash-Cournot均衡问题再定式为带有互补约束的数学规划问题进行求解.

本文主要研究如下的随机广义纳什均衡问题（stochastic generalized Nash equilibrium problem简记为SGNEP）.即使得对每一个局中人v的决策变量x∗，v都是以下优化问题的解:

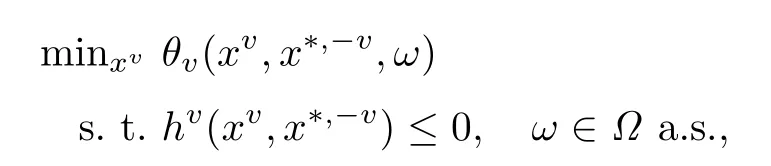
其中ω:Ω→Ξ⊂Rk是定义在测度空间（Ω，F，P）上的随机向量，并且“a.s.”是英文“almost surely（几乎真）”的缩写.

本文中假设样本空间Ω是非空紧集，并且概率密度函数ρ（ω）在Ω上是连续的.此外，还假定函数θv（xv，x∗，-v，ω）和hvi（xv，x∗，-v），i = 1，···，lv关于xv都是二次连续可微的，θv（·，x∗，-v，ω）是关于xv的拟凸函数，且θv（xv，x∗，-v，ω）关于ω也是连续的.

§2　随机广义纳什均衡问题的再定式

在给出求解随机广义纳什均衡问题的确定性的新模型之前，一方面给出随机变分不等式的定义.令S⊆Rn为非空闭凸集，（Ω，F，P）为概率空间，F为S×Ω→Rn的映射.随机变分不等式问题（Stochastic Variational Inequality Problem，简记为SVIP）

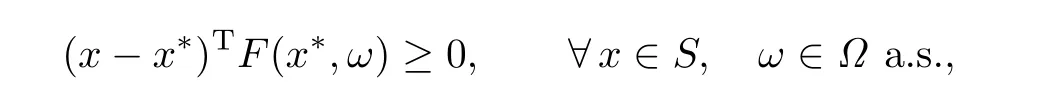
上述问题也记为SVI（F，S）.目前，关于随机变分不等式的研究较多，主要有样本路径优化方法，样本平均方法，随机近似方法，期望残差最小化方法等.

另一方面，选取一个参数α＞0和一个n×n对称正定矩阵G.定义SVI（F，S）的正则化价值函数g : Rn×Ω→［0，∞）为:

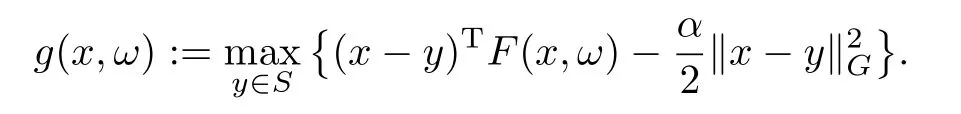
不难看出，对任意的x∈Rn和任意的ω∈Ω，

其中

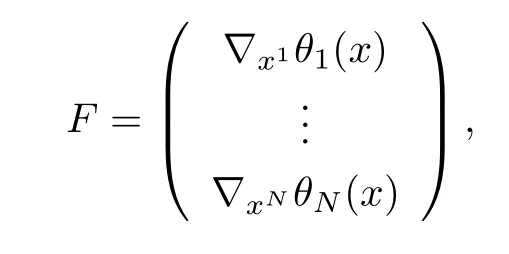
定理2.1令函数F : Rn→Rn为那么在本文给出的条件下，SVI（F，S）的解即为随机广义纳什均衡问题的解.其中，S :=

证设¯x是SVI（F，S）的一个解.令xv是满足约束hv（xv，x-v）≤0的任意一点.显然，y := （¯x1，···，¯xv-1，xv，¯xv+1，···，¯xN）T也满足上述约束条件.由于¯x是SVI（F，S）的解，有

再根据假设θv是拟凸函数及最小原理知，¯xv是随机广义纳什均衡问题的解.

基于以上事实，受Luo和Lin［8］利用正则化价值函数给出求解SVI（F，S）的期望残差最小化（expected residual minimization，简记为ERM）模型的启发，给出如下的求解随机广义纳什均衡问题的确定性模型.即找一个向量x∗∈S使它满足:

这里E表示关于随机变量ω∈Ω的数学期望，ρ:Ω→［0，∞）表示概率密度函数，它满足

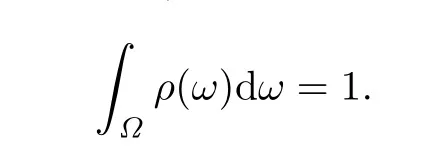
以后称上述问题为ERM模型或ERM问题.

特别地，由于这个ERM问题中含有一个数学期望.通常情况下，对数学期望求值是非常困难的，利用拟蒙特卡罗方法给出ERM问题的近似问题如下:

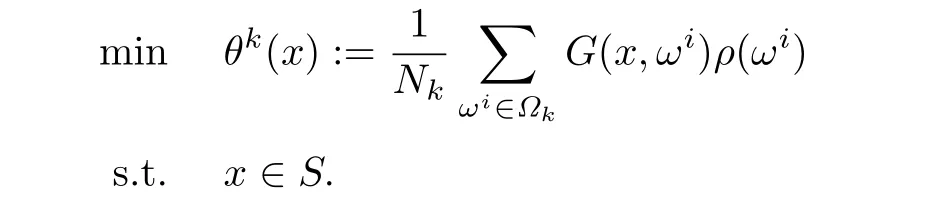
值得注意的是，根据拟蒙特卡罗数列的特点［9］，有如下结论成立:

§3　近似问题解的收敛性

定理3.1假设对每个k，xk是相应近似问题的解且x∗是｛xk｝的一个聚点.那么有x∗是ERM问题的解.

证不失一般性，假设limk→∞xk= x∗.显然x∗∈S.由▽xG在紧集S×Ω上的连续性可知存在常数C＞0满足

此外，根据中值定理可知对每个xk和每个ωi都存在

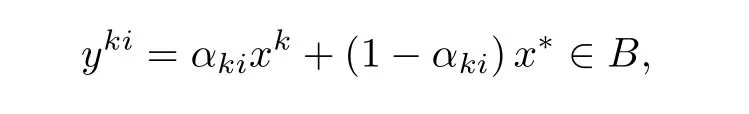
其中αki∈［0，1］满足

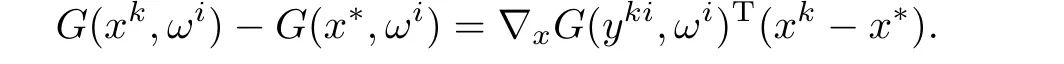
基于以上事实，有

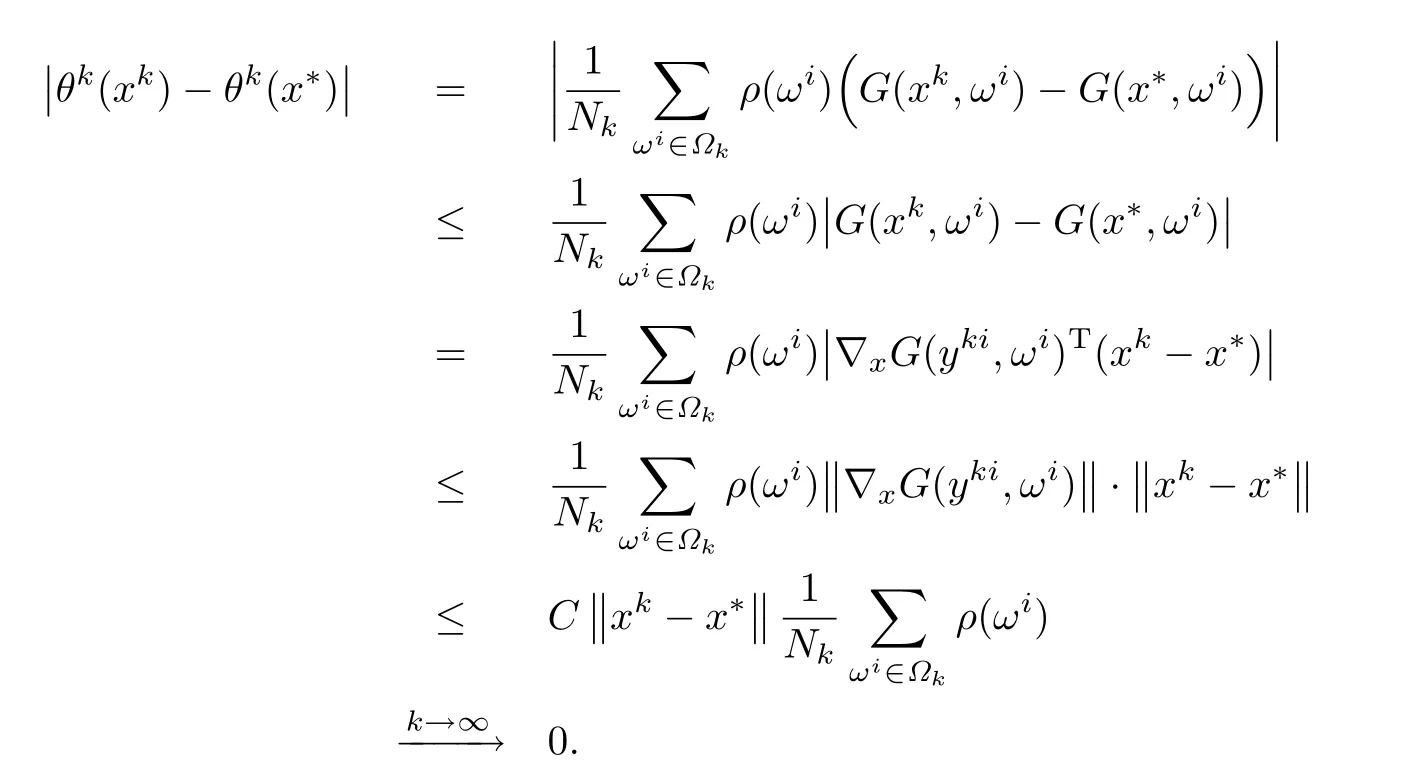
因为

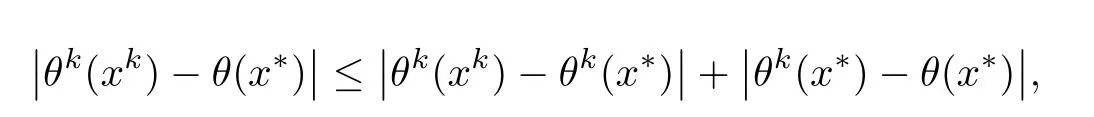
再由拟蒙特卡罗数列的特点及以上证明可得

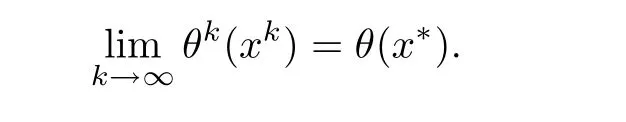
由于xk是近似问题的最优解，这就表示

上式两边都对k取极限，再根据拟蒙特卡罗数列的特点可得

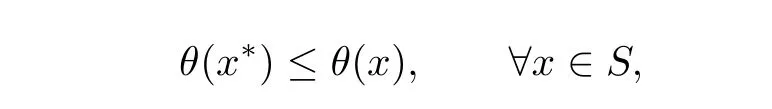
这就表示x∗是ERM问题的最优解.

§4　数值算例

基于［10］中的模型，本部分讨论关于大规模汽油市场中供应商竞争的随机广义纳什均衡问题.采用提出的ERM近似方法来解决这个问题.

考虑一个具有K个供应商的汽油现货市场，这K个供应商在市场需求未知的情况下以非合作的形式对汽油分配进行出价.逆需求函数p（q，ω）描述了市场需求，其中q是市场总供应，ω是一个随机变量.

市场需求确定之前，供应商v的供应量为qi.这个供应商的利润公式为

其中q-v表示供应商v的竞争者的总出价，q = qv+ q-v表示市场所有供应商的总出价，qvp（q，ω）表示供应商v的总收益，Cv表示供应商v的费用函数.由于供应商v的生产力与其他竞争者有关，并且可能会受到一些像随气候变化的汽油价格等不确定因素的影响，假定供应商v的约束为Gv（q，ω）≤0.此处，函数p（q，ω），Cv（qv）和Gv（q，ω）只关于qv局部Lipschitz连续.

每个供应商的目的都是在其他供应不变的情况下增加它的利润Rv.如果q∗，v，（v = 1，···，K）是如下问题的解

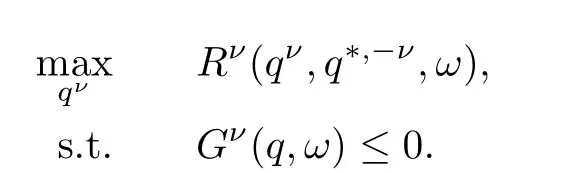
称（q∗，1，···，q∗，K）为一个随机广义均衡，这明显是一个SGNEP.因此，可以采用ERM近似方法来解这个问题.接下来，考虑以三个供应商为例给出数值算例.数据如下:

·逆需求函数为

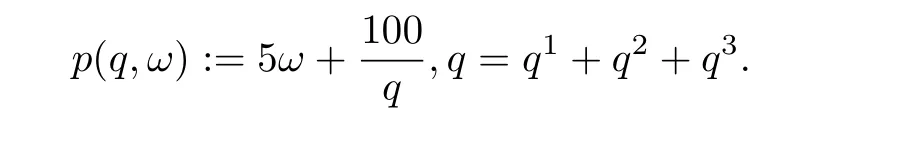
·费用函数为

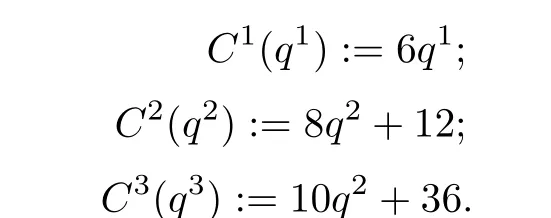
·约束为

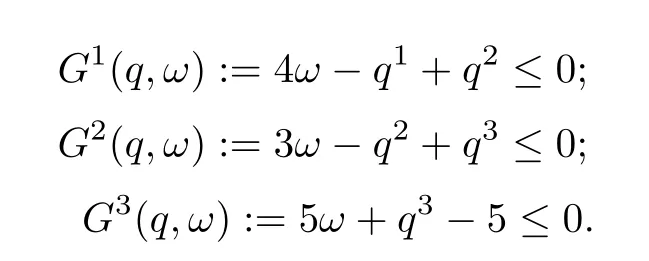
在上面的公式中，ω是［0，1］上的均匀分布随机变量.在这个例子中，用拟蒙特卡罗方法获得相应的近似问题.在试验中，用Matlab R2010a中的rand命令生成随机序列，并且用命令fminunc解近似问题.此外，选取初始点为（0，0，0）T.

在表1中，Ξ=｛ωτ|τ= 1，2，···，k｝中的k表示给定的样本大小.对于每一个给定的k，qk= xk表示此例中ERM近似问题的解.表1的计算结果显示至少对于试验的例子来说，ERM近似方法能够成功地解问题SGNEP.

表1　数值结果

［1］Arrow K J，Debreu G. Existence of an equilibrium for a competitive economy［J］. Econometrica，1954，22（3）: 265-893.

［2］Debreu G. A social equilibrium existence theorem［J］. Proceedings of the National Academy of Sciences of the United States of America，1952，38（10）: 886-893.

［3］Von Heusinger A，Kanzow C. Optimization reformulation of the generalized Nash equilibrium problem using Nikaido-Isoda-type functions［J］. Comput Optim Appl，2009，43（3）: 353-377.

［4］Pang Jongshi，Fukushima M. Quasi-variational inequalities，generalized Nash equilibria and multi-leader-follower games［J］. Comput Manag，2005，2（1）: 21-56.

［5］Facchinei F，Kanzow C. Generalized Nash equilibrium problems［J］. Ann Oper Res，2010，175（1）: 177-211.

［6］Facchinei F，Kanzow C. Penalty methods for the solution of generalized Nash equilibrium problems［J］. SIAM J Optim，2010，20（5）: 2228-2253.

［7］Xu Huifu. An MPCC approach for stochastic Stackelberg-Nash-Cournot equilibrium［J］. Optim，2005，54（1）: 27-57.

［8］Luo Meiju，Lin Guihua. Convergence Results of the ERM Method for Nonlinear Stochastic Variational Inequality Problems［J］. J Optim Theory Appl，2009，142（3）: 569-581.

［9］Niederreiter H. Random number generation and quasi-Monte Carlo methods［M］. Philadelphia: SIAM，1992.

［10］Li Peiyu，He Zhifeng，Lin Guihua. Sampling average approximation method for a class of stochastic Nash equilibrium problems［J］. Optimization Methods and Software，2013，28（4）: 785-795.

MR Subject Classification: 90C30

Sample average method for solving stochastic generalized Nash equilibrium problem

WANG Zhong-xing
（Shenyang polytechnic College，Shenyang 110045，China）

This paper is concerned with the stochastic generalized Nash equilibrium problem. A variational inequality form reformulation for SGNEP is proposed. Then by employing the expected residual minimization method，a new model is obtained to solve this problem. Finally，by using quasi-Monte Carlo method，this model can be solved.

stochastic generalized Nash equilibrium problem；variational inequality；expected residual minimization；quasi Monte Carlo method

O225

A

1000-4424（2016）01-0057-06

2014-11-25

2015-12-29