分析M/M/1多重工作休假排队的一种新方法
张宏波,郑群珍,史定华
(1.河南教育学院数学与统计学院,河南郑州450046;2.上海大学理学院,上海200444)
分析M/M/1多重工作休假排队的一种新方法
张宏波1,郑群珍1,史定华2
(1.河南教育学院数学与统计学院,河南郑州450046;
2.上海大学理学院,上海200444)
用一种新方法对经典的M/M/1工作休假排队系统建立模型.对该模型,用无限位相GI/M/1型Markov过程和矩阵解析方法进行分析,不但得到了所讨论排队模型平稳队长分布的具体结果,还给出了平稳状态时服务台具体位于第几次工作休假的概率.这些关于服务台状态更为精确的描述是该排队系统的新结果.
M/M/1排队;工作休假;GI/M/1型Markov过程;矩阵几何解;差分方程
§1 引 言
因为服务台休假可以使服务台的空闲状态得到有效的利用以免资源浪费,因而带有各种休假策略的排队模型在一些实际随机服务系统中有着重要的应用,成为排队论的一个研究热点.详细的介绍可以参见综述论文[1]或专著[2]及其中引用的文献.
Servi[3]最先引进了工作休假策略.在这种情形下,与普通休假不一样,在工作休假期,服务台不是完全停止工作,而是为在此期间到达系统的顾客以较低的服务率提供服务. Servi研究了多重工作休假的M/M/1排队,得到了平稳队长的PGF和平稳逗留时间的LST.后来,刘等[4]用拟生灭(QBD)过程与矩阵几何解的方法研究了该模型,得到了相应平稳指标的解析结果以及随机分解结构.另外,应用矩阵解析方法,田等[5]研究了单重工作休假的M/M/1排队,李[6],Baba[7]研究了顾客成批到达的M/M/1单重工作休假排队和多重工作休假排队.最后,对到达率或服务率服从一般分布的模型也有不少研究,例如,Baba[8]讨论了GI/M/1多重工作休假排队而Wu[9]讨论了M/G/1多重工作休假排队模型.最后,关于工作休假排队模型的详细介绍还可以参见综述文章[10].
对经典的M/M/1多重工作休假排队模型,在[4]中,把系统中的顾客数作为水平,把服务台的状态作为位相,作者对该排队系统建立了无限水平有限位相的QBD过程模型,因为这时服务台要么位于正规忙期,要么位于工作休假状态,所以这时建立的QBD过程的位相只取2个不同值.然而,对这样建立的模型,在分析系统的平稳特征时,对服务台的具体状态,只能得到服务台位于工作休假的概率.但对多重工作休假,因服务台可以进行多次休假,所以往往还关心服务台具体位于第几次休假(或已经进行了几次休假)的概率,这一问题用[4]中的模型无法回答.因此,在本文中,对该排队系统应用无限位相GI/M/1型Markov过程重新建模,通过对该过程求解,不但可得该模型的经典结果如平稳队长分布等,还对上述问题作了回答.所得新结果使得对服务台状态的刻画更为具体.
本文的主要贡献包括两方面.首先,用新方法对M/M/1多重工作休假建模,且对建立的无限位相GI/M/1型Markov过程,得到了平稳分布的解析结果;其次,得到了所研究排队系统的一些新结果,这些结果用[3]或[4]中的方法不能得到.在以下各节中,首先在§2给出所研究排队系统的一个新模型.然后在§3对模型求解,并对本文讨论的排队系统进行了分析.最后,§4是小结部分.
§2 模型描述
对经典的M/M/1多重工作休假排队系统,假设其到达率为λ而服务率为µ.另外,假设休假时间服从参数为θ的指数分布,且在休假期,系统为到达的顾客提供服务的速率为η,其中η<µ.
令L(t)表示时刻t时系统中的顾客数,用J(t)表示时刻t时服务台的状态,且规定J(t)= 0表示服务台位于正规忙期,而对k≥1,J(t)= k表示服务台位于工作休假状态且恰好位于第k次休假.现在考虑二维Markov过程{J(t),L(t),t≥0},其状态空间为
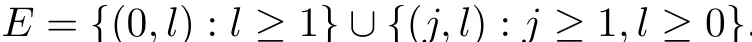
其中对l≥1,状态(0,l)表示服务台位于正规忙期且这时系统中有l个顾客;对j≥1及l≥0,状态(j,l)表示服务台位于第j次工作休假且系统中有l个顾客.
如果把状态按字典规则排序,则上述Markov过程的无穷小生成元具有如下所示的分块矩阵形式
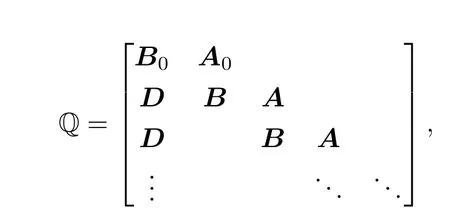
其中
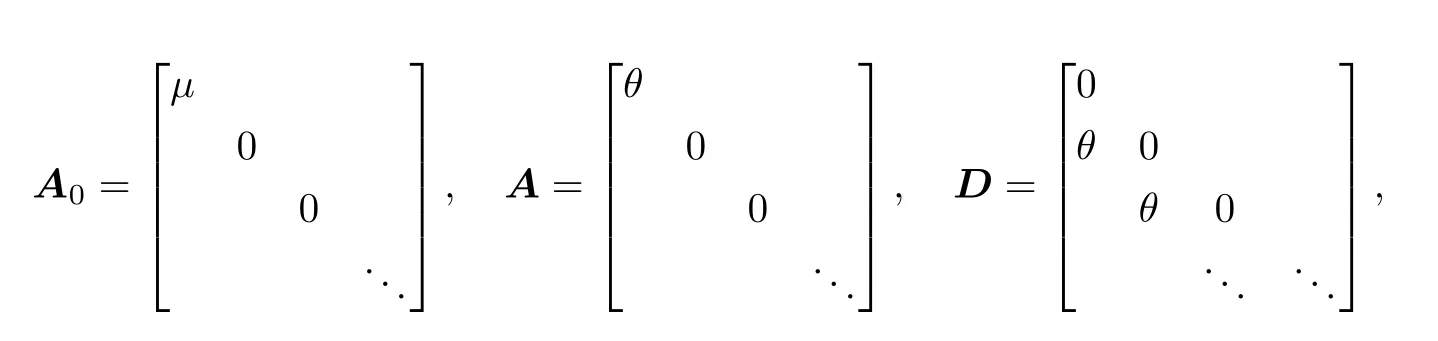
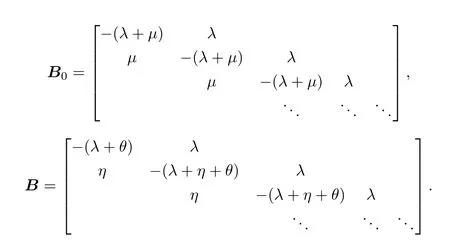
因此,所建立过程是一个无限位相GI/M/1型Markov过程[11-12].
由[3]或[4],当λ<µ时排队系统稳定,因而这时Markov过程{J(t),L(t),t≥0}的平稳分布存在.如果把平稳分布记为(π0,π1,π2,···,),其中分量π0=(π01,π02,···,)和
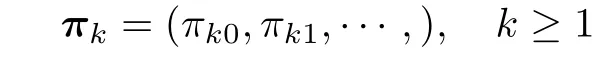
都是无穷维向量,则这时由[11-12]知平稳分布满足如下所示的算子几何解

其中R是一个无穷维矩阵,称为率算子且对本文所讨论的情形,它是下述矩阵方程的最小非负解

另外,初始向量π0和π1由线性方程组
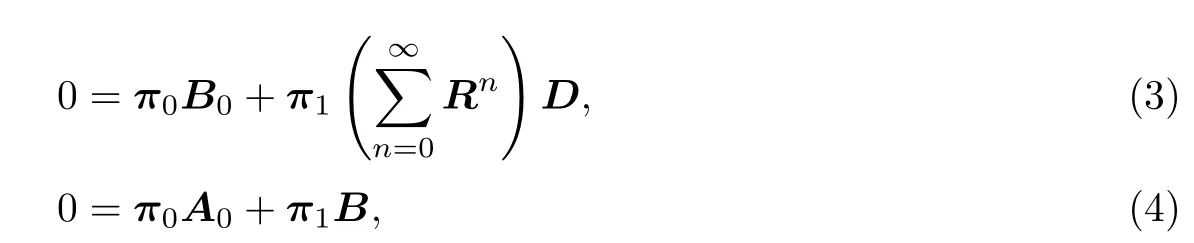
以及规一化条件共同确定.
§3 系统稳态特征分析
本小节对所建立的模型求解,并对排队系统的稳态特征进行分析.为了求解模型,首先给出率算子R以及初始分量π0和π1,有下述两个引理:
引理3.1率算子R的具体形式如下所示
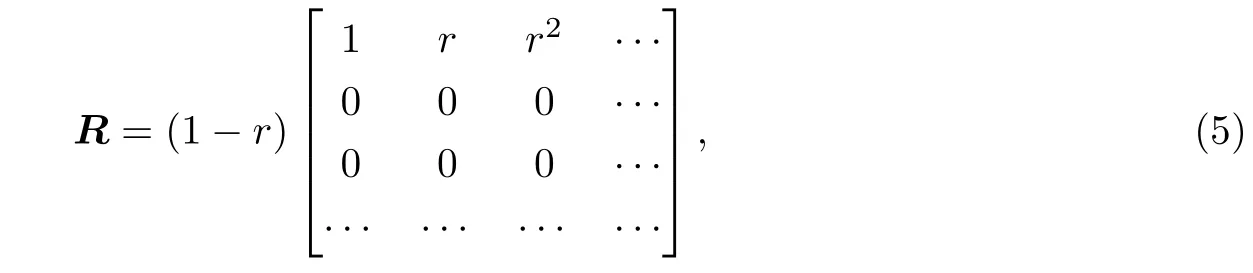
其中
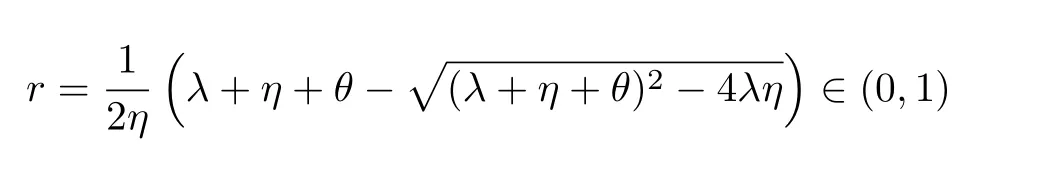
是一个常数.
证由率算子的概率解释[11]可知对本文讨论的模型,R除了第一行外其余各行元素皆为0.现在令(r0,r1,···)表示其第一行,则通过简单的代数运算可知方程(2)的分量形式为其中方程(7)是一个二阶线性齐次差分方程,且特征方程为ηr2-(λ+η+θ)r +λ= 0,从而易得两个特征根为因此
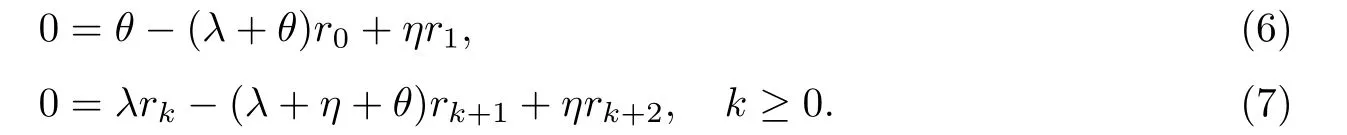
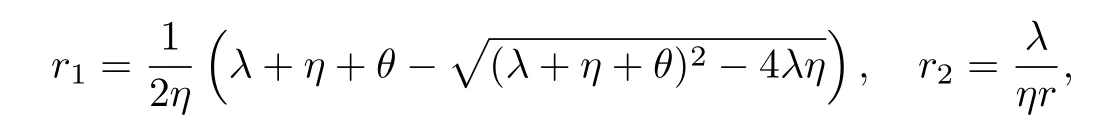
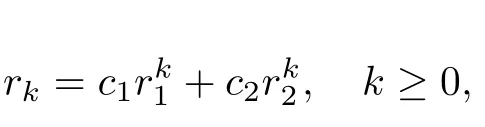
这里c1和c2都是待定常数.另外,由常规的代数运算容易验证r1∈(0,1),r2>1,所以为了得到方程(2)的最小非负解,常数c2必须为0,因而由(6)可知

其中由r1的定义可以验证上述最后一个等式成立.最后再把r1记作r即得引理结论.引理3.2如果λ<µ,则初始向量π0和π1由以下两式给出
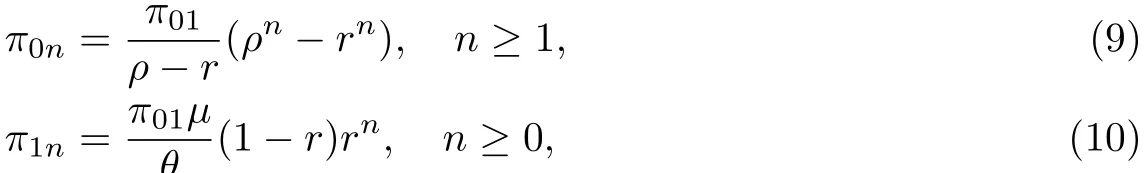
证前文已经指出,π0和π1满足线性方程组(3)和(4).现在,由(5)出发可以验证

所以有
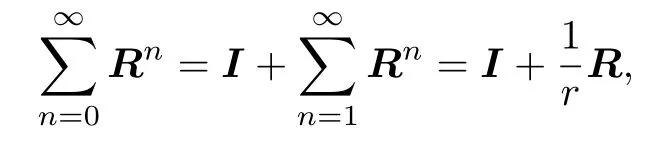
因而方程(3)的分量形式为
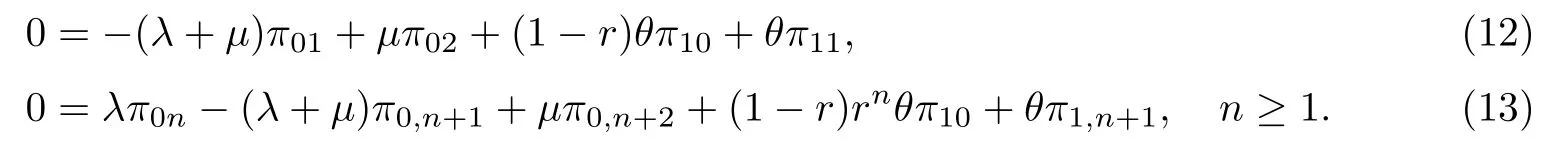
类似地,方程(4)的分量形式为
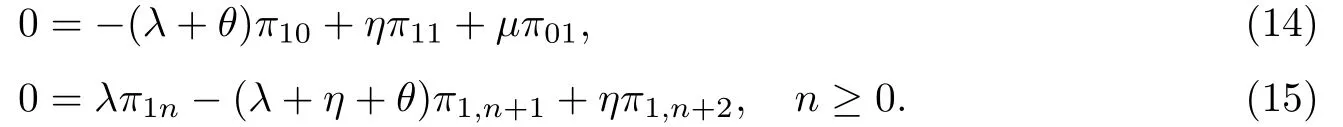
(是排队系统的交通强度.
方程(15)是一个2阶齐次差分方程,由类似于引理1中的方法可得其收敛解为

因而π11= rπ10,代入(14)可得π10(ηr -λ-θ)+µπ01= 0,再由(8)式又可得

由此即得(10)式.
最后,由π1n的表达式和(13)式可得

这是一个非齐次差分方程,且当λ<µ时,易求得其唯一收敛解为
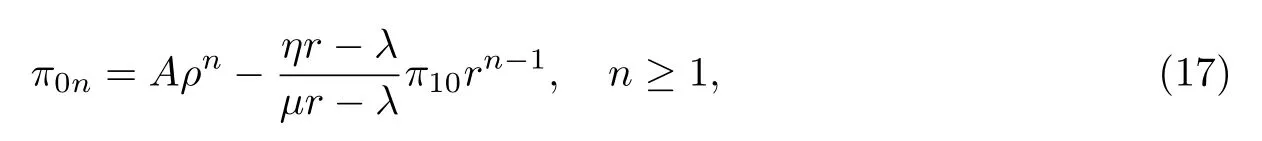
其中A是一个待定常数而ρ≜λµ.现在,令k = 1则有

所以由(16)可知
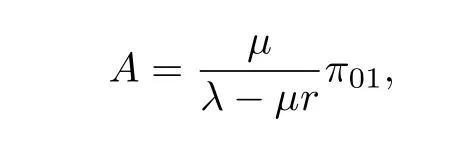
代入(17)并经过简单计算即可得(9)式.
在引理1和2的基础上,现在给出本文的两个主要结论如下:
定理3.1令bn表示平稳状态时服务台位于正规忙期且系统中有n个顾客的概率,令wk表示平稳状态时服务台位于工作休假状态且恰好处于第k次休假的概率,则有
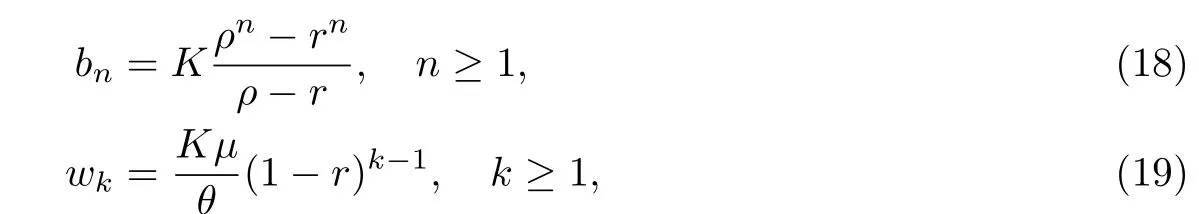
其中

是一个常数.
证首先给出所讨论Markov过程的平稳分布.由算子几何解(1)和(10),(11)两式,有
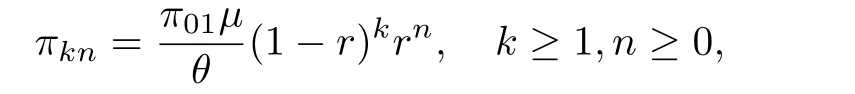

因此由规一化条件易求得最后,记π10为K,再由bn=π0n和wk=和引理3.2,可得定理的结论.
注3.1令pB和pW分别表示平稳状态时服务台位于忙期和工作休假状态的概率,则由定理3.1可知

通过直接验证知,这与[4]中所得结果一致.
定理3.2令L表示平稳状态时系统中的顾客数,则有

其中K的定义见定理3.1.
证由显然的事实
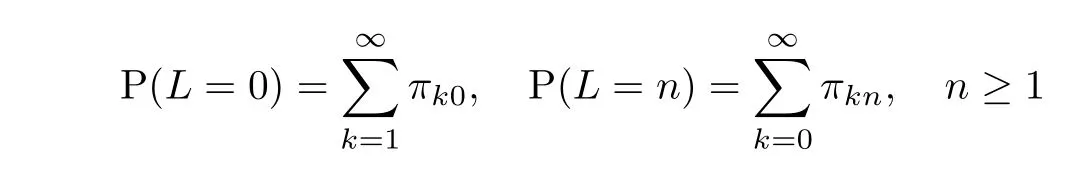
出发,经过计算易得.
注3.2在方程(20)的基础上,可以进一步讨论该排队模型平稳队长和平稳逗留时间的随机分解结果.然而这并不是本文的主要目的,相应的结论可以参见[4].
§4 小结
本文用一种新方法讨论了经典的M/M/1多重工作休假排队,给出了一些新结论,它们对排队模型平稳状态时服务台的状态进行了更为细致的刻画,因而具有重要的意义.
另外,应用本文方法还可以对其它M/M/1多重工作休假排队模型进行研究,如顾客成批到达或成批服务的排队,到达率或服务率依赖于当前系统中顾客数排队等,这些都是有意义的值得进一步研究的问题.
[1]Doshi B. Queueing systems with vacations-a survey[J]. Queueing Systems,1989,1: 29-66.
[2]Tian Naishuo,Zhang Zhe George. Vacation queueing models-theory and applications[M]. New York: Springer,2006.
[3]Servi L,Finn S. M/M/1 queues with working vacations(M/M/1/WV)[J]. Performance Evaluation,2002,50: 41-52.
[4]Liu Wenyuan,Xu Xiuli,Tian Naishuo. Stochastic decompositions in the M/M/1 queue with working vacations[J]. Operations Research Letters,2007,35: 595-600.
[5]Tian Naishuo,Zhao Xinqiu,Wang Kaiyu. The M/M/1 queue with single working vacation[J]. International Journal of Information and Management Sciences,2008,19: 621-634.
[6]Li Jihong,Zhang Zhe George,Tian Naishuo. Analysis for the MX/M/1 working vacation queue[J]. International Journal of Information and Management Sciences,2009,20: 379-394.
[7]Baba Y. The MX/M/1 queue with multiple working vacation[J]. American Journal of Operations Research,2012,2: 217-224.
[8]Baba Y. Analysis of a GI/M/1 queue with multiple working vacations[J]. Operations Research Letters,2005,33: 201-209.
[9]Wu Da,Takagi H. M/G/1 queue with multiple working vacations[J]. Performance Evaluation,2006,63: 654-681.
[10]Tian Naishuo,Li Jihong,Zhang Zhe George. Matrix analytic method and working vacation queues- a survey[J]. International Journal of Information and Management Sciences,2009,20: 603-633.
[11]Miller D R. Computation of steady-state probabilities for M/M/1 priority queue[J]. Operations Research,1981,29: 945-958
[12]Li Quanlin. Constructive computation in stochastic models with applications,the RG-factorizations[M]. Beijing: Tsinghua University Press,2010.
MR Subject Classification: 60K25;90B22
A new approach for analyzing the M/M/1 queue with multiple working vacations
ZHANG Hong-bo1,ZHENG Qun-zhen1,SHI Ding-hua2
(1. School of Mathematics and Statistics,Henan Institute of Education,Zhengzhou 450046,China;
2. College of Sciences,Shanghai University,Shanghai,200444,China)
A new approach to model the M/M/1 queue with multiple working vacations is provided. By the GI/M/1 type Markov process and matrix analytic method,the explicit expression for the stationary queue length distribution is given firstly. Furthermore,the probability of the exact number of vacations that the sever has taken is also obtained. The more accurate descriptions for the status of the server are new results for the queue model.
M/M/1 queue;working vacation;GI/M/1 type Markov process;matrix geometric solution;difference equation
O226
A
1000-4424(2016)01-0050-07
2015-12-06
2016-01-03
国家自然科学基金(61174160);河南省高等学校青年骨干教师(2014GGJS-136);河南省高等学校重点科研项目(16A110002);河南省教育厅教师教育研究课题(2015-JSJYYB-118);河南省大中专就业创业研究课题(JYB2015042)

