浅谈《高等数学》的课堂教学

张郑芳（杭州电子科技大学理学院，浙江杭州310018）



浅谈《高等数学》的课堂教学

张郑芳
（杭州电子科技大学理学院，浙江杭州310018）

摘要：文章从教学内容，教学方法，教学形式三方面阐述了《高等数学》教学过程中的建议。

关键词：理论；计算；延伸

Abstract：In this paper，three aspects of the suggestions in the process of the course of Advanced Mathematics are given，including the contents of teaching，the methods of teaching and forms of teaching.

Key words：theorems；calculation；extension

自2011年开始《高等数学》课程的教学以来，从课堂教学的体验、学生的交流反馈以及名师课堂的学习等过程中，以青年教师的角度，以“教学花心思，学生乐学”为宗旨，有如下几点建议。

一、教学内容：理论与计算并重

（一）理论是基石

《高等数学》中存在大量的定义、引理、定理、推论，需要学生先理解后记忆。而学生往往对定义比较轻视，对定理的证明又一知半解，因此缺乏较扎实的理论基础。在实践中，由于对数学本质的知识内容无法理解透彻，碰到稍微综合的题目，就容易出现思路模糊，一错再错的情况。

在这个问题中，学生需要弄清楚的是导数的定义和连续函数的定义。由于学生在中学时已经学习了一些初等函数的求导公式，碰到计算题往往不假思索，匆匆下笔，最终迷失在解题的过程中。通常错误的做法是，先对函数非零处的表达式利用求导公式求导，然后再对导函数求极限，由于极限不存在，得出函数在x=0处导数不存在的结论。这里所犯的严重错误就是对函数导数的概念不清晰、理解不到位所致。中学里学习的求导公式是针对初等函数而言的，而分段函数不是初等函数，因此在分段点处的导数只能通过定义来证明其是否存在。正确的做法为在非分段点处使用求导公式，而在分段点处则用导数的定义进行计算求解，因此，正确的导函数应为

接下来本题的第二问，由于做了一步求导的运算，学生不大容易接受导函数仍是函数这个概念，加之对连续函数的定义理解不清晰，往往出错率较高。如果把导函数作为一个普通的函数，让学生从函数连续性的定义出发，来分析这个函数在x=0处的连续性，学生思路会清晰得多，正确率也会高很多。因此，重视定义、定理的理解，应该是打破中学结论式的习惯性思维，构建系统的、分析的数学思维的重要突破口。

（二）计算是应用和推广

数学的技巧和结论，只有与各专业的背景相结合并解决实际问题，才能体现出数学作为工具的重要性。开设《高等数学》课程的目的，大致也在于此，并且《高等数学》绝大部分课时，也集中在计算方法的学习和练习上。通过计算题的习练，可以加深对定义和定理的理解，对计算方法的熟练，进而在方法和技巧上进行创新，对解决实际问题提出思路和建议。目前，大多数学生《高等数学》挂科的原因往往与自己动手练习较少有关。即使学生能够听懂教师课堂所讲的内容，但课后不进行练习巩固，也很难真正消化课堂所有内容，就算是简单的利用公式求解的题目，也会输给公式。

该问题的第一问，如果熟知arctant和sect的求导公式，利用参数方程的求导法则，出错率不高。而学生往往对一些中学时期没有接触过的三角函数的求导公式记忆比较生疏，因此在求解此类问题时就显得无从下手。在理解的基础上，只有通过适量的练习，才能将这些公式固化为自己的知识记忆。也就是说，练习有助于公式的记忆。

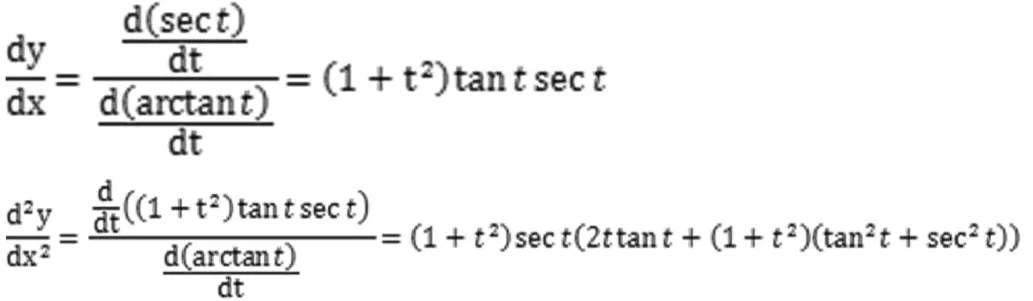
二、教学方法：详略得当，重点突出

（一）理论证明部分详略得当

在《高等数学》的理论部分，有相当一部分是有关定理的证明。当定理证明的文字稍长，学生阅读课本或者看板书时非常吃力，缺乏耐心。而定理的证明是理论成立的严格性保障，如果在课堂上省略证明过程，则对定理的理解会显得空洞无力，底气不足。因此详略得当的安排定理证明的讲解，特别是当讲解的内容以理论居多的课时，显得尤为重要。一个较好的授课策略是：对基础性的、先源性的定理作详细的展开讲解，而对推导式的、改进式的定理作简略且突出关键点的引导。譬如，在讲解三大微分中值定理时，可以详细的介绍罗尔定理的证明，并给出其三个条件缺一不可的反例。其次，讲解拉格朗日中值定理时，引导学生构造函数，并应用罗尔定理给出证明。最后，讲到柯西中值定理时，学生基本上能沿着前一个思路去构造函数，并验证罗尔定理的条件给出证明。这样的安排，对教师而言，三大微分中值定理的讲解处理得环环相扣，详略得当；对学生而言，则可以从定理的证明过程中，积累一定的证明技巧。

（二）强调关键步骤，突出重点

学生做题时不够精细或者模棱两可的时候，往往是定理或者公式把握的不够清晰的情况。教师在演示计算方法，或者计算公式时，如何让学生学到点子上呢？应当强调，并且反复强调。在积累了一定的教学经验后，很容易发现学生掌握不足的知识点。根据实际教学情况，教师讲解这些知识点的时候，就应突出地、反复地强调其中的关键知识点，并适当的辅以助记口诀或者顺口溜，效果会事半功倍。比如，学习复合函数的求导法则——链式法则时，让学生先分析下复合函数的层数，然后引导他们要像“剥洋葱”一样，一层一层地由外而内的求导直至最内层函数。再比如，求解二阶常系数线性非齐次微分方程时，需要构造特解函数，可以告诉学生构造的方法为“右端是什么，就构造什么，然后修正要不要乘x”。经过这样强调，学生解题的思路就清晰多了。

（三）学习和复习相结合，引导学生课外练习

在讲完一大章节的知识点后，学生难免记忆比较零散，不系统，这时安排复习课或者习题课是十分必要的。复习时所讲解的例题可以从学生手头有的课外资料中选取，并且题目的难度稍高于平时讲课的例题，且以综合的或者是发散思维的习题作为补充尤佳。一方面，可以作为章节的结束的标志，和下一章节做一个隔断；另一方面，又可以让学生对手头的资料发生兴趣，积极动手练习。毕竟，数学的学习没有捷径，唯有埋头练习才能提高。

三、教学形式：微创新微突破

（一）借助qq、微信等信息手段，延伸课堂，答疑交流

课堂的时间是有限的，安排答疑也受到时间和空间的限制。而网络是实时的，不受时空间的约束。学生在课外碰到的问题拍个照发到班级qq群、微信群或者直接发给教师，非常便捷。在群里，学生们可以自由讨论，气氛浓烈，越讨论越清晰。即使是学生和教师一对一的问答，在一来一回的交流中，也能让知识在字里行间中传递。

（二）微翻转课堂，增加课堂人文元素

微积分学科的发展，有着无数科学先驱努力和不懈开拓，其间不乏有趣和励志的传奇故事。学生通过查找书籍、文献，阅读这些故事，并在课堂上与学生、老师分享，既了解了一个公式、一个记号背后的故事，又理清了数学发展的历史，并且对数学大家的崇敬也能够激发学生学习的乐趣和动力。这样的微翻转，也是很好的教学形式。

参考文献

［1］苏德矿.高等数学教学如何与中学数学内容及教学方法有效地衔接［J］.中国大学教学，2013（5）：47-49.

中图分类号：G642

文献标志码：A

文章编号：2096-000X（2016）07-0092-02

作者简介：张郑芳（1983-），博士，讲师，从事特征值优化问题的研究。