地面列车动荷载对下穿隧道影响的动力学响应分析
王正安,肖洪天,闫强刚
(1.山东科技大学 土木工程与建筑学院,山东 青岛 266590; 2.青岛市勘察测绘研究院,山东 青岛 266032)
地面列车动荷载对下穿隧道影响的动力学响应分析
王正安1,肖洪天1,闫强刚2
(1.山东科技大学 土木工程与建筑学院,山东 青岛 266590; 2.青岛市勘察测绘研究院,山东 青岛 266032)
摘要:以青岛地铁下穿胶济铁路为研究背景,应用隧道结构的动力有限元数值分析方法,对列车动荷载作用下隧道结构-地层体系的动力响应进行三维数值模拟。分析了单列列车动荷载、两列列车动荷载同向及相向三种工况下,隧道结构-地层体系的应力及位移曲线。研究表明,在列车动荷载作用下,隧道结构-地层体系的动力响应呈现近似简谐波变化;从地表到隧道拱顶的动力响应不断衰减,且衰减速度从地表到隧道拱顶不断减小;两列列车动荷载作用下,隧道结构-地层体系的动力响应值较单列列车动荷载作用下的动力响应值有明显增加,但并未达到单列列车动荷载的两倍。
关键词:列车动荷载;下穿隧道;数值模拟;动力响应;动力分析原理
近年来,城市轨道交通的建设规模不断扩大,由于受原有建筑物的限制和综合利用地下空间的需要,出现了新建地铁隧道下穿既有铁路这种新的形式。隧道结构及地层在上部列车长期反复动力荷载的作用下,隧道结构和周围的软弱地层可能会产生液化或振陷变形,从而危及地铁列车的运行安全。研究列车振动荷载对隧道结构的安全性影响问题成为一个非常重要的课题。张玉娥等[1]在现场试验的基础上,利用频谱分析方法,推导出了地铁列车振动荷载,为分析列车振动荷载作用下地下结构动力响应打下了基础。潘昌实等[2]研究了黄土隧道列车荷载动力响应的有限元数定分析,提出一种人工激振力以模拟列车竖向动荷载。王祥秋等[3]对比分析了列车动荷载作用下不同断面形状振动响应影响的动力响应差异,研究表明:在相同荷载条件下,不同断面形状隧道衬砌结构动力响应规律不尽相同,隧道衬砌结构内力以直墙拱为最大,曲墙拱次之,圆形拱最小。
目前在列车动荷载对隧道结构动力响应的研究方面,主要着重于地铁列车动荷载对本身所在隧道的影响,对研究地面列车动荷载对下穿隧道这一形式的研究较少。本研究以下穿已有铁路的新建隧道为考察对象,利用三维有限元模型,对列车振动荷载作用下隧道结构-地层体系的动力响应进行数值模拟计算。
由于列车从上部经过隧道时产生动荷载,所以在分析列车振动荷载对下部隧道结构的影响,就不能把动荷载简单的作为静荷载处理,必须进行动态分析。本研究以青岛地铁下穿胶济铁路为研究背景,结合隧道结构动力学理论,对列车振动荷载作用下隧道结构及地层动力响应进行三维数值模拟,得到三种工况下的隧道结构-地层体系的动力响应。
1列车振动荷载的模拟方程
由于列车行驶中产生的振动是随机性的,这给列车振动荷载的模拟带来困难。英国铁路技术中心多年来大量理论和实验研究表明,可以用数定法来模拟列车振动荷载[4-5]。产生竖向轮轨力的主要原因有:由轨道接头和焊接造成不平顺;轨枕的间隔排列引起的周期性不平顺;轨枕支撑面的刚实度不同引起的随机性变化以及其他不确定因素。
文献[6]认为,可以用反映不平顺、附加动载和轨面波磨效应的一组激振力来模拟列车振动荷载

(1)
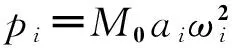
取单边静轮重p0=100 kN,簧下质量M0=750 kg。由于我国高速铁路的运行标准较高,根据《英国不平顺管理值》,取典型不平顺振动波长L1=10 m,L2=2 m,L3=0.5 m;相应的矢高为:a1=3.5 mm,a2=0.4 mm,a3=0.08 mm。取v=80 m/s的列车动荷载曲线,如图1所示:
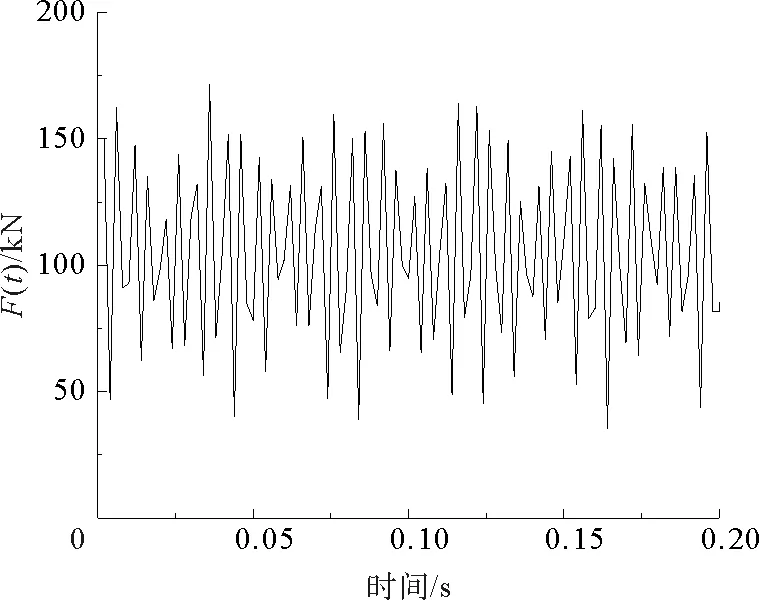
图1 列车动荷载与时间关系图
2隧道结构动力分析原理
2.1数值计算方法
在列车振动荷载作用下,中、低频对隧道结构的动力响应起主要作用,故采用隐式积分法进行分析计算。无条件稳定性是Newmark隐式积分法的特性,故可作为隧道结构动力分析的数值计算方法[7]。
整体体系的运动方程为
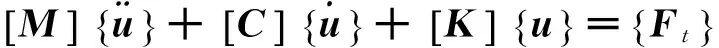
(2a)
隐身积分的特点在于应用t+Δt时刻的平衡条件来求解公式,则体系在t+Δt的动力平衡微分方程为
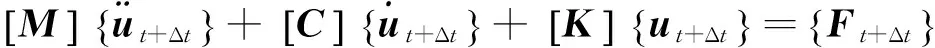
(2b)
根据瑞利法,体系的阻尼矩阵可表示为
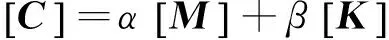
(3)
式中,α=ξω0;β=ξ/ω0,ω0为基频,由对体系进行模态分析确定;ξ为体系相应振型的阻尼比。
Newmark假定在t+Δt时刻有:
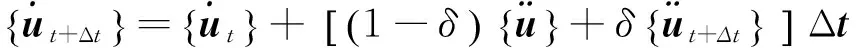
(4)
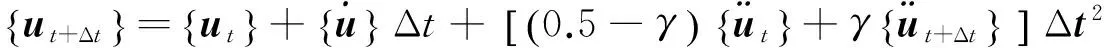
(5)
式中:δ、γ为积分常数;Δt为积分步长,由对体系进行模态分析得到。
2.2动力边界条件
与静力分析不同,动力分析的边界必须要考虑能量的传播。在对隧道结构-地层体系进行动力分析时,列车荷载的振动波能量会在体系中传播,若采用固定边界则会造成能量在边界处聚集,无法传播出去,引起体系的位移变化较大[8]。文献[9-10]提出可以利用黏弹性人工边界模拟半无限空间对能量波的吸收,即在边界上施加线性弹簧和黏性阻尼器。由于本文主要研究列车竖向振动荷载引起的隧道结构-地层体系的竖向应力应变,所以下边界采用黏弹性人工边界模拟半无限域边界,上边界定为自由表面,四周边界定为水平约束。
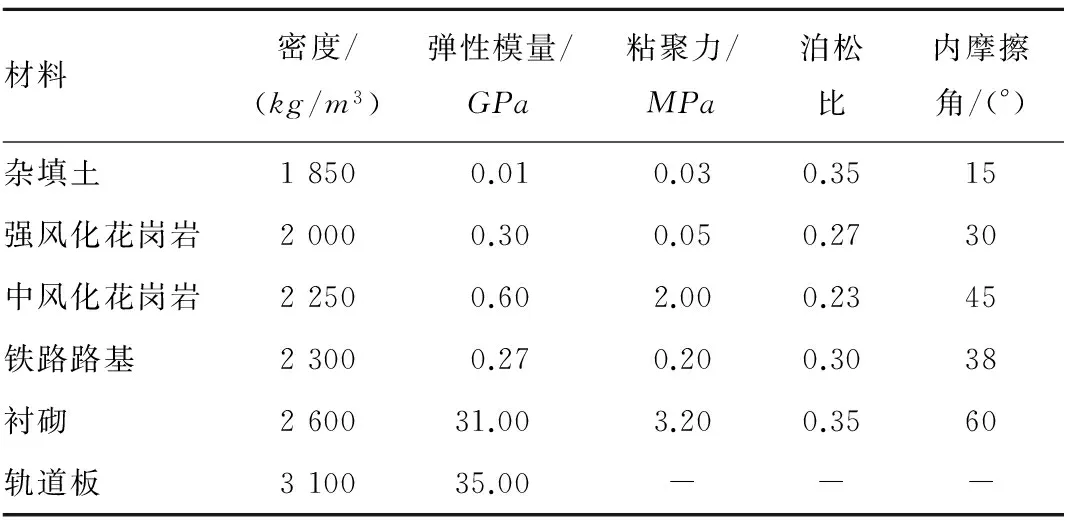
表1 材料物理力学参数
3有限元数值模拟
3.1工程地质概况
青岛地铁一期工程3号线隧道顶埋深约6.0~20.0m,隧道所处位置岩体主要是中风化花岗岩,构造节理及风化裂隙较发育,多为高角度节理。岩体完整性指数为0.3~0.5,属较破碎的较软岩,岩体基本质量等级Ⅳ级。根据研究重点,暂不考虑岩体中节理裂隙的影响,根据勘察报告和铁路隧道设计规范要求,确定各种材料物理力学参数如表1所示。
3.2计算模型
为全面反映列车动荷载作用下隧道结构及地层的动力学响应,取地铁隧道尺寸6.5m×6.2m,隧道横向取160m,竖直方向取30m,延伸方向取60m。结合表1中各材料的物理力学参数,利用ANSYS有限元数值模拟软件得到的计算模型如图2所示。
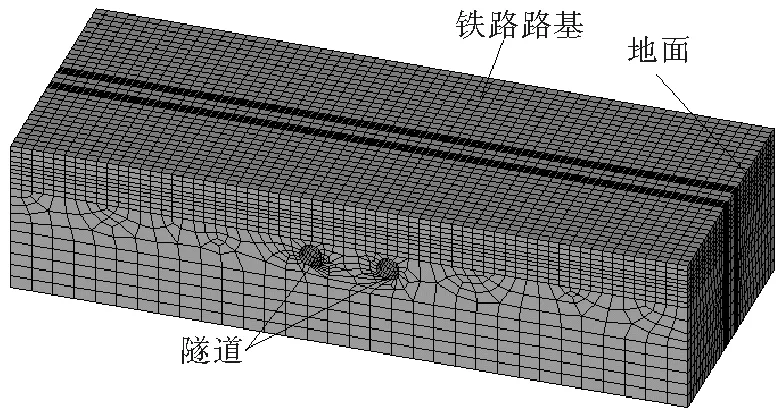
图2 分析模型的有限元网格
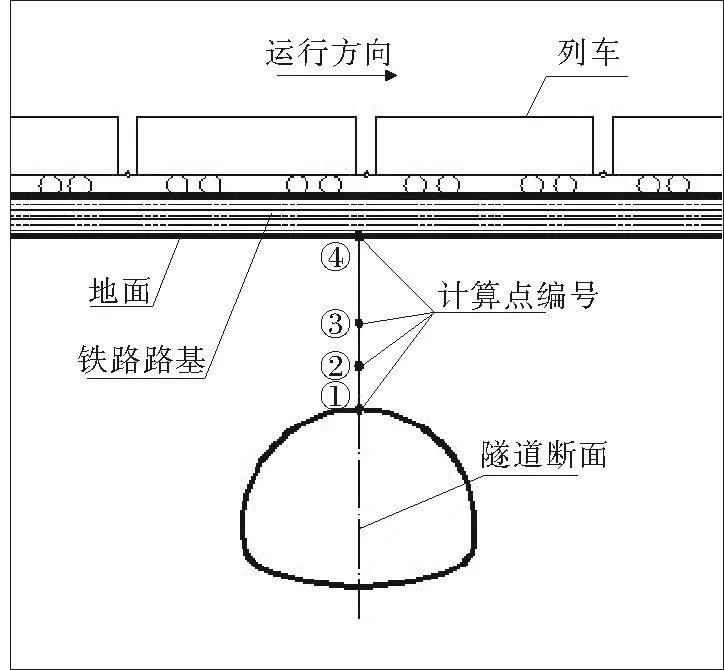
图3 计算点分布图
4动力计算及结果分析
针对青岛地铁下穿胶济铁路的情况,为了更真实地反映列车振动荷载作用的下穿隧道动力响应,模拟在相同速度下,单辆列车动荷载作用下(工况一)、同向行驶的两辆列车动荷载作用下(工况二)、相向行驶的两辆列车动荷载作用下(工况三)隧道结构的动力响应。
同时为研究列车动荷载作用下地层不同深度的动力响应,在地下不同深度和隧道拱顶布置计算点(图3),并以左侧隧道为主要研究对象。
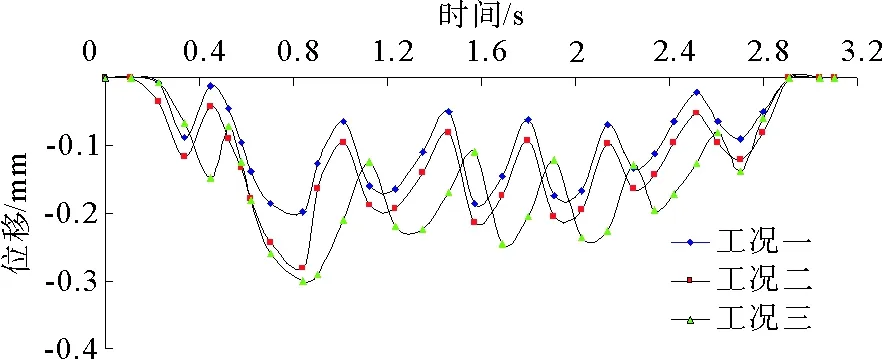
图4 三种工况下的拱顶位移时程曲线
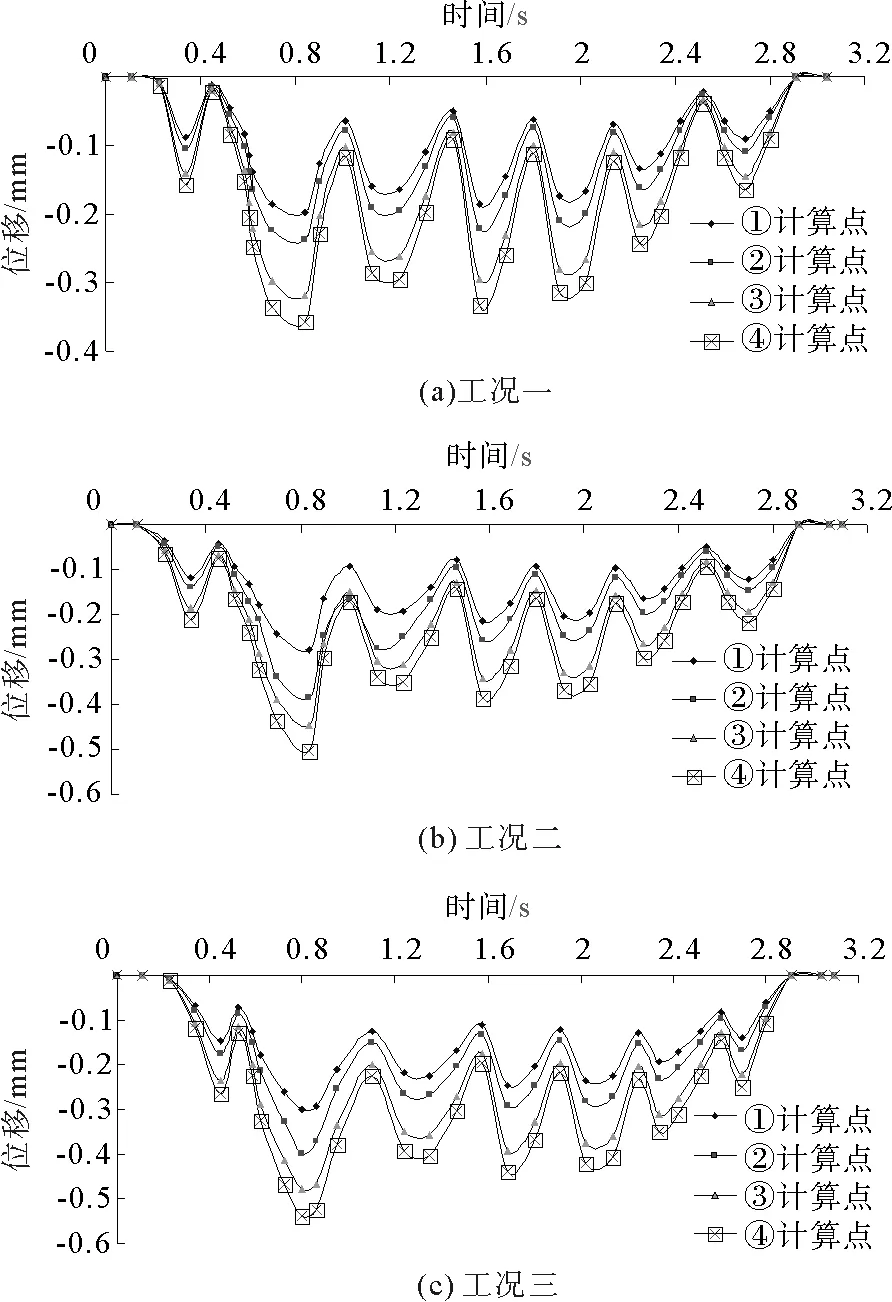
图5 各计算点位移时程曲线
4.1隧道拱顶计算点位移分析
模拟计算时间从列车进入模型边界开始,以列车完全离开模型边界结束。利用ANSYS数值模拟软件对模型进行瞬态动力学分析,得到三种工况下隧道拱顶计算点位移时程曲线,如图4所示。
通过图4对比三种工况下的拱顶位移时程曲线可知:
1)随着列车逼近隧道上方,隧道拱顶位移量逐渐增大;当列车经过隧道正上方时,位移达到峰值,随后隧道结构呈现出如图4所示的近似简谐波式的动力响应并逐渐衰减到0。
2)列车动荷载作用下,与隧道开挖引起的最大沉降量(12mm)相比,隧道拱顶位移变化量很小(三种工况下的最大位移为0.3mm),几乎可以忽略不计。但是由于隧道上方的胶济铁路是重要的铁路运输线,列车频繁通过,在列车振动荷载的长期作用下,隧道结构及软弱地层可能会产生液化或振陷变形,从而威胁铁路运行安全,所以不能忽视列车动荷载产生的沉降量。
3)对比三种工况下的拱顶计算点位移曲线可知,三种工况下的位移变化规律大致相同。工况三和工况二相比,位移有所增加但增加幅度不大。工况二和工况三与工况一相比,拱顶下沉量显著增加,但并未达到工况一的两倍,说明列车振动荷载对下穿隧道的影响具有累积叠加效应,但并不是成倍叠加的。
4.2地层不同深度位移分析
列车动荷载在不同深度地层的动力响应是不同的,为了得到列车振动荷载作用下不同深度地层的位移变化规律,在地层不同深度设置计算点(图3)并记录各点位移变化,得到三种工况下的不同深度地层的位移时程曲线(图5)和各计算点最大位移值(表2)。
对比分析三种工况下地层不同深度计算点的位移时程曲线和最大位移值,可知:
1)与拱顶位移变化规律相似,地层不同深度计算点的位移也呈近似简谐波式的变化,并最终衰减到0。
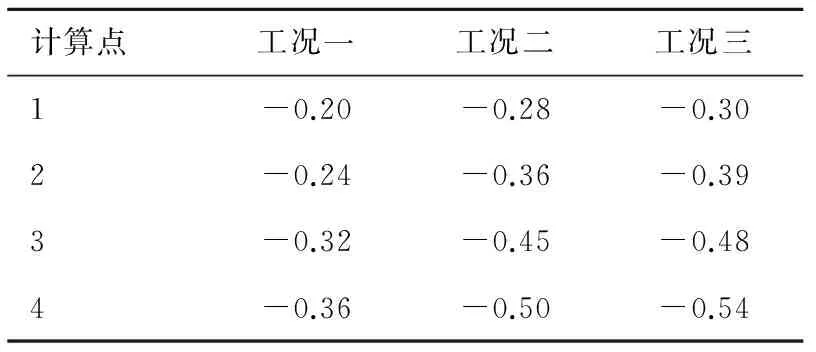
表2 三种工况下不同深度计算点的最大位移值
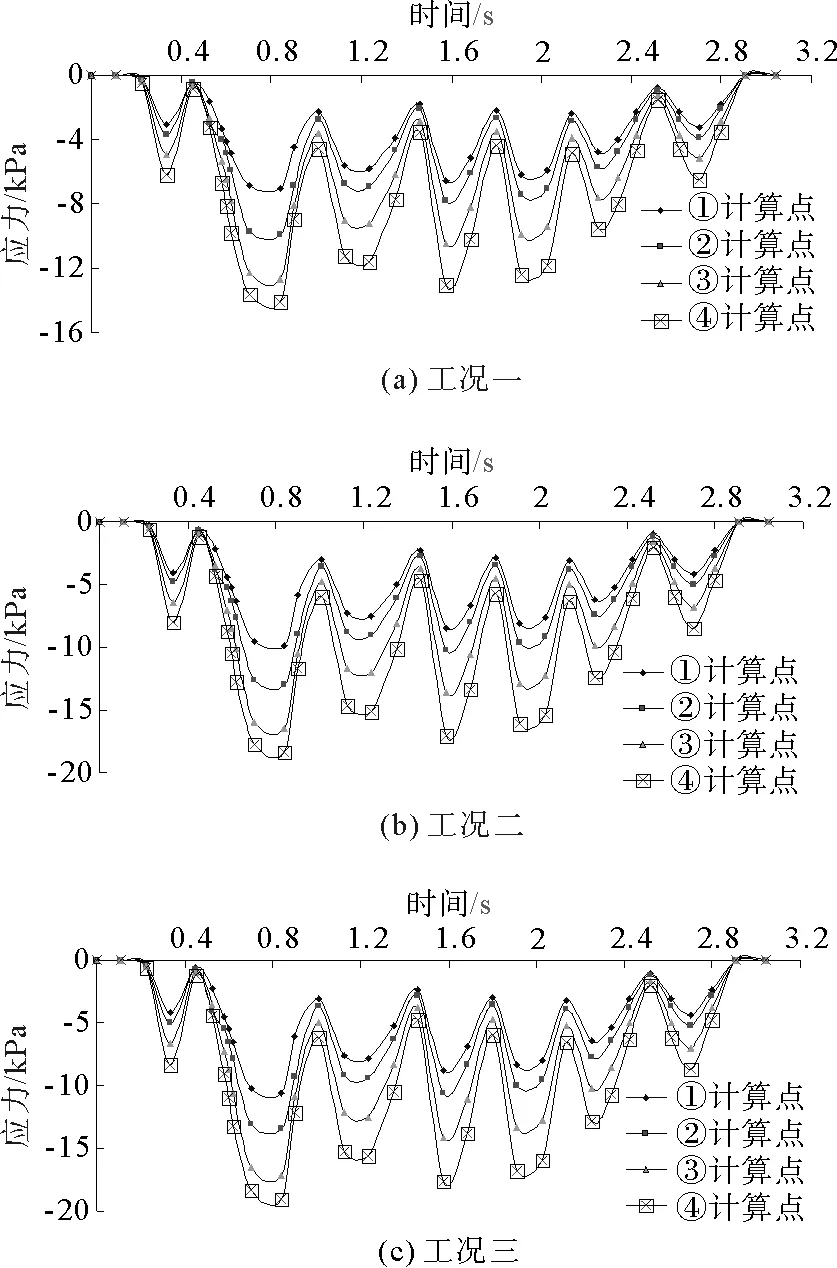
图6 各计算点应力时程曲线
计算点工况一工况二工况三1-7.04-9.86-10.562-9.51-12.94-13.443-12.68-16.48-17.114-14.09-18.31-19.02
2)对比三种工况下各计算点位移时程曲线可知,地层各计算点的位移从地表到拱顶均是逐渐减小的。说明随着地层深度的增加,列车振动波能量不断衰减,使得深地层的动力响应减小。
3)对比表2中各计算点的最大位移可知,成倍列车动荷载的叠加并不能引起地层不同深度位移成倍增加。
4.3地层不同深度应力分析
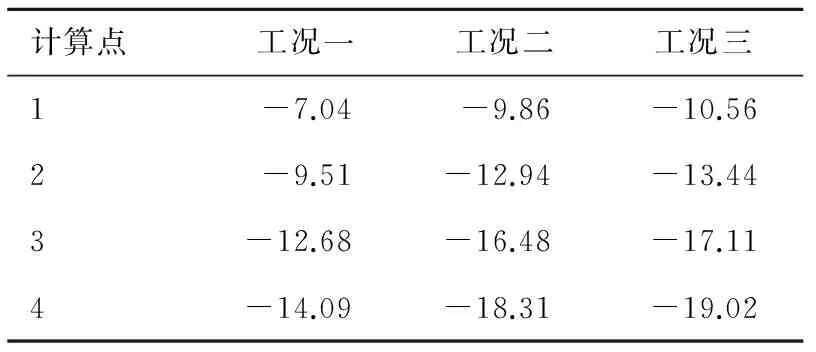
为了得到列车振动荷载作用下不同深度地层的应力变化规律,在地层不同深度相同位置设置计算点(图3)并记录各点应力变化,得到三种工况下的不同深度地层的应力时程曲线(图6)和各计算点最大应力值(表3)。
三种工况下,地层不同深度计算点位移、应力最大值分别如表2和表3所示。对比三种工况下地层不同深度计算点的应力情况可知,各计算点应力变化表现出近似相同特性:
1)三种工况下,列车振动荷载作用下,地层不同深度计算点的应力均是在列车经过正上方时达到最大值,然后做近似简谐波变化。
2)三种工况下,地层各计算点的应力从地表到拱顶均是逐渐减小。说明随着地层深度的增加,由于地层阻尼等因素影响,列车振动波能量不断衰减,使得深地层的动力响应减小。
3)三种工况下,地层不同深度各计算点的应力衰减速度均是从地表到拱顶逐渐减小,但是可能受隧道拱顶的压力拱效应影响,在隧道拱顶附近的衰减速度较快。
通过与现场监测数据对比分析发现,上述结论与现场实际监测情况基本吻合,验证了模拟分析的正确性。
5结论
结合青岛地铁下穿胶济铁路的实例,通过引入激振力实现了对列车振动荷载的模拟,结合隧道结构的动力分析原理,利用有限元软件模拟列车动荷载作用下隧道结构及地层的动力响应,结论如下:
1)隧道结构及地层在列车动荷载作用下,呈现出近似简谐波的动力响应并最终衰减到0。
2)两列同向列车动荷载作用下隧道结构及地层的动力响应和相向列车动荷载相比,有所增加但增加幅度不大。两列列车动荷载下隧道结构及地层的动力响应与单列列车动荷载相比,有显著增加,但由于地层阻尼等因素影响,并未达到单列动荷载作用下动力响应的两倍。
3)单列或双列列车动荷载作用下,地层的动力响应从地表到隧道拱顶逐渐衰减,而且衰减速度也是从地表到拱顶逐渐减小的。
参考文献:
[1]张玉娥,白宝鸿.地铁列车振动对隧道结构激振荷载的模拟[J].振动与冲击,2000,19(3):69-70.
ZHANGYu′e,BAIBaohong.Themethodofidentifyingtrainvibrationloadactingonsubwaytunnelstructure[J].JournalofVibrationandShock,2000,19(3):69-70.
[2]潘昌实,PANGN.黄土隧道列车动荷载响应有限元初步数定分析研究[J].土木工程学报,1984,17(4):18-28.
PANChangshi,PANGN.Preliminarydeterministicfiniteelementstudyonatunneldriveninloesssubjectedtotrainloading[J].ChinaCivilEngineeringJournal,1989,17(4):18-28.
[3]王祥秋,杨林德,周治国.列车振动荷载作用下隧道衬砌结构动力响应特性分析[J].岩石力学与工程学报,2006,25(7):1337-1342.
WANGXiangqiu,YANGLinde,ZHOUZhiguo.Dynamicresponseanalysisofliningstructuresfortunnelundervibrationloadsoftrain[J].ChineseJournalofRockMechanicsandEngineering,2006,25(7):1337-1342.
[4]李亮,张丙强,杨小礼.高速列车振动荷载下大断面隧道结构动力响应分析[J].岩石力学与工程学报,2005,24(13):4260-4263.
LILiang,ZHANGBingqiang,YANGXiaoli.Analysisofdynamicresponseoflargecross-sectiontunnelundervibratingloadinducedbyhighspeedtrain[J].ChineseJournalofRockMechanicsandEngineering,2005,24(13):4260-4263.
[5]梁波,罗红,孙常新.高速铁路振动荷载的模拟研究[J].铁道学报,2006,28(4):89-94.
LIANGBo,LUOHong,SUNChangxin.Simulatedstudyonvibrationloadofhighspeedrailway[J].JournaloftheChinaRailwaySociety,2006,28(4):89-94.
[6]梁波,蔡英.不平顺条件下高速铁路路基的动力分析[J].铁道学报,1999,21(2):85-87.
LIANGBo,CAIYing.Dynamicanalysisonsubgradeofhighspeedrailwayingeometricirregularcondition[J].JournaloftheChinaRailwaySociety,1999,21(2):85-87.
[7]于鹤然,周晓军.高速列车动荷载作用下立体交叉铁路隧道动力响应研究[J].铁道学报,2015,37(6):104-110.
YUHeran,ZHOUXiaojun.Studyondynamicresponseofgrade-separatedrailwaytunnelsunderhigh-speedtraininduceddynamicload[J].JournaloftheChinaRailwaySociety,2015,37(6):104-110.
[8]白冰,李春峰.地铁列车振动作用下近距离平行隧道的弹塑性动力响应[J].岩土力学,2009,30(1):124-127.
BAIBing,LIChunfeng.Elastoplasticdynamicresponsesofcloseparallelmetrotunnelstovibrationloading[J].RockandSoilMechanics,2009,30(1):124-127.
[9]高玄涛.高速铁路列车振动荷载对下穿隧道地层动力响应分析[J].铁路标准设计,2014,58(6):93-96.
GAOXuantao.Analysisonstratumdynamicresponsetotrainvibrationloadwhentunnelingbelowanexistinghigh-speedrailway[J].RailwayStandardDesign,2014,58(6):93-96.
[10]王启云,张家生,孟飞,等.高速铁路路基模型列车振动荷载模拟[J].振动与冲击,2013,32(6):43-46.
WANGQiyun,ZHANGJiasheng,MENGFei,etal.Simulationoftrainvibrationloadonthesubgradetestingmodelofhigh-speedrailway[J].JournalofVibrationandShock,2013,32(6):43-46.
(责任编辑:吕海亮)
Analysis of Dynamic Response of Undercrossing Tunnels to Vibration Loads of Ground Trains
WANG Zheng′an1,XIAO Hongtian1,YAN Qianggang2
(1.College of Civil Engineering & Architecture, Shandong University of Science and Technology,Qingdao,Shandong 266590,China;2.Qingdao Institute of Surveying and Mapping,Qingdao,Shandong 266032,China)
Abstract:With Qingdao tunnels below Qingdao-Jinan high-speed railway as the research background, a three-dimensional numerical simulation was conducted on the dynamic response of the tunnel-stratum system to vibration loads of train by using dynamic finite element method of tunnel structures. The vertical displacements and stress of the tunnel-stratum system were analyzed under the vibration load of one train, under the vibration of two trains in the same direction and under the vibration of two trains in the opposite directions. Results show that the dynamic response curves of tunnel-stratum system under vibration load of train are approximate harmonic waves. The dynamic response of stratum decays continually and the decay rate is decreases from the surface to the arch crown of the tunnel. The dynamic response of the system under the action of loading induced by two trains is significantly increased compared with that induced by one train. However, the maximum dynamic response induced by two trains has not reached two times as much as that induced by one train.
Key words:vibration loads of train;tunneling below existing structure;numerical simulation;dynamic response;dynamic analysis principle
收稿日期:2015-10-28
基金项目:青岛市建设科技计划项目(JK2014-9)
作者简介:王正安(1989—),男,山东枣庄人,硕士研究生,主要从事地下工程稳定性研究. 肖洪天(1964—),男,河北沧州人,教授,博士,博士生导师,主要从事岩石力学数值方法研究,本文通信作者. E-mail:xiaohongtian@tsinghua.org.cn
中图分类号:U45
文献标志码:A
文章编号:1672-3767(2016)03-0067-06

