纳米压印技术脱模过程机理分析
马立俊,王 清,张 睿,张金涛,郑 旭
(山东科技大学 土木工程与建筑学院,山东 青岛 266590)
纳米压印技术脱模过程机理分析
马立俊,王清,张睿,张金涛,郑旭
(山东科技大学 土木工程与建筑学院,山东 青岛 266590)
摘要:为了减少脱模导致的产品缺陷,对纳米压印技术中的脱模机理进行研究。基于界面力学的接触理论提出了模板和聚合物之间作用力的理论模型,利用ANSYS软件模拟模板和聚合物的接触分离过程。采用断裂力学能量平衡理论,通过脱模力和脱模位移之间的关系分析脱模规律和机理。研究结果表明,脱模过程中不同位置接触面上的作用力存在较大差异;高宽比为2和1.5时,脱模力曲线有两个峰值,高宽比为1和0.5时,脱模力曲线有一个峰值;残余层厚度增加,与同一脱模力相对应的脱模位移会相应增大,但不影响最大脱模力的数值。
关键词:脱模过程;机理;接触;黏结力;脱模力;脱模位移
纳米压印技术[1](nano-imprint lithography,NIL)是目前国际上普遍关注的一种全新的微纳米结构制造技术,因其有低成本、高效率等优点而被看作是最具有工业化应用前景的微纳米结构制造方法之一。由于该技术采用宏观技术手法对物体微观领域进行改造,很难避免产品制造过程中出现的缺陷问题。
为了降低产品缺陷率,提高产品精度,国内外学者对纳米压印技术做了大量的研究。从工艺流程的角度出发,产品缺陷的产生发生在压印过程及脱模过程中。针对压印过程中产生缺陷的研究较多,如何提高模板空腔中聚合物的填充率成为这类研究的重点。Ryu等[2]研究了加压过程中不同的压力变化率对聚合物填充效率的影响;Taylor等[3]研究了在热塑性压印中模板空腔中的滞留气体对填充效率的不利影响;贺永等[4]利用Deform-2D对微热压成型过程进行有限元模拟,研究了模具结构对聚合物流动形貌的影响;Kim等[5]对热压印技术压印过程中黏性聚合物的流动性填充表现进行研究。针对脱模过程中产生缺陷的研究相对较少。其中,王清等[6]研究了脱模过程中模板和聚合物成型体之间的接触力变化;汤启升等[7]提出卷对卷纳米压印脱模的两种形式,并采用有限元模拟的方法分析了脱模过程中的阻力;Song等[8]通过有限元分析,研究了热压印技术中聚合物的压力和变形对脱模的影响。国内外众多学者所做的工作极大地推动了纳米压印技术的发展和实际应用,并为未来的研究指明了方向。
纳米压印技术中脱模规律和机理的研究对于减少脱模过程中产生的缺陷有着重要意义。然而,目前的研究模型忽略了不同位置接触面上作用力存在的差异,而且研究主要针对模型结构以及参数的优化,对模板和聚合物之间的接触分离状态反映不全面,脱模规律和机理的研究有待深入。本文根据界面力学中的DMT理论[9],提出了适用于纳米压印技术脱模过程的理论模型,并得出不同位置接触面上相互作用力的差异分布;依据理论模型以及接触面上作用力分布特点,利用ANSYS 15.0有限元分析软件,以热压印脱模过程为例,对其进行数值模拟;采用断裂力学中的能量平衡理论对模拟出的脱模力与脱模位移之间的关系进行分析;最后,研究了模板凸起结构高宽比以及残余层厚度对脱模的影响。
1理论模型与数值模拟
1.1接触力理论模型
纳米压印技术中的脱模过程在本质上是克服模板和聚合物之间的接触力,其中,接触力主要包括黏结力和摩擦力。黏结力在模板和聚合物横向接触面之间未完全分离或竖向接触面之间还未出现相对滑动时起阻碍脱模作用,这时的黏结力也称为初始黏结力;摩擦力在竖向接触面之间出现相对滑动时起阻碍脱模作用。脱模时,首先破坏模板和聚合物接触之间的黏结力,其次克服模板与聚合物竖向接触之间的摩擦力,并保持聚合物和模板结构完整性的情况下完成两者分离。
传统的接触理论考虑的是两个物体在外力作用下的相互接触,没有考虑两者之间表面力的作用,但是,当研究对象的特征尺度减小到一定范围时,将出现很多传统宏观接触理论所无法解释的现象。如零外载下接触面的塑性屈服,接触过程中的突跳,两个接触面的黏着现象等[10]。表面能和由其派生的表面力是决定固体表面黏着、接触、变形等行为的关键因素。由于纳米压印技术已经接近微观尺度,所以表面原子或分子之间的相互作用是必须要考虑的。
在脱模时,聚合物已经固化成型。考虑表面原子或分子之间的相互作用,两固体互相接触而构成界面后,其Dupré黏着能为[11]
Δγ=γ1+γ2-γ12。
(1)
式中,γ1和γ2分别为两固体表面的自由能;γ12为界面能。
模板和聚合物之间的黏结力可用Pollock方程[12]计算
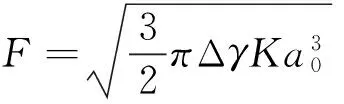
(2)
式中,Δγ为两材料间的黏着能;K为两材料的当量弹性模量;a0为有效接触半径。
当量弹性模量可由下式求出
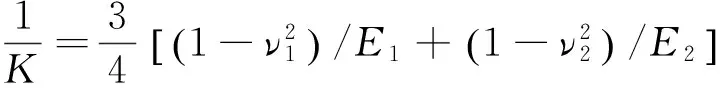
(3)
式中,E1、E2和ν1、ν2分别为两材料的弹性模量和泊松比。
模板和聚合物竖向接触之间的摩擦力可由下式计算[13]
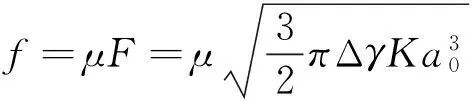
(4)
式中,μ为摩擦系数;F为黏结力。
由公式(2)可知,黏结力不仅与材料属性有关,而且与接触面的有效接触半径有关;由公式(4)可知,摩擦力与黏结力有关,这里的黏结力与初始黏结力略有不同,是由于两种不同材料在竖向接触面上出现相对滑动时产生的。
根据界面力学中的赫兹弹性接触理论[9],两个物体相接触时,在载荷作用下接触附近的材料将发生形变,从而形成一个有限的区域接触,这区域远小于物体的宏观尺寸,因而几何上和弹性参数上都可以做适当的简化。将模板和聚合物之间的接触看作是两个弹性固体球面之间的接触,设两球的半径分别为R1和R2,在载荷W的作用下,由赫兹接触理论得到接触区的半径a满足
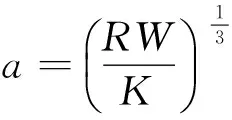
(5)
但在实际的观测中发现在外载较小时,物体之间的接触面积远大于利用赫兹接触理论预测的结果,并且在载荷逐渐减小到零时接触面积区域保持恒定。这表明在固体之间有表面吸引的相互作用[9]。
Derjaguin、Muller和Toprov给出了考虑表面接触黏着力时修正的赫兹关系[14]
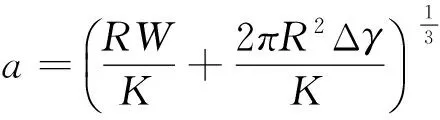
(6)
式(6)一般被称为DMT理论。根据修正的赫兹理论模型,可知在压印力逐渐减小到0时,有效接触半径会降低为一个常数,但是对于压印模型这种特殊结构来说,模板和聚合物竖向接触之间的黏结力和摩擦力会在很大程度上抑制由于压印力消失而造成的有效接触半径的减小。压印力W在聚合物处于熔融状态时施加到模板上,待聚合物固化后逐渐降为零。考虑到纳米结构表面的粗糙度,聚合物由流体固化成固体的过程中,与模板接触面上的黏结力以及摩擦力会有所增加,这进一步抑制了有效接触半径的减小。由于以上原因,计算脱模时黏结力所需的有效接触半径可取压印力存在状态下、由修正的赫兹模型计算出的有效接触半径。
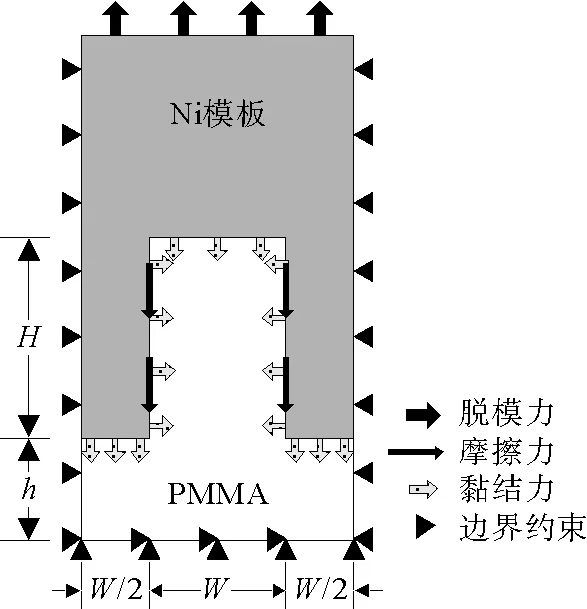
图1 脱模过程中作用力分布与几何模型、边界条件
图1展示了纳米压印技术脱模过程中作用力的分布情况。在实际压印过程中,模板凸起底部与残余层最先接触,模板凸起底部接触面属于直接施压面,与其相接触的残余层接触面属于直接承压面,所以这部分接触面上的压力最大。填充到模板空腔中的聚合物与模板凸起侧壁之间的压力较小,而模板空腔顶部与聚合物横向接触的压力需要通过填充接触的状态来确定。根据理论模型并结合实际压印过程可以得出脱模时底部横向接触面的黏结力最大,而侧壁竖向和顶部横向接触面上的黏结力较小。
1.2脱模过程数值模拟
基于上述理论模型利用ANSYS 15.0建立数值仿真模型。为了避免压印过程中出现的聚合物不完全填充对脱模结果造成的影响,采用处于完全填充状态的压印模型对脱模过程进行模拟。选用镍(Ni)作为模板材料,聚甲基丙烯酸甲酯(polymethylmethacrylate,PMMA)作为胶层材料,并选用Mooney-Rivlin模型模拟PMMA材料的力学性能[15],建立2D有限元模型模拟模板与聚合物之间的分离过程。两种材料的基本属性见表1。为了符合理论模型,本文采用ANSYS新增的Debonding功能来模拟模板和聚合物底部以及顶部横向接触之间的分离,考虑到模板和聚合物竖向接触分离过程中既有黏结力的作用,又有摩擦力的作用,采用建立接触对的方式来模拟其分离。几何模型和边界条件如图1所示。

表1 模板和胶层的材料属性
2分析与讨论
2.1脱模过程机理分析
对聚合物凸起宽度W=200 nm、高度H=400 nm、残余层厚度h=200 nm的压印模型进行脱模模拟,得出脱模力与脱模位移之间的关系,以及不同脱模阶段的模板与聚合物位移云图,如图2及图3所示。根据图2脱模力与脱模位移之间的关系将整个脱模过程分为五个阶段,采用断裂力学中的能量平衡理论[16],并结合位移云图3对不同脱模阶段进行分析。
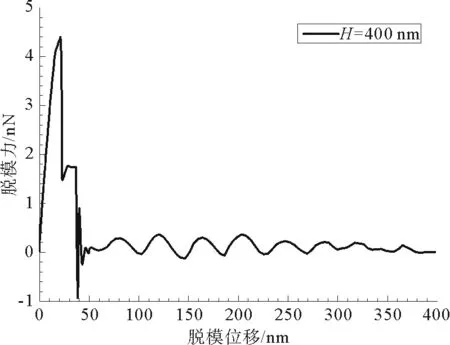
图2 脱模过程中脱模力与位移之间的关系
第一阶段是残余层弹性变形阶段,变形方向平行于位移方向。随着脱模位移的增加,脱模力从0开始逐渐增大。在这阶段内,模板和聚合物各部分接触之间还处于完全接触状态,没有产生初始裂纹,考虑到残余层是一种弹性材料,脱模力和位移之间呈线性关系。由于模板和聚合物的弹性模量相差很大,所以这一阶段的脱模位移是由于脱模力对残余层做功所引起的弹性变形导致的位移。对于填充到模板空腔中的聚合物来说,模板和聚合物的竖向接触面存在黏结力和摩擦力,这就使得和模板侧壁接触的聚合物出现和模板相同的脱模位移。如图3(a)所示,由于聚合物的弹性模量较小,聚合物凸起的中间部分与模板侧壁相接触的两边部分会出现相对位移,导致聚合物凸起中间部分产生的向上位移小于凸起两侧部分产生的向上位移,所以聚合物凸起中间部分的弹性变形对于脱模位移也有较小贡献。当脱模位移达到21 nm时,脱模力达到最大值4.4 nN,模板凸起底部和残余层横向接触即将分离,如图3(b)所示。此时,残余层的弹性变形和拉伸应力达到最大值,单位体积内储存的应变能达到最大值。

图3 不同脱模阶段的位移云图
第二阶段是模板凸起底部和残余层横向接触分离阶段,裂纹的扩展方向垂直于位移方向。当残余层储存的应变能超过底部横向接触处产生裂纹所需能量的临界值时,便产生初始裂纹。由于初始裂纹表面应力消失,释放出部分弹性应变能,被释放的弹性应变能克服了模板和聚合物接触阻力所做的功,即应变能释放率大于模板和聚合物接触分离时产生新表面吸收的能量率,则裂纹失稳,继续扩展。裂纹的扩展伴随着应变能释放和新表面产生所需能量吸收,在应变能释放率大于吸收的能量率情况下,无需持续增加荷载来延续裂纹的扩展。裂纹持续扩展直到模板凸起底部与残余层完全分离,残余层形变势能恢复到最初的状态。裂纹的扩展方向是横向的,模板的位移方向是竖向的,裂纹的横向扩展无助于模板位移的增加,正如图2所示,脱模力从最大值下降到较小值时,脱模位移并没有发生变化。
第三阶段是模板和聚合物竖向接触黏结力失效阶段,裂纹的扩展方向平行于位移方向。底部横向接触完成分离后,模板和聚合物竖向接触上的黏结力开始起作用。在这一阶段,模板顶部均匀施加的脱模力先是对填充到模板空腔中的聚合物凸起底部做功,使其产生弹性形变。当侧壁底部的部分聚合物储存的应变能达到侧壁底部接触边界上产生裂纹所需能量的临界值时,侧壁的底部接触面产生裂纹。在应变能释放率大于侧壁接触分离时产生新表面吸收的能量率情况下,裂纹沿着侧壁向上扩展,裂纹的扩展伴随着变形的恢复、能量的释放。随着裂纹的扩展,聚合物储存的应变能减少,当减少到应变能释放率小于产生新表面吸收的能量率时,裂纹向上扩展的趋势减缓,持续的脱模力便开始对裂纹尖端以上的部分聚合物做功,使其产生弹性形变,储存形变势能,然后继续扩展,就这样裂纹持续扩展,直至侧壁裂纹贯通。事实上,聚合物凸起的变形在一定程度上会使其出现颈缩现象,这一现象加剧了竖向接触黏结力的失效,使得侧壁裂纹的扩展和贯通更加迅速。
第四阶段是模板空腔顶部和聚合物凸起顶部横向接触分离阶段,裂纹的扩展方向垂直于位移方向。在竖向接触上的黏结力失效、裂纹贯通后,顶部横向接触开始阻碍脱模的进行。顶部横向接触的分离过程与底部横向接触的分离过程是相似的,且顶部横向接触面的黏结力小于底部横向接触面的黏结力,这使得顶部横向接触之间的分离较容易。这一阶段的脱模力主要作用于顶部横向接触处,随着脱模力的增加,聚合物凸起产生变形,使得脱模位移增大,聚合物凸起储存的应变能增大,如图3(c)所示。当聚合物凸起储存的应变能达到顶部横向接触处产生裂纹所需能量的临界值时,便产生了初始裂纹。由于初始裂纹表面应力消失而释放出部分弹性应变能,被释放的弹性应变能克服了模板和聚合物接触阻力所做的功,则裂纹失稳,持续扩展,直到顶部横向接触完全分离。在聚合物凸起的弹性形变恢复到平衡状态时,会由于惯性作用超过平衡状态,导致凸起出现向下的位移,如图3(d)所示,使得聚合物凸起出现瞬间增粗现象。这一现象在恢复为平衡状态之前,会使得模板产生负的脱模力,如图2脱模位移在39 nm时所示。裂纹的扩展方向垂直于模板的位移方向,裂纹的横向扩展无助于模板位移的增加,脱模力在第二次大幅度下降时,脱模位移并没有发生变化,如图2所示。
第五阶段是模板和聚合物竖向接触处产生相对位移,摩擦力开始起作用,直至聚合物凸起脱离模板空腔,完成分离。随着顶部横向接触的分离,模板和聚合物所有接触面上的黏结力全部失效,聚合物凸起脱离模板空腔的过程是脱模力克服模板和聚合物竖向接触之间摩擦力的过程。由于模板和聚合物的弹性模量相差很大,使得它们竖向接触之间产生的摩擦力和两个弹性模量较大且相接近的物体接触之间产生的摩擦力略有不同,脱模力在克服摩擦力使模板产生脱模位移时,会使得聚合物凸起产生相对于模板凸起而言较大的变形。聚合物凸起变形增加,脱模位移和脱模力增大,形变势能也相应增加,当势能增加到一定程度,侧壁上的竖向接触由静止状态变为滑动状态,聚合物凸起产生相对于模板凸起向下的位移,恢复变形,释放势能。此时,聚合物凸起的形变势能降低,侧壁上的竖向接触由滑动状态又转换为静止状态,脱模力再次对聚合物凸起做功,增加形变势能。脱模力克服竖向接触上的摩擦力产生脱模位移的过程是一种能量不断积累和释放的循环过程,如图2所示,脱模位移超过100 nm以后,曲线展示出不断波动的状态。在摩擦力开始起作用的第一个能量循环过程中,此时的竖向接触面积是最大的,由静止状态转换为滑动状态的势能临界值也是最大的。在随后的能量循环过程中,竖向接触面积与势能临界值逐渐减小,这正是图2展示的曲线波动不断变小的原因。当脱模位移达到400 nm时,脱模力降为0,聚合物凸起完全脱离模板空腔,完成整个脱模过程。
2.2聚合物凸起高宽比对脱模力的影响
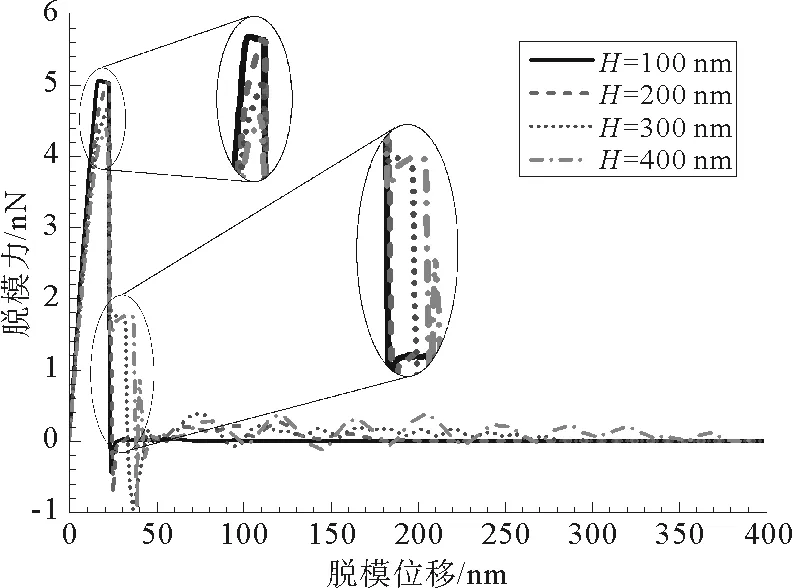
图4 脱模力随凸起高度H变化曲线
通过以上对聚合物凸起高宽比较大的压印模型进行脱模机理分析,可以看出不同位置接触之间黏结力的失效过程是有一定顺序的,然而针对高宽比较小的压印模型进行脱模时,却出现了不同的规律。图4展示了残余层厚度h为200 nm,聚合物凸起宽度W=200 nm,高度H分别为100、200、300和400 nm的脱模力与位移之间关系曲线。由图中可以看出,在纳米结构高宽比小于等于2时,脱模位移在50 nm范围内,高宽比H/W为2和1.5的压印模型,脱模力出现了两个极大值;高宽比为1和0.5的压印模型,脱模力出现了一个极大值;出现一个极大值时的脱模力最大值略大于出现两个极大值时的脱模力最大值。高宽比增大,底部和顶部横向接触面积不变,竖向接触面积增加,这使竖向接触黏结力失效及摩擦力起作用时相对应的脱模阶段所需的脱模力增大。结合脱模机理分析可知,摩擦力起作用的阶段对应的是第五阶段,该阶段脱模力增加对最大脱模力没有贡献,而对于竖向接触黏结力失效阶段增加的脱模力会使最大脱模力增加。根据脱模机理分析,接触上的黏结力是按照从底部横向接触、竖向接触、顶部横向接触这一顺序失效的,且横向接触分离时对应的脱模力是脱模力极大值。高宽比越大,这一顺序表现越明显,底部和顶部横向接触先后分离的间隔越长,就出现两个脱模力峰值;高宽比越小,顺序性越不明显,底部和顶部横向接触的分离就会有叠加,当高宽比小于1时,脱模力就叠加成一个峰值。底部和顶部横向接触分离时的叠加效应使脱模力峰值增加,即最大脱模力增加。高宽比小于等于2时,由于高宽比减小而引起的脱模力叠加效应所导致的脱模力增加值略大于由于高宽比增大而引起的竖向接触面积增加所导致的最大脱模力增加值。
2.3残余层厚度对脱模位移的影响
为了进一步研究聚合物残余层厚度对脱模力与脱模位移的影响,选取聚合物凸起宽度W=200 nm,高度H=100 nm,残余层厚度h分别为200、500 nm,以及聚合物凸起宽度W=200 nm,高度H=200 nm,残余层厚度h分别为200、400 nm为研究对象,作出相应的脱模力与脱模位移关系曲线图,如图5所示。由图5(a)和(b)可以看出,残余层厚度主要对脱模过程中与同一脱模力相对应的脱模位移产生影响,对最大脱模力的值无影响。在脱模过程中,聚合物凸起相同,残余层厚度越大,与同一脱模力相对应的脱模位移越大,最大脱模力出现时所对应的脱模位移也越大。
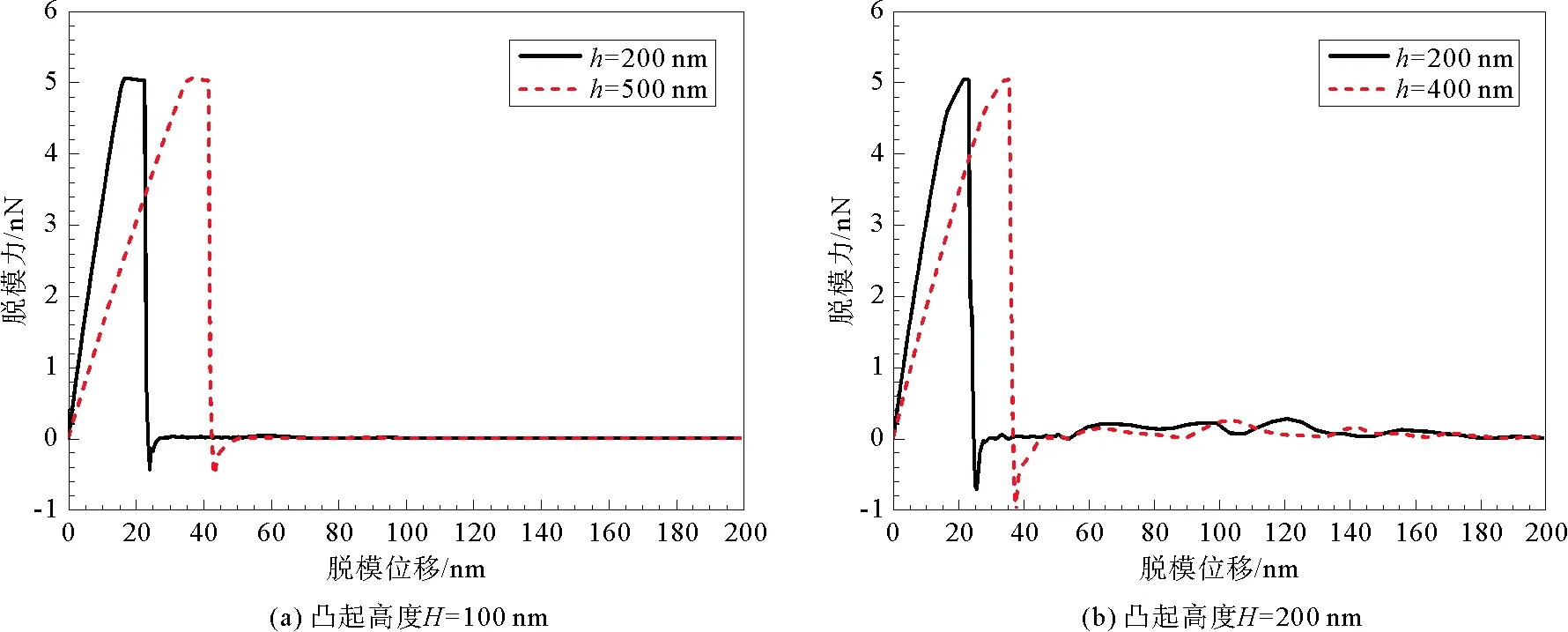
图5 脱模力随残余层厚度h变化曲线
3结论
1)根据界面力学中的DMT理论,并结合小特征尺度固体接触的表面效应影响,提出了适用于纳米压印技术脱模过程的作用力理论模型,并得出不同位置接触面上相互作用力的差异分布。
2)通过数值模拟获得脱模力与脱模位移关系曲线以及特定阶段的位移云图,并结合断裂力学能量平衡理论揭示了模板与聚合物从黏结力逐步失效到完全分离的脱模规律和作用机理。
3)高宽比为2和1.5时,脱模力曲线有两个峰值;高宽比为1和0.5时,脱模力曲线有一个峰值;高宽比小于等于2时,高宽比减小,底部和顶部横向接触分离时的叠加效应使最大脱模力略有增加。
4)残余层厚度不影响最大脱模力的数值,但会影响最大脱模力出现时对应的脱模位移数值。聚合物凸起相同,残余层厚度越大,与同一脱模力相对应的脱模位移越大。
参考文献:
[1]CHOU S Y,KRAUSS P R,RENSTROM P J.Imprint of sub-25 nm vias and trenches in polymers[J].Applied Physics Letters,1995,67(21):3114-3116.
[2]RYU J H,LIM H J,LEE S H,et al.Polymer filling ratio with various pressure variation rates in nanoimprint lithography[J].Microelectronic Engineering,2014,131:24-28.
[3]TAYLOR H,LAM Y C,BONING D.An investigation of the detrimental impact of trapped air in thermoplastic micro-embossing[J].Journal of Micromechanics and Microengineering,2010,20(6):1023-1035.
[4]贺永,傅建中,陈子辰.微热压印过程中聚合物流动形貌的研究[J].光学精密工程,2008,16(2):270-278.
HE Yong,FU Jianzhong,CHEN Zichen.Study on polymer flow profile in micro hot embossing[J].Optics and Precision Engineering,2008,16(2):270-278.
[5]KIM S M,KANG J H,LEE W I.Analysis of polymer flow in embossing stage during thermal nanoimprint lithography[J].Polymer Engineering and Science,2011,51(2):209-217.
[6]王清,张睿,张金涛,等.热压印聚合物成型体脱模过程中接触脱离分析[J].山东科技大学学报(自然科学版),2015,34(5):1-5.WANG Qing,ZHANG Rui,ZHANG Jintao,et al.Contact detaching analysis of imprinted polymers during demolding in thermal imprint lithography[J].Journal of Shandong University of Science and Technology(Natural Science),2015,34(5):1-5.
[7]汤启升,金建,李鑫,等.卷对卷纳米压印脱模过程的有限元模拟[J].真空,2012,49(3):31-34.
TANG Qisheng,JIN Jian,LI Xin,et al.Finite element analysis on the demolding process of the micro-patterns in roll-to-roll nanoimprint lithography[J].Vacuum,2012,49(3):31-34.
[8]SONG Z C,CHOI J,YOU B H,et al.Simulation study on stress and deformation of polymeric patterns during the demolding process in thermal imprint lithography[J].Journal of Vacuum Science and Technology B:Microelectronics and Nanometer Structures,2008,26(2):598-605.
[9]黄平,郭丹,温诗铸.界面力学[M].北京:清华大学出版社,2013:18-43.
[10]赵亚溥,王立森,孙克豪.Tabor数、黏着数与微尺度黏着弹性接触理论[J].力学进展,2000,30(4):529-537.
ZHAO Yapu,WANG Lisen,SUN Kehao.Tabor number adhesion parameter and elastic theory of microscale adhesive contact[J].Advances in Mechanics,2000,30(4):529-537.
[11]MAUGIS D.Adhesion of sphere:The JKR-DMT transition using a dugdale model[J].Journal of Colloid and Interface Science,1992,150(1):243-269.
[12]POLLOCK H M,MAUGIS D,BARQUINS M.Force of adhesion between solid-surfaces in contact[J].Applied Physics Letters,1978,33(9):798-799.
[13]郭育华,刘刚,朱学林,等.热模压成型技术中的脱模研究[J].中国机械工程,2005,16(增1):432-434.
GUO Yuhua,LIU Gang,ZHU Xuelin,et al.Study on demolding process during hot embossing[J].China Mechanical Engineering,2005,16(S1):432-434.
[14]DERJAGUIN B V,MULLER V M,TOPROV Y P.Effect of contact deformation on the adhesion of particles[J].Journal of Colloid and Interface Science,1975,53(2):314-326.
[15]LAN H B,DING Y C,LIU H Z,et al.Mold deformation in soft UV-nanoimprint lithography[J].Science in China Series E:Technological Sciences,2009,52(2):294-302.
[16]程靳,赵树山.断裂力学[M].北京:科学出版社,2006:9-39.
(责任编辑:李磊)
Mechanism Analysis of Demolding Process in Nano-imprint Lithography
MA Lijun,WANG Qing,ZHANG Rui,ZHANG Jintao,ZHENG Xu
(College of Civil Engineering and Architecture,Shandong University of Science and Technology,Qingdao,Shandong 266590,China)
Abstract:To reduce product defects caused by demolding process,the demolding mechanism in nano-imprint lithography was studied.A theoretical model about acting force between the mold and the polymer was proposed based on contact theory in interface mechanics.Then contact separating between the mold and the polymer was simulated by using ANSYS.The rules and mechanism of demolding were obtained by analyzing the relations between the demolding force and the displacement in terms of energy balance theory in fracture mechanics.The results show that there are significant differences in acting forces on various contact surfaces in demolding process.There are two peaks in the demolding force curve when the aspect ratio is 2 and 1.5,but there is one peak in the demolding force curve when the aspect ratio is 1 and 0.5.With the increase of residual layer thickness,the demolding displacement corresponding to the same demolding force increases,but the value of maximum demolding force is unaffected.
Key words:demolding process;mechanism;contact;adhesion force;demolding force;demolding displacement
收稿日期:2015-12-05
基金项目:山东省“泰山学者”建设工程专项资金项目(TSHW 20130956)
作者简介:马立俊(1991—),男,山东聊城人,硕士研究生,主要从事微纳米成型与表面功能化研究. 王清(1966—),男,河北石家庄人,教授,博士生导师,主要从事功能材料与智能结构、微纳米成型与表面功能化研究,本文通信作者.E-mail:profqwang@163.com
中图分类号:TN405
文献标志码:A
文章编号:1672-3767(2016)03-0078-07

