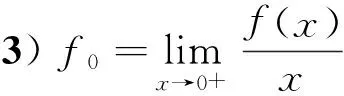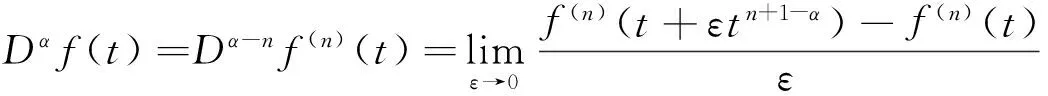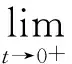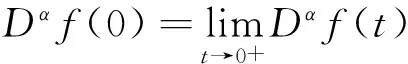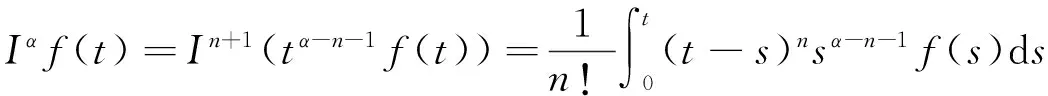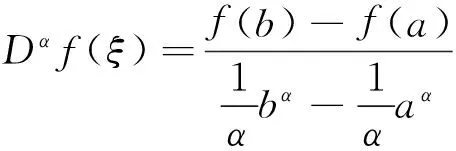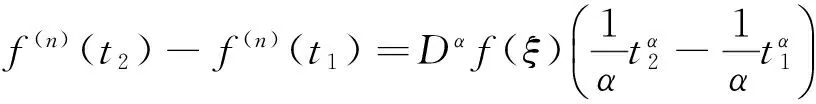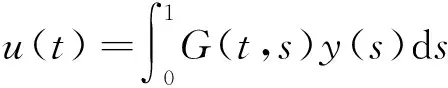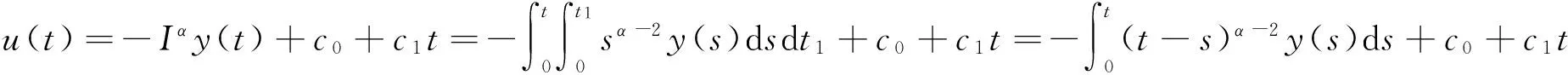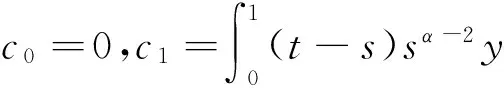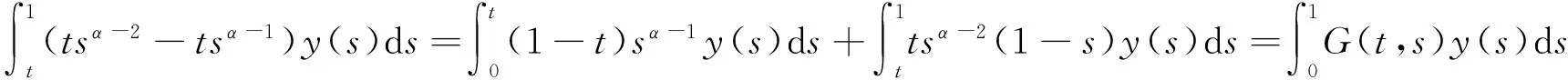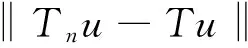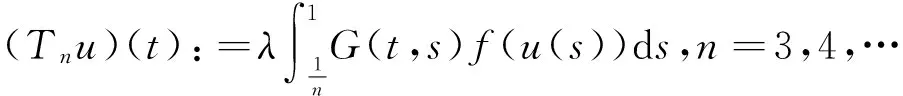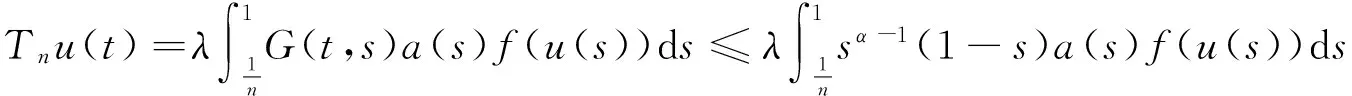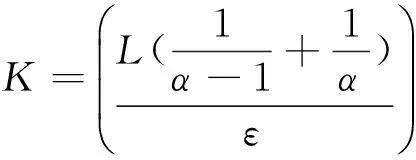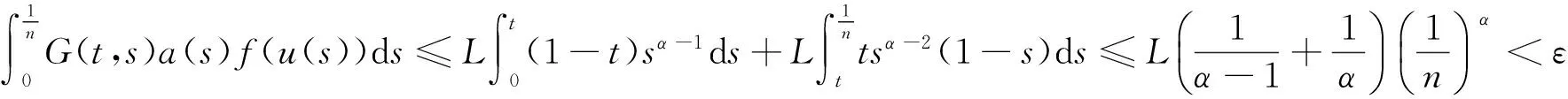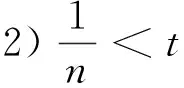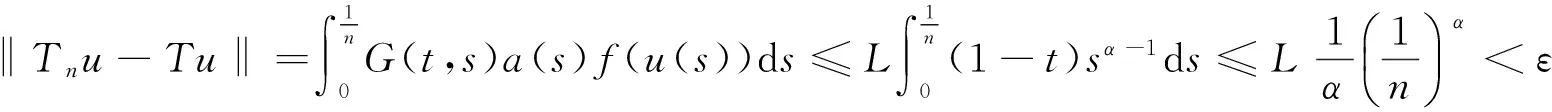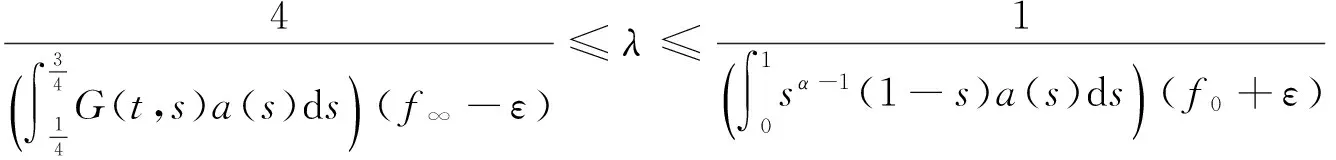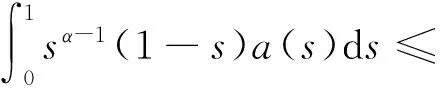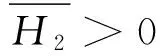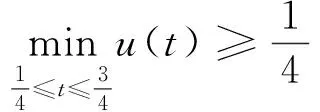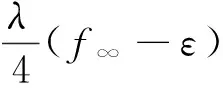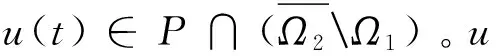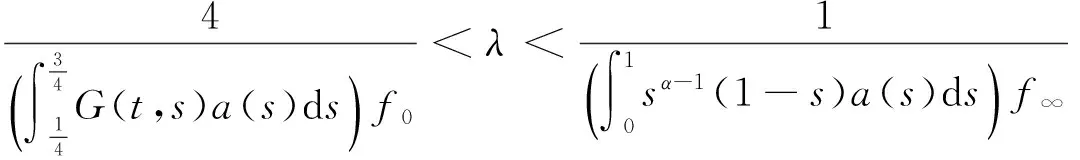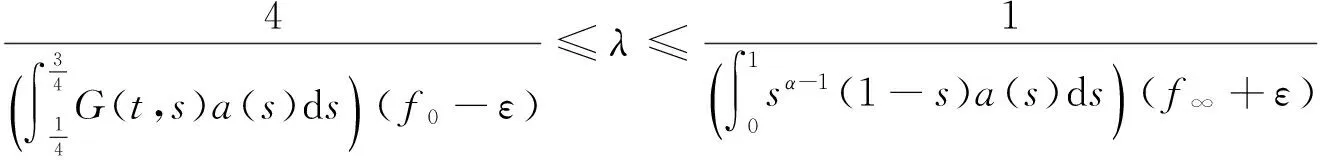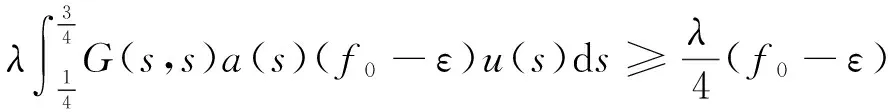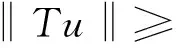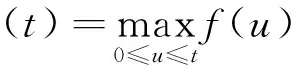具有适型分数阶导数的非线性特征值问题的正解

董晓玉，白占兵，张　伟

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

具有适型分数阶导数的非线性特征值问题的正解

董晓玉，白占兵，张伟

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

摘要：本文研究具有适型分数阶导数的非线性特征值问题正解的存在性。首先给出Green函数G(t,s)并且证明其非负标和有界性；其次，利用Krasnosel’skii不动点定理对该问题的特征值区间给以刻划，得到正解的存在性和多解性。

关键词：适型分数阶导数；非线性特征值问题；奇异Green函数；Krasnosel’skii不动点定理

1引言

近年来，分数阶微积分和分数阶微分方程在众多领域应用广泛，例如动力系统[1-2]、生物工程[3-4]、信号分析[5-6]、图像处理[7]等。其中Henderson等[8]在1997年用Krasnosel′skill不动点定理研究了如下整数阶的非线性特征值问题的正解：

u″(t)+λa(t)f(u)=0,0

u(0)=u(1)=0。

2012年Bai等[9]考虑了下列分数阶微分方程边值问题：

CDαu(t) + λh(t)f(u(t)) = 0,0 < t < 1,

u(0)=u′(1)=u″(0)=0。

其中，20。在一些假设下，利用锥上的不动点定理得到所研究问题的特征区间。

基于此，本论文研究最近刚给出的适型分数阶导数的非线性特征值问题：

Dαu(t)+λa(t)f(u(t))=0,0

(1)

u(0)=u(1)=0。

(2)

其中，1

1) f:[0,1]×[0,∞)→[0,∞)是连续的，

2) a:[0,1]→[0,∞)连续且在任意子区间上不恒等0，

据我们了解，已有的关于边值问题的文章[8-9,10,12]所涉及到的Green函数都是连续的，但本文所处理的问题其Green函数是奇异的。

本文结构如下，第二部分给出适型分数阶导数的一些相关定义并且给出相应的Green函数；第三部分证明定义的积分算子是连续的，利用Krasnosel′skill不动点定理得到所考虑问题存在正解的特征值区间。

2预备知识

为了读者的方便，此处给出一些微积分理论必要的定义。

定义 2.1[10]连续函数f:(0,∞)→R的α∈(n,n+1]阶适型分数阶导数定义为

(3)

(4)

注 2.1给定α∈(n,n+1]，有

Dαtk=0,

其中k=0,1,…,n。

引理2.1设t>0,α∈(n,n+1]。函数f(t)是(n+1)阶可微函数当且仅当f是α阶可微的，并且

Dαf(t)=tn+1-αf(n+1)(t)。

证明设h=εtn+1-α+O(ε2)，根据定义2.1，有

证毕。

定义2.2[9]连续函数f:(0,∞)→R的α∈(n,n+1]分数积分定义为

(5)

其中In+1是n+1阶积分算子。

引理2.2设α∈(n,n+1]。f在Iα的定义域下是一个连续函数，t≥0时DαIαf(t)=f(t)。

证明因为f(t)是连续的，那么Iαf(t)是(n+1)阶可微的。由引理2．1有

tn+1-αf(t)tα-n-1=f(t)。

证毕。

引理2.3[9](中值定理)设a≥0，f:[a,b]→R具有以下性质

1)f在[a,b]上是连续的，

2) 对于α∈(0,1)，f在(a,b)上是α阶可微的，

引理2.4设α∈(n,n+1]，t>0时，f是一个α阶可微函数，那么Dαf(t)=0，t∈[0,1]，当且仅当f(t)=a0+a1t+…+an-1tn-1+antn，其中ak∈R，k=0,1,…,n。

证明充分性由注2．1可证。 接下来，给定t1,t2∈[0,1]，t1

由Dαf(ξ)=0可知，f(n)(t2)=f(n)(t1)，又由t1,t2的任意性，有f(t)=a0+a1t+…+an-1tn-1+antn，t∈[0,1]。证毕。

根据引理2．2和引理2．4，立即有下述引理。

引理2.5设α∈(n,n+1]，u∈C(0,1)∩L(0,1)具有α阶分数导数并属于C(0,1)∩L(0,1)。那么

IαDαu(t)=u(t)+c0+c1t+…+cntn,

(6)

其中，ck∈R,k=0,1,…,n。

在以下的讨论中，假设α∈(1,2]。

下面给出线性分数阶微分方程边值问题的Green函数。

引理 2.6假设y∈C[0,1]，则问题

Dαu(t)+y(t)=0,0

(7)

u(0)=u(1)=0,

(8)

的唯一解是

其中

(9)

证明：利用引理2．5可推出方程(7)等价于积分方程

证毕。

显然α=2时，式(9)即是通常的Green函数。

引理2.7由式(9)定义的Green函数G(t,s)满足以下性质：

1)G(t,s)>0，对任意的t,s∈(0,1)；

证明：由G(t,s)的表达式可知，G(t,s)>0，对t,s∈(0,1)成立。下面，对给定的s∈(0,1)可求出G(t,s)关于t的偏导数，

由此可知G(t,s)关于t在s≤t时是递减的，t≤s时是递增的。

因此，

且

设

此处Green函数有一个常数界，这在Riemann-Liouville导数下是无法做到的[11]。

1)‖Ax‖≤‖x‖，x∈P∩∂Ω1，且‖Ax‖≥‖x‖，x∈P∩∂Ω2，或

2)‖Ax‖≥‖x‖，x∈P∩∂Ω1，且‖Ax‖≤‖x‖，x∈P∩∂Ω2

3主要结果

本文考查特征值问题(1)，(2)的可解性。由引理2．6知u(t)是问题(1)，(2)的解，当且仅当

设常数τ∈[0,1]，定义如下

定义积分算子T,Tn:P→E为

引理3.1T:P→P是全连续算子。

证明：首先，证明Tn,n=3,4,…是一列全连续算子。由引理2．7，a(s)和f(u)的非负性可知，对于任意的t∈[0,1]，u∈P,Tnu(t)≥0，且

所以，

(11)

对u∈P，由引理2．7和(11)式得

因此，Tn是保锥映射。另外，标准的讨论得Tn:P→P全连续。

显然T:P→P。接下来证Tn:P→P一致收敛于T，从而T:P→P也是全连续算子。

任意的ε>0，令

则当n>K时，有‖Tnu-Tu‖<ε。分两种情况考虑：

由引理2．8，T:P→P全连续。证毕。

定理3.1假设条件(A)，(B)和(C)都满足。那么，只要λ满足

(12)

边值问题(1)，(2)至少有一个解。

证明：设λ是(12)式中给定的。选取ε>0使得

由引理3．1知，T:P→P是全连续算子。对上述ε>0，由f0的定义知，存在H1>0，使得f(x)≤(f0+ε)x，0

Ω1:={u∈P|‖u‖

对于u∈∂Ω1，0

因此，u∈P∩∂Ω1时‖Tu‖≤‖u‖。

Ω2:={u∈P|‖u‖

因此，u∈P∩∂Ω2时‖Tu‖≥‖u‖。

定理 3.2假设条件(A)，(B)和(C)都满足。且

(13)

则边值问题(1)，(2)至少有一个解。

证明：设λ是(13)式中给定的。选取ε>0使得

Ω1:={u∈P|‖u‖

有

Ω2:={u∈P|‖u‖

如果u∈P∩∂Ω2，有

参考文献：

[1]MERALF,ROYSTONT,MAGINR.Fractionalcalculusinviscoelasticity,Anexperimentalstudy[J].CommunicationsinNonlinearScienceandNumericalSimulation,2010,15(14):939-945.

[2]武华华,孙苏菁.基于变分方法的四阶边值问题的多重正解[J].山东科技大学学报(自然科学版),2014,33(2):96-99.

WUHuahua,SUNSujing.Basedonthevariationalmethodofthemultiplepositivesolutionsoffourth-orderboundaryvalueproblem[J].JournalofShandongUniversityofScienceandTechnology(NaturalScience),2014,33(2):96-99.

[3]OLDHAMK,SPANIERJ.Thefractionalcalculus[M].NewYork:AcademicPress,1974:27-36.

[4]PODLUBNYI.Fractionaldifferentialequations[M].NewYork:AcademicPress,1999:50-65.

[5]KILBASA,SRIVASTAVAH,TRUJILLOJ.Theoryandapplicationsoffractionaldifferentialequations[M].Amsterdam,ElsevierScienceB.V.,2006:78-84.

[6]WEITZNERH,ZASLAVSKYG.Someapplicationsoffractionalequations[J].CommunicationsinNonlinearScienceandNumericalSimulation,2003,8(3/4):273-281.

[7]MACHADOJ,KIRYAKOVAV,MAINARDIF.Recenthistoryoffractionalcalculus[J].CommunicationsinNonlinearScienceandNumericalSimulation,2011,16(3):1140-1153.

[8]HENDERSONJ,WANGH.Positivesolutionsfornonlineareigenvalueproblems[J].JournalofMathematicalAnalysisandApplications,1997,208(1):252-259.

[9]BAIZ.Eigenvalueintervalsforaclassoffractionalboundaryvalueproblem[J].Computers&MathematicswithApplications2012,64(10):3253-3257.

[10]LIUZ,LIF.MultiplePositivesolutionsofnonlineartwo-pointboundaryvalueproblem[J].JournalofMathematicalAnalysisandApplications,1996,203(3):610-625.

[11]KHALILR,HORANIM,YOUSEFAandSABABHEHM.Anewdefinitionoffractionalderivative[J].JournalofComputationalandAppliedMathematics,2014,264(5):65-70.

[12]BAIZ,LVH.Positivesolutionsofboundaryvalueproblemsofnonlinearfractionaldifferentialequation[J].JournalofMathematicalAnalysisandApplications,2005,311(4):495-505.

[13]郭大钧.非线性泛函分析[M].2版.济南:山东科学技术出版社,2001:21-22.

(责任编辑：傅游)

Positive Solutions for Nonlinear Eigenvalue Problems with Conformable Fractional Differential Derivatives

DONG Xiaoyu, BAI Zhanbing, ZHANG Wei

(College of Mathematics and Systems Science, Shandong University of Science and Technology,Qingdao, Shandong 266590, China)

Abstract:This paper established the existence of positive solutions for nonlinear eigenvalue problems with conformable fractional differential derivatives Firstly, Green's function was given and its properties were proved. Secondly, by using Krasnosel'skii fixed-point theorems, the interval of eigenvalue problems was investigated and its existence and multiplicity of positive solutions were acquired．

Key words:conformable fractional derivative; nonlinear eigenvalue problems; singular Green′s function; Krasnosel′skii fixed point theorem

收稿日期：2016-01-06

基金项目：国家自然科学基金项目(11571207)

作者简介：董晓玉(1992—)，女，山东青岛人，硕士研究生，主要从事分数阶微分方程的研究. 白占兵(1971—)，男，甘肃高台人，教授，博士，主要从事应用微分方程的研究，本文通信作者. E-mail：zhanbingbai@163.com

中图分类号：O175．1

文献标志码：A

文章编号：1672-3767(2016)03-0085-07