基于贝叶斯更新的双渠道联合库存与定价策略研究
赵 禹,周长银,王吉豪
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
基于贝叶斯更新的双渠道联合库存与定价策略研究
赵禹,周长银,王吉豪
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
摘要:本论文基于对网络市场需求的贝叶斯更新,分别讨论了双渠道库存共享和分开两种情况下最优联合库存与定价策略,并就总库存相同的情况下双渠道库存是否共享给出了决策方法。通过数值试验对两种模型做了比较,结果表明双渠道销售模式下库存共享策略优于库存分开策略。
关键词:动态定价;库存管理;贝叶斯更新;库存共享;双渠道
电子商务的发展和创新改变了人们的购物方式,也促使越来越多的商家由单一的传统渠道销售模式拓展到双渠道销售模式,这对降低营销渠道成本、扩大市场份额以及增加销售利润起到了重要的作用。近几年,双渠道销售模式成为联合库存和定价研究领域中的热点问题之一。同时,在网络渠道随机需求方面,由于贝叶斯更新方法更加接近现实情况,基于贝叶斯更新的联合库存和定价策略研究也受到越来越多的关注。
关于双渠道供应链的发展,许传永[1]将供应链的发展分为.com阶段、去中间化阶段和双渠道融合并存阶段,商品的销售渠道由传统渠道转移到网络渠道,进而双渠道模式相融合,实现双渠道总利润最大化。2003年Park和Keh[2]指出制造商选择双渠道时,双渠道供应链整体利润将增加,但零售商的利润将会减少;2005年Yao和Liu[3]通过对竞争模型的分析,指出两个销售渠道之间存在价格竞争,但价格竞争会促使传统渠道的发展。从双渠道供应链选择方面可知,双渠道模式会引起两个销售渠道的竞争,但竞争使双渠道模式优于单一渠道模式,使供应链总利润增大。
针对双渠道供应链的联合库存和定价策略问题,王虹等[4]研究了制造商在网络渠道上的定价和库存决策以及零售商在传统渠道上的最优订货量;徐峰等[5]分别讨论了零售商市场份额、网络渠道销售成本和价格弹性系数等因素对双渠道最优定价策略的影响;金磊等[6]研究了零售商在单个时期下的双渠道库存和定价。上述文献从多个方面讨论了双渠道下的最优库存与定价策略,但是大部分都是基于单个时期的双渠道库存和定价策略。而在实际中,单个周期的决策不一定是最优决策,需要从多个周期考虑双渠道下的库存和定价策略问题。因此,本文在金磊等[6]研究的基础上,分别在双渠道库存共享和库存分开下,研究了动态定价模型,以判断双渠道库存是否共享。
在单个零售商多期的双渠道销售问题方面,贝叶斯方法很好地解决随机需求带来的问题,利用先验分布来处理不确定因素。Scarf[7]是在库存问题中最早利用贝叶斯方法的,而Whitin[8]是最早将定价和库存结合起来进行研究的;Zhang等[9]讨论了同时定价和库存的控制与学习, 研究了多维度状态空间中的贝叶斯模型;柳键等[10]利用贝叶斯公式对需求函数不断学习更新,研究了缺货和延迟交货情况下的动态定价和库存问题。本文探讨了贝叶斯更新方法对双渠道联合库存与定价策略的影响,在柳键等[10]研究的基础上,把单一渠道销售模式拓展到双渠道销售模式,并只对网络渠道的需求函数进行贝叶斯更新,而将传统渠道的需求函数假设为价格的一次函数,参考Li等[11]的多期动态模型建立本文的多期动态模型。
1模型假设及动态定价模型
1.1模型假设
在上述假设的基础上,根据双渠道模型的需要,本文还有如下假设:
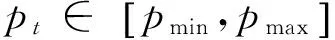
1.2零售商双渠道库存共享下的动态定价模型
零售商双渠道库存共享下,动态定价模型和单一渠道模型相同,因此,本文参考了柳键等[10]的模型,得到第t周期双渠道库存共享情况下的动态定价模型:
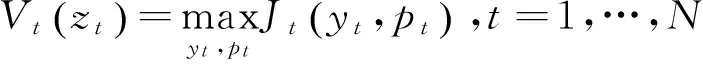
(1)
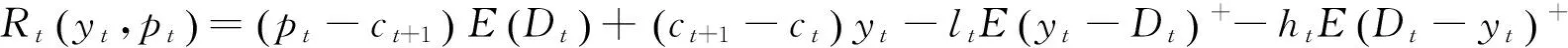
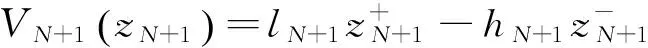
1.3零售商双渠道库存分开下的动态定价模型
在零售商双渠道库存分开情况下,和单一渠道模型不同,根据本文提出的假设可知:
设第t周期的网络渠道的期望成本为
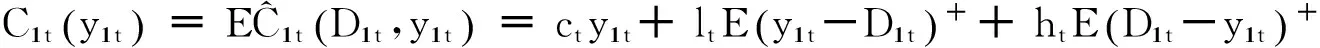
则零售商在网络渠道下的第t周期的利润为
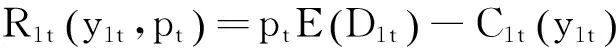
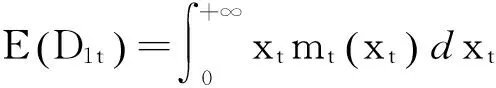
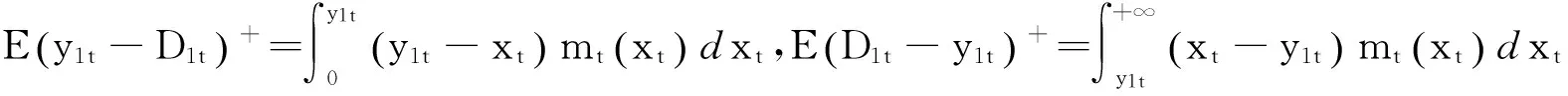
设第t周期传统渠道的期望成本为
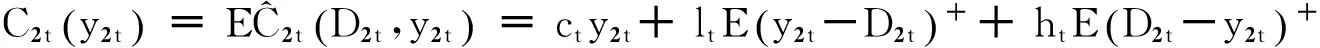
则零售商在传统渠道下的第t周期的利润为:
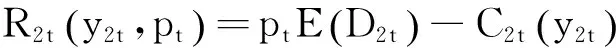
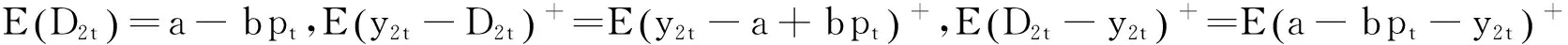
于是得到双渠道库存分开情况下的动态定价模型:
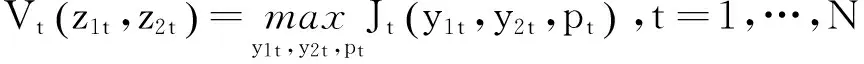
(2)
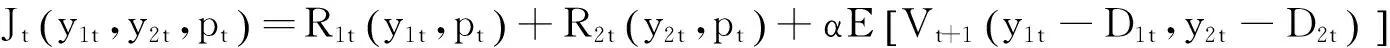
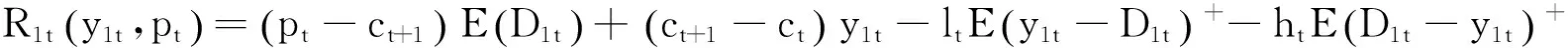
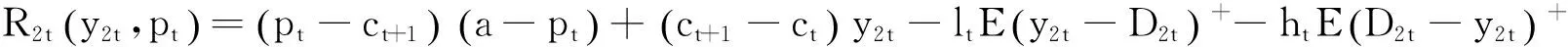
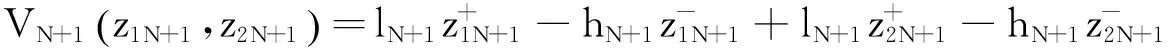
z1t=y1t-D1t,z2t=y2t-D2t。
2相关结论
对零售商双渠道库存共享和库存分开模型进行分析,来研究最优动态模型的定价与库存。
定理1对于t=1,…,N,有如下结论:
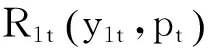
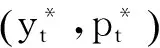
证明根据前面定理1和2,可由反证法证明出上面结论。
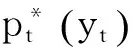
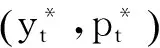
证明:由前面定理1、2、3、4,可得出此结论。
3数值分析
3.1数值模拟
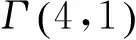
首先研究零售商在双渠道库存共享下最优动态定价模型,对于第一个销售周期:
对于第二个销售周期:
对上面库存共享下的模型进行编程,得到最优定价、最优库存以及相对应的利润。同理,对库存分开的模型也进行如上分析,然后编程得到优定价、最优库存以及相对应的利润。本文数据是在联想一体机Windows8系统下,利用Matlab编程,根据输入不同的库存和价格,就可以得到这个价格的最优库存以及相对应的利润,进而得到图1和图2。
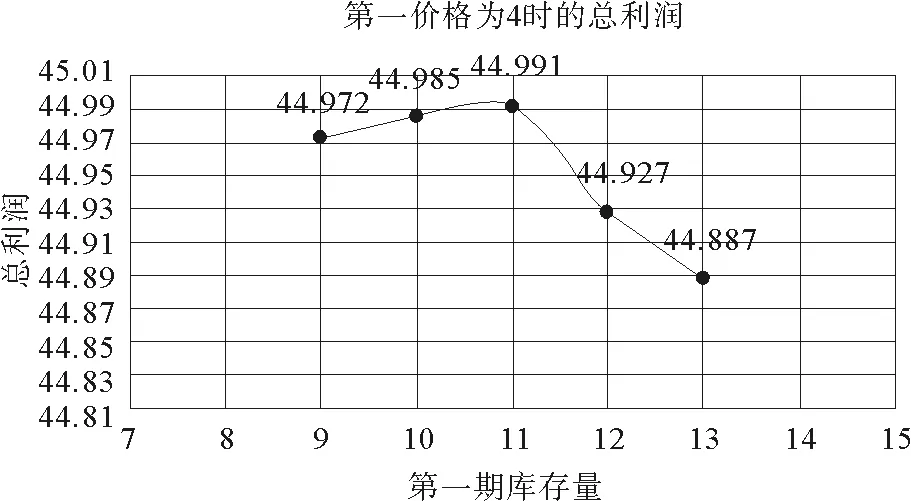
图1 库存共享模型的库存与总利润的关系图
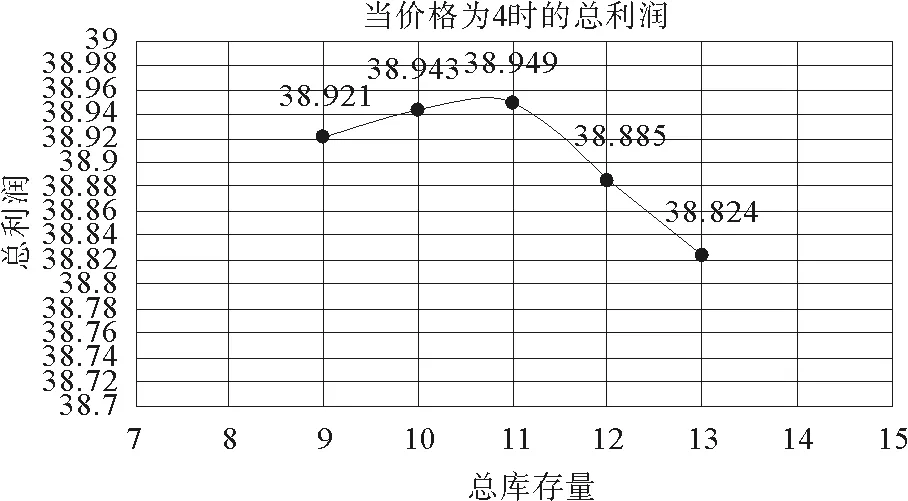
图2 库存分开模型的库存与总利润的关系图
由图1可以得到:当零售商采取双渠道库存共享时,这时候第一期的价格为p1=4,库存为y1=11,这时候零售商双渠道利润之和为44.991。而图2为零售商采取双渠道库存分开的情况,在第一期价格为p=4,总库存为y=11的时候,传统渠道和网络渠道的最优库存分别为y11=4,y21=7,这时候零售商双渠道利润之和为38.949。说明在总库存相同时,库存共享时的利润大于库存分开时的利润,故零售商应该采取双渠道库存共享。
3.2数值对比分析
根据本文的模型,从表1可以看出,库存共享时,零售商双渠道利润之和为44.991;而库存分开时,零售商双渠道利润之和最大为38.949。根据金磊等[6]研究的实例中,看出库存共享时的总利润为1612.5,而库存分开时,只有n1=20,n2=60时,总利润才能达到161 2.5。
通过本文的表1和金磊等[6]的数值实验进行对比。相同之处:在总库存相同时,都是库存共享策略优于库存分开策略;不同之处: 表1中库存分开时的最优利润是比库存共享时的最优利润小,而金磊等的数值实验库存分开时的最优利润和库存共享时的最优利润相等。
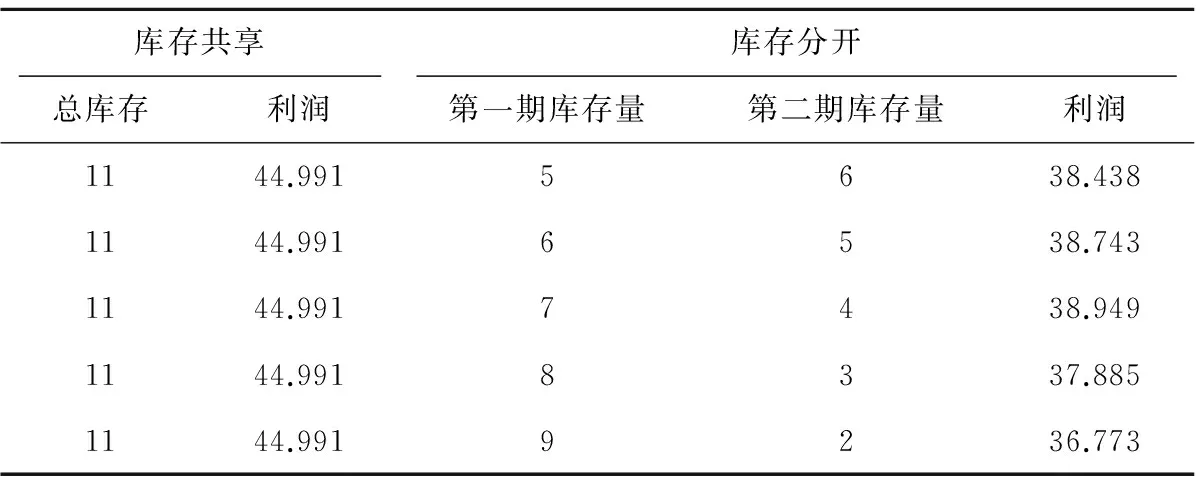
表1 库存共享和分开模型的总利润比较
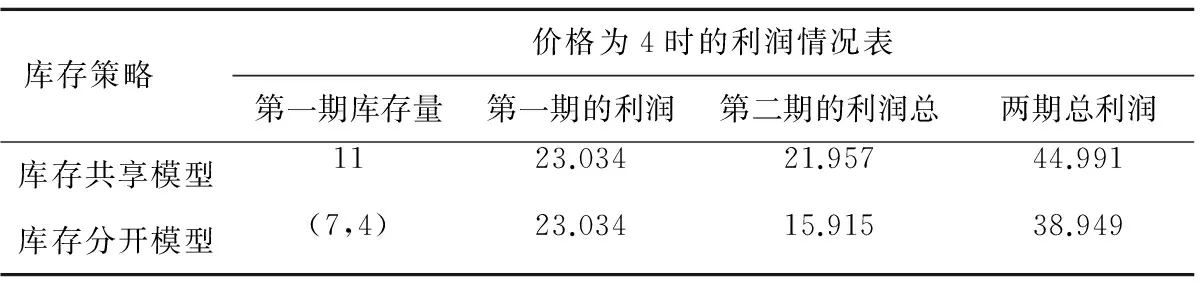
表2 两种库存模型总利润的比较
库存共享模型和库存分开模型之所以得到不同的结果,从数值实验上可以从表2得出,第一期的利润都为23.034,而第二期的利润却不相等,故两期总利润不相等。从模型上分析,金磊等的网络渠道商品为动态定价,传统渠道商品价格为定值;而本文研究的是多期双渠道商品同一动态定价,并且本文对网络渠道市场需求进行贝叶斯更新,故得到不同的结果。
4结束语
本文考虑了两种模型,即双渠道库存共享模型和库存分开模型;在多期的贝叶斯更新下的需求中,考虑了双渠道需求函数下的库存问题,研究在总库存相同的情况下,零售商的传统渠道和网络渠道的库存是分开还是共用一个库存。通过数值实验证明了双渠道下库存共享策略优于库存分开策略。本文把总的需求分为两个渠道的需求,并把传统渠道的需求为价格的一次函数,而现实中还有许多其他情况;本文研究是单一商品,而在现实中销售多个可以替代的商品,这也是以后需要研究的方向。
参考文献:
[1]许传永.两层双渠道供应链的优化与协调若干问题研究[D].合肥:中国科学技术大学, 2009.
[2]PARKHTK,KEHHT.Modelinghybriddistributionchannelsagame-theoreticanalysist[J].JournalofRetailingandConsumerServices,2003,10(3):155-167.
[3]YAODQ,LIUJJ.Competitivepricingofmixedretailane-taildistributionchannels[J].Omega,2005,33(1):235-247.
[4]王虹,周晶,孙玉玲.双渠道供应链的库存与定价策略研究[J].工业工程,2011,14(4):58-62.
WANGHong,ZHOUJing,SUNYuling.Integratedpricingandinventoryanalysisindualchannelsupplychain[J].IndustrialEngineeringJournal,2011,14(4):58-62.
[5]徐峰,侯云章,高俊.电子商务背景下制造商渠道定价与再制造策略研究[J].管理科学,2014,27(2):74-81.
XUFeng,HOUYunzhang,GAOJun.Astudyonmanufacturer'schannelpricingandremanufacturingstrategiesbasedone-commercebackground[J].JournalofManagementScience,2014,27(2):74-81.
[6]金磊,陈伯成,肖勇波.双渠道下库存与定价策略的研究[J].中国管理科学,2013,21(3):104-112.
JINLei,CHENBocheng,XIAOYongbo.Thestudyoninventoryandpricingstrategybetweenon-lineandphysicalchannels[J].ChineseJournalofManagementScience,2013,21(3):104-112.
[7]SCARFHE.Bayessolutionofthestatisticalinventoryproblem[J].AnnalsofMathematicalStatistics,1959,30(2):490-508.
[8]WHITINTT.Inventorycontrolandpricetheory[J].ManagementScience,1955,2(l):61-80.
[9]ZHANGJL,CHENJ.Bayesiansolutiontopricingandinventorycontrolunderunknowndemanddistribution[J].OperationsResearchLetters,2006,34:517-524.
[10]柳键,罗春林.基于贝叶斯信息更新的动态库存与定价研究[J].数理统计与管理,2011,30(4):724-730.
LIUJian,LUOChunlin.Dynamicinventoryandpricingbasedontheinformationupdatedbybayesformula[J].JournalofAppliedStatisticsandManagement,2011,30(4):724-730.
[11]LIQ,ZHENGS.Jointinventoryreplenishmentandpricingcontrolforsystemswithuncertainyieldanddemand[J].OperationsResearch,2006,54(4):696-705.
(责任编辑:傅游)
Joint Inventory and Pricing Strategy with Dual Channel Based on Bayesian Updating
ZHAO Yu, ZHOU Changyin, WANG Jihao
(College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, Shandong 266590, China)
Abstract:This paper researched on the issue of whether the retailer's inventory of the same product should be shared in the dual channel sales model. Based on the bayesian updating of a network market demand, the optimal joint inventory and pricing strategies in both the dual channel inventory sharing and the dual channel inventory separation were discussed and a decision making method was proposed on whether the dual channel inventory should be shared when the total inventory was the same. A comparison was made between the two models by numerical experiments and the results show that the dual channel sales mode inventory sharing strategy is superior to the inventory separation strategy.
Key words:dynamic pricing; inventory management; bayesian updating; sharing of inventory; dual channel
收稿日期:2015-11-25
作者简介:赵禹(1988—),男,山东邹城人,硕士研究生,主要从事库存与供应链管理的研究. E-mail:zhaoyu262263908@126.com 周长银(1970—),男,山东泰安人,副教授,主要从事随机最优化方法及应用、库存与供应链管理的研究.
中图分类号:F272
文献标志码:A
文章编号:1672-3767(2016)03-0106-06

