带乘性噪声的随机控制系统鲁棒H2/H∞控制设计
(山东科技大学 电气与自动化工程学院,山东 青岛 266590)
带乘性噪声的随机控制系统鲁棒H2/H∞控制设计
蒋登辉,李艳
(山东科技大学 电气与自动化工程学院,山东 青岛 266590)
摘要:本文主要研究了状态方程和输出方程均带有多个噪声源的无限时域离散随机控制系统的H2/H∞控制器的设计问题。首先给出一个随机有界实引理(SBRL);然后,利用随机有界实引理和系统的精确可观测性,给出了随机控制系统最优解的存在定理。该定理表明随机H2/H∞控制设计与四个耦合的广义代数Riccati方程的解的存在性有关。最后,给出了一个仿真实例来说明设计的效用。
关键词:随机控制系统;随机有界实引理;精确可观测性;H2/H∞控制;广义代数Riccati方程
所谓的H2/H∞控制是指寻找一个控制器不仅满足H∞性能指标的要求,而且当最坏扰动存在时,使得H2成本函数最小。混合H2/H∞控制作为一种重要的鲁棒控制方法得到了广泛的研究,并在工程实际中得到了应用。文献[1-4]是针对于确定性系统而言的,文献[5]研究了离散时间马尔科夫跳变系统的混合H2/H∞控制,文献[6]考虑了利用Riccati方程的方法解决带有随机加性噪声的线性系统的问题,文献[7]则研究了不确定多时滞广义系统的鲁棒控制问题。文献[8]和[9]分别研究了H2/H∞控制在CDMA系统的随机功率控制和硬盘驱动器的抗干扰设计。
近年来,随着H2/H∞控制器的设计及其应用的逐渐普遍,带有乘性噪声的连续和离散时间系统的随机H∞控制和混合H2/H∞控制问题已经成为一个热门的研究课题。文献[10]给出了基于线性矩阵不等式的随机有界实引理,这一引理在随机H∞滤波器设计中起着非常重要的作用。文献[11]很好地解决了带乘性噪声的马尔可夫跳系统的精确可观测性和精确可检测性的问题,并提出了相应的PBH判据,对系统的鲁棒H2/H∞控制进行了详细的设计;文献[12]对状态依赖噪声的系统进行了讨论,获得了关于随机H2/H∞控制设计的成果。张维海等[13]针对一类状态和扰动依赖噪声的系统进行了H2/H∞控制器设计。尽管关于H2/H∞控制器设计理论已经十分成熟,但是考虑到工程实践中输出过程也受到噪声的影响的实际,例如在动力调谐陀螺中,过大的输出噪声会引起视轴的抖动较大,从而影响它的跟踪精度和稳定精度。因此本文研究状态方程和输出方程均带有多个噪声源的离散随机控制系统的H2/H∞控制器设计问题。
本文的主要内容安排如下:第一节介绍离散随机控制系统模型,并给出相关定义和重要引理;第二节提出设计目标和要求,并获得H2/H∞控制设计。第三节采用逆向迭代算法来求解四个广义代数Riccati方程,并对系统进行了数值仿真。第四节总结全文。
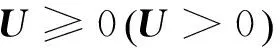
1带乘性噪声的随机控制系统模型和基本概念
本文考虑以下状态、控制输入和输出均带乘性噪声的随机控制系统:
(1)
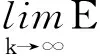
定义2[14]如果存在反馈矩阵F∈Rm×n使得闭环随机控制系统(1)是稳定的,那么随机控制系统(1)是可镇定的。
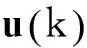

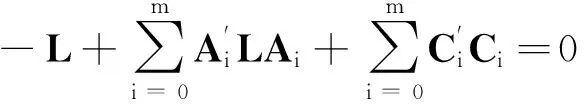
(2)
有唯一的解L≥0。
(3)
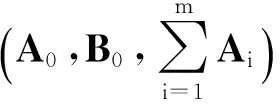
(4)
有唯一解L>0,而且
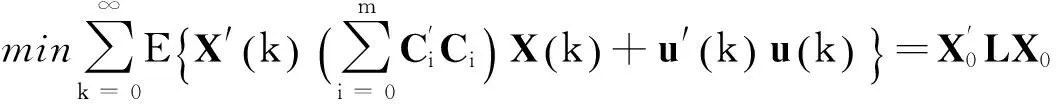
并且最优控制为
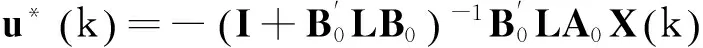
引理2由文献[16]中的引理3变换而来,两者证明过程基本相同,在此不再赘述。
接下来引进一个随机有界实引理。首先考虑下面的随机控制系统:
(5)
其中,v∈Rnυ是指外部干扰,Z∈Rnz是控制输出。
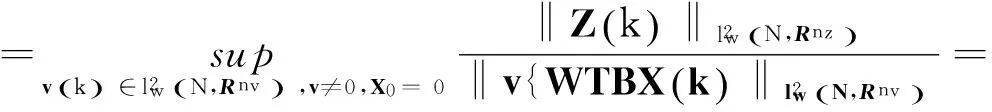
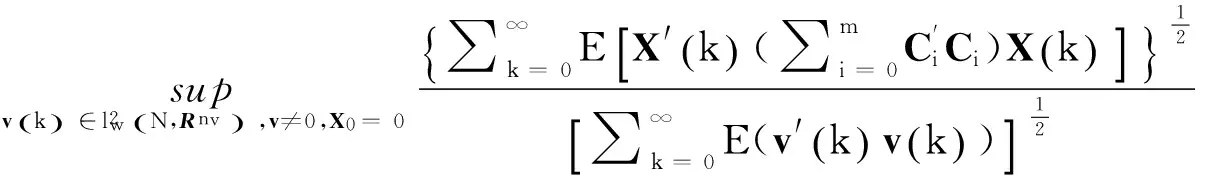
对文献[6]中的引理4做一个简单推广,可以得到以下引理:
引理3如果系统(5)是内部稳定的,并且对于任意给定的γ>0,满足‖Γ‖<γ,则下列广义代数Riccati方程
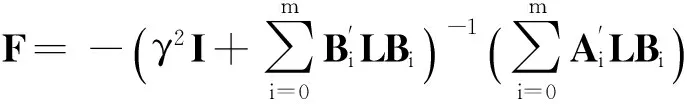
2无限时域离散随机控制系统的鲁棒H2/H∞控制设计
本节我们利用代数Riccati方程得出随机H2/H∞控制问题的解。考虑如下离散随机控制系统:
(7)
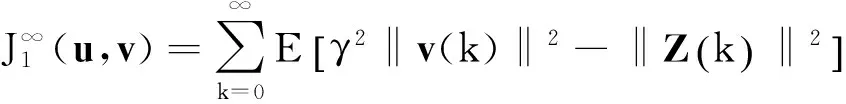
(8)

(9)
系统(7)的无限时域随机H2/H∞控制器设计要求如下:
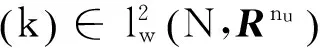
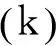
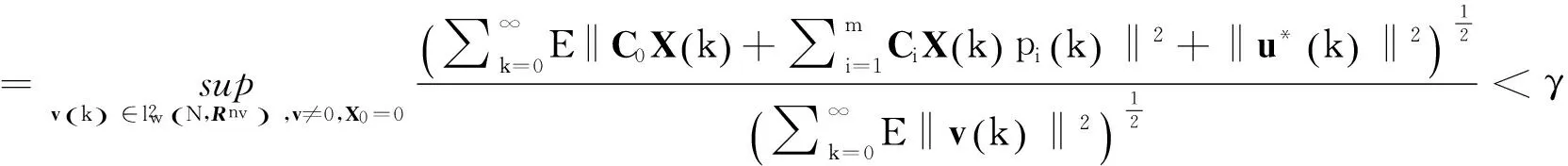
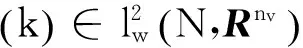
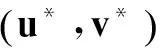
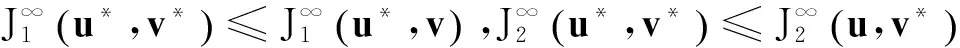
(10)
定理1对于系统(7),假设以下四个广义代数Riccati方程
(11)
(12)
(13)
(14)
(15)
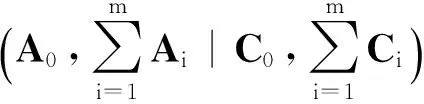
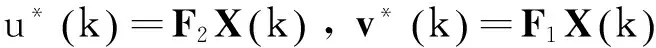
(16)
首先,给出引理4,将用于定理1的证明。
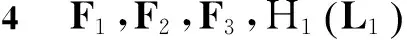
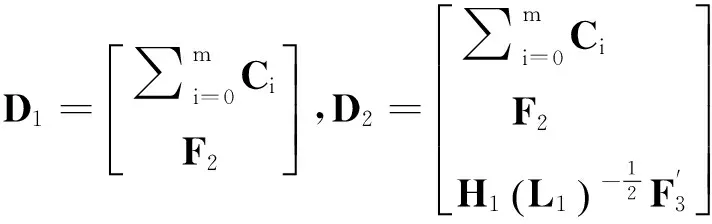
有以下结论:
定理1的证明分为以下三个步骤:
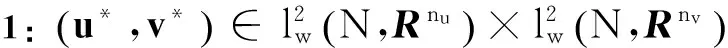
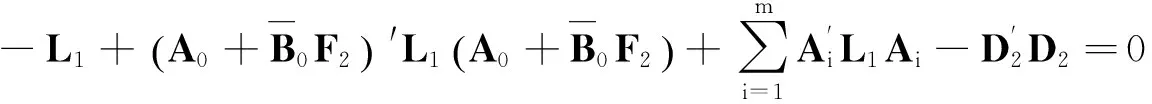
(17)
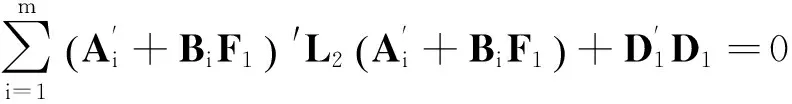
(18)
其中D1和D2的定义同引理4。
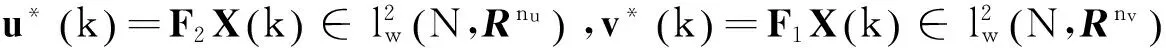
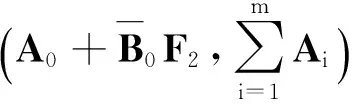
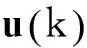
步骤3:当系统(7)中存在最坏的干扰v*时,u*同样会减少系统的输出能量。
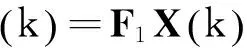
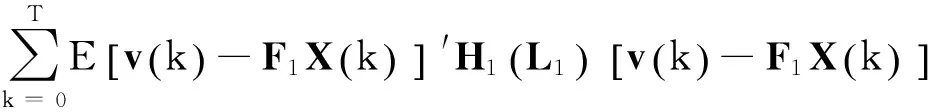
其中,
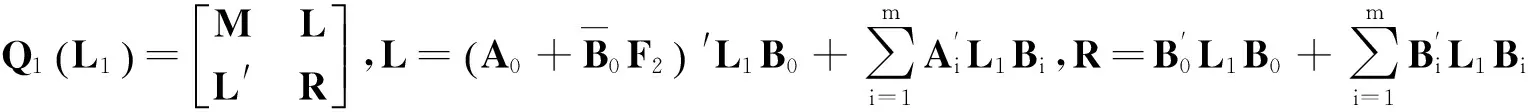
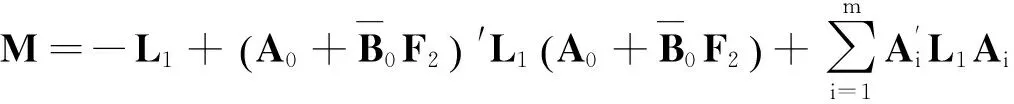
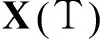
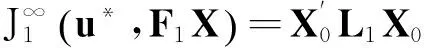
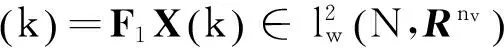
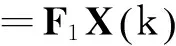
3数值仿真
本文采用逆向迭代算法来求解四个耦合方程(7)~(10)。给出下面的一个二维数值仿真,假设迭代次数是100次,在随机控制系统(1)中,假设m=2,γ=0.997,

通过运用逆向迭代算法,获得耦合方程(7)~(10)的最优解如下:
通过解可知,L1<0,L2>0。迭代过程如图1和图2所示,图中横坐标是迭代次数N,纵坐标是最优解L1(0)、L2(0)、F1和F2矩阵中每个元素的值,L1(0)、L2(0)为对称矩阵。图形清晰地表明了逆向迭代算法的收敛性和快速性。
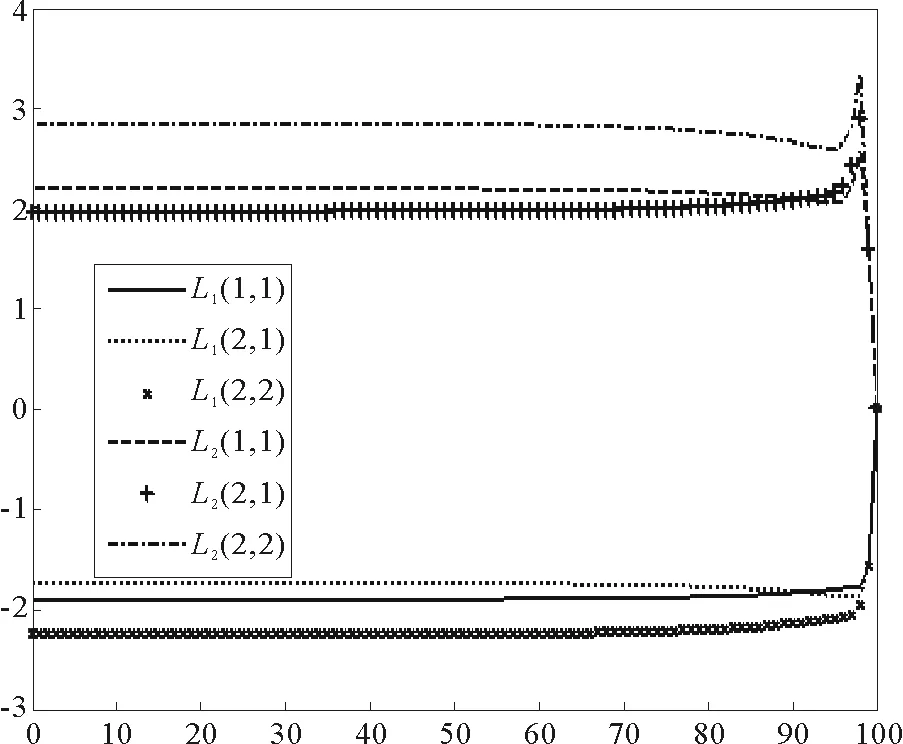
图1 L1和L2的迭代过程
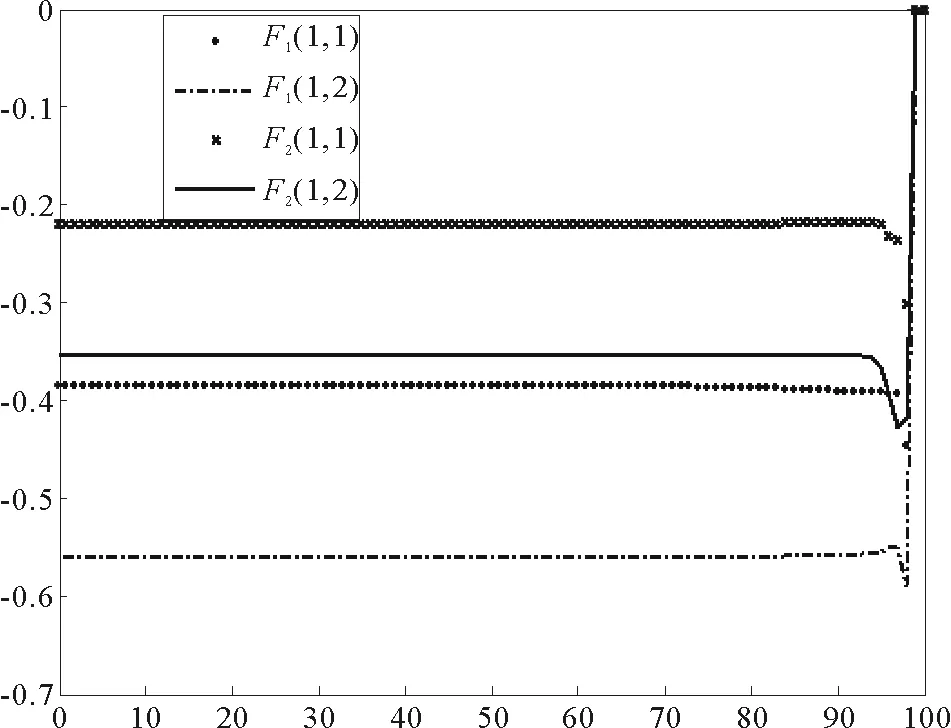
图2 F1和F2的迭代过程
4结论
本文研究了带乘性噪声的离散随机控制系统的控制器设计问题,通过精确可观测性和一个有界实引理,得出了最优的鲁棒H2/H∞控制设计,该设计与四个耦合的广义代数Riccati方程有关。使用逆向迭代算法对四个方程进行了求解,并通过数值仿真验证了算法的有效性和设计的正确性。
参考文献:
[1]BASART,BERNHARP.H∞-optimalcontrolandrelatedminimaxdesignproblems:Adynamicgameapproach[M].First.France:SpringerScience&BusinessMedia,1995:11-399.
[2]LIMEBEERD,ANDERSONB,HENDELB,etal.ANashgameapproachtomixedH2/H∞control[J].IEEETransactionsonAutomaticControl,1994,39(1):69-82.
[3]KHARGONEKARPP,ROTEAMA.MixedH2/H∞control:Aconvexoptimizationapproach[J].IEEETransactionsonAutomaticControl,1991,36(7):824-837.
[4]SZNAIERM,ROTSEINH.Anexactsolutiontogeneral4-blocksdiscrete-timemixedH2/H∞problemsviaconvexoptimization[J].IEEETransactionsonAutomaticControl,1994,43(10):2251-2256.
[5]COSTAOLV,MARQUESRP.MixedH2/H∞controlofdiscrete-timeMarkovianjumplinearsystems[J].IEEETransactionsonAutomaticControl,1998,43(1):95-100.
[6]CHENX,MOOREJB,ZHOUXY,etal.SolvabilityandasymptoticbehaviorofgeneralizedRiccatiequationsarisinginindefinitestochasticLQcontrols[J].IEEETransactionsonAutomaticControl,2001,46(1):428-440.
[7]王中凤,张高民,王玉芬.不确定多时滞广义系统的鲁棒H∞控制[J].山东科技大学学报(自然科学版),2009,28(2):106-110.
WANGZhongfeng,ZHANGGaomin,WANGYufen.RobustH∞controlforuncertaingeneralizedsystemswithmultipletime-delays[J].JournalofShandongUniversityofScienceandTechnology(NaturalScience),2009,28(2):106-110.
[8]QIANLJ,GAJICZ.VarianceminimizationstochasticpowercontrolinCDMAsystems[J].IEEETransactionsonWirelessCommunications,2002,5(1) :1763-1767.
[9]DUCL,XIELH,TEOHJN,etal.AnimprovedmixedH2/H∞controldesignforharddiskdrives[J].IEEETransactionsonControlSystemsTechnology,2005,13(5):832-839.
[10]ELBOUHTOURIA,HINRICHSEND,PritchardAJ.H∞-typecontrolfordiscrete-timestochasticsystems[J].InternationalJournalofRobustNonlinearControl,1999,9(13):923-948.
[11]侯婷.离散时间Markov跳变系统的稳定性和鲁棒H2/H∞控制[D].青岛:山东科技大学,2010:9-97.
[12]CHENBS,ZHANGWH.StochasticH2/H∞controlwithstate-dependentnoise[J].AutomaticControl,IEEETransactionson,2004,49(1):45-57.
[13]ZHANGWH,HUANGYL,ZhangHS.StochasticH2/H∞controlfordiscrete-timesystemswithstateanddisturbancedependentnoise[J].Automatica,2007,43(3):513-521.
[14]谭成.随机系统的稳定性、能观测性及能检测性研究[D].青岛:山东科技大学,2012:10-37.
[15]LIZY,WANGY,ZHOUB,etal.Detectabilityandobservabilityofdiscrete-timestochasticsystemsandtheirapplications[J].Automatica,2009,45(5):1340-1346.
[16]ZHANGWH,HUANGYL,XIELH.InfinitehorizonstochasticH2/H∞controlfordiscrete-timesystemswithstateanddisturbancedependentnoise[J].Automatic,2008,44(9):2306-2316.
(责任编辑:傅游)
Robust H2/H∞Control of Stochastic Control Systems with Multiplicative Noise
JIANG Denghui, LI Yan
(College of Electrical Engineering and Automation, Shandong University of Science and Technology,Qingdao, Shandong 266590, China)
Abstract:The paper mainly investigated the mixed H2/H∞control design of infinite horizon discrete-time stochastic control systems with multiplicative noise in both state and output equation. Firstly, a stochastic bounded real lemma (SBRL) was built. Secondly, on the basis of SBRL and exact observability, an optimal solution existence theorem of the stochastic H2/H∞control system was obtained, which indicates that the stochastic control design is related to the solution of the four coupled general algebraic Riccati equations (GAREs). Finally, a numerical example was proposed to illustrate the effectiveness of the design.
Key words:stochastic control system; stochastic bounded real lemma; exact observability;H2/H∞control; general algebraic Riccati equation
收稿日期:2015-12-31
基金项目:国家自然科学基金项目(61402265);山东科技大学群星计划项目(qx2013111)
作者简介:蒋登辉(1990—),女,山东泰安人,硕士研究生,主要从事随机鲁棒控制研究. E-mail:liyanghd@163.com
中图分类号:O231
文献标志码:A
文章编号:1672-3767(2016)03-0092-07
李艳(1975—),女,山东泰安人,讲师,博士,主要从事随机鲁棒控制研究,本文通信作者.

