基于结构灵敏度分析与稀疏约束优化的结构损伤识别方法

周述美， 鲍跃全， 李　惠

(哈尔滨工业大学 土木工程学院，哈尔滨　150090)

基于结构灵敏度分析与稀疏约束优化的结构损伤识别方法

周述美， 鲍跃全， 李惠

(哈尔滨工业大学 土木工程学院，哈尔滨150090)

摘要：在反问题求解中引入稀疏约束条件是当前应用数学领域的研究热点，结构损伤识别是典型的结构动力学反问题，且结构的损伤具有空间稀疏性，也即结构损伤发生时，只有部分单元或子结构出现损伤，基于结构灵敏度分析与稀疏约束优化，提出了一种结构损伤识别方法。通过结构灵敏度分析，建立结构损伤刚度参数的变化量与模态参数变化量之间的线性方程组，由于实测自由度有限，引入结构损伤稀疏性的条件，采用最小化l1范数优化求解。通过桁架模型的数值模拟，在考虑测量噪声的基础上，对多损伤工况进行了识别，与不考虑稀疏约束的损伤识别结果进行了对比,并对测点布置与数量对识别结果的影响进行了研究。仿真分析结果表明该方法可以在较少的测点下，有效地识别结构损伤的位置与程度，并且考虑稀疏约束可以明显增加损伤识别结果的准确性。

关键词：结构健康监测；结构损伤识别；压缩感知；结构灵敏度；稀疏约束优化

结构健康监测技术在世界范围内得到快速的发展和应用，我国在许多大跨度桥梁上安装了包括多种和较大规模传感器的健康监测系统[1-4]。结构损伤识别是结构健康监测的核心关键技术，在过去的几十年里，国内外研究者提出了大量基于振动测试的损伤识别方法的[5-7]。这些方法按照是否需要有限元模型的角度，可以分为非模型与基于模型的损伤识别方法。非模型的损伤识别方法，通过结构的振动响应数据，识别结构模态参数构造损伤指标，或直接从响应数据中，提取结构损伤特征构造损伤指标，然后再进行损伤定位。如，基于频率的结构损伤方法，通过结构频率改变构造合适的指标进行损伤诊断[8]。基于振型的结构损伤诊断方法，通过结构损伤前后振型的改变进行损伤诊断，如模态置信度判据法，曲率模态法、刚度法、柔度法、残余力向量法、模态应变能法等一些经典的方法。基于小波损伤特征提取方法[9]、基于信号分解变换的HHT(Hilbert Huang Translation)方法[10]、神经网络方法[11]、随机子空间损伤诊断技术[12]等。

有限元模型对结构损伤的精确定位与损伤程度的识别具有重要作用，基于模型的损伤识别方法通过结构振动响应数据提取的模态参数或损伤特征参数，结合有限元模型，识别结构系统参数，然后进行损伤识别。该类方法中，最重要的是识别过程中的优化求解问题，由于土木工程结构的复杂性以及实际测量信息的有限性，基于模型的损伤识别方法往往很难得到精确解。

近些年，国内外应用数学与信号处理领域提出了压缩感知(Compressive sensing)理论[13-15]，压缩感知理论的核心思想是只要某高维信号是可压缩的或在某个变换域上具有稀疏性，就可以用一个与变换基不相关的测量矩阵将该信号投影到一个低维空间上，然后通过求解一个最优化问题以极高的概率从这些少量的投影中重构出原始信号。压缩感知理论一提出就在许多研究领域得到的广泛的研究与应用[16]。从本质上讲, 压缩感知理论中的信号重构问题就是寻找欠定方程组的最稀疏解，压缩感知理论的提出也推动了稀疏优化问题求解方法的研究，对时间域、空间域或某些基变换下是稀疏的反问题的求解提供了新的思路。

结构损伤识别是典型结构动力学中的反问题，另外结构损伤是一种稀疏的现象，也即结构的损伤具有空间稀疏性。本文基于结构灵敏分析，引入稀疏约束条件，提出了一种结构损伤识别方法，并通过数值模拟验证了方法的有效性。

1结构灵敏度分析

对于一个n自由度结构系统，通过有限单元分析可得到n阶频率ωr和n阶振型φr(r=1,2,…,n)。不考虑阻尼的结构特征方程如下所示：

(1)

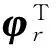
刚度和质量的改变会导致结构频率与振型等模态参数的变化，一般认为损伤只引起刚度的改变，采用结构模型中结构单元刚度系数的变化来表示结构的损伤。结构刚度矩阵可表示为

(2)

式中,θi为刚度损伤系数；Ki表示第i个单元的单元刚度矩阵；Ne表示单元数目。

振型和频率的灵敏度系数定义为：振型φr和频率ωr对刚度损伤系数θi的改变率，即有∂φr/∂θi和∂ωr/∂θi。灵敏度系数的大小可以表征相关单元的刚度变化对结构振型和频率的影响程度。

频率的灵敏度系数表达式为

(3)

振型灵敏度按照Zhao等[17]提出的方法进行推导，由泛函理论得知，在n维线性空间中，n个线性无关的向量称为空间的一组基。这组独立向量可以定义整个线性空间。又由于振动理论，结构振型之间是相互独立的，于是一组完整模态振型可以用来定义第r阶振型的灵敏度系数，振型灵敏度系数定义如下：

(4)

式中αl是一个待定系数，代表第l阶振型对振型灵敏度系数的权重。αl的取值分两种情况：

(5)

将αs代入式(4)即可得到振型灵敏度系数。

2结构损伤识别方法

单元的刚度变化量θ与实测结构模态参数的变化量Δγ可以通过灵敏度矩阵S建立如下联系：

Δγ=Sθ

(6)

式中，θ=[θ1,θ1,…,θNθ]T；S为灵敏度矩阵，

(7)

Sω=[Sω1,Sω2…,Sωn],

(8)

损伤引起结构模态参数的变化量表示为：

Δγ=[ΔωT,ΔφT]T

(9)

式中，Δω和Δφ为：

Δω=[Δω1,Δω2,…,Δωn]T,

(10)

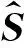
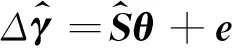
(11)

(12)

(13)

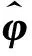
3稀疏正则化优化算法

式(11)建立了结构单元损伤刚度变化系数向量θ与测试的结构模态参数直接的关系，但向量θ的维数远大于测点数目，即未知数远多于方程数，式(11)为一病态的线性方程组，但结构单元损伤程度向量θ具有稀疏性，只有少数损伤的结构单元其值为非零，因此可通过如下方程优化求解

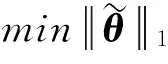
(14)

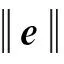
式(14)可以转换为无约束最小化问题：

(15)

步骤1：令λ0=1,l=1；

步骤2：代入式(16)优化求解

(16)

步骤4：λl=λl-1+Δλ，令l=l+1，并返回第2步。这里Δλ是λ的增量，本文算例中取Δλ=λ0/20。

4数值算例

建立一个桁架有限元模型，桁架总长度为8 m，每榀桁架的长度为0.4 m，总高度为0.8 m。结构共有312个杆件，108个螺栓球节点连接各个杆件。整个桁架的杆件和节点材料为钢材，弹性模量和密度分别为2.06×1011Pa和7 800 kg/m3，模型如图1所示。

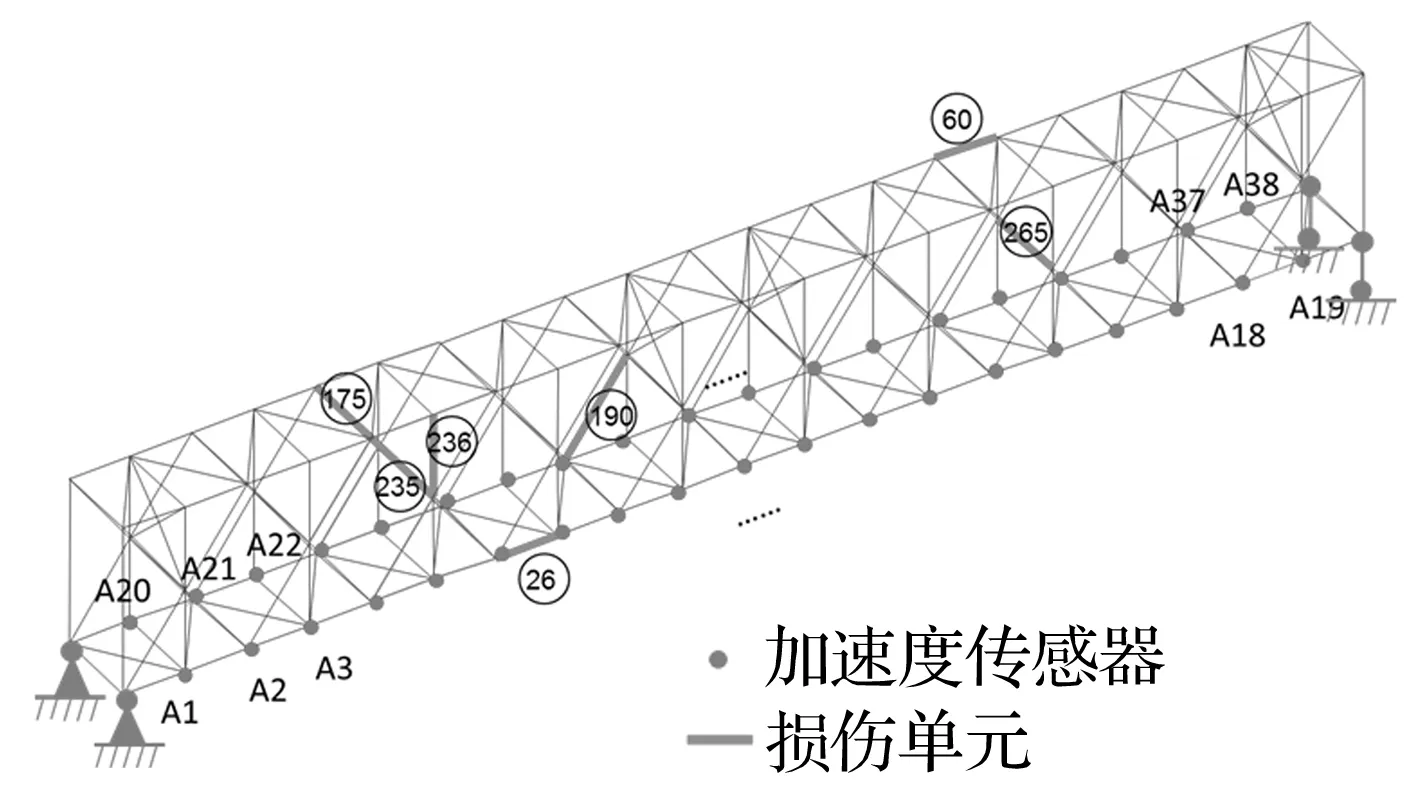
图1　桁架有限元模型Fig.1 Finite element model of truss structure

考虑实际工程结构测点有限的情况，选择测点数为38个，布置位置如图1所示，均为下弦杆节点。取结构的前四阶竖向振型和对应的频率，振型包括前3阶竖向振型与第1阶竖向扭转振型。采用降低单元弹性模量的方法模拟损伤，设置三种损伤工况。损伤工况1为单元235损伤10%；损伤工况2为单元175与236各损伤10%；损伤工况3为单元26，60，175，190，265分别损伤5%，5%，10%，10%，10%。在有限元计算得到的前4阶模态参数上加噪声，模拟实测数据噪声的影响，噪声水平分别为1%，5%与10%。

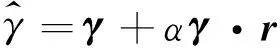
(17)

4.1计算结果

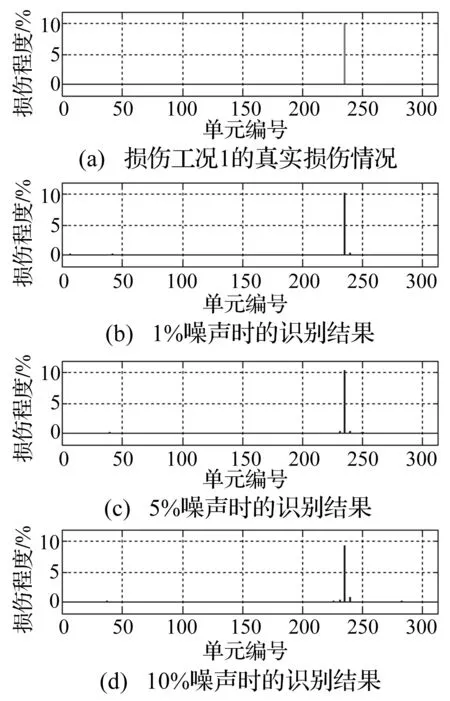
图2　损伤工况1的识别结果Fig.2 Damageidentification results of Case 1

损伤工况1的识别结果如图2所示，图2(a)为真实的损伤情况，图2(b)～(d)为识别结果，从图中看出，对1个单元损伤的工况，损伤识别结果较好，即使在10%的噪声下，也能准确识别损伤位置与损伤程度。

损伤工况2为2个单元的损伤情况，识别结果如图3所示，图3(a)为真实的损伤情况，单元175与236各损伤10%。图3(b)～(d)为识别结果，从图中看出，损伤识别结果较好，但是随着噪声的增加，损伤程度的识别结果准确度降低，但是损伤位置识别较好。

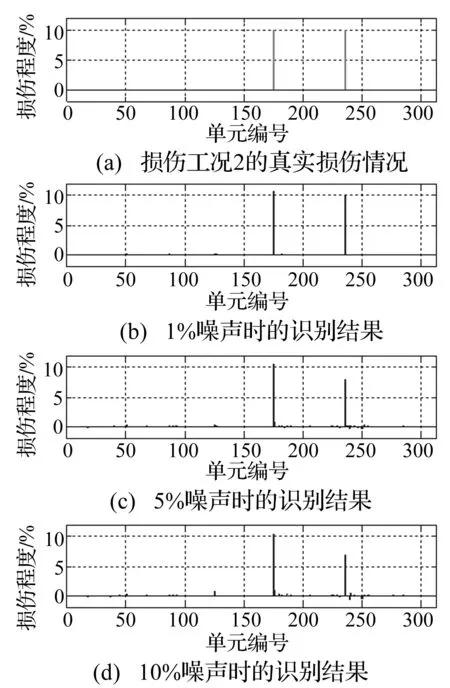
图3　损伤工况2的识别结果Fig.3 Damageidentification results of Case 2

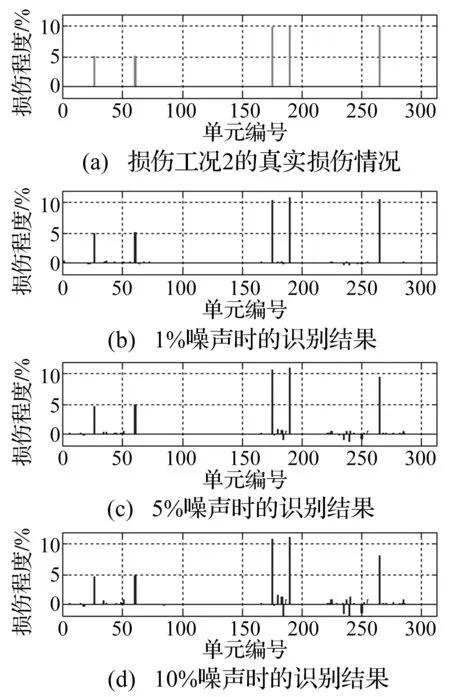
图4　损伤工况3的识别结果Fig.4 Damageidentification results of Case 3

损伤工况3为5个单元的损伤情况，识别结果如图4所示，图4(a)为真实的损伤情况，损伤工况3为单元26，60，175，190，265分别损伤5%，5%，10%，10%，10%。图4(b)～(d)为识别结果，从图中看出，对于多个单元损伤的情况，本文提出的方法仍然可以较准确的识别损伤位置与损伤程度。对于多损伤的情况，随着噪声的增加，损伤程度的识别结果准确性降低。

4.2不考虑稀疏约束的对比结果

对式(15)，不考虑稀疏约束，令λ=0，三种工况的计算结果如图5～7所示。对于工况1，不考虑稀疏约束的情况下可以正确识别损伤情况，但10%噪声时，损伤程度识别结果的准确性降低。对考虑多损伤的工况2和3，均存在误判的情况，且随着噪声的增加，识别结果的准确性进一步降低。从对比结果可以看出，考虑损伤的稀疏性，可以明显增加损伤识别的准确性。

4.3测点数目影响

为研究不同测点数目对识别结果的影响，对测点数[8,10,…,38]的情况分别计算损伤识别结果，识别误差采用下式计算

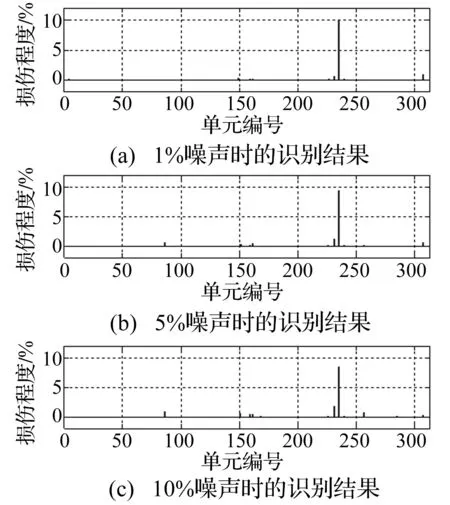
图5　λ=0时，损伤工况1的识别结果Fig.5 Damage identification results of Case 1 with λ=0

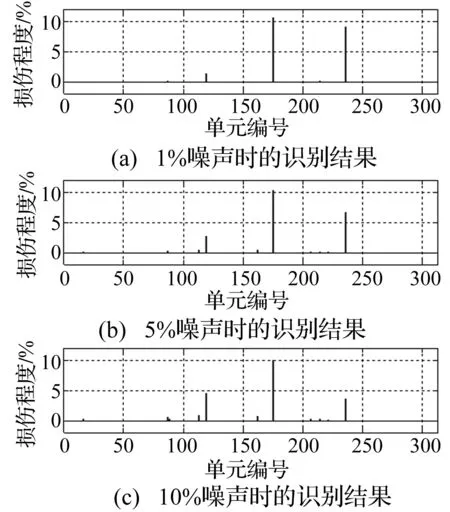
图6　λ=0时，损伤工况2的识别结果Fig.6 Damage identification results of Case 2 with λ=0

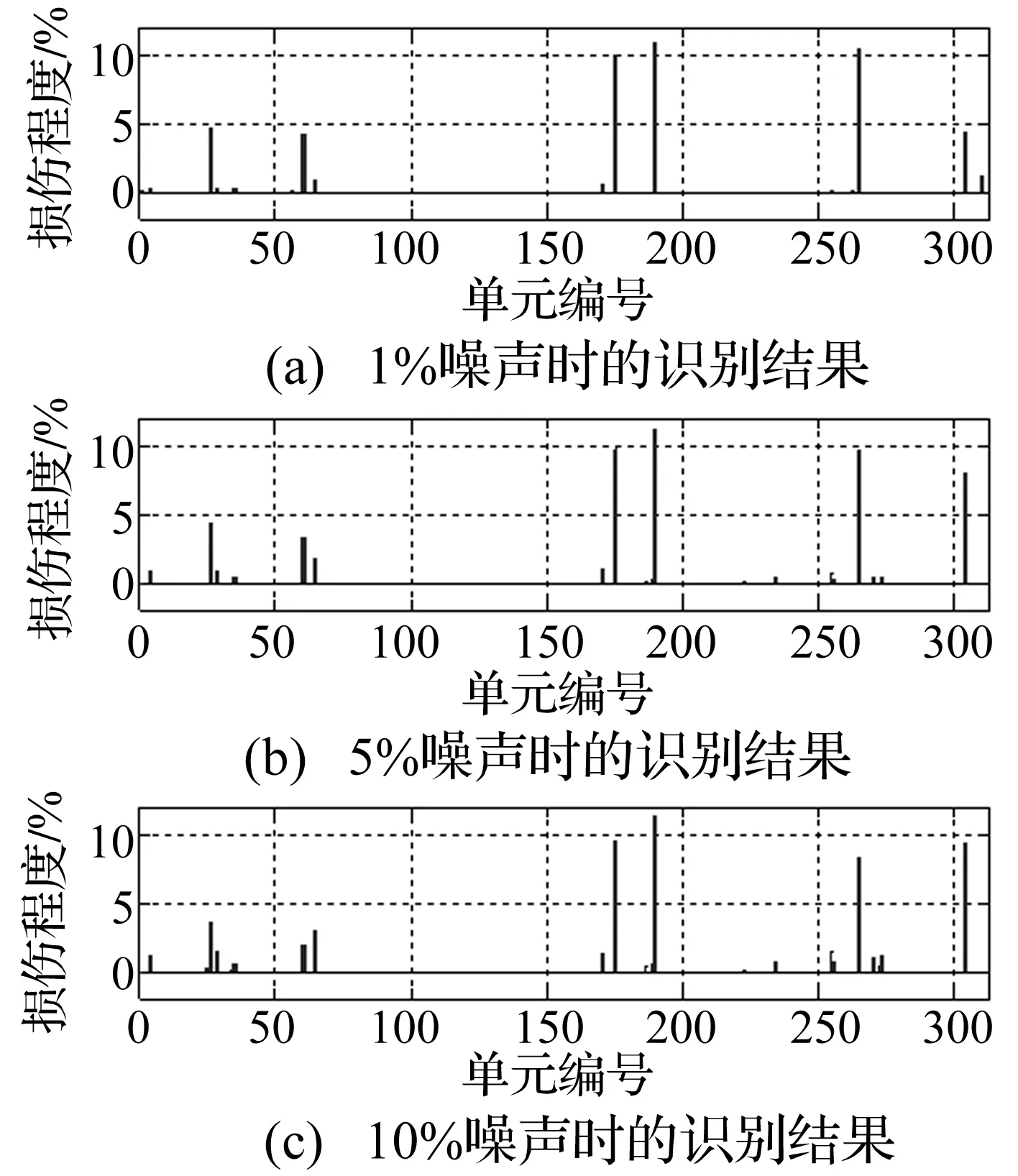
图7　λ=0时， 损伤工况3的识别结果Fig.7 Damage identification results of Case 3 with λ=0

(18)

计算结果如图8所示，从图中可以看出，随着测量点数的增加，识别结果的误差减少，相比于多个损伤的情况，损伤单元越少，误差越小。噪声对识别结果有影响，随着噪声的增加，识别误差增大。

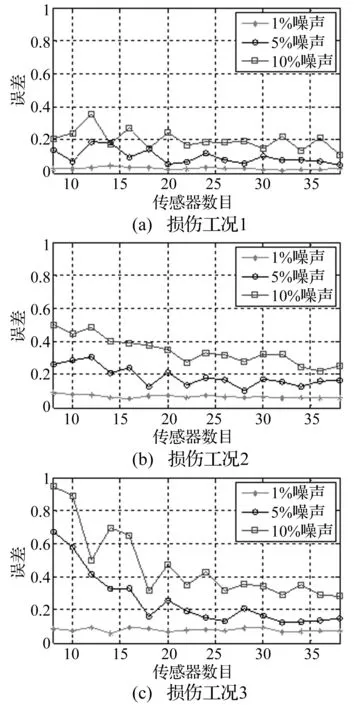
图8　测点数目对识别结果的影响Fig.8 Influence of sensor number to identification error

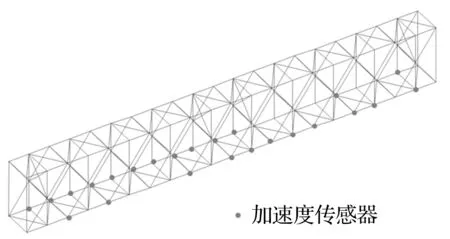
图9　24测点传感器布置位置Fig.9 Placement of 24 sensors

借鉴压缩感知理论中随机采样的思想，这里矩阵Γ取随机矩阵。随机选择24个测点，研究测点布置位置对识别结果的影响。测点位置随机布置如图9所示。

在24个测点下，三种损伤工况在10%噪声水平下的识别结果如图10所示，从图中可以看出，少量测点随机布置的情况下仍然可以得到较好的损伤识别结果。进一步验证了提出的方法的鲁棒性。同时在实际的工程结构监测系统中，布置的某些传感器会在使用过程中损坏或出现数据测量不准的情况，而且损坏的具体传感器难以预测，具有一定的随机性，按照传统的传感器优化布置方法，损坏之后的传感器可能会影响损伤识别结果。但是本文提出的方法，即使少数传感器出现问题，仍然可以取得较好的识别结果。

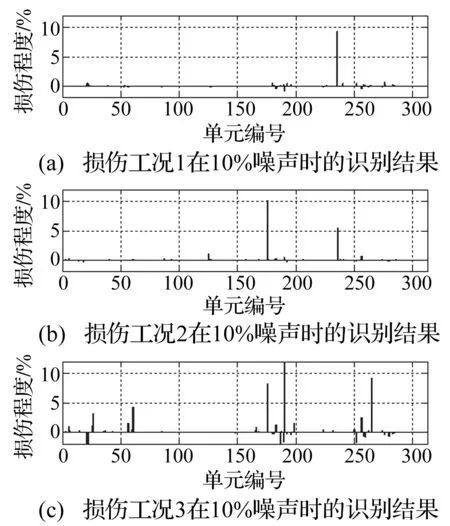
图10　24个测点时的识别结果Fig.10 Damage identification results with 24 test points

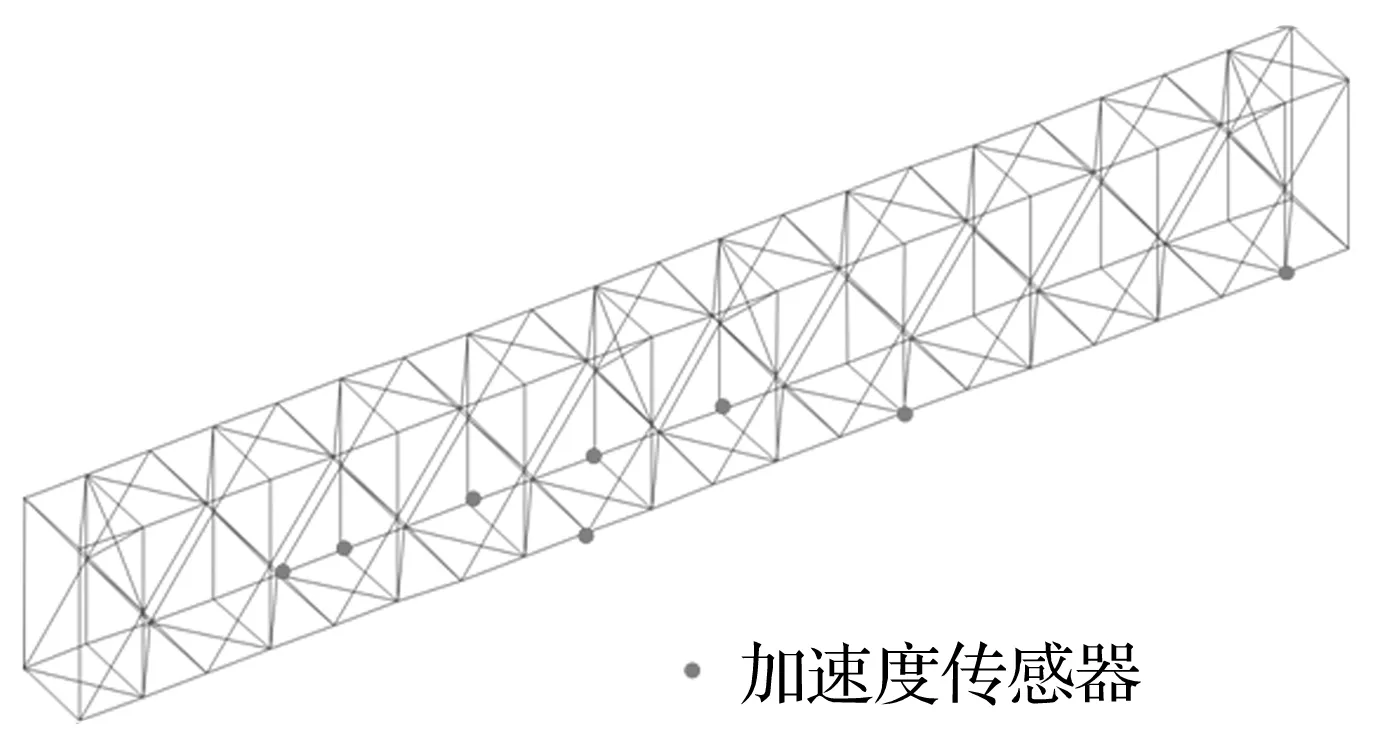
图11　8测点传感器布置位置Fig.11 Placement of 8 sensors

对8个测点的情况，传感器布置如图11所示，识别结果如图12所示。在8个测点时10%噪声情况下，对于工况1，可以较准确的识别，对于工况2和3，识别结果较差。

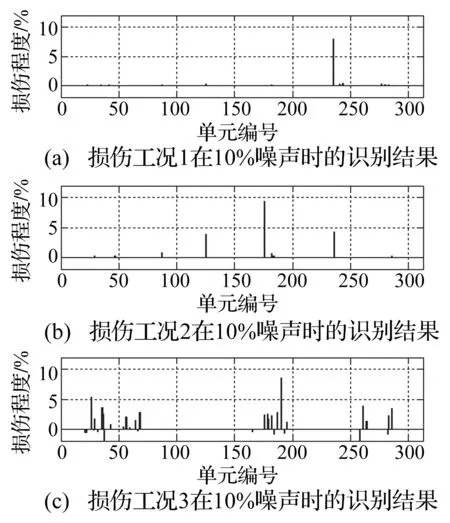
图12　8个测点时的识别结果Fig.12 Damage identification results with 8 test points

5结论

提出了基于结构灵敏度分析与稀疏优化的结构损伤识别方法，该方法在结构损伤稀疏的基础上，通过灵敏度分析，建立结构单元损伤程度与实测频率和振型变化量之间的关系，由于实际测量点的有限以及测试振型的不完备，所建方程为一对噪声敏感的病态线性方程组，传统方法较难获得准确解，本文根据压缩感知理论，引入稀疏约束对方程组进行求解。通过一个简支桁架模型的数值模拟，考虑噪声影响与测点不完备，对方法进行了验证。结果表明：提出的方法可以准确的识别结构损伤，在少量测点下，即使受10%的噪声影响也可以获得较好的损伤识别结果。与不考虑稀疏约束的损伤识别结果对比表明，考虑稀疏约可以明显增加损伤识别的准确性。

参 考 文 献

[1] 欧进萍. 重大工程结构智能传感网络与健康监测系统的研究与应用[J]. 中国科学基金,2005(1):8-12.

OU Jin-ping. Research and practice of smart sensor network and health monitoring systems for civil infrastructures in mainland China[J]. Science Foundation in China,2005(1):8-12.

[2] 李宏男，高东伟，伊廷华. 土木工程结构健康监测系统的研究状况与进展[J]. 力学进展,2008,38(2):151-166.

LI Hong-nan,GAO Dong-wei,YI Ting-hua.Advances in structural health monitoring systems in civil engineering[J]. Advances in Mechanics,2008,38(2):151-166.

[3] 李爱群，丁幼亮，王浩，等. 桥梁健康监测海量数据分析与评估——“结构健康监测”研究进展[J]. 中国科学,2012,42(42):972-984.

LI Ai-qun,DING You-liang,WANG Hao,et al. Analysis and assessment of bridge health monitoring mass data—progress in research/development of “Structural Health Monitoring”[J]. Science China Press,2012,42(42):972-984.

[4] 焦美菊，孙利民，李清富. 基于监测数据的桥梁结构可靠性评估[J]. 同济大学学报:自然科学版,2011,39(10):1452-1457.

JIAO Mei-ju,SUN Li-min,LI Qing-fu. Bridge structural reliability assessment based on health monitoring data[J]. Journal of Tongji University:Natural Science,2011,39(10):1452-1457.

[5] Sohn H,Farrar C R,Hemez F M,et al. A Review of Structural Health Monitoring Literature:1996-2001[R]//LANL Report,LA-13976-MS,2003.

[6] 宗周红，任伟新，阮毅. 土木工程结构损伤诊断研究进展[J]. 土木工程学报,2003,36(5):105-110.

ZONG Zhou-hong,REN Wei-xin,RUAN Yi. Recent advances in research on damagediagnosis for civil engineering structures[J]. China Civil Engineering Journal,2003,36(5):105-110.

[7] 郑栋梁，李中付，华宏星. 结构早期损伤识别技术和发展趋势[J]. 振动与冲击,2002,21(2):1-8.

ZHENG Dong-liang,LI Zhong-fu,HUA Hong-xing. A summary review of structural initial damageidentification methods[J]. Journal of Vibration and Shock,2002,21(2):1-8.

[8] Farrar C R,Baker W E,Bell T M,et al. Dynamic characterization and damage detection in the I-40 bridge over the rio grande [R]. Los Alamos National Laboratory Report,LA-1275. MS. 1994.

[9] Hera A,Hou Z. Application ofwavelet approach for ASCE structural health monitoring benchmark studies[J]. ASCE Journal of Engineering Mechanics,2004,126(7):677-683.

[10] Yang J N,Lei Y,Lin S,et al. Hilbert-Huang based approach for structural damage detection[J]. ASCE Journal of Engineering Mechanics,2004:85-95.

[11] Chen S S,Kim S. Neural network based signal monitoring in a smart structural system[J]. Smart Structures and Materials,1994,2191:175-186.

[12] Balmès E,Basseville M,Mevel L et al. Statistical model-based damage localization:a combined subspace-based and substructuring approach[J]. Structural Control and Health Monitoring,2008,15(6):857-875.

[13] Candès E J. Compressive sampling[C]//Proceedings of the International Congress of Mathematicians,Madrid,Spain,2006:1433-1452.

[14] Candès E J,Romberg J,Tao T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transaction Information Theory,2006,52(2):489-509.

[15] Donoho D. Compressed sensing[J]. IEEE Transaction Information Theory,2006,52(4):1289-306.

[16] 马坚伟，徐杰，鲍跃全，等. 压缩感知及其应用：从稀疏约束到低秩约束优化[J]. 信号处理,2012,28(5):609-624.

MA Jian-wei,XU Jie,BAO Yue-quan,et al. Compressive sensing and its application:from sparse to low-rank regularized optimization[J]. Signal Processing,2012,28(5):609-623.

[17] Zhao J,DeWolf J T. Sensitivity study for vibrational parameters used in damage detection[J]. Journal of Structure Engineering,1999,125(4):410-416.

[18] Boyd S P,Vandenberghe L. Convex optimization[M]. Cambridge University Press,Cambridge,U K,2004

Structural damage identification based on structural sensitivity analysis and sparse restrains optimization

ZHOU Shu-mei, BAO Yue-quan, LI Hui

(School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China)

Abstract:Sparse constraints are now very popular to solve inverse problems in the field of applied mathematics. Structural damage identification is a typical inverse problem of structural dynamics; structural damage is a spatial sparse phenomenon, i.e., when structural damage occurs, only part of elements or substructures are damaged. Here, a structural damage identification method based on the structural sensitivity analysis and the sparse constraints optimization was proposed. Based on the structural sensitivity analysis, the linear equations for structural damage stiffness parameter variations and changes of modal parameters were established. Considering the structural damage sparsity conditions, the sparse constraints optimization method was employed to solve the equations. The numerical example of a truss structure considering measurement noise, incompleteness of measurements and multi-damage cases was simulated. The effects of sensor number and layout on the identification results were also investigated. The results indicated that the damage locations and levels can be effectively identified with the proposed method; considering sparse constraints, the accuracy of structural damage identification is obviously improved.

Key words:structural health monitoring; structural damage identification; compressive perception; structural sensitivity analysis; sparse restrains optimization

基金项目：973计划课题(2013CB036305)；国家自然科学基金面上项目(51738154)

收稿日期：2015-02-09修改稿收到日期：2015-05-05

通信作者鲍跃全 男，博士，副教授，1981年6月生

中图分类号:TU317; TU392.5

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.021

第一作者 周述美 男，博士生，1982年12月生

E-mail: baoyuequan@hit.edu.cn