浅谈《数字信号处理》实践教学
肖驰


摘要:现阶段本科院校主要以培养应用型人才。应用型集中体现技术应用能力,这就要求根据“宽口径,厚基础,强能力”的原则构建理论教学体系。《数字信号处理》是面向电子信息学科的专业基础课,它的基本概念、基本分析方法已经渗透到了各个领域。为了提高学生的实践能力,采用“工程化”实践教学体系。通过实践教学,提高了学生的创新能力和培养工程意识。
关键词:应用型人才;工程化教学;压缩感知;信号处理
中图分类号:G424 文献标识码:A 文章编号:1009-3044(2016)03-0157-02
1 概述
随着我国高等教育大众化的快速发展和社会需求变化,普通本科院校转变思路,将人才培养目标定位于应用型本科教育,为经济社会发展培养应用型人才的发展道路上来。应用型人才主要强调能力的培养,既要有复合型,即实现技术交叉、应用交叉以及技术应用的交叉,还要外向型,主要适应工程环境的能力。故各门学科的教学就要以提高能力为出发点,深化改革,建立培养应用型人才的新模式。“工程化”教育不仅要向学生传授现代化的科技知识,更应该在知识的传授过程中渗透工程技术的内容,使之体会和掌握工程设计、工程实践的一般规律和基本分析方法,避免学院教学理论化的脱离实际的倾向。
近年来计算机和信息技术的快速发展,电子信息和计算机学科之间的交叉联系越来越广,当前许多新兴领域综合多学科的知识。例如物联网综合传感、嵌入式、网络通信和信号处理技术。专业界限淡化和学科互相渗透的特点迫使学生掌握一定的知识和技能,只有这样才能提高学生的综合素质和社会适应能力。
2实例教学
本文以压缩感知为载体,采用工程化实践教学,培养工程意识,提高学生综合能力!对于学生来说,采样理论就是奈奎斯特定理。而压缩传感。它作为一个新的采样理论,对于学生来说是很陌生的。如何能让学生理解,并使用是一个难题。采用工程案例教学,全方位地模拟真实项目案例。
2.1压缩感知简介
传统的采样要求:[fsampling≥2fmax] ,而压缩感知是在远小于Nyquist 采样率的条件下,通过随机采样获取信号的离散样本,运用非线性重建算法重建信号。压缩感知理论一经提出,就引起学术界和工业界的广泛关注。
对于初始信号[x∈C(N*1)] ,传统压缩是构造正交矩阵[A∈C(N*N)] ,正变换得到[y=Ax],逆变换为[x=A-1y] 。传统压缩就是构造正交阵进行编解码,将所有信号全部存储下来。
而压缩感知理论主要利用信号在某个域的稀疏性。只要信号是可压缩的或在某个变换域是稀疏的,就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上,再求解一个优化问题就得到从这些少量的投影中重构出原信号。
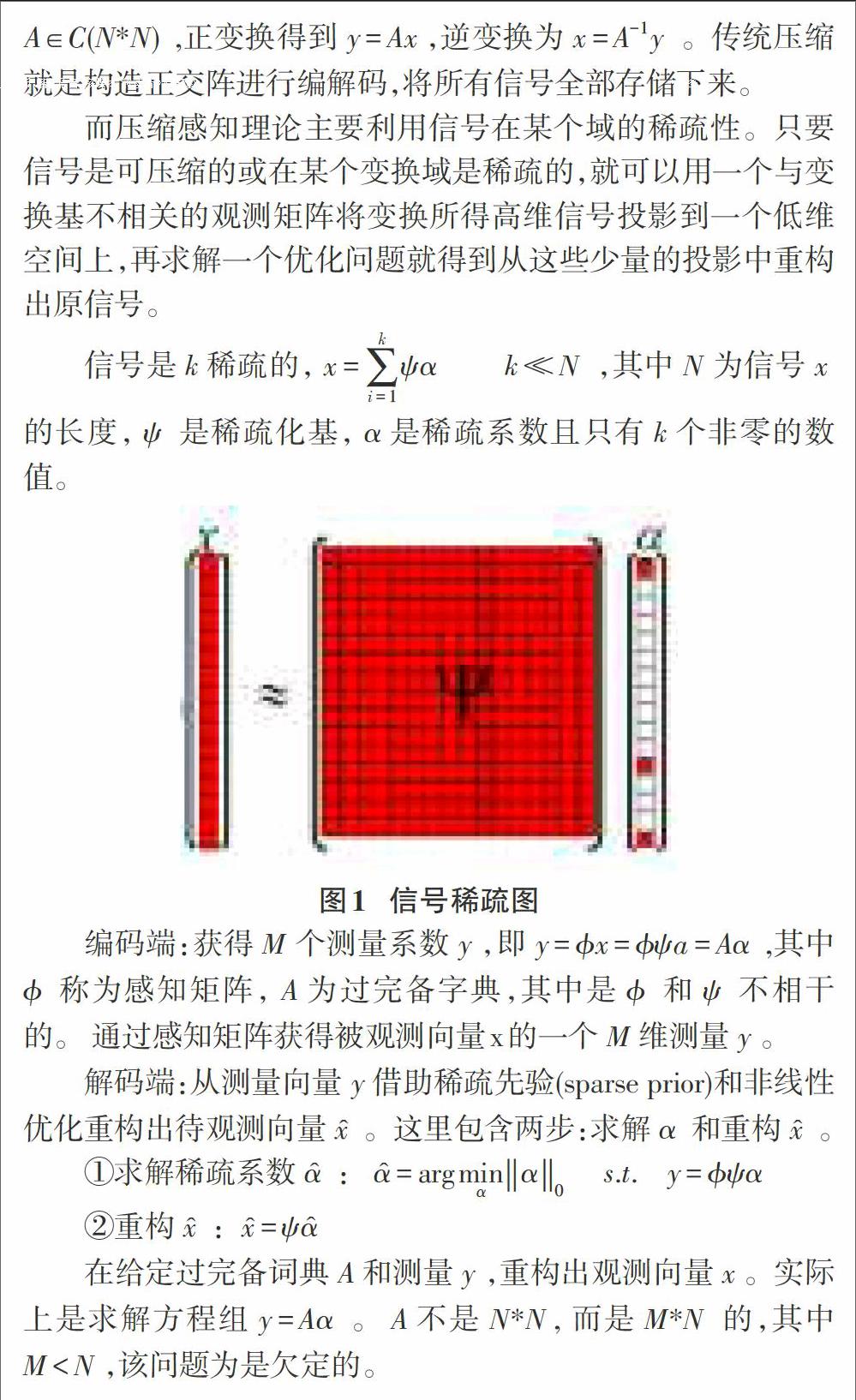
信号是[k]稀疏的,[x=i=1kψα?k?N] ,其中[N]为信号[x] 的长度,[ψ] 是稀疏化基,[α]是稀疏系数且只有[k]个非零的数值。
编码端:获得[M]个测量系数[y],即[y=?x=?ψa=Aα] ,其中[?] 称为感知矩阵,[A]为过完备字典,其中是[?] 和[ψ] 不相干的。 通过感知矩阵获得被观测向量x的一个[M]维测量[y]。
解码端:从测量向量[y]借助稀疏先验(sparse prior)和非线性优化重构出待观测向量[x] 。这里包含两步:求解[α] 和重构[x] 。
①求解稀疏系数[α] : [α=argminαα0s.t.y=?ψα]
②重构[x] : [x=ψα]
在给定过完备词典[A]和测量[y],重构出观测向量[x]。实际上是求解方程组[y=Aα] 。[A]不是[N*N], 而是[M*N] 的,其中[M 2.2工程实例及算法 在这个工程中要求学生有算法分析能力和一定编程能力,隐含的是学生的数学建模能力。 用一个包含3个频率的1维信号实例教学,三个频率为f1=50、f2=100和f3=400;采样频率为fs=800;t采样间隔为s=1/fs;采样序列为Ts=1:N;x为1维信号。 x=0.2*cos(2*pi*f1*Ts*ts)+0.9*cos(2*pi*f2*Ts*ts)+0.5*cos(2*pi*f3*Ts*ts) 本文信号的压缩重建采用了正交匹配追踪法(Orthogonal Matching Pursuit),该算法的基本思想是在每一次的迭代过程中,从过完备原子库里选择与信号最匹配的原子来进行稀疏逼近并求出余量,然后选出与信号余量最为匹配的原子。经过数次迭代,该信号就可以由原子线性表示。 算法符号描述[rt] 表示残差,[t] 表示迭代次数,[Λt] 表示[t] 次迭代的索引集合,[λt] 表示[t] 次迭代找到的索引,[aj] 表示矩阵[A] 的第[j] 列,[At] 表示按索引[Λt]选出矩阵[A]的列集合。 算法步骤: 1) 初始余量[r0=y] ,迭代次数[t=1] ,索引值集合[Λ0=?] ,[A0=?] 2) 计算[λt=argmaxj=1,...,Nrt-1,aj] 3) 更新支撑集,[Λt=Λt-1?{λt},Αt=Αt-1?aλj] 4) 由最小二乘法得到:[xt=(ATtAt)-1ATty] 5) 更新残差[rt=y-Atxt] 6) 若[rt-r0≥ε,?r=rt,t=t+1] ,转2,否则,停止迭代。 3结束语 通过1维信号的压缩重建,知识点有信号的正变换和逆变换、正交矩阵的构建、贪婪算法、语言编程等。在任务实施中,提高学生所学知识的运用能力和创新能力。学生从整个工程中,学到了课本中没有的内容,即工程意识和团结协作等。 应用型人才的培养主要体现在知识、能力、素质的培养。课堂上教学主要是传授知识和引导学生。学生通过对新理论知识的学习,在工程实训中掌握它并应用于技术创新中。能力的培养不是通过一门课程来培养这些素质,而应隐含这个任务于各门课程教学中。可以培养出学生有创新能力,在择业竞争中出于有利地位。 参考文献: [1] 焦李成,杨淑媛,刘芳,等. 压缩感知回顾与展望[J].电子学报,2012,39(7):1651-1662. [2] Joel A. Tropp and Anna C. Gilbert. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit[J]. IEEETransactions on Information Theory, VOL. 53, NO. 12, DECEMBER 2007. [3] 沙威.CS_OMP,http://www.eee.hku.hk/~wsha/Freecode/Files/CS_OMP.zip [4] 奥本海姆信号与系统[M].电子工业出版社,2013.

