气液两相流问题的高精度数值模拟

覃柏英， 林贤坤， 荣吉利， 冯志伟

(1. 广西科技大学 理学院，柳州　545006; 2. 广西科技大学 汽车与交通学院，柳州　545006;3. 北京理工大学 宇航学院，北京　100081)

气液两相流问题的高精度数值模拟

覃柏英1， 林贤坤2， 荣吉利3， 冯志伟3

(1. 广西科技大学 理学院，柳州545006; 2. 广西科技大学 汽车与交通学院，柳州545006;3. 北京理工大学 宇航学院，北京100081)

摘要：采用加权三阶ENN格式离散Euler方程、LS运输方程及其重新初始化方程的空间导数，耦合三阶Runge-Kutta法离散它们的时间导数，LS法追踪运动界面和MGFM 法定义界面边界条件，探讨了气液两相流问题的高精度数值模拟。通过一维大密度大压力比实验的数值模拟，以及二维水下爆炸过程中冲击波的产生、传播、反射、透射和水面隆起等演化过程的数值模拟，验证了该方法的可行性和稳定性，可实现气液两相流的高精度数值模拟及其运动界面的高分辨率追踪。

关键词：气液两相流；ENN格式；WENN格式；Level Set法；MGFM 法；界面追踪

因气液两种介质可压缩性、密度、压力等存在巨大差异，气液两相流的数值模拟一直是可压缩多介质流数值模拟的难点和热点，其研究重点是运动界面的精确追踪和界面边界条件的稳健构造。对于运动界面的追踪，目前主要有波前追踪(Front Tracking)[1]和界面捕捉(Front Capturing)[2]两大类方法。前者难于处理发生拓扑变化的界面，且拓展到高维时算法非常复杂，后者计算简单，格式统一，易于处理界面的拓扑变化。而对于界面边界条件的构造，因界面两侧流体具有完全不同的特性，密度、速度和压力在界面处都有可能出现大梯度变化，传统方法难以实现稳健的构造。

作为界面捕捉法其中一种的Level Set(LS)法[3]，可处理复杂和发生拓扑变形的运动界面，且其特征隐含于LS函数，可较精确描述运动界面。基于LS法，Fedkiw等[4]引入Ghost Fluid Method(GFM)，通过界面边界条件定义，将多介质流动问题转化为单介质流问题进行求解。但GFM未考虑到界面两侧流体的性质及相互作用，计算强激波与界面作用问题时出现数值振荡。刘铁钢等[5]通过界面处Riemann 问题的构造和求解，由其解定义界面边界条件，得到引入了较小守恒误差的Modified Ghost Fluid Method(MGFM)，从而能准确计算界面处流体状态出现大梯度变化的问题。

对可压缩多介质流的数值模拟，目前已发展了WENO、NND格式和RKDG有限元法等[6-11]，其中无振荡无自由参数耗散的NND格式，具有物理概念清楚，差分格式简单，易于编程和计算量小等优点。为了提高精度，在NND基础上，张涵信等[12]推导出精度达三阶的ENN格式(ENN3)。

为了进一步提高ENN3的精度，采用加权方法，可获得加权ENN3格式(WENN3)，本文通过实例对其精度进行分析。同时，采用WENN3离散气液两相流的Euler方程、LS方程及其重新初始化方程的空间导数，三阶Runge-Kutta法离散时间导数，耦合LS法追踪运动界面和MGFM法定义界面边界条件，对气液两相流的高精度数值模拟和运动界面的高分辨率追踪进行探讨和研究。

1基本方程

1.1Euler方程组

二维可压缩流体力学Euler方程组为

(1)

式中，U=[ρ，ρu，ρv,E]T，F=[ρu，ρu2+p，ρuv,u(E+p)]T，G=[ρv，ρuv,ρu2+p，v(E+p)]T。ρ,u,v,E,p分别为密度、x和y方向速度、能量和压力。

采用Stiffened状态方程描述气液两种流体，则

p=(γ-1)ρe-γπ

(2)

式中,e为内能，π为具有黏性张量量纲的常数，γ对气体为比热比，液体为拟合常数。不同流体γ和π有确定值。理想气体γ=1.4,π=0，水γ=7.15,π=3 309。

1.2LS方程及其重新初始化方程

在计算区域Ω中，气液分别在区域Ω1和Ω2，气液交界面为∑。设d为t时刻Ω中的点x到∑的距离，则可定义LS函数φ(x,t)为[13]：当x∈Ω1时，φ(x,t)=-d；当x∈∑时，φ(x,t)=0；当x∈Ω5时，φ(x,t)=d。设u,v是流体x和y方向速度，则φ(x,t)满足

(3)

因数值方法的耗散效应，经几个时间步长的迭代后，φ(x,t)不再满足是x点到界面的符号距离，需重新初始化，可求解如下重新初始化方程到稳定解来实现：

(4)

1.3二维转化为一维问题求解

对于二维Euler方程组(1)和方程(3)，可采时间分裂法求解，即将其分裂成两个一维问题分别求解：

(5)

(6)

由Un，利用式(5)的第一式可求出Un+1/2；再由Un+1/2，利用第二式可求出Un+1。由φn，利用式(6)的第一式可求出φn+1/2；再由φn+1/2，利用第二式可求出φn+1。

对于二维重新初始化方程(4)，将按下式进行求解：

(7)

式中,φy的求解类似于φx，方程(7)的求解类似于一维。

2WENN3有限差分法

2.1算法理论

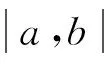
已知函数f(x)在各网格中心xi的函数值f(xi)，设Δfi+k+1/2=fi+k+1-fi+k，k=-2,-1,0,1，函数f(x)在右边界xi+1/2的左状态值由ENN3计算[15]：

(8a)

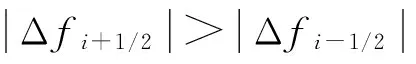
(8b)

其中式(8a)和(8b)中等号右边的第三部分，都选择绝对值最小的项。从而

(9)

为了提高精度，对ENN3引入加权思想，构造加权三阶ENN有限差分法(WENN3)，即设[16]

(10)

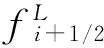
(11)

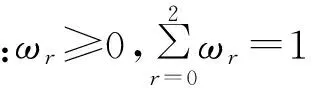
(12)

式中，为了避免分母为零，取ε=10-6。dr为线性权，βr为光滑因子：

2.2精度分析

(14)

表1　ENN3和WENN3的误差与精度

由表1可知，ENN3的精度只有三阶，而WENN3的精度可达五阶。因此，相比ENN3，WENN3的精度得到了提高，更适合气液两相流的高精度数值模拟及其运动界面的高分辨率追踪。

3改进GFM法(MGFM)

(15)

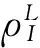
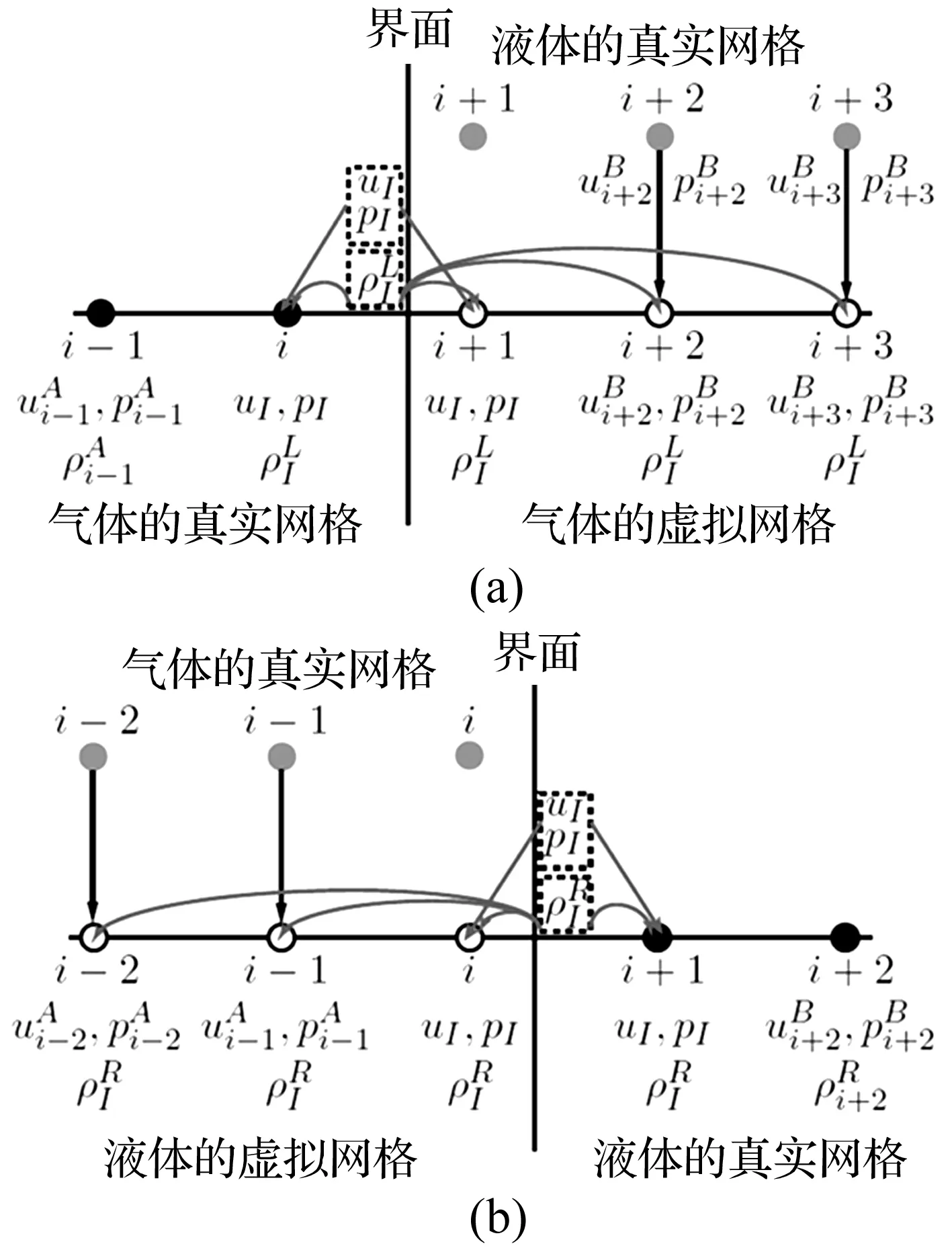
图1　采用MGFM 对气体各网格的密度、速度和压力赋值Fig. 1 The grid unit and method to compute normal vector

4数值模拟

对于一维问题的Euler方程组(5)、LS方程(6)及其重新初始化方程(4)，其空间导数可采用ENN3或WENN3求解，时间导数可采用三阶Runge-Kutta法提高精度。现给出求解空间导数的具体思路与方法。

4.1Euler方程组的求解

(16)

对∂F+/∂x,∂F-/∂x进行空间离散，有

(17)

(18)

4.2LS方程的求解

对方程(6)采用冻结系数法，并对∂φ/∂x空间离散，有

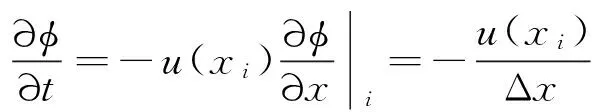
(19)

4.3LS值的重新初始化

将一维重新初始化方程(4)写成如下形式：

(20)

(21)

(22)

5数值实验

5.1一维算例

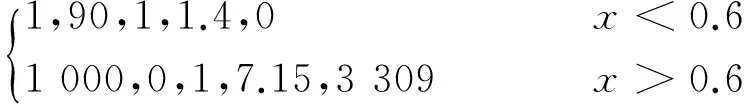
算例1的密度比为1 000，算例2的压力比为8 000，算例3的密度比和压力比都为1 000，分别为大密度比大压力比的气液两相流问题。取网格数为N=500，计算时间分别为T=0,1,0.015,0.001 9,0.02，条件数为CFL=0.1，3个算例的密度、速度和压力分布如图2～图4所示。

图2　算例1的密度、速度和压力分布图Fig.2 The distribution of density, velocity and pressure of first example

图3　算例2的密度、速度和压力分布图Fig.3 The distribution of density, velocity and pressure of second example

图4　算例3的密度、速度和压力分布图Fig.4 The distribution of density, velocity and pressure of third example

由图2～图4可见冲击波、稀疏波和接触间断。相对于ENN3，WENN3的密度、速度和压力的数值解与精确解的吻合度很高，在接触间断左右侧未出现非物理振荡，且接触间断的耗散宽度和运动界面宽度被控制在4个网格内。对于ENN3，算例4和6速度的数值解与其精确解不吻合，同时，算例6的压力也不吻合。

5.2二维算例

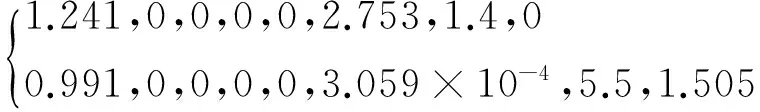
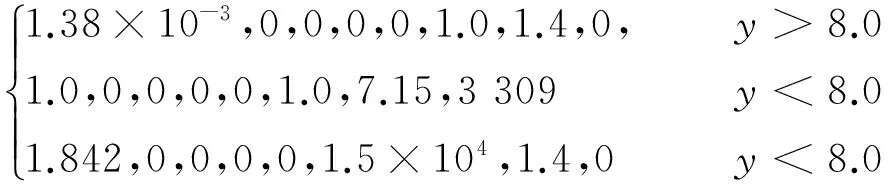
算例4来自文献[17]，算例5和6来自文献[6]。算例4为大压力比气液两相流问题，气液压力比近9 000。算例5和6分别是深水和近水面爆炸问题，数值模拟水中炸药爆炸时产生的爆轰产物，即高压气体与周围水的相互作用。两个算例都存在大压力比，高压气体与水压力比为15 000。同时，算例6还存在大密度比，空气与水密度比达720多。取网格数为N=300×300，条件数为CFL=0.25，由初始界面开始，三个算例运动界面变化如图5所示，其中界面间相隔50个时间步长。不同时刻的密度、压力等值线分别如图6～图9所示。

图5　三个算例的运动界面变化图Fig. 5 The moving interface changes of three examples

(a) T=0.017 985 0　　　　　(b) T=0.037 994 1　　　　　　(c) T=0.057 989 3　　　　　　(d) T=0.077 500 0图7　算例4不同时刻的压力分布图Fig.7 The pressure distribution in different time of four example

(a) T=0.002 360 7　　　　　(b) T=0.004 820 2　　　　　　(c) T=0.007 508 1　　　　　　(d) T=0.009 787 4图8　算例5不同时刻的密度分布图Fig.8 The density distribution in different time of fifth example

(a) T=0.002 360 7　　　　　(b) T=0.004 820 2　　　　　　(c) T=0.007 508 1　　　　　　(d) T=0.009 787 4图9　算例5不同时刻的压力分布图Fig.9 The pressure distribution in different time of fifth example

从图6～图9可看出，高压气体向外膨胀过程中压缩其周围液体，产生向外传播的冲击波，并将大部分能量转化为冲击波能量，同时在气液交界面处产生向内传播的稀疏波。随着高压气体能量的转化，其能量迅速衰减，冲击波接收的能量也迅速减少，当气液压力接近时，冲击波不再接收气体能量，开始脱离气体独立向外传播。气液交界面在高压气体作用下继续向外膨胀过程中，由于冲击波向外传播速度快，致使两者间距离逐渐增加。从算例4结果可见，在近相同时刻T=0.057 989 3，本文结果与文献[17]结果相符合。同时，由算例5结果可见，在近相同时刻T=0.002 360 7，T=0.004 820 2和T=0.009 787 4，本文结果与文献[6]结果相符合。结果在接触间断处仍然存在振荡，可能是MGFM在定义界面边界条件引入的误差导致，但相比文献结果，振荡明显减小。因此，本文方法较准确模拟了深水的水下爆炸过程，及其冲击波的产生和传播。

从密度和压力分布图10和11可看出，对于近水面爆炸问题的算例6，在T=0.003 680 7前，高压气体也是向外膨胀过程中压缩其周围水，产生向外传播的冲击波，同时在气液交界面处产生向内传播的稀疏波。之后如T=0.004 874 4时，冲击波与空水交界面发生相互作用，导致空水交界面开始向上运动，同时在空水交界面处产生反射波和透射波。之后如、T=0.008 654 4时，空水交界面处产生的反射波向下传播到气液交界面处，与气液交界面发生相互作用，产生反射波和透射波，透射波传入气体中，反射波向上运动，与气液交界面作用，使其加速向上运动；之后如T=0.013 118 3时，因冲击波在空水交界面和气液交界面间不断反射，使得气液交界面和空水交界面间的距离逐渐减小，并且水面不断向上隆起。从图10可见，在近相同时刻，本文结果与文献[6]结果相符合。计算结果在接触间断处也仍然存在振荡，这也可能是MGFM定义界面边界条件引入的误差导致，但相比文献[6]的结果，振荡也明显减小。因此，本文方法较准确模拟了近水面爆炸的过程，及其中冲击波的产生、传播、反射、透射和水面隆起等演化过程。

(a) T=0.003 680 7　　　　　(b) T=0.004 847 4　　　　　　(c) T=0.008 654 4　　　　　　(d) T=0.013 118 3图10　算例6不同时刻的密度分布图Fig.10 The density distribution in different time of sixth example

(a) T=0.003 680 7　　　　　(b) T=0.004 847 4　　　　　　(c) T=0.008 654 4　　　　　　(d) T=0.013 118 3图11　算例6不同时刻的压力分布图Fig.11 The pressure distribution in different time of sixth example

6结论

本文对ENN3采用加权方法，获得WENN3，通过实例对两者精度进行分析，明确ENN3的精度只有三阶，而WENN3的精度可达到五阶。采用WENN3离散Euler方程、LS运输方程及重新初始化方程的空间导数，耦合三阶Runge-Kutta法离散其时间导数，LS法追踪运动界面和MGFM 法定义界面边界条件，通过大密度大压力比的数值实验，探讨了气液两相流问题的高精度数值模拟。算例表明，采用MGFM法定义界面边界条件，能较准确计算界面处流体状态出现的大梯度变化，而采用LS法，可较精确描述运动界面的变化，实现运动界面的高分辨率追踪。同时，WENN3保持ENN3优点的同时精度也得到提高，能够很好抑制界面处的非物理振荡，实现气液两相流的高精度数值模拟。数值模拟结果验证了本文方法的可行性和稳定性，较真实模拟了二维水下爆炸过程中冲击波的产生、传播、反射、透射和水面隆起等演化过程，可实现气液两相流的高精度数值模拟及其运动界面的高分辨率追踪，较好抑制了运动界面处的非物理振荡。

参 考 文 献

[1] Marshall G. A front tracking method for one-dimensional moving boundary problems[J].SIAM Journal on Scientific Computing,1986,7(1):252-263.

[2] Osher S,Sethian J A. Fronts propagating with curvature dependent speed:Algorithms based on Hamilton-Jacobi formulations. Journal of Computational Physics,1988,79(1):12-49.

[3] Koren B,Lewis M R,van Brummelen E H,et al. Riemann-problem and level-set approaches for homentropic two-fluid flow computations[J]. Journal of Computational Physics,2002,181:654-674.

[4] Fedkiw R P,Aslam T,Merriman B,et al. A non-oscillatory Eulerian approach to interfaces in multimaterial flows(the ghost gluid method)[J]. Journal of Computational Physics,1999,152(2):457-492.

[5] Liu T G,Khoo B C,Yeo K S. Ghost fluid method for strong shock impacting on material interface[J]. Journal of Computational Physics,2003,190(2)：651-681.

[6] 赵海涛,王成,宁建国. 可压缩多介质问题的高精度数值模拟[J]. 高压物理学报,2013(2):261-267.

ZHAO Hai-tao,WANG Cheng,NING Jian-guo. High resolution of compressible multi-medium flow[J].Chinese Journal of High Pressure Physics,2013(2):261-267.

[7] Gryngarten L D,Menon S. A generalized approach for sub-and super-critical flows using the Local Discontinuous Galerkin method[J]. Computer Methods in Applied Mechanics and Engineering,2013,253(1):169-185.

[8] Zhu Jun,Liu Tie-gang,Qiu Jian-xian,et al. RKDG methods with WENO limiters for unsteady cavitating flow[J].Computers and Fluids,2012,57(30):52-65.

[9] Wang Chun-wu,Shu Chi-wang. An interface treating technique for compressible multi-medium flow with Runge-Kutta discontinuous Galerkin method[J]. Journal of Computational Physics,2010,229(23):8823-8843.

[10] Zhu Jun,Qiu Jian-xian,Liu Tie-gang,et al. RKDG methods with WENO type limiters and conservative interfacial procedure for one-dimensional compressible multi-medium flow simulations[J]. Applied Numerical Mathematics,2011,61:554-580.

[11] 魏海鹏,符松. 不同多相流模型在航行体出水流场数值模拟中的应用[J]. 振动与冲击,2015,34(4):48-52.

WEI Hai-peng,FU Song. Multiphase models for flow field numerical simulation of a vehicle rising from water[J]. Journal of Vibration and Shock,2015,34(4):48-52.

[12] 张涵信,贺国宏,张雷. 高精度差分求解气动方程的几个问题[J]. 空气动力学学报,1993(4):347-356.

ZHANG Han-xin,HE Guo-hong,ZHANG Lei. Some important for high order accurate difference solving gas dynamics equations[J]. Acta Aerodynamica Sinica,1993(4):347-356.

[13] Shen Yi-qing,Wang Ru-quan. A fifth-order accurate weighted ENN difference scheme[J]. Communications in Nonlinear Science and Numerical Simulation,1997(2):111-116.

[14] 陈荣三,蔚喜军. 二维多介质可压缩流的RKDG有限元方法[J]. 计算物理,2006(6):699-705.

CHEN Rong-san,YU Xi-jun. An RKDG finite element method for Two-dimensional compressible multi-media fluids[J]. Chinese Journal of Computational Physics,2006(6):699-705.

High precision numerical simulation for gas-liquid two-phase flow

QIN Bo-ying1, LIN Xian-kun2, RONG Ji-li3, FENG Zhi-wei3

(1. College of Science, Guangxi University of Science and Technology, Liuzhou 545006, China;2. College of Automobile and Transportation Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China;3. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)

Abstract:Coupled with the third-order Runge-Kutta, LS and modified ghost fluid method MGFM, the weighted ENN3 scheme (WENN3) was proposed to study the numerical simulation for gas-liquid two-phase flow. WENN3 was applied to discrete the spatial derivative of Euler equation, level set (LS) transport equation and its reinitialization equation. The third-order Runge-Kutta was applied to discrete their time derivative. LS method was applied to track the moving interface and MGFM method was applied to define interface boundary conditions. Through one-dimensional simulations with high density and high pressure ratio, and two-dimensional underwater explosion simulations, the evolution process of shock wave generation, propagation, reflection, transmission and water surface uplift were analyzed, the numerical simulation for gas-liquid two-phase flow were performed, and the correctness and reliability of the proposed method were verified. The results of numerical simulations showed that this method has high resolution, high precision, and many advantages in suimulating gas-liquid two-phase flow with high density, high pressure ratio and strong discontinuity, and it can realize high resolution tracking of moving interface.

Key words:gas-liquid two-phase flow; ENN3; WENN3; level set (LS) method; MGFM; moving interface tracking

基金项目：国家自然科学基金项目(51209042;1272057)

收稿日期：2014-12-16修改稿收到日期：2015-04-27

通信作者林贤坤 男，博士，教授，1976年生

中图分类号:O354;O368;O382

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.013

第一作者 覃柏英 女，硕士，讲师，1979年生

E-mail:Linxk0209@163.com