复杂转子-轴承-汽封耦合系统的非线性振动分析

袁铭鸿， 童水光,， 从飞云， 李发宗

(1. 浙江大学 热工与动力系统研究所，杭州　310027； 2.浙江大学 机械设计研究所，杭州　310027)

复杂转子-轴承-汽封耦合系统的非线性振动分析

袁铭鸿1， 童水光1,2， 从飞云2， 李发宗1

(1. 浙江大学 热工与动力系统研究所，杭州310027； 2.浙江大学 机械设计研究所，杭州310027)

摘要：基于非线性动力学和转子动力学理论，综合考虑Muszynska非线性汽封力、非线性油膜力和转子不平衡量的耦合作用，建立了双叶轮-轴承交错布置的复杂转子-轴承-汽封系统动力学模型。采用有限元法(FEM)推导系统运动微分方程，编程计算了系统转速、圆盘偏心量、汽封长度和汽封间隙等参数对系统动力特性的影响，并利用分岔图、频谱图、相轨迹和Poincare映射图表征了系统的运动性态。研究表明：耦合系统具有高度非线性，随着参数的变化系统呈现出周期运动、倍周期运动、准周期运动和混沌运动等复杂动力学行为。通过减小圆盘偏心，增加系统汽封长度，选取合适的汽封间隙有利于提高转子-轴承-汽封系统的稳定性，改善系统的运动特性。

关键词：非线性振动；转子动力学；有限元法；分岔；混沌

在旋转机械转子系统中，非线性动力学问题一直是国内外学者研究的热点[1-3]。叶顶间隙汽封力、滑动轴承油膜力、迷宫密封力，以及裂纹和碰摩等引起的非线性力是影响整个系统稳定性的重要因素之一[4-5]。随着机组向高转速大容量等大型化高参数的结构发展，研究转子系统动态响应和稳定性是关系到机组安全生产、可靠运行的重要课题。文献[6-7]经过大量实验提出一种非线性流体密封模型(Muszynska模型)，采用流体周向平均流速比表征流体运动，正确表征了汽封力的非线性特性。文献[8]基于哈密尔顿原理和有限元法建立了一个简单的转子系统模型，考虑非线性汽封力和油膜力对系统动力学进行了分析。文献[9-10]采用Muszynska密封力模型和短轴承油膜力模型对单圆盘Jeffcott转子系统的动力学行为开展了研究。文献[11]建立了双圆盘转子系统，探讨了圆盘位置尺寸、汽封压降等对系统振动特性的影响。

转子系统是一个具有复杂结构的非线性系统，线性振动理论不能很好地或全面地解决转子系统的动力学问题，实际转子系统发生故障时大多为两种或多种因素的耦合作用下同时发生且相互影响。基于此，本文基于非线性动力学和转子动力学理论，对一具有双叶轮-轴承交错布置的复杂转子系统进行研究，综合考虑非线性汽封力、油膜力和转子不平衡量的耦合作用，采用有限元法推导系统运动微分方程，建立了复杂转子-轴承-汽封系统动力学模型，并分析了系统转速、圆盘偏心量、汽封长度和汽封间隙对系统动力特性的影响。

1复杂转子-轴承-汽封系统模型

本文分析的转子-轴承-汽封系统由一根转轴、两个叶轮和两个滑动轴承组成(图1)，叶轮与轴承交错布置将转轴分为三段，非线性汽封力和油膜力分别作用在叶轮和滑动轴承上。根据有限元理论，可以把整个系统沿轴线划分为离散的圆盘、具有分布质量及弹性的轴段和轴承座等，共计4个节点单元和3个轴段单元，系统的有限元模型如图2所示。两个叶轮作为刚性圆盘分别位于节点1和节点3处，该处节点承受圆盘质量md、不平衡质量力Qd和非线性汽封力Fs的作用。节点2和节点4作为滑动轴承承受非线性油膜力Fo的作用。

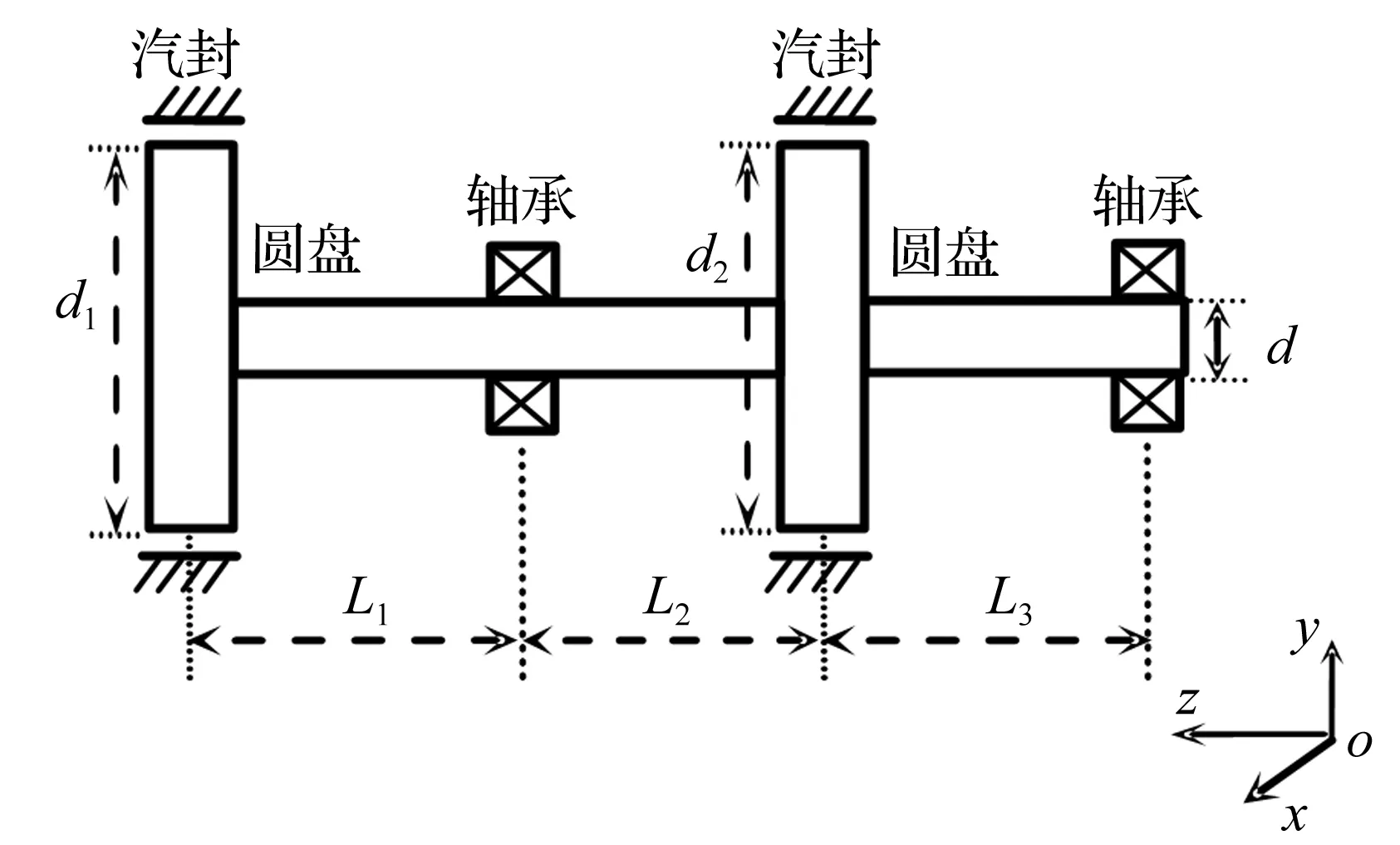
图1　复杂转子-轴承-汽封系统模型Fig.1 Rotor-bearing-seal system

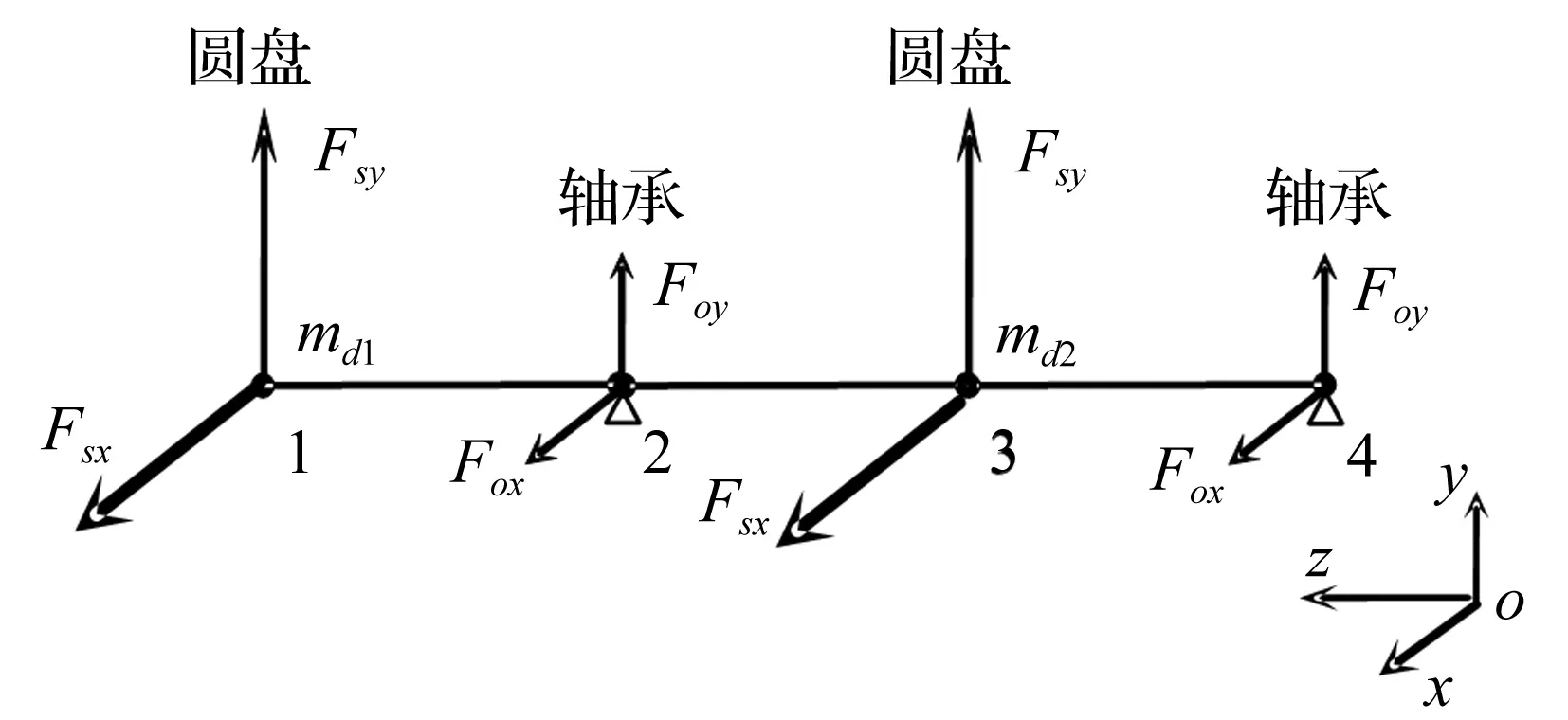
图2　转子系统有限元模型Fig.2 Finite element model of a rotor system

2部件模型

对系统的有限元模型进行单元分析建立节点力与节点位移间的关系，综合各单元的运动方程可得到广义坐标的系统运动微分方程。应用拉格朗日公式建立系统运动微分方程[12-13]：

(1)

式中，ui为广义坐标，T为动能，U为应变能，Qi为广义力。

2.1角速度与旋转坐标

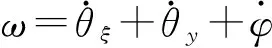
(2)

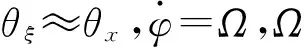
(3)

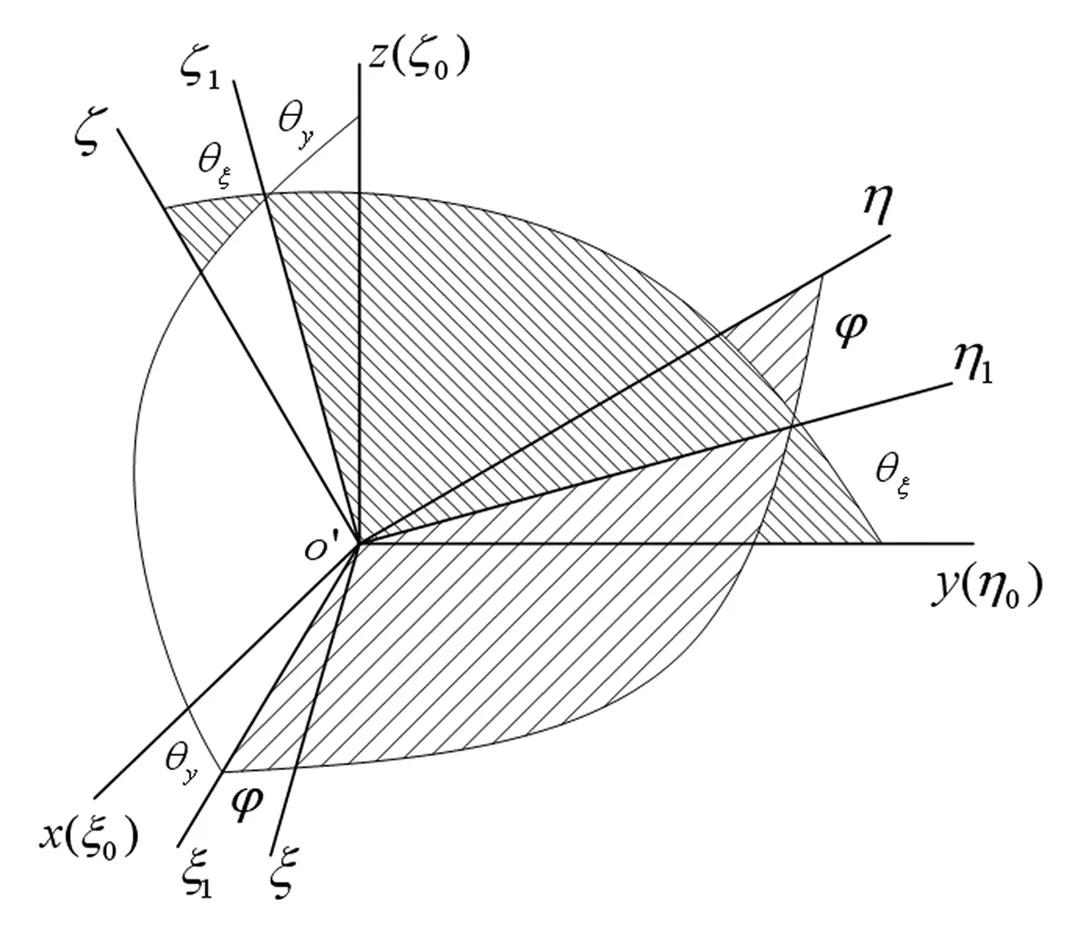
图3　坐标转换示意图Fig.3 Transformation of coordinates

2.2刚性圆盘

叶轮假设成刚性圆盘为具有4个自由度的节点，其广义坐标位移向量的表达式为{u1d}=[x,θy]T和{u2d}=[y, -θx]T。忽略应变能，其侧向弯曲振动的动能表达式：

(4)

应用式(1)，即可得出圆盘的运动微分方程为：

(5)

式中，[Md]为圆盘的质量矩阵，[Gd]=Ω[Jd]为回转矩阵，{Q1d}和{Q2d}为相应的广义力。

2.3弹性轴段

弹性轴段单元如图4所示，该单元有两个节点共8个自由度，其广义坐标为两端节点的位移向量，即

{u1s}=[xA,θyA,xB,θyB]T

{u2s}=[yA,-θxA,yB,-θxB]T

(6)

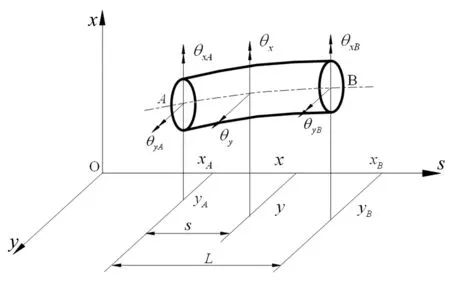
图4　弹性轴段单元Fig.4 Elastic shaft element

单元内任一截面的位移是该截面位置和时间的函数，通过位移插值函数可得：

(7)

式中，N=[N1N2N3N4]，N′=[N1′N2′N3′N4′]，

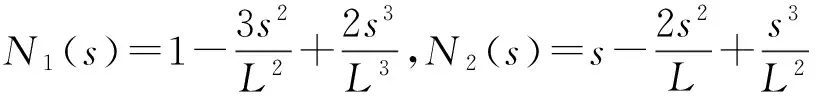
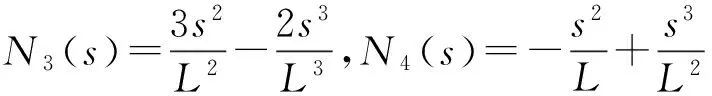
因此弹性轴段单元的动能和弯曲应变能可表示为节点位移及节点速度的函数，该单元的动能和应变能为：

(8a)

(8b)

式中，[MsT]，[MsR]为单元移动惯性矩阵和转动惯性矩阵，[Gs]=Ω[Js]为单元回转矩阵，[Ks]为单元刚度矩阵。

将式(8)代入式(1)，可得到轴段单元的运动方程：

(9)

式中，[Ms]=[MsT]+[MsR]，是考虑了移动惯性及转动惯性在内的一致质量矩阵。{Q1s}和{Q2s}为相应的广义力向量，包括节点处连接的圆盘或相邻轴段的作用力和力矩，还包括支撑的约束力和不平衡广义力。

2.4不平衡力

考虑圆盘因具有微小偏心距引起的不平衡力，如图5。不计微小偏心对Jd和JP的影响，圆盘的运动方程式(5)中的广义力包括不平衡力：

(10)

式中，e,φ分别为圆盘偏心距和偏位角。

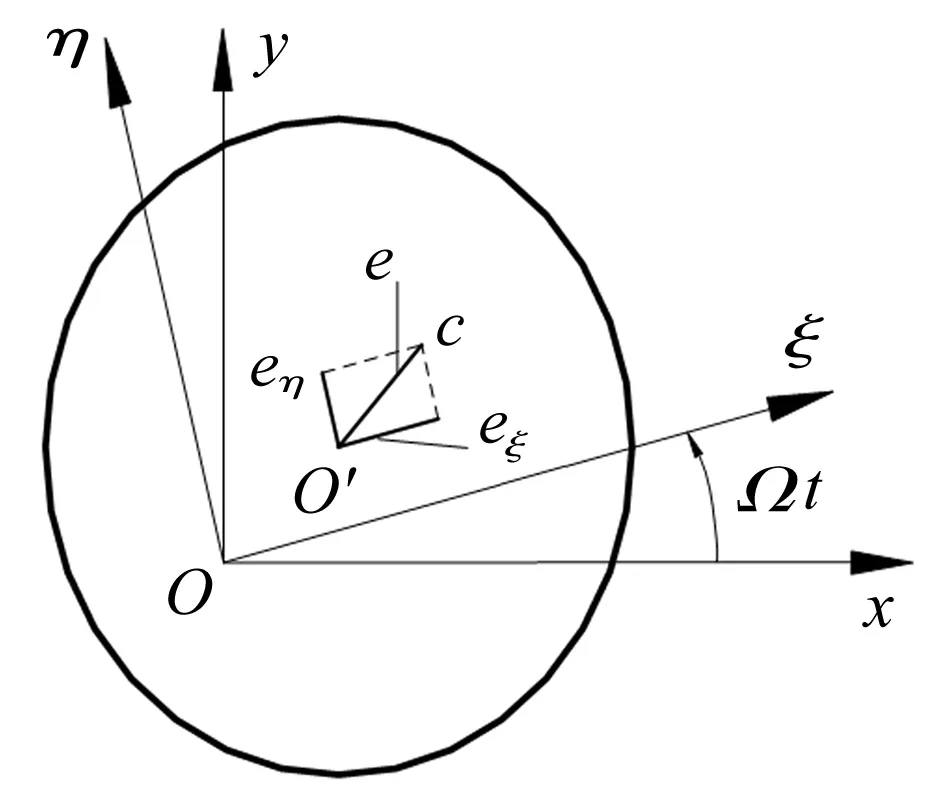
图5　偏心距引起的不平衡力Fig.5 Unbalance forces

2.5非线性汽封力

汽封流体激振力是由于汽封腔中气流有旋转，使转子和汽封腔之间的间隙变化，周向压力分布变化引起的。非线性汽封力采用Muszynska模型[14]，以流体周向平均流速比τ来表征汽封中流体的整体运动，认为流体对转子的整体作用以平均角速度τΩ旋转：

(11)

2.6非线性油膜力

滑动轴承的油膜力具有强烈的非线性特性，应用动态π油膜条件下的非稳态油膜力模型，得出短轴承非线性油膜力[15]为：

(12)

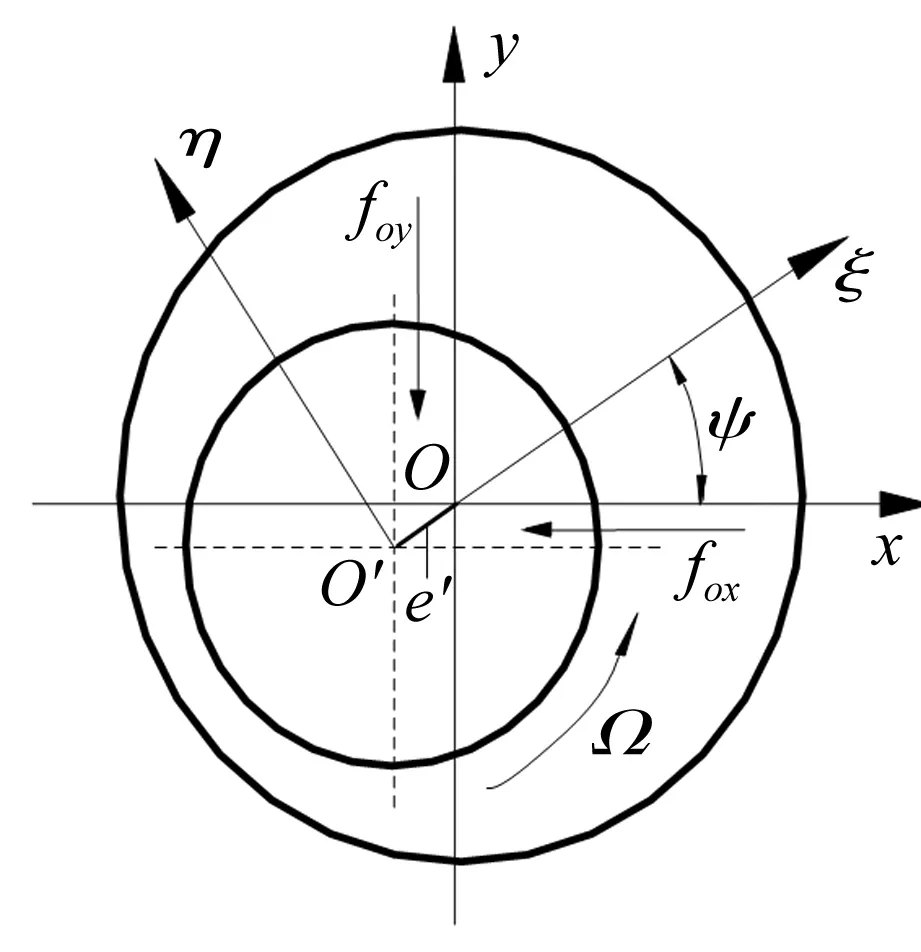
图6　轴承油膜力示意图Fig.6 Diagram of oil film forces

3系统运动方程

对于有n个节点的转子-轴承-汽封系统，将所有圆盘和轴段单元矩阵进行组装，合并单元的运动微分方程式(5)和式(9)，忽略微小的转动位移，可得转子-轴承-汽封系统有限元运动微分方程：

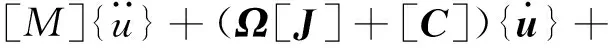
[K]{u}={Q}+{G}

(13)

式中，[M]、[J]、[C]和[K]分别为系统的质量矩阵、陀螺矩阵、阻尼矩阵和刚度矩阵，{Q}为系统的广义力，{G}为系统重力向量。

为便于计算求解，对系统运动微分方程进行无量纲化，可将上式转化为：

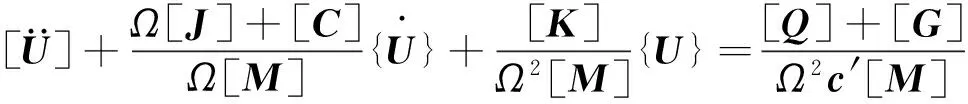
4数值计算与动力学分析

转子-轴承-汽封系统因包含汽封力和油膜力而具有高度非线性，应用数值计算方法，通过Matlab编程并使用4～5阶Runge-Kutta法对系统运动微分方程式(14)进行数值求解。采用分岔图、频谱图、相轨迹图和Poincare映射图等方法分析系统在不同参数下的非线性动力学特性。系统模型主要参数为：轴段L1=L2=250 mm，L3=500 mm；转轴直径d=50 mm；圆盘质量M1=M2=125.58 kg；圆盘直径D1=D2=500 mm；圆盘偏心距rd=0.06 mm;汽封长度Ls=50 mm，汽封间隙cs=1 mm，汽封压降ΔP=0.5 MPa；轴承长度Lb=25 mm，轴承间隙cb=0.2 mm。

4.1旋转速度的影响

对于转子-轴承-汽封系统，转子的转速是影响系统动态响应和振动特性的最重要因素之一。运用数值计算分析系统转速Ω从100 rad/s增加至1 000 rad/s区间内，圆盘(X1)和轴承(X2)的无量纲位移分岔特性(如图7)。随转速Ω的上升，系统运动规律为：周期运动→2倍周期运动→混沌运动→2倍周期运动→准周期运动→7倍周期运动→准周期运动直至混沌。当转速Ω≤370 rad/s时，系统作周期运动即系统的运动方程有且只有一个确定解，系统处于稳定运动状态。转速Ω>370 rad/s后，系统出现2倍周期分岔，表明系统由于流体诱发失稳而产生次同步振动。当转速Ω=592 rad/s时，系统运动特性由2倍周期运动变为极不稳定的混沌运动。直到转速Ω>664 rad/s时，系统再次进入2倍周期运动。当转速Ω>748 rad/s时，系统开始作准周期运动并在转速Ω在808～844 rad/s间处于短暂的7倍周期运动后，系统将随着转速的继续升高由准周期运动分岔道路最终进入混沌运动状态。

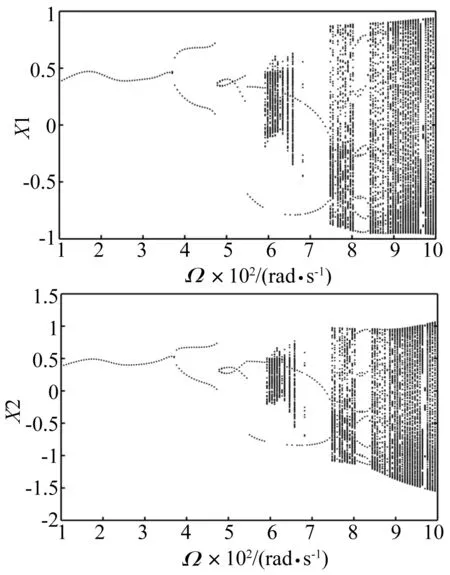
图7　系统圆盘(X1)和轴承(X2)处无量纲位移分岔图Fig.7 Bifurcation diagrams of disk(X1) and bearing(X2)

图8表征了转速Ω=200 rad/s时系统的运动特性。在此转速下，系统在频谱图上只有1倍频的单峰，相轨迹为单极限环，Poincare映射也为一孤立相点，表明系统为同步周期运动，其涡动频率与转动频率相等，系统运动稳定。图9为转速Ω=400 rad/s时系统的运动特性。此时系统不再作同步运动，相轨迹为两个连结的闭环，频谱中在1/2倍频、1倍频、3/2倍频和2倍频处有离散谱峰，Poincare映射为两个孤立相点，表明系统发生了2倍周期分岔。当转速Ω升高到610 rad/s时(图10)，系统的相轨迹以螺旋的形式发生缠绕形成奇怪吸引子，系统的频谱中存在连续谱，Poincare映射为沿曲线分布的点集并具有分形几何结构，表明系统响应处于混沌状态。图11描绘了转速Ω=810 rad/s时系统7倍周期的分频振动运动特性，此时系统频谱图上具有较明显的7个峰值，Poincare映射为7个孤立相点。系统转速Ω=950 rad/s时(图12)，频谱图显示系统除了整数倍频外还有互相不可公约的谐波分频，相轨迹为不规则形状，Poincare映射图为一条闭轨迹环，表明系统作典型的准周期运动。通过分析表明，转子-轴承-汽封系统的稳定性随系统转速的升高而降低，转速越高系统越不稳定的可能性越大。

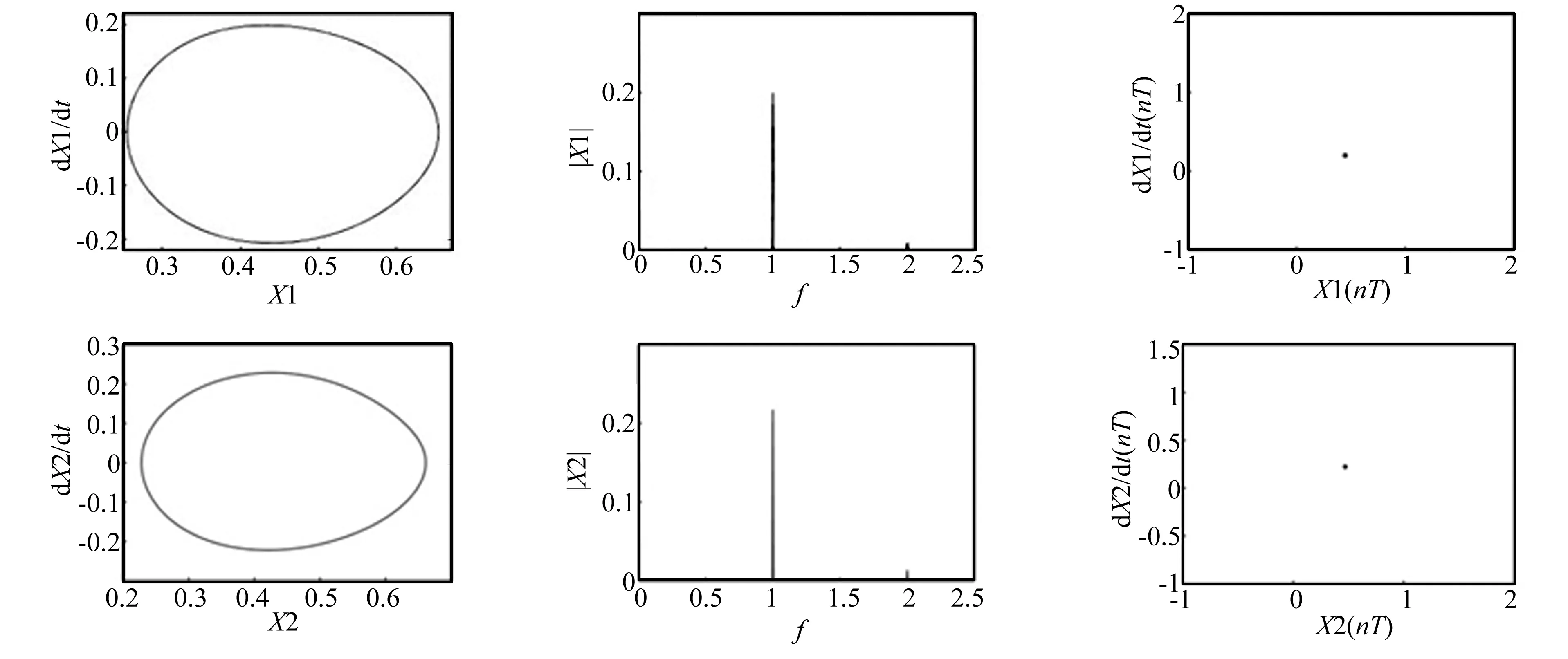
图8　转速Ω=200 rad/s时系统圆盘(X1)和轴承(X2)的运动特性图(相轨迹、频谱图和Poincare映射)Fig.8 Dynamic behavior of disk(X1) and bearing(X2) at Ω=200 rad/s

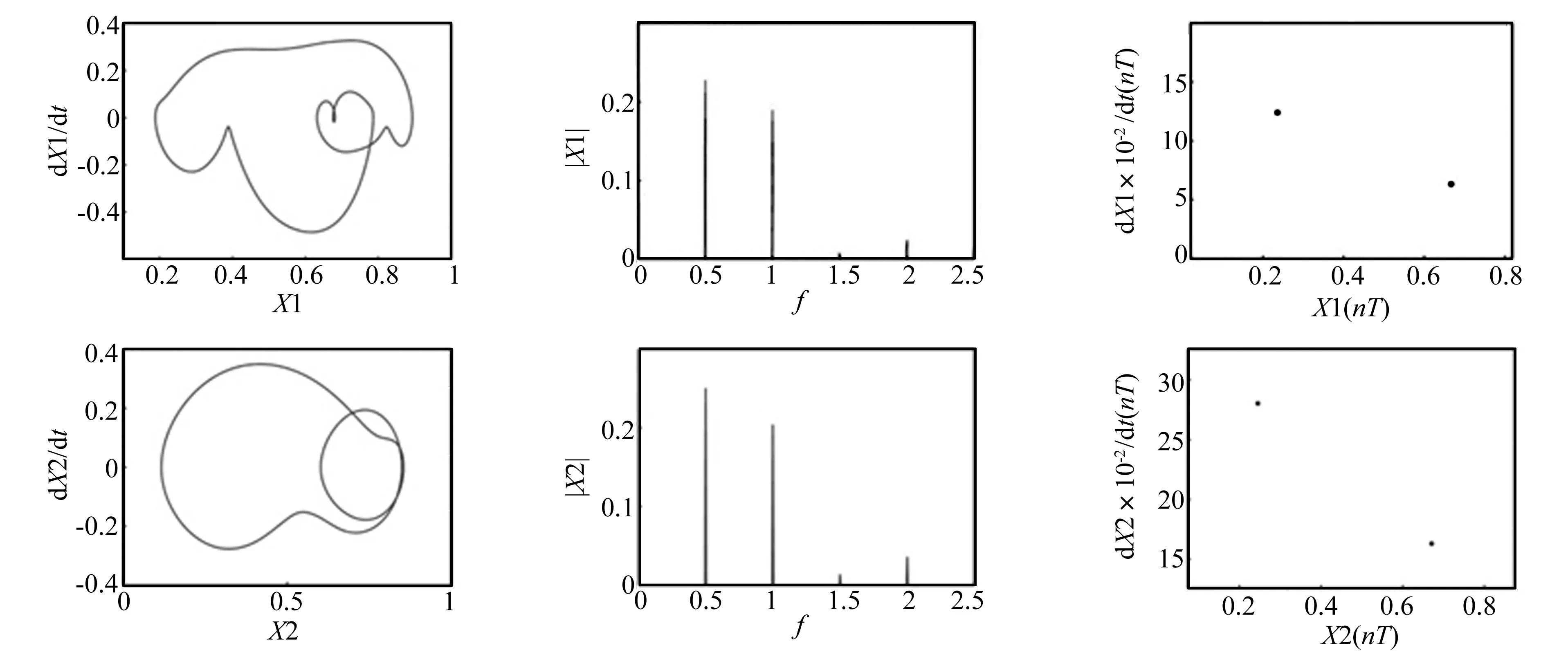
图9　转速Ω=400 rad/s时系统圆盘(X1)和轴承(X2)的运动特性图(相轨迹、频谱图和Poincare映射)Fig.9 Dynamic behavior of disk(X1) and bearing(X2) at Ω=400 rad/s

4.2圆盘偏心的影响

以1#圆盘偏心距为变量的系统位移分岔图(图13)，在汽封长度Ls=50 mm，汽封间隙cs=1 mm，汽封压降ΔP=0.5 MPa，转速Ω=500 rad/s条件下，使圆盘偏心距rd从0.001 mm增加至0.1 mm，系统运动规律为：周期运动→2倍周期运动→准周期运动→2倍周期运动→4倍周期运动→准周期运动。当偏心距rd小于0.057 mm时，系统为稳定的周期运动，随着偏心距的增大，系统出现2倍分岔并经过短暂的准周期运动，振幅迅速增大，最后进入多倍周期运动、准周期运动直至混沌呈现不稳定的运动状态。分析表明在此系统参数下，减小圆盘偏心引起的不平衡能提高转子-轴承-汽封系统运动状态的稳定性。

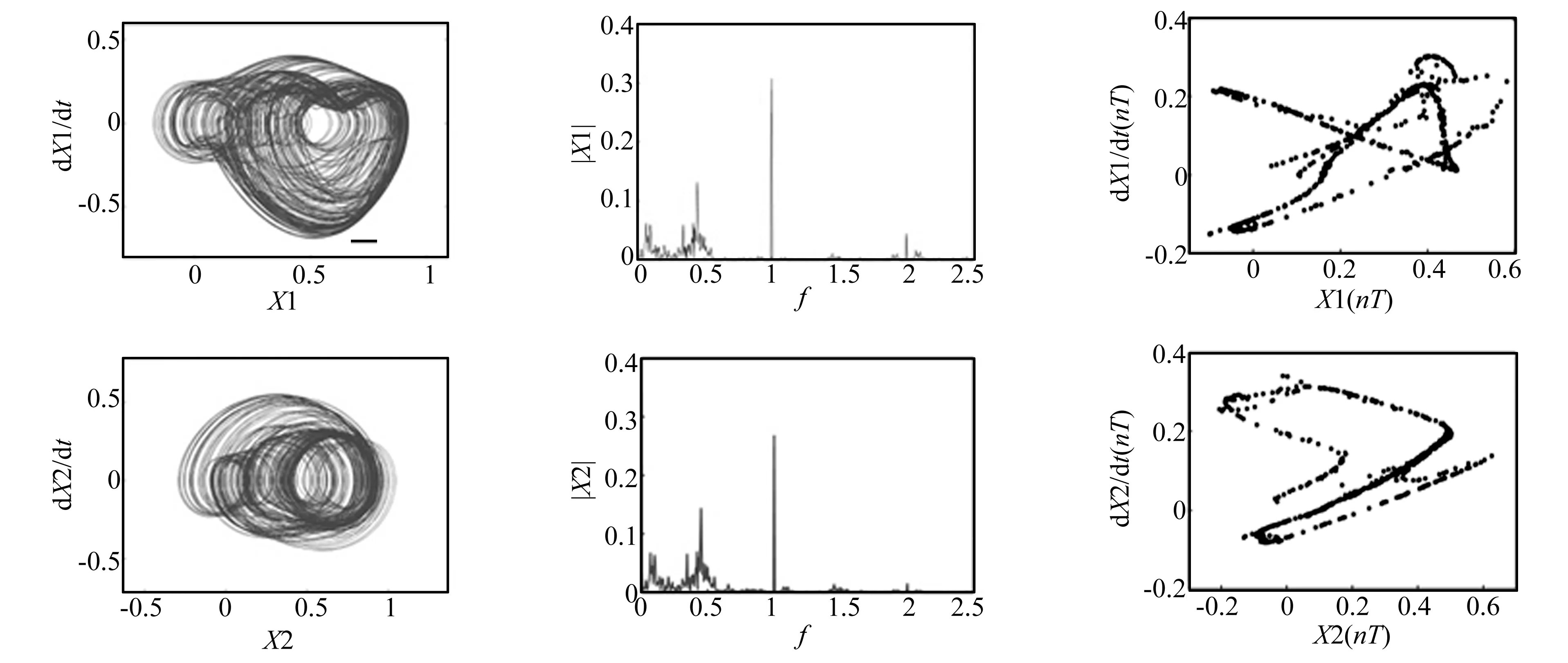
图10　转速Ω=610 rad/s时系统圆盘(X1)和轴承(X2)的运动特性图(相轨迹、频谱图和Poincare映射)Fig.10 Dynamic behavior of disk(X1) and bearing(X2) at Ω=610 rad/s

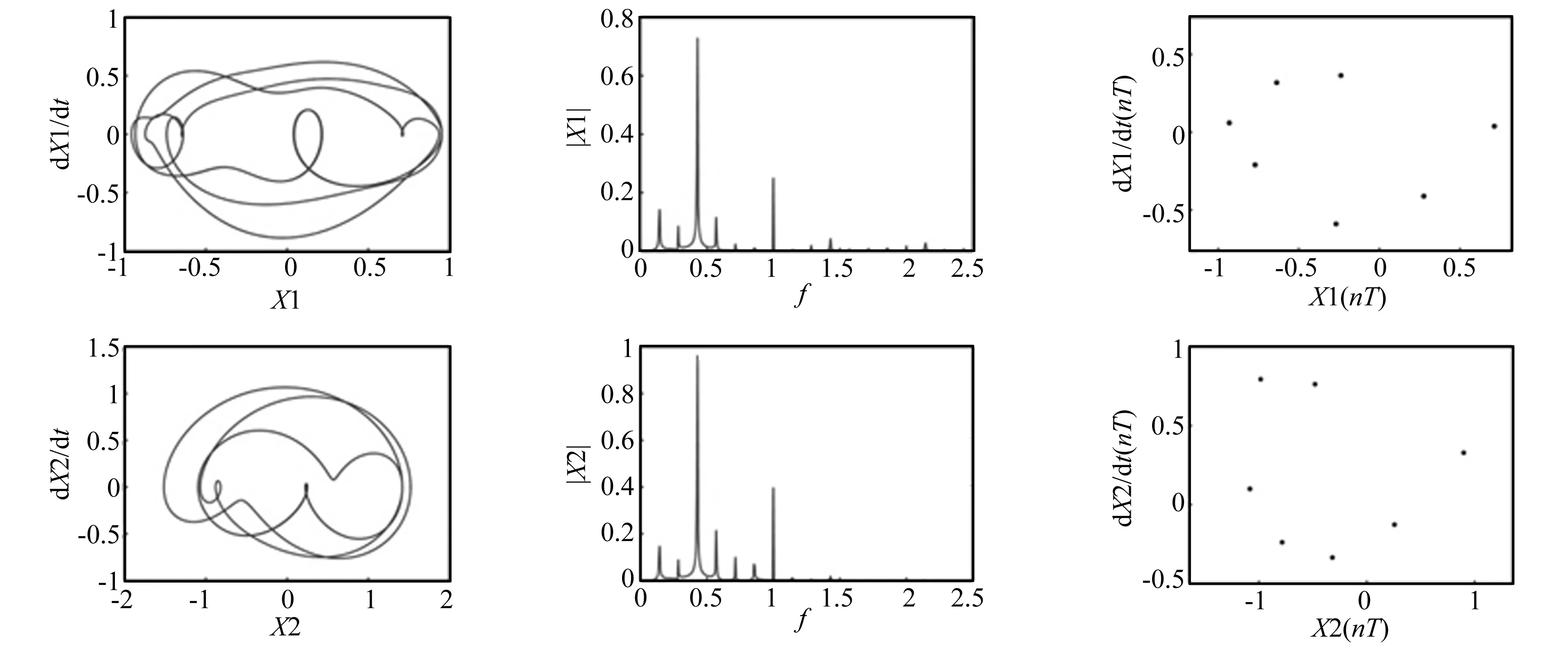
图11　转速Ω=810 rad/s时系统圆盘(X1)和轴承(X2)的运动特性图(相轨迹、频谱图和Poincare映射)Fig.11 Dynamic behavior of disk(X1) and bearing(X2) at Ω=810 rad/s

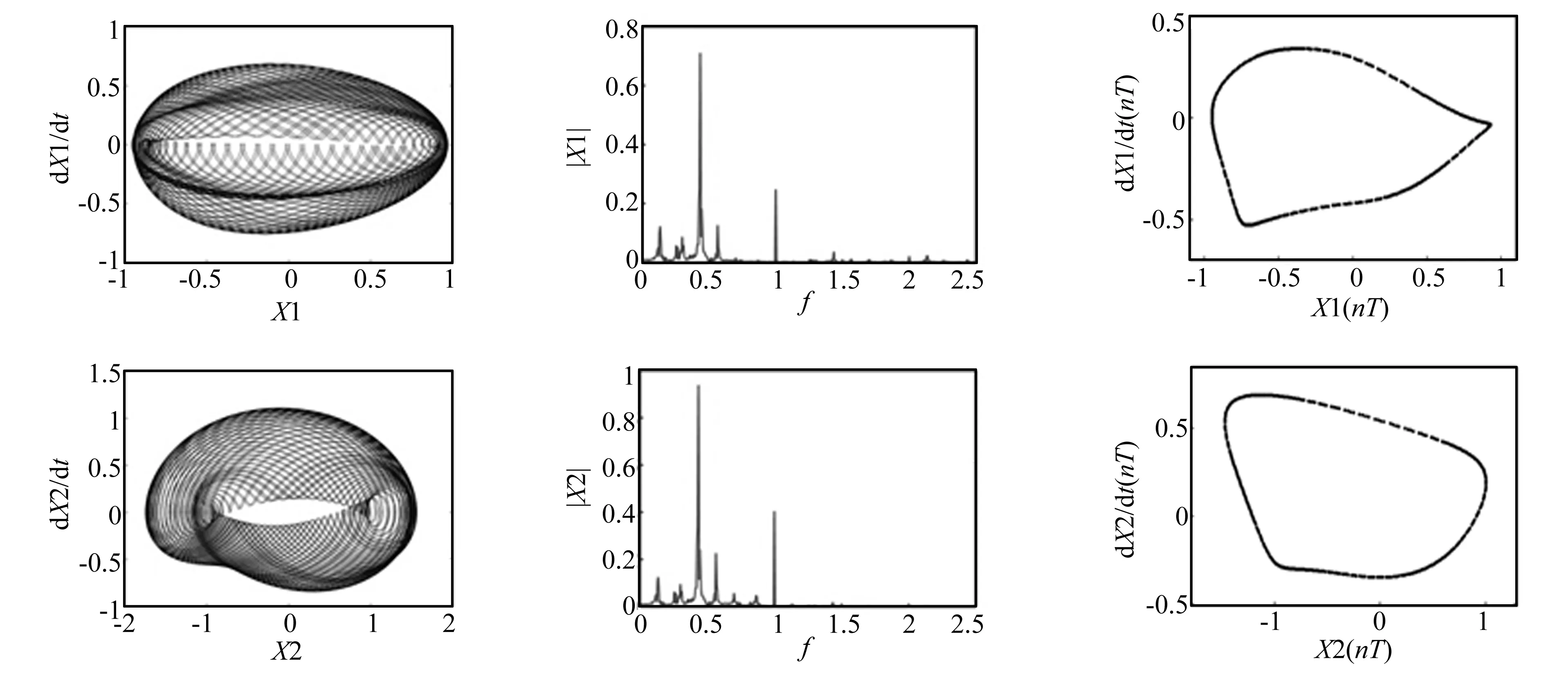
图12　转速Ω=950 rad/s时系统圆盘(X1)和轴承(X2)的运动特性图(相轨迹、频谱图和Poincare映射)Fig.12 Dynamic behavior of disk(X1) and bearing(X2) at Ω=950 rad/s

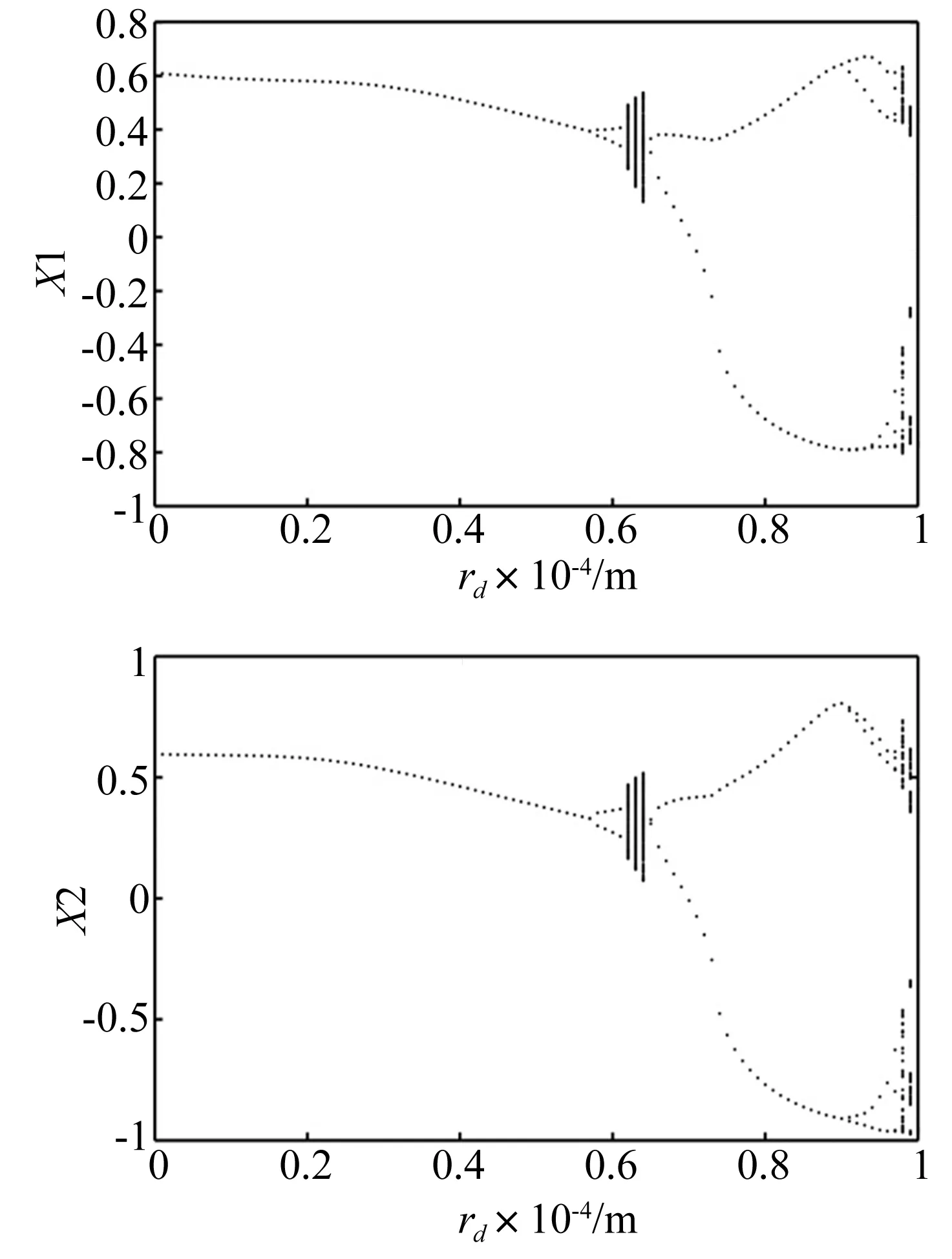
图13　系统圆盘(X1)和轴承(X2)处随偏心距变化的无量纲位移分岔图Fig.13 Bifurcation diagrams of disk(X1) and bearing(X2) with increasingrd

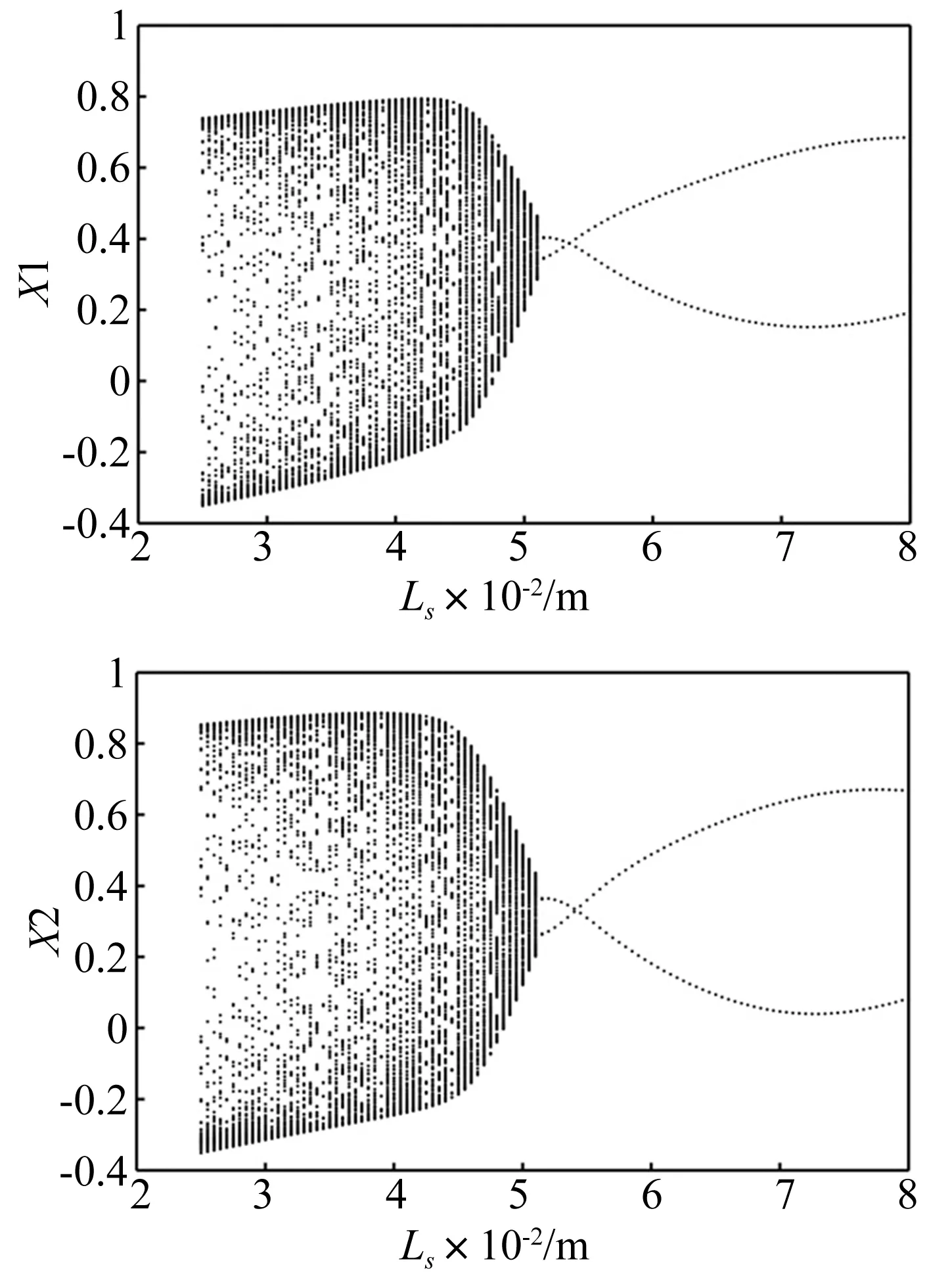
图14　系统圆盘(X1)和轴承(X2)处随汽封长度变化的无量纲位移分岔图Fig.14 Bifurcation diagrams of disk(X1) and bearing(X2) with increasing LS

4.3汽封长度的影响

图14为圆盘偏心距rd=0.06 mm，汽封间隙cs=1 mm，汽封压降ΔP=0.5 MPa，转速Ω=500 rad/s条件下，1#圆盘的汽封长度Ls从25 mm增长至80 mm间的系统位移分岔图，其运动规律为：多倍周期运动与准周期运动交替→2倍周期运动。在此参数条件下，系统振幅随着汽封长度逐渐增大而减小，当汽封长度Ls大于51 mm时，系统由准周期运动锁相进入2倍周期运动，且此周期解在其后的参数区间内稳定存在。由此系统模型参数条件得出，增加系统汽封长度有利于改善转子-轴承-汽封系统的运动特性。

4.4汽封间隙的影响

图15为圆盘偏心距rd=0.06 mm，汽封长度Ls=50 mm，汽封间隙cs=1 mm，汽封压降ΔP=0.5 MPa，转速Ω=500 rad/s条件下，汽封间隙cs在0.1～2 mm区间内变化的位移分岔图。系统运动规律随汽封间隙cs的增加呈现：2倍周期运动→周期运动→2倍周期运动。当cs小于0.22 mm或大于0.36 mm时，系统为具有较大振幅的2倍周期分岔运动。由分岔图表明，在此系统参数下，过大或过小的汽封间隙都会导致系统发生分岔而产生涡动，且过小的汽封间隙会导致轴与壳体动静碰摩，合适的汽封间隙能保证系统的稳定运行。

5结论

本文基于有限单元法和拉格朗日方程建立双叶轮-轴承交错布置的复杂转子-轴承-汽封系统的动力学模型，运用数值计算分析系统的运动特性，结论如下：

(1) 转子系统在非线性汽封力、非线性油膜力和质量不平衡等多种因素的综合作用下具有丰富的动力学行为，其运动状态随参数的变化可能呈现出周期运动、倍周期运动、准周期运动和混沌运动。

(2) 分析系统在不同转速下的相轨迹、频谱图和Poincare映射图表明，系统的稳定性随转速的升高而降低，转速越高系统运动状态越复杂。

(3)除转速外，圆盘偏心距、汽封长度和汽封间隙等参数均为系统动力学特性的重要影响因素。本文系统模型参数条件下，减小圆盘偏心，增加系统汽封长度，选取合适的汽封间隙有利于改善转子-轴承-汽封系统的运动特性。

参 考 文 献

[1] Shi Ming-lin,Wang De-zhong, Zhang Ji-ge.Nonlinear dynamic analysis of a vertical rotor-bearing system[J]. Journal of Mechanical Science and Technology,2013,27(1):9-19.

[2] 张华彪,陈予恕.非线性转子的反向全周碰摩响应[J]. 振动与冲击,2013,32(10):84-90.

ZHANG Hua-biao,CHEN Yu-shu. Reverse full annular rub of a nonlinear rotor system[J].Journal of Vibration and Shock,2013,32(10):84-90.

[3] Wu J J. Prediction of lateral vibration characteristics of a full-size rotor-bearing system by using those of its scale models[J]. Finite Elements in Analysis and Design,2007,43:803-816.

[4] 何洪军,荆建平. 非线性转子-密封系统动力学模型研究[J]. 振动与冲击,2014,33(10):73-76.

HE Hong-jun,JING Jian-ping. Dynamic model of a nonlinear rotor-seal system[J]. Journal of Vibration and Shock,2014,33(10):73-76.

[5] Zeng Yun, Zhang Li-xiang,Guo Ya-kun,et al.The generalized Hamiltonian model for the shafting transient analysis of the hydro turbine generating sets[J]. Nonlinear Dynamics,2014,76(4):1921-1933.

[6] Muszynska A. Improvements in lightly loaded rotor/bearing and rotor/seal models[J]. Journal of Vibration,Acoustics,Stress,and Reliability in Design,1988,110(2):129-136.

[7] Muszynska A,Bently D E. Frequency-swept rotating input perturbation techniques and identification of the fluid force models in rotor/bearing/seal systems and fluid handling machines[J]. Journal of Sound and Vibration,1990,143(1):103-124.

[8] Li Wei,Yang Yi,Sheng De-ren,et al. Nonlinear dynamic analysis of a rotor/bearing/seal system[J]. Journal of Zhejiang University-SCIENCE A:Applied Physics & Engineering,2011,12(1):46-55.

[9] 成玫,孟光,荆建平.转子-轴承-密封系统的非线性振动特性[J].上海交通大学学报,2007,41(3):398-404.

CHENG Mei,MENG Guang,JING Jian-ping.The nonlinear dynamical behaviors of a rotor-bearing-seal system[J]. Journal of Shanghaijiaotong University,2007,41(3):398-404.

[10] 成玫,孟光,荆建平.非线性“转子-轴承-密封”系统动力分析[J]. 振动工程学报,2006,19(4):519-524.

CHENG Mei,MENG Guang,JING Jian-ping.Dynamic analysis of a rotor-bearing-seal nonlinear system[J]. Journal of Vibration Engineering,2006,19(4):519-524.

[11] Zhou Wen-jie,Wei Xue-song,Wei Xian-zhu,et al.Numerical analysis of a nonlinear double disc rotor-seal system[J]. Journal of Zhejiang University-SCIENCE A:Applied Physics & Engineering,2014,15(1):39-52.

[12] 于海,陈予恕,曹庆杰.多自由度裂纹转子系统非线性动力学特性分析[J]. 振动与冲击,2014,33(7):92-98.

YU Hai,CHEN Yu-shu,CAO Qing-jie. Nonlinear dynamic behavior analysis for a cracked multi-DOF rotor system[J]. Journal of Vibration and Shock,2014,33(7):92-98.

[13] Li Wei,Yang Yi,Sheng De-ren,et al. A novel nonlinear model of rotor/bearing/seal system and numerical analysis[J]. Mechanism and Machine Theory,2011,46:618-631.

[14] 李忠刚,孔达,焦映厚,等. 转子-密封系统非线性动力学特性分析[J]. 振动与冲击,2009,28(6):159-163.

LI Zhong-gang,KONG Da,JIAO Ying-hou,et al. Nonlinear dynamic analysis of a rotor-seal system[J]. Journal of Vibration and Shock,2009,28(6):159-163.

[15] 徐小峰,张文.一种非稳态油膜力模型下刚性转子的分岔和混沌特性[J].振动工程学报,2000,13(6):247-252.

XU Xiao-feng,ZHANG Wen. Bifurcation and chaos of rigid unbalance rotor in short bearings under an unsteady oil-film force model[J]. Journal of Vibration Engineering,2000,13(6):247-252.

Vibration analysis of a nonlinear rotor-bearing-seal system

YUAN Ming-hong1, TONG Shui-guang1,2, CONG Fei-yun2, LI Fa-zong1

(1. Institute of Thermal Engineering and Power Systems, Zhejiang University, Hangzhou 310027, China;2. Institute of Mechanical Design, Zhejiang University, Hangzhou 310027, China)

Abstract:Based on the theory of nonlinear dynamics and rotor dynamics, a new complicated rotor-bearing-seal system dynamic model with double-impeller-bearing staggered arrangement considering Muszynska’s nonlinear seal force, the nonlinear oil film force and the mass eccentricity of the disk was proposed. The finite element method(FEM) was applied to derive the motion differential equations of the system and analyze the effects of system speed, disk eccentricity, seal length and seal clearance on the dynamic characteristics of the system. By using bifurcation diagrams, frequency spectra, phase trajectory maps, and Poincare maps, the dynamic state of the system was presented. The studies demonstrated that the coupled system is highly nonlinear; with parameters’ change, the system reveals rich forms of its dynamic behaviors including periodic, multi-periodic, quasi-periodic and chaotic motions; small disk eccentricity, long seal length and suitable seal clearance is helpful to improve the stability of the system.

Key words:nonlinear vibration; rotor-dynamics; finite element method (FEM); bifurcation; chaos

基金项目：国家自然科学基金资助项目(51305392)；浙江省重大科技专项(2013C01150)

收稿日期：2015-03-16修改稿收到日期：2015-05-14

通信作者童水光 男，教授，博士生导师，1960年生

中图分类号:O322；TH133

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.011

第一作者 袁铭鸿 男，博士生，1987年11月生