“可能性”的教材分析与教学实践

◇胡重光 许建刚

“可能性”的教材分析与教学实践

◇胡重光 许建刚

一 研究概率知识的意义

概率论与数理统计在数学中具有特殊的地位。

自然界和人类社会中的各种现象可以分为两类。一类是结果可以预先确定的现象。例如，抛到空中的重物总是落回地面；在一个标准大气压之下，水总在100℃沸腾；水稻的生长总是经历发芽、长叶、分蘖、吐穗、扬花、结实这几个阶段；等等。这类现象称为确定性现象或必然现象。几何、代数、数学分析、微分方程等数学分支就是研究这类现象的工具。另一类是结果不能预先确定的现象。例如，抛一枚质地均匀的硬币，落下后可能正面朝上，也可能反面朝上；新生儿可能是男婴，也可能是女婴；下周一可能下雨，也可能不下雨；等等。这类现象称为偶然现象或随机现象。

人们通过长期的观察和实践逐渐发现，在相同的条件下，大量出现的偶然现象也存在规律。例如，多次抛一枚质地均匀的硬币，落下后正面朝上和反面朝上出现的次数之比总是接近1∶1，并且抛的次数越多，越接近这个比；即使是偶然性很强的天气变化，也存在一定的规律，经过长期的研究和实践，天气预报的准确性已越来越高；等等。正如恩格斯所指出的：“表面上看起来是偶然性在起作用的地方，其实这种偶然性始终是受内部隐藏着的规律支配的，而问题只是在于发现这些规律。”大量的随机现象所呈现的这种规律，称为随机现象的统计规律。数理统计就是研究随机现象的统计规律的科学，概率论则是数理统计的数学基础。

现实中存在大量的随机现象，研究这些随机现象的统计规律是人类的重要任务。当代社会信息量激增，科学研究和生产实践经常需要收集和处理大量的数据，因此概率论与数理统计广泛地应用于从自然科学到社会科学的各门学科中，工商企业及政府的决策都离不开概率论与数理统计。

二 “可能性”的教材分析

概率基础知识在发达国家的小学数学教学中受到高度重视。我国的小学数学教学引入概率知识较晚，直到2001年开始的基础教育课程改革才引入。教材中没有出现“概率”这一名称，而是称为“可能性”。

概率启蒙知识的教学要使学生明白：现实中存在必然现象，也存在偶然现象；大量的偶然现象中存在规律。这样学生就能感受到学习这一知识的必要性。这是“可能性”教学的首要目标。

2013年出版的人教版教材在五年级上册编排“可能性”的知识。该单元安排了大量活动，有抽节目、观察棋子或摸棋子、转指针、抛硬币、掷骰子。有的活动要求通过摸棋子来判断哪种颜色的棋子多；有的活动让学生列表统计，将概率与统计结合起来。这些都是很有益的活动。但这些活动都是人为的，都不涉及自然现象，并且应用性不强。这样就难以达到上述教学目标。

要达到上述教学目标，应该举出现实中普遍存在的随机事件作为例子。《义务教育数学课程标准（2011年版）》要求让学生“在具体情境中，通过实例感受简单的随机现象”，就是这个意思。

“事件”是概率论的一个最基本的概念。概率论的教科书对事件有明确的定义：随机试验的结果叫随机事件，简称事件（这与日常生活中“事件”一词的意义是根本不同的）。由这一定义可知：要弄清事件的概念，首先要明确试验和随机试验的概念。“试验”是一个常用词，通常认为：为了解某物的性能或某事的结果而进行的尝试性活动叫试验。但是在概率中，观察在一定条件下发生的现象（包括自然现象）也叫试验。例如，观察天气变化就是试验。那么什么是随机试验呢？它要满足以下三个条件。

（1）在相同的条件下试验可以重复进行或结果重复出现；

（2）每次试验可能出现的结果不止一个，但是能事先确定每次试验所有可能出现的结果；

（3）试验之前不能确定会出现哪一个结果。

仔细揣摩概念的含义，可以发现，列举事件的例子时，要注意以下几点。

（1）区分事件与现象。例如，“月亮绕着地球转”是现象，不是事件；“下月出现月全食”是这一现象可能出现的结果，所以是事件。

（2）事件具有预测性。因为在试验前不能确定会出现哪一个结果，所以事件具有预测性。例如，在当前，“希拉里当选美国总统”是事件，“奥巴马当选美国总统”则不是事件。“我从出生到现在没有吃过一点东西”是已经过去的事，所以不是事件。

（3）事件具有动态性。事件是一次试验或某种现象的结果，所以必然涉及某种活动，因而具有动态性。例如，“三天后下雨”就涉及“天气”这一自然现象，天气是不断变化的，具有动态性。而“花是香的”并不涉及某一试验或现象，它只是一个判断。“判断”只有对错之分，而没有一定发生、可能发生、不可能发生之分。把判断句作为事件的现象在教学中经常出现。例如，有的试卷把“六月一日是儿童节”之类的判断句作为必然事件。

（4）正确取舍生活性和科学性。《全日制义务教育数学课程标准（实验稿）》中有一个事件的例子：下周三本地下雨。实验教材则改为“三天后下雨”。看起来似乎不够严谨，但作为日常习惯说法，如果下雨的地点就是本地，是不必指出来的。教材中还给出了“太阳从西边升起”这个例子，虽然生活中“太阳从西边升起”常常用来指不可能发生的事，从生活的角度看，作为不可能事件的例子是恰当的，但这一习惯用语是违反科学的——所谓“太阳升起”不过是地球自转造成的错觉——不像“三天后下雨”只是做了省略，特别是小学的科学课中已经介绍了太阳系，因此就不宜将其作为不可能事件的例子了。

在一定条件下，必然会发生的事件称为必然事件，如在一个标准大气压下，水加热到100℃必然会沸腾；必然不会发生的事件称为不可能事件，如在没有外力作用的条件下，做匀速直线运动的物体改变其运动状态是不可能的。需要说明的是：必然事件与不可能事件可以说不是随机事件，但为了研究的方便，我们把必然事件与不可能事件作为随机事件的两个极端情形来统一处理。

看来要正确列举合适的事件并不那么容易。其实，我们并不需要列举大量的事件，举几个学生熟悉的例子即可说明问题。第一个应该是天气，这是最常见又是学生最熟悉的偶然现象。天气变化无常，但又有规律可循。大量的天气谚语就是人们通过长期观察总结出来的规律。例如，春寒有雨，春暖得晴；春无三日晴，夏无三日雨；瓦块云，晒死人；等等。可以让学生说出他们知道的天气谚语。短期的天气可以预报，但有时也不准确。第二个是各种抽奖活动。此类活动较多，学生多半都经历过，并且很感兴趣。他们渴望中大奖，但经验告诉他们，中奖是凭运气的，谁也无法左右，中大奖的可能性总是很小的，而中小奖的可能性则比较大。为什么会这样？他们很想知道。

当然，多拥有一些例子总能使教学更加游刃有余，下面提供一些例子供参考。

（1）玩“锤子、剪刀、布”游戏时，对手出哪一种手势。

（2）下次数学考试你的得分。

（3）在海边生活时，水加热到100℃沸腾。

（4）某次摸奖活动设一、二、三等奖，有人摸到一等奖。

（5）下周一某超市的营业额。

（6）长沙市明年7月份下雪。

（7）明年你家果园的水果产量。

（8）用尺量一个物件的长度没有误差。

（9）明年本地发生地震。

（10）抛5次硬币落下后全部正面朝上。

以上现象是生活中常见的，学生大多比较熟悉，不熟悉的也很容易理解。值得注意的是：上述例子中，（3）是一个必然事件；（8）是一个不可能事件（因为量长度时用肉眼看没有误差，用放大镜看可能有误差。只要不断加大放大镜的倍数，总会发现有误差。这个例子使学生懂得，只要涉及现实问题，精确总是相对的，这对他们今后的数学学习是很有好处的）；（10）却是一个可能发生的事件，尽管发生的可能性很小。

三 “可能性”的学习活动

概率论的教科书一般都把抛硬币作为一个例子，以说明在大量重复的试验中，随机试验呈现出规律性，并介绍历史上几个著名的抛硬币试验。最有名的是蒲丰和皮尔逊的试验。皮尔逊进行了两次试验，分别抛了12000次和24000次，而且是在蒲丰进行了“抛硬币 4040次”试验之后。当然，没有记录下来的试验数不胜数。数学家们为什么非要亲自做试验呢？应该说是强烈的探索精神和严谨的科学态度促使他们这样做的。这正是进行数学研究所需要具备的素养。弗赖登塔尔主张让学生“再创造”数学，即重新发现数学家已经发现的东西。由此看来，我们也应该让学生重做这个试验。

为了在时间有限的课堂上完成这个试验，可以采取小组合作的方式进行。将全班学生分成4到8人一组，每组发一张表。首先每人抛一枚硬币10次（为操作方便，可以每人准备一个鞋盒，抛时用拇指和食指捏住硬币，停在鞋盒上方半米左右的地方，然后松手，让硬币掉进鞋盒）；其次记下正面出现多少次；最后填表。先填出抛币次数（N）和正面朝上次数（Z），再计算各自的正面朝上次数除以抛币次数所得的商（Z/N）。第一组填完整的表格如表1所示。

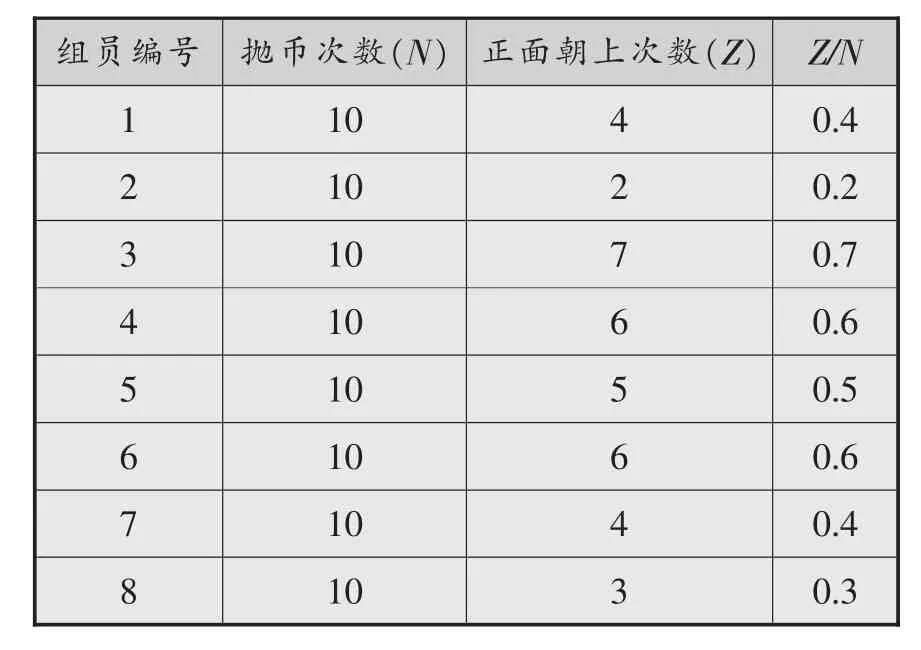
表1

完成后将表交给老师，老师再根据各组的表统计出各组的正面朝上次数（如表2）。然后各组同学分别计算本组的Z/N和全班的Z/N（可使用计算器计算，统一用“四舍五入”法保留四位小数。下同）。

表2

至此，每个学生得到了三个Z/N的数据，将这三个数据填在表3中。

表3

让各组讨论：通过上面的活动，你有什么感想？有什么发现？

通过讨论，学生不难发现：抛出的硬币落下后正面朝上还是反面朝上是随机的，无法事先确定；抛的次数越多，落下后正面朝上的次数越接近一半。这正是“可能性”教学必须达到的重要目标。

这一活动不但让学生自己抛硬币，而且让他们自己计算和统计，并进行总结性的讨论，所有结论都是学生自己得出的。也就是让学生亲历了一次数学研究活动。这类活动不需要安排很多，重要的是应尽可能让学生独立完成，让他们充分体验、充分感悟。

教师还可以用表格呈现历史上一些著名的抛硬币试验，让学生观察。（如表 4）

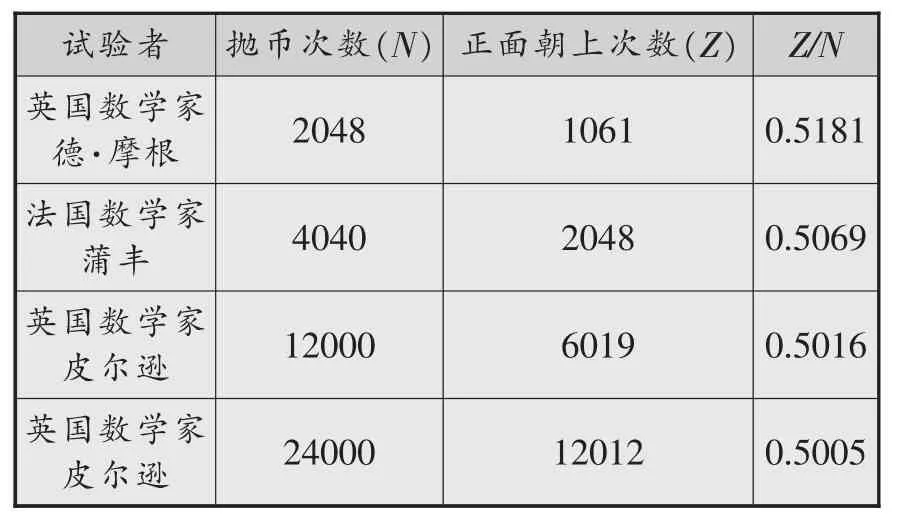
表4 ：历史上一些著名的抛硬币试验

还可以介绍美国数学家维尼的试验方法，因为他的方法与我们的有点类似。他做了10组抛硬币的试验，每组抛2000次，得到的数据及分析如表5所示。

表5 ：维尼抛硬币试验数据表

数学家们的这种执着精神令学生惊叹，更加精密的数据进一步加强了学生的信念，也使学生对数学的严谨性产生深刻的印象。这些都是数学教育的重要目标，它们比数学知识学习本身更重要。

从表中可以看到两个有意思的现象：表5中第八组的数据0.5010比总计的数据0.4989更接近0.5；表4中没有出现Z/N恰好等于0.5的试验，但是在学生自己做的试验中，却出现了Z/N恰好等于0.5的结果（出现的概率约为 0.2461，接近0.25）。这里面包含着一些深刻、有趣的道理：某组的数据比总计的数据更理想，这是总趋势中的偶然现象（前面学生的抛硬币试验中也会出现这种现象）；抛币的次数越多，正面朝上的次数越接近一半，但越不可能恰好等于一半。这些有趣的现象会激起儿童强烈的探索欲望。

[1]齐民友.概率论与数理统计[M].北京：高等教育出版社，2002.

[2]张奠宙，等.大千世界的随机现象[M].南宁：广西教育出版社，1999.

（作者单位：湖南第一师范学院，国防科技大学附属小学）

湖南省高校哲学社科重点研究基地“小学教师教育研究基地”；湖南省教育科学“十二五”规划课题“课程标准小学数学实验教材研究”】