APF中一种改进的变步长LMS自适应谐波检测算法

吕广强，刘 娱，段海军

(南京理工大学自动化学院，江苏 南京 210094)

APF中一种改进的变步长LMS自适应谐波检测算法

吕广强，刘 娱，段海军

(南京理工大学自动化学院，江苏 南京 210094)

在有源电力滤波器(Active Power Filter, APF)的低信噪比(Signal Noise Ratio, SNR)环境下，为了提高变步长最小均方(Least Mean Square, LMS)自适应算法对谐波电流检测的跟踪速度及精度，提出改进的变步长LMS算法。该算法在MVSS-LMS算法的基础上，增加历史误差的遗忘加权和估计并控制步长更新，动态控制步长更新范围，采用滑动窗遗忘加权减小了计算复杂度。同时，对改进算法性能进行稳定性分析。实验结果表明，该算法不仅具有较快的动态响应速度，而且在APF的低信噪比情况下，稳态误差有所减小，具有较高的抗干扰能力，谐波电流检测效果较好。

有源电力滤波器；谐波检测；变步长；最小均方；自适应算法

0 引言

随着电力工业的发展，大量非线性负荷的投入带来了一系列谐波和不平衡问题。有源电力滤波器(APF)是近年来发展起来的一种抑制电网谐波的有效手段[1]。有源电力滤波器能够快速地动态跟踪补偿谐波和无功功率， 其谐波检测环节的检测精确度及速度直接影响着APF的滤波性能好坏。

现有的谐波检测算法有快速傅里叶变换(Fast Fourier Transformation, FFT)[2]、瞬时无功功率理论、小波变换等[3-4]。这些检测算法各有特点，但存在着一些共性的问题：检测系统开环，并且频率固定，所以对元件参数和电网频率的变化比较敏感[5]。相较于上述算法，由于自适应滤波算法是闭环系统，能够根据电网变化自动调整滤波器的参数，改变权值系数，最终实现最佳的滤波效果，并且自适应滤波可以适用于单相及三相系统[6]，更符合APF的谐波检测要求。

文献[7]开始将定步长自适应滤波算法应用于APF的谐波检测中。但传统定步长自适应算法的步长选择无法兼顾谐波检测算法要求的收敛速度和稳态精度[8]。为此，许多学者提出变步长自适应算法。所谓变步长即步长在系统初始阶段或参数发生变化时，步长自适应增大，提高算法的收敛速度和跟踪能力，算法收敛后不管有多大扰动，算法保持较小步长以实现较小的稳态误差。

文献[9]中的变步长自适应算法使步长随迭代次数的增加而逐渐减小，但该算法对主输入端干扰信号非常敏感，步长不易收敛。文献[10]提出VSS-LMS算法，通过均方瞬时误差来调节自适应步长，但算法易受到独立噪声影响。文献[11]提出MVSS-LMS算法，应用当前误差和上一次误差的自相关函数来控制步长更新，在一定程度上消除了噪声中不相关成分的干扰。具体应用于APF时，由于信噪比较低，上述算法的跟踪波形会产生一定的稳态失调误差，而且当负载突变时，跟踪精度会随之降低。

本文提出一种改进的适用于APF的变步长LMS自适应谐波检测算法以解决传统变步长算法在APF应用时的问题。改进算法中权值调整的依据是误差信号自相关估计函数，并引入历史误差的遗忘加权和来减缓瞬时误差相关性过小造成的步长衰减过快，从而降低了APF应用时信噪比较低情况下的稳态失调，增强了算法对噪声的抗干扰性。实验结果表明该方法增快了算法的跟踪速度，提高了跟踪精度，同时减小了稳态失调误差，具有较好的自适应能力。

1 自适应谐波检测原理

1.1 自适应噪声对消法原理

自适应噪声对消技术是在信号处理中提出的一种信号处理方法，该方法具有自学习能力和自我调节能力，使检测系统在最优工作状态下，将期望信号从加性噪声中分离出来。其工作原理如图1所示。

图1 自适应噪声对消法原理图Fig. 1 Adaptive noise canceling method principle diagram

1.2 APF的自适应谐波检测算法

将自适应噪声对消法应用于APF，其结构如图2所示。

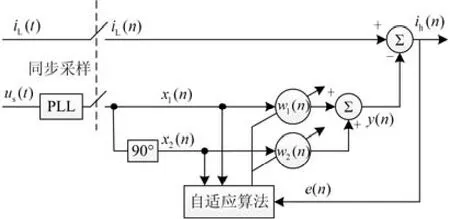
图2 自适应谐波检测算法框图Fig. 2 Principle scheme of adaptive harmonic detecting algorithm

由LMS算法，m为固定步长因子，迭代公式为

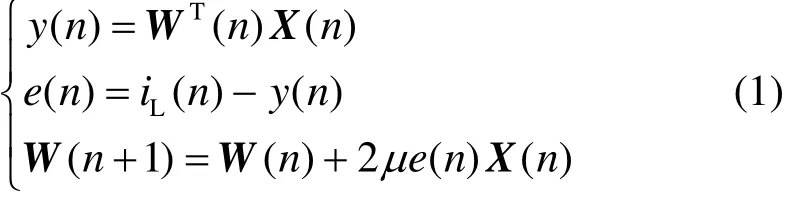
1.3 传统变步长LMS算法

传统定步长LMS算法的内在局限决定其在收敛速度和稳态失调之间的要求无法兼顾[8]。变步长LMS算法可以较好地解决此矛盾，其实现方法为：当权值系数远离最佳权值，步长相应增大，从而获得较快的动态响应速度和更强的跟踪能力；当权值系数接近最佳权值步长自适应减小并保持在较小数值，以获得较小的稳态误差。

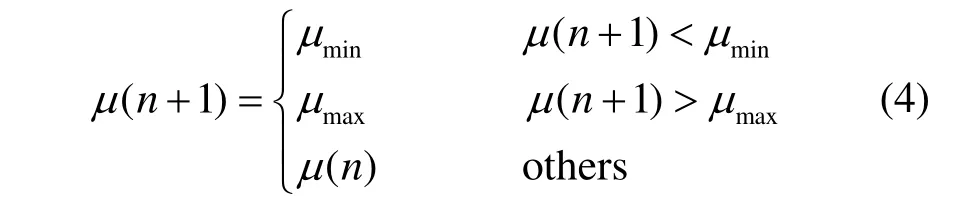
式中，minm和maxm的取值参考文献[12]。

MVSS-LMS算法在一定程度上消除了噪声中不相关成分的干扰，但由于在收敛过程中，关性较小，导致算法经常在未收敛前，步长就减小到最小值[13]，造成算法动态响应速度较慢，跟踪效果不够好。

2 改进的变步长LMS自适应算法

2.1 改进算法

针对现有变步长算法的不足，本文在MVSS-LMS 算法的基础上，引入历史误差的遗忘加权和，补偿到中来控制步长更新，改进MVSS-LMS相关性较小所导致的步长过快衰减以至动态响应速度较慢的问题，同时保留抗噪声干扰能力。本文提出的新的变步长自适应LMS算法的具体公式为

2.2 参数选择

2.3 算法复杂度分析

将式(7)整理可得

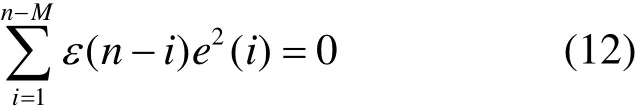
2.4 稳定性能分析

参照文献[15]所述方法对算法的稳定性能进行分析。

将式(5)改写成另一种表达式(13)。

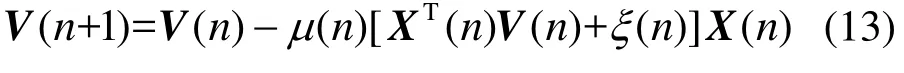
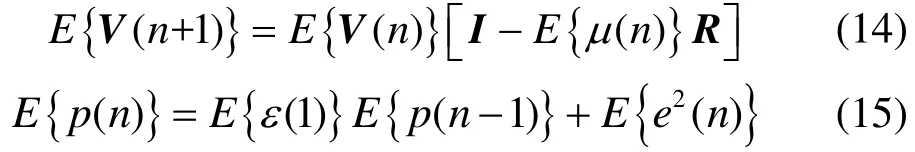
若步长、权矢量及输入信号矢量之间是统计独立的，则可如下推导出步长均值的稳定性条件。

步长迭代公式(8)展开为

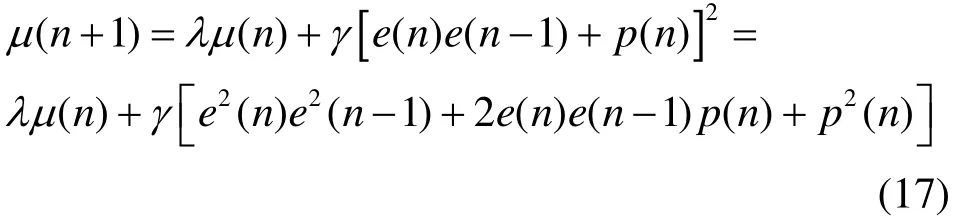
则改进算法的步长因子一阶统计特性为

记Q为

的收敛稳态值，取决于待检测信号的谐波含量。因此

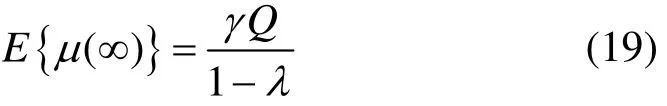
3 实验分析

为了检验本文所提出的改进变步长LMS算法性能，在TI公司的TMS320F28335浮点数字信号处理器(Digital Signal Processing, DSP)上实现该算法。同时采用交流谐波源产生单相电流信号，实验对比定步长算法、MVSS-LMS算法和改进算法的谐波检测性能。

各算法的参数设置如表1所示，主要参数的取值在保证几种算法的跟踪性能和检测精度具有参考价值的基础上保持一致。为了保证较快的响应速度，各算法的步长初值都为0.1，初始权值为零矢量。

表1 各算法的实验参数Table 1 Experimental parameters of each algorithm

实验待检测负载电流如图3所示，含有大量谐波以及白噪声，其THD=32.70%，基波频率为50 Hz，检测150 ms波形，在60 ms处负载电流幅值跳变为2倍，以检测各算法动态响应性能。

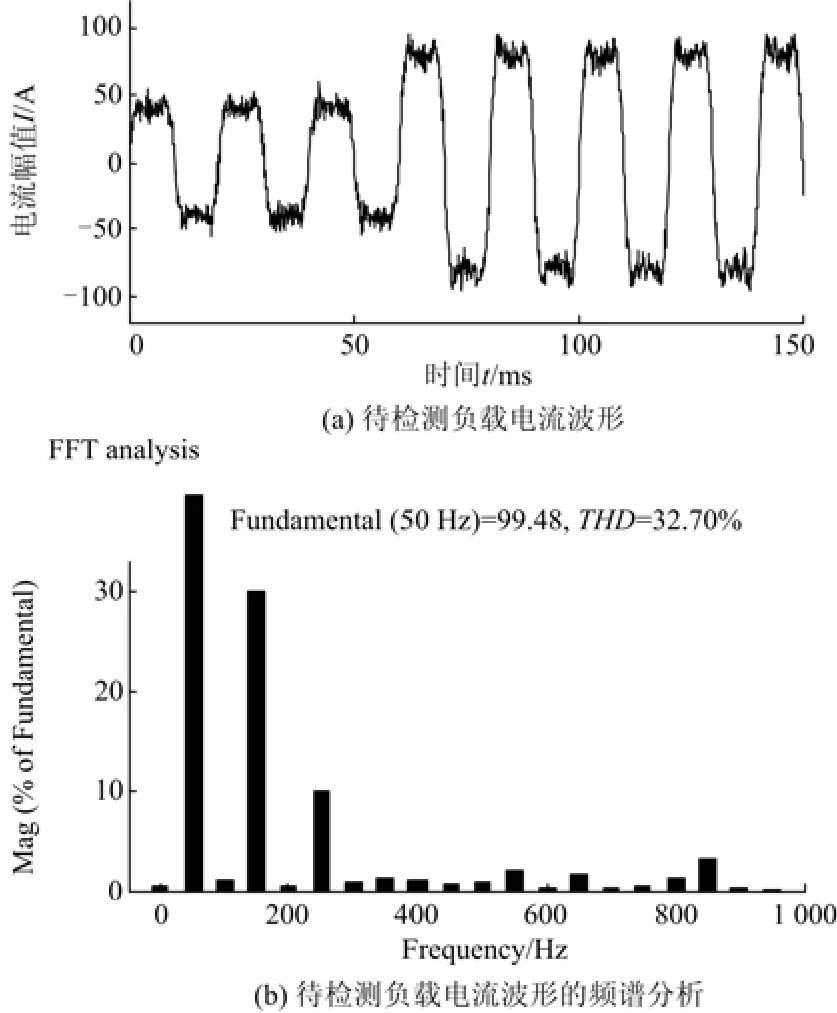
图3 待检测负载电流波形及其频谱分析Fig. 3 Waveform and frequency spectrum analysis of load current

图4 为各算法检测出的基波有功电流波形。对比可看出，改进算法在10 ms左右即跟踪上实际波形，跳变时刻，检测波形迅速跟踪上实际波形，动态响应性能优异，检测误差较为平稳，检测精度较好。而MVSS-LMS算法初始收敛时间过长，需要1.5个周期，即30 ms左右才能跟踪上实际波形，跳变时刻，检测波形基本跟踪上实际波形，动态响应性能较好，传统定步长算法跟踪速度慢，需要2.5个周期才能跟踪上实际波形，并且固定步长不能兼顾跳变前后的检测精度。

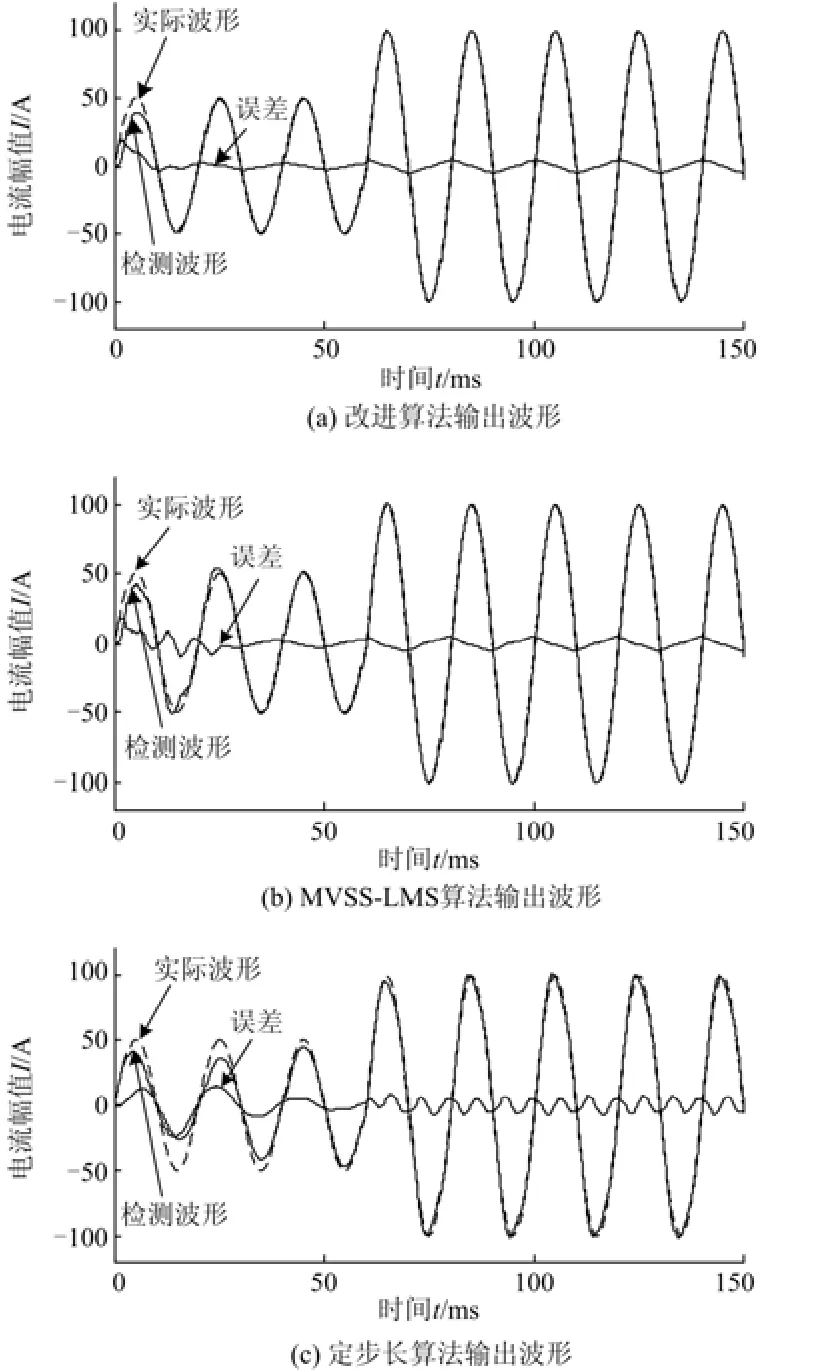
图4 各算法输出基波有功电流波形Fig. 4 Waveforms of the output fundamental active current of each algorithms

图5 为检测出的基波有功电流信号的频谱，选取各算法输出波形的第6个周期作频谱分析。改进算法输出波形的THD=0.63%，基波幅值为99.67A。MVSS-LMS算法输出波形的THD=0.67%，基波幅值为101.2A；定步长算法输出波形的THD=6.50%，谐波含量依然较高。改进算法和MVSS-LMS算法的检测精度都很好。

图6为改进算法和MVSS-LMS算法的步长变化曲线。两者初值相同，改进算法的步长在检测开始时就迅速衰减，20 ms处基本收敛，与图4(a)对照可知改进算法跟踪速度较快，收敛后能及时跟踪系统跳变，动态响应性能好。而MVSS-LMS算法的步长在前30 ms均保持为步长最大值30 ms后才开始衰减，并且衰减速度明显快于改进算法，与图4(b)对照可知，MVSS-LMS算法在初期跟踪时间较长，算法收敛后动态响应性能尚可。

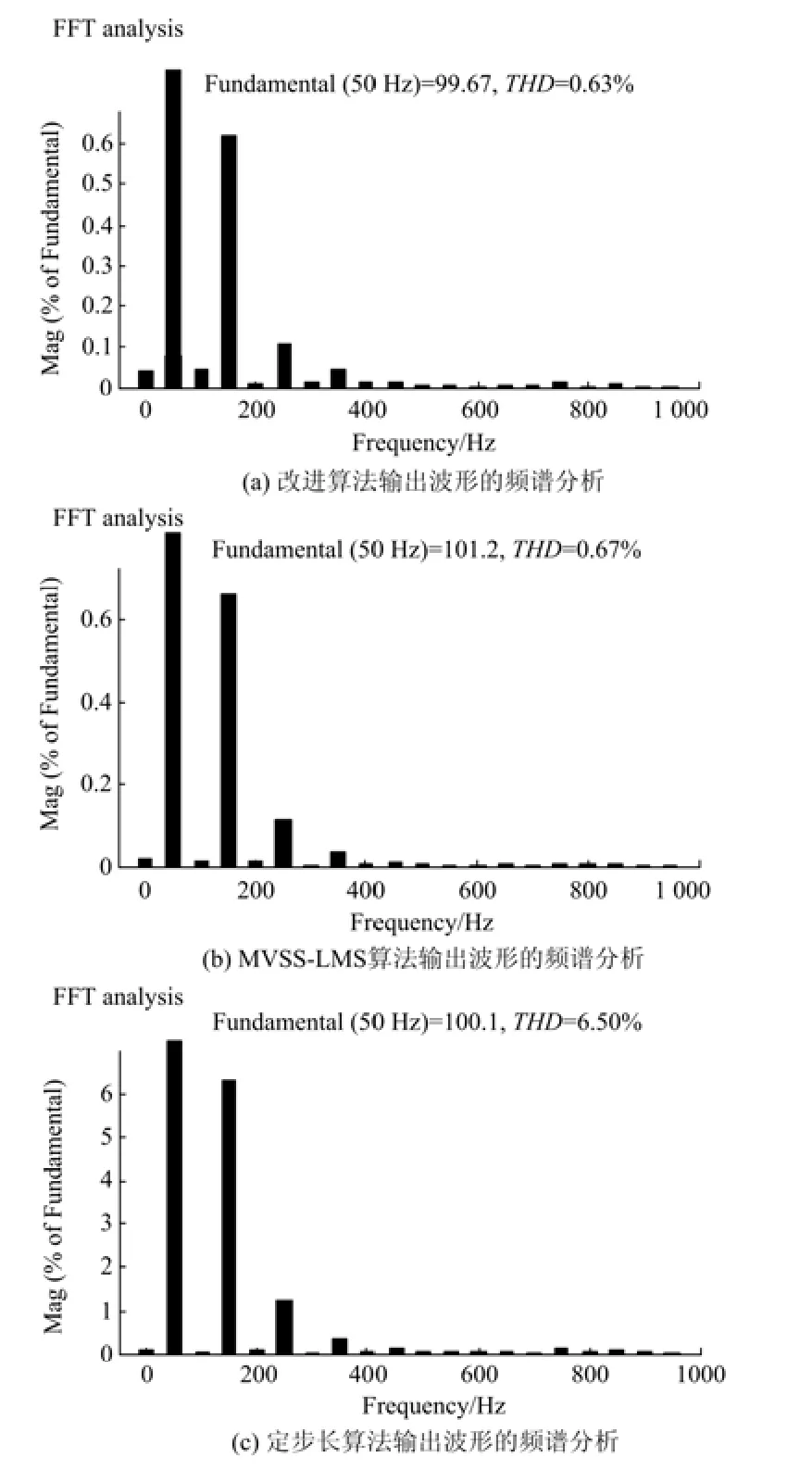
图5 各算法输出波形的频谱分析Fig. 5 Frequency spectrum analysis of output waveforms of each algorithm

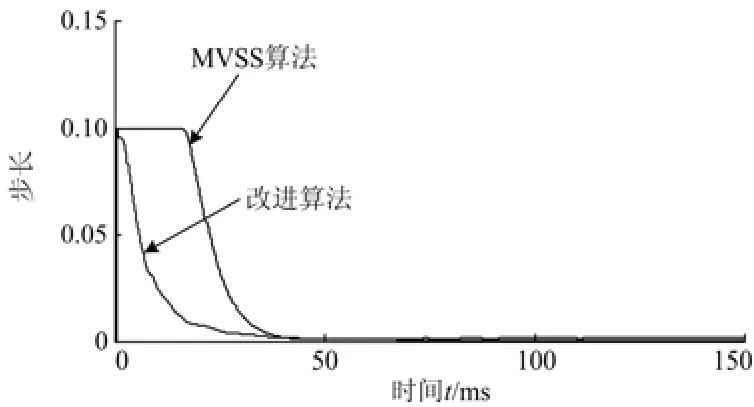
图6 步长变化曲线Fig. 6 Tracks of the steps

4 结论

本文针对APF的谐波检测问题，提出了一种改进的变步长LMS自适应谐波检测算法。改进算法在MVSS-LMS算法的基础上，将历史误差的遗忘加权和引入步长迭代，并且对步长因子作动态变化约束，避免了步长迭代后期收敛速度过快的缺陷，增强了算法的鲁棒性。实验结果表明，与参数固定条件下的定步长算法和MVSS-LMS算法相比，在输入信号的信噪比较低的情况下，改进算法提高了跟踪速度和检测精度，减小了稳态误差，验证了其在APF谐波检测中的优势。本文主要在单相系统中研究，后续会将改进算法引入三相系统，以获得更好的通用性。

[1] 刘心旸, 王杰. 基于瞬时无功功率理论的自整定因子变步长低通滤波器研究[J]. 电力系统保护与控制, 2012, 40(10): 84-89. LIU Xinyang, WANG Jie. A variable step-size low-pass filter with self-tuning factor based on instantaneous reactive power theory[J]. Power System Protection and Control, 2012, 40(10): 84-89.

[2] 翟瑞淼, 英超, 任国臣, 等. 基于 Nuttall 窗的三峰插值谐波算法分析[J]. 电力系统保护与控制, 2015, 43(10): 38-43. ZHAI Ruimiao, YING Chao, REN Guochen, et al. An approach for harmonic analysis based on Nuttall window and triple-spectral-line interpolation[J]. Power System Protection and Control, 2015, 43(10): 38-43.

[3] 孙曙光, 庞毅, 王景芹, 等. 一种基于新型小波阈值去噪预处理的EEMD谐波检测方法[J]. 电力系统保护与控制, 2016, 44(2): 42-48. SUN Shuguang, PANG Yi, WANG Jingqin, et al. EEMD harmonic detection method based on the new wavelet threshold denoising pretreatment[J]. Power System Protection and Control, 2016, 44(2): 42-48.

[4] 陈欢, 何怡刚, 肖建平, 等. 基于CWT和DWT相结合的谐波检测[J]. 电力系统保护与控制, 2015, 43(20): 71-75. CHEN Huan, HE Yigang, XIAO Jianping, et al. Harmonic detection based on a combination of continuous wavelet transform and discrete wavelet transform[J]. Power System Protection and Control, 2015, 43(20): 71-75.

[5] 李乔, 吴捷. 自适应谐波电流检测方法用于有源电力滤波器的仿真研究[J]. 电工技术学报, 2004,19(12): 86-90. LI Qiao, WU Jie. Simulation study of adaptive harmonic current detection method for active power filters[J]. Transactions of China Electrotechnical Society, 2004, 19(12): 86-90.

[6] 刘传林, 刘开培. 基于新型变步长算法的自适应三相电路谐波检测[J]. 电力系统保护与控制, 2013, 39(7): 123-128. LIU Chuanlin, LIU Kaipei. Adaptive harmonic detection of 3-phase circuits based on a novel variable step-size algorithm[J]. Power System Protection and Control, 2013, 39(7): 123-128.

[7] WANGER V E. Effects of harmonics on equipment[J]. IEEE Transactions on Power Delivery, 1993, 8(2): 672-680.

[8] 王俊杰, 郑益慧, 姚钢, 等. 有源电力滤波器的动态因子LMS谐波检测方法[J]. 电力自动化设备, 2011, 31(4): 91-95. WANG Junjie, ZHENG Yihui, YAO Gang, et. al. Dynamic factor LMS algorithm for APF harmonic detection[J]. Electric Power Automation Equipment, 2011, 31(4): 91-95.

[9] GITLIN R D, WEINSTEIN S D. On The design of gradient algorithms for digitally implemented adaptive filters[J]. IEEE Transactions on CT, 1973, 10(2): 125-136.

[10] KWONG R H, JONSTON E W. A variable step size LMS algorithm[J]. IEEE Transactions on Signal Processing, 1992, 40(7): 1633-1642.

[11] ABOULNASR T, MAYYAS K. A Robust variable step-size LMS-type algorithm: analysis and simulations[J]. IEEE Transactions on Signal Processing, 1997, 45(3): 631-639.

[12] 杨建宁, 陈捷, 关佳军, 等. 一种改进变步长的自适应谐波检测算法[J]. 电力系统保护与控制, 2011, 39(16): 40-52. YANG Jianning, CHEN Jie, GUAN Jiajun, et al. An improved variable step-size adaptive harmonic detecting algorithm[J]. Power System Protection and Control, 2011, 39(16): 40-52.

[13] 高鹰, 谢胜利. 一种变步长LMS自适应滤波算法及分析[J]. 电子学报, 2001, 29(8): 1094-1097. GAO Ying, XIE Shengli. A variable step size LMS adaptive filtering algorithm and its analysis[J]. Acta Electronica Sinica, 2001, 29(8): 1094-1097.

[14] 李辉, 吴正国, 邹云屏, 等. 变步长自适应算法在有源滤波器谐波检测中的应用[J]. 中国电机工程学报, 2006, 26(9): 99-103. LI Hui, WU Zhengguo, ZOU Yunping, et al. A variable step size adaptive algorithm applied to harmonic detection of active power filter[J]. Proceedings of the CSEE, 2006, 26(9): 99-103.

[15] FEUER A. Convergence analysis of LMS filters with uncorrelated gauss data[J]. IEEE Transactions on Signal Processing, 1985, 33(1): 220-230.

(编辑 姜新丽)

An improved variable step-size LMS adaptive harmonic detection algorithm for active power filters

LÜ Guangqiang, LIU Yu, DUAN Haijun
(College of Automation, Nanjing University of Science & Technology, Nanjing 210094, China)

A new improved variable step-size LMS algorithm is proposed in order to enhance the tracking velocity and accuracy of harmonic detection by variable step-size LMS adaptive algorithm in the low signal-noise rate (SNR) conditions of APF. Based on the MVSS-LMS algorithm, the improved algorithm adds the estimation of forgettingweighted sum of historical errors to control the step-size updating and dynamically regulate the range of step-size. Also, sliding forgetting-weighted window is introduced to reduce computational complexity. The convergence speed and steady state performance of the algorithm are analyzed. According to experimental results, this algorithm possesses faster dynamic response speed and decreases steady state errors in low SNR conditions of APF. It has the high anti-jamming capability and better effect of harmonic current detection.

APF; harmonic detection; variable step-size; least mean square; adaptive algorithm

10.7667/PSPC150846

2015-05-19；

2016-01-20

吕广强(1974-)，男，副教授，硕士生导师，研究方向为电能质量检测与治理、电力变换器的应用等；E-mail: lgqiang1008@163.com

刘 娱(1991-)，女，硕士研究生，研究方向为电能质量检测与治理；

段海军(1990-)，男，硕士研究生，研究方向为电能质量检测与治理。