ITD算法在电能质量扰动信号特征量提取中的应用

邓志勇，彭晓亮，陈 俊，唐 曲

(湖南省电网工程公司，湖南 衡阳 421000)

ITD算法在电能质量扰动信号特征量提取中的应用

邓志勇，彭晓亮，陈 俊，唐 曲

(湖南省电网工程公司，湖南 衡阳 421000)

针对电能质量扰动信号非线性特点，采用固有时间尺度分解算法(Intrinsic Time-scale Decomposition, ITD)准确快速地提取电能质量扰动信号的幅值、频率、相位、衰减因子、扰动起止时刻等特征量。首先利用固有时间尺度分解算法提取电压扰动信号的固有旋转分量(Proper Rotation Component, PRC)。然后对PRC分量进行Hilbert变换求取相位和瞬时频率，根据高频突变点得到扰动起止时刻；由包络函数得到扰动信号的幅值，并计算衰减因子。运用Matlab对单一和复合扰动信号进行仿真计算，结果表明该方法能准确地识别电能质量扰动信号的特征量，具有抗噪能力，验证了所提方法的实时性和可行性。

电能质量；扰动信号；固有时间尺度分解；瞬时频率；固有旋转分量

0 引言

随着科技的发展，用电负荷的变化以及非线性负荷的增多，电网频繁受到各种干扰使得波形发生畸变，电能质量问题突出。而功率型电子器件和基于微机处理的控制器等现代用电装置的大量使用，提高了对于电能质量的要求，因此，研究电能质量具有重要意义[1-2]。

电网中存在的电压暂升、暂降，谐波、间谐波，衰减振荡以及电压波动与闪变等电能质量问题备受关注。目前，电能质量扰动信号特征量提取与分析的方法主要有：傅里叶变换[3]、小波变换[4-6]、S变换[7-8]、数学形态学算法[9]、Prony算法[10]、希尔伯特-黄变换(Hilbert-Huang Transform, HHT)算法[11]等，这些方法在提取电能质量扰动特征参数时取得了较好的效果，但各自也存在着一定的缺陷。傅里叶变换以正弦信号为基函数，分析精度受数据窗的影响，而且不能反映衰减阻尼特性；小波变换分析非平稳、非线性信号时，时频分辨能力好，但对噪声敏感，缺乏自适应性，检测效果与分解尺度和基函数的选择有关；S变换是短时傅里叶变换和连续小波变换的结合发展起来的，缺乏自适应性，对扰动信号的时频分布考察较困难；在信号过零点突变等情况下，数学形态学方法依然具有较好的检测效果，但最大的缺点在于结构元素的选取凭借经验；Prony算法计算速度慢，受噪声影响，且不能够处理非线性信号频率突变的情况；希尔伯特-黄(Hilbert- Huang Transform, HHT)算法自适应性好，但HHT不能直接计算扰动信号的衰减因子信息，存在计算瞬时参数时端点效应严重等问题。

Frei等于2006年提出了一种分析非平稳信号的新算法—固有时间尺度分解(ITD)[12]，它是在研究经验模态分解(EMD)和局部均值分解(Local Mean Decomposition, LMD)的基础上提出的一种新的自适应时频分析方法，可以将任意复杂信号分解成若干个有实际物理意义的固有旋转(Proper Rotation Component, PRC)分量和一个残余分量，具有运算速度快，过滤噪声，时频分辨率高等特点，本文提出的ITD算法克服了EMD、LMD中存在比较严重的端点效应和虚假分量的问题[13]，适合提取电能质量扰动信号的特征量。

结合电能质量扰动信号的特点，本文给出了扰动信号参数提取方法。首先，通过固有时间尺度分解算法把电压扰动信号分解成若干个PRC分量，然后对PRC分量进行希尔伯特变换得到瞬时频率和相位，利用包络函数计算幅值和衰减因子，仿真结果表明该算法可以实现单一和复合扰动下的参数识别。

1 ITD算法基本原理

ITD算法是依据信号自身局部时间尺度的特点自适应地将信号分解成具有一定物理含义基函数，将基函数从原信号中分离出来得到若干个不同频率PRC分量和一个残余分量，其分解步骤如下[14-15]。

2) 由表达式(1)可知kL的值是从个端点1L、ML的值需进行估计计算。根据EMD中端点延拓的办法，采用镜像延拓算法将左右极值点向两端各延拓一个，得左右端极值点分别是令k分别等于0和M-1，按式(1)求出L1、

4) 将PRC1分量从原信号中分离出来，得到新的剩余信号。

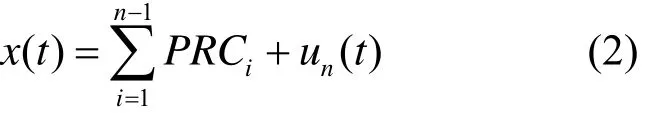
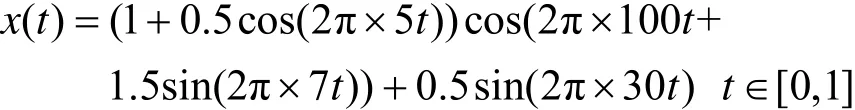
ITD和LMD算法的分解波形如图1、图2，ITD算法可以分解得到原信号中各调幅、调频PRC1、PRC2两个有效的分量和残余信号r，LMD分解得到PF1～PF5五个分量和一个残余信号r，可知，ITD分解的虚假分量比较少。从PRC2和PF2可知，ITD算法的端点效应要好于LMD算法，避免了对内部数据造成“污染”。每个PRC分量加上残余分量能准确重构原始信号表示重构信号。

图1 ITD的分解结果Fig. 1 Results of improved ITD decomposition

图2 LMD的分解结果Fig. 2 Results of LMD decomposition

2 扰动信号特征参数提取

若x(t)为随机的实信号，则希尔伯特变换[11]y(t)可定义为：

通过此变换后，x(t)和y(t)可构成一个共轭的复对数，于是，得到相应解析信号的表达式为：

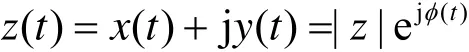
则相位函数表示为：

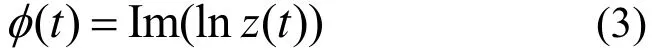
对式(3)求导得到瞬时频率表达式为：

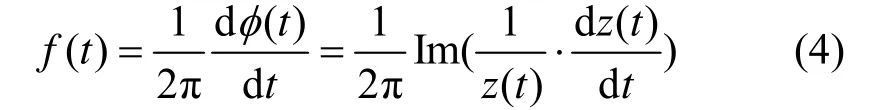
式(3)、式(4)中Im表示取虚部。

对应的幅值函数可表示为：

在电力系统中，电压扰动信号可表示成n个振荡模态之和，具体的表达式为[16]

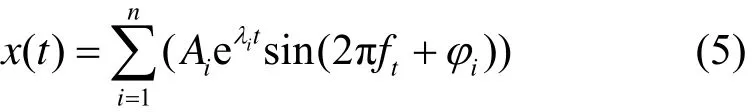
其中：Ai是振荡模态i的幅值；li是振荡模态i的衰减因子；jii是振荡模态的初始相位；fi是振荡模态i的频率。

比较式(2)、式(5)可以看出，PRCi分量和单个的振荡模态是一一对应的，看作是振荡模态i的瞬时幅值，即

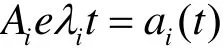
于是，计算得到瞬时阻尼为

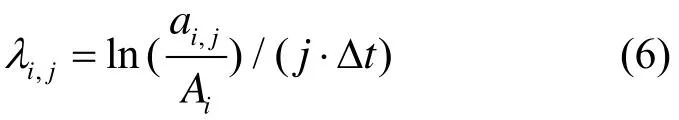
式中：,iaij为第个振荡模态在j时间点的幅值；为时间间隔。为了减小初始幅值对计算结果精确度的影响，瞬时衰减因子可以表示为：

当发生扰动时，在扰动起止时刻会产生信息突变[17]，由式(3)知，相位函数为对数函数，其值可为任意数，突变信息不会丢失，能准确定位。

为了提高算法准确度，本文对PRC分量进行Hilbert解调后再计算瞬时幅值、衰减因子、瞬时频率和相位，进而根据和衰减因子来进行电能质量扰动信号的检测与分析。

结合固有时间尺度分解和电能质量扰动信号特征参数提取步骤的流程图如图3。

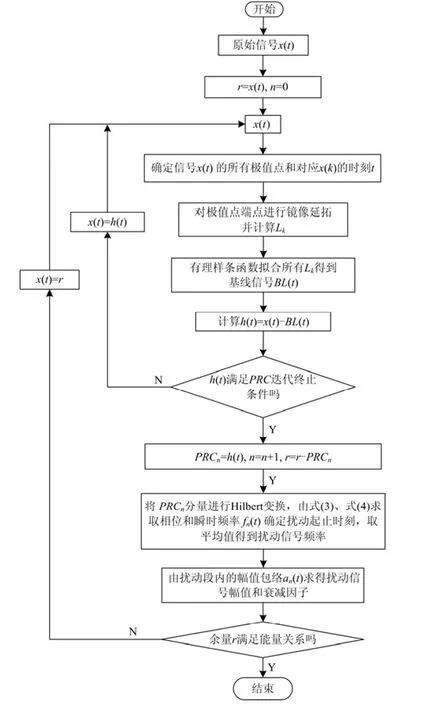
图3 算法流程图Fig. 3 Flowchart of proposed method

3 算例仿真分析

3.1 电压暂降

电压暂降信号表达式为：

式中：e为单位阶跃函数；采样频率f=3 200 Hz。

ITD分解电压暂降信号得到各个PRC分量如图4，从图4可以看出扰动信号只是幅值发生了变化，从时频图中可以看到扰动发生的起止时刻和突变频率，因此可由高频突变点确定扰动起止时刻，提取扰动段内信号求取特征参数如表1，与理论值接近。

图4 电压暂降信号分析结果Fig. 4 Decomposition results of the signal voltage dips

为了验证对含有噪声的扰动信号提取效果，在暂降扰动中加信噪比为20 dB的白噪声，得到扰动信号参数如表1所示，可见，在加入白噪声的情况下，基于ITD的扰动信号特征量提取与无噪声情况下的结果基本相同，说明ITD算法具有抗噪声干扰的能力。

电压暂升和电压中断扰动的ITD分解、检测结果与电压暂降的结果类似。

3.2 谐波扰动

电压谐波扰动信号表达式为：

ITD分解含谐波扰动的电压仿真信号如图5所示，可认为PRC1信号中出现了两种不同的谐波，且谐波发生的时刻不同，PRC2中出现了一种谐波。从PRC1、PRC2、PRC3可以看出谐波依次被分离出来，信号频率呈递减规律，每段信号的最高次谐波出现在PRC1分量中。将PRC1、PRC2分量进行Hilbert变换求取瞬时频率如图6，根据时频图中的高频突变点可以检测到扰动的起止时刻。由PRC1分量的时频图可以看出：从0.021 2 s到0.062 4 s，PRC1分量频率为150.60 Hz，从0.062 4 s到0.141 4 s，PRC1分量频率为349.87 Hz，其他时刻为基波频率；由PRC2分量的时频图可以看出：从0.021 2 s到0.062 4 s，PRC2分量频率为50 Hz，从0.062 4 s到0.141 4 s，PRC2分量频率为150.60 Hz, 其他时刻频率为0。在0.021 2～ 0.062 4 s时段原信号中仅含有3次谐波，在0.062 4～ 0.141 4 s时段原信号中含有3、7次谐波，结果与所给数学模型一致。提取扰动段内的PRC1、PRC2分量由式(3)求取扰动信号的初始相位；对于所求瞬时参数的波动性问题常采用拟合和求平均值两种方法[18]，由扰动段内的函数得到扰动信号瞬时幅值和瞬时频率，取平均值后结果如表1。

表 1 基于LMD和ITD的扰动信号参数识别结果Table 1 Disturbance signal parameter identification results based on LMD and ITD

图5 谐波扰动信号的分解结果Fig. 5 Decomposition results of harmonics

图6 PRC1、PRC2分量的瞬时频率Fig. 6 Instantaneous frequency of PRC1and PRC2component

3.3 衰减振荡

电压衰减振荡扰动信号表达式为：

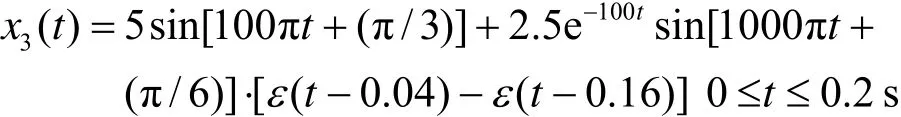
包含衰减振荡扰动的仿真信号分解如图7，图中3x(t) 为仿真信号，可认为PRC1分量包含衰减振荡分量和基波分量，PRC2只包含扰动段内的基波分量，可以看出固有时间尺度将信号分解成高频到低频的优势。从时频图可以确定扰动发生的起止时刻，提取扰动段内的信号，通过式(3)～式(7)计算衰减振荡参数如表1。

图7 衰减振荡信号的分解结果Fig. 7 Decomposition results of damped oscillations

3.4 电压闪变

电压闪变与波动信号表达式为：

ITD分解电压闪变信号得到基波包络信号及瞬时频率如图8，根据时频图中的高频突变点确定扰动段，根据扰动段内的基波包络函数提取电压闪变参数如表1。

图8 电压闪变信号分解结果Fig. 8 Decomposition results of voltage flicker

3.5 复合扰动

衰减振荡加3次谐波扰动信号表达式为：

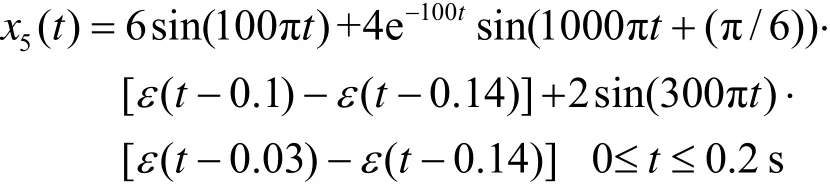
将扰动信号首先进行FFT频谱分析作为对比结果如图9所示，可以看出复合扰动信号内主要的频率点为：50 Hz、150 Hz、500 Hz。

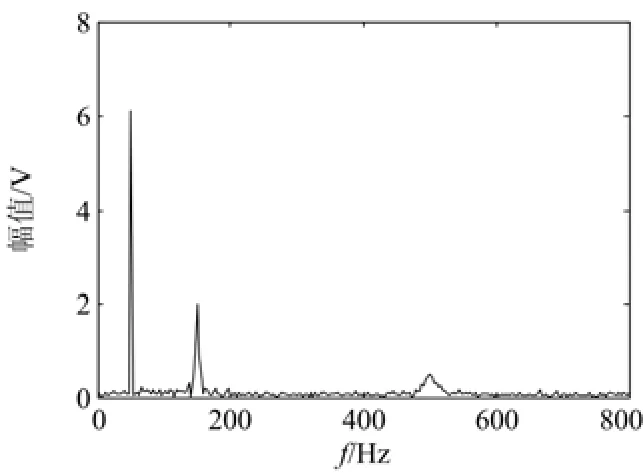
图9 复合扰动信号的FFT分析Fig. 9 Analysis of FFT for compound disturbance

将复合扰动信号进行ITD分解得到各个PRC分量如图10，对各PRC1、PRC2分量进行Hilbert变换求取瞬时频率如图11。从图10、图11中，可认为PRC1包含了3段不同频率的信号：基波信号、3次谐波信号、500 Hz衰减振荡信号；PRC2包含2段信号：基波信号、3次谐波信号，说明衰减振荡信号频率大于3次谐波频率，在扰动重叠时间内，500 Hz衰减振荡信号先被分解出来，被衰减振荡信号占据的3次谐波信号被分解在PRC2分量中，说明ITD具有良好的频率分辨能力，能够有效地提取复合扰动参数。

图10 复合扰动信号的ITD分解Fig. 10 ITD for compound disturbance

图11 PRC1、PRC2分量的瞬时频率Fig. 11 Instantaneous frequency ofPRC1andPRC2component

4 结论

针对电能质量扰动信号的非线性的特点，本文提出了一种综合性辨别方法来计算分析电能质量扰动信号的幅值、频率、相位和衰减因子等特征参数，结论如下：

1) 利用各层PRC分量Hilbert变换得到的瞬时频率可以定位单一和多重复合扰动的起止时刻，避免了LMD中直接利用调频函数计算扰动起止时刻不准的缺点；

2) 对单一和复合扰动而言，通过扰动段PRC分量得到的相位、频率以及用纯包络函数计算的幅值与衰减因子的精度都较高，理论与仿真结果表明该方法能有效、准确地提取各种电能质量扰动信号的参数，频率分辨率好，且不受噪声的影响。

[1] 刘晓胜, 刘博, 徐殿国. 基于类别语言值的电能质量信号模糊分类[J]. 电工技术学报, 2015, 30(12): 392-399. LIU Xiaosheng, LIU Bo, XU Dianguo. Fuzzy classification of power quality signals based on pattern linguistic values[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 392-399.

[2] 肖助力, 龚仁喜, 陈双. 一种改进不完全S 变换的电压暂降检测方法[J]. 电力系统保护与控制, 2015, 43(9):62-69. XIAO Zhuli, GONG Renxi, CHEN Shuang. Detection of voltage sag by a modified incomplete S-transform[J]. Power System Protection and Control, 2015, 43(9): 62-69.

[3] 高云鹏, 李峰, 陈婧, 等. 基于Teager-Kaiser能量算子Rife-Vincent窗频谱校正的电压闪变测量[J]. 电工技术学报, 2014, 29(6): 249-251. GAO Yunpeng, LI Feng, CHEN Jing, et al. Voltage flicker measurement using the Teager-Kaiser energy operator based on Rife-Vincent window spectral correction[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 249-251.

[4] 房国志, 杨超, 赵洪. 基于FFT 和小波包变换的电力系统谐波检测方法[J]. 电力系统保护与控制, 2012, 40(5): 75-79. FANG Guozhi, YANG Chao, ZHAO Hong. Detection of harmonic in power system based on FFT and wavelet packet[J]. Power System Protection and Control, 2012, 40(5): 75-79.

[5] 吴兆刚, 李唐兵, 姚建刚, 等. 基于小波和改进神经树的电能质量扰动分类[J]. 电力系统保护与控制, 2014, 42(24): 86-92. WU Zhaogang, LI Tangbing, YAO Jiangang, et al. Power quality disturbance classification based on wavelet and improved neural tree[J]. Power System Protection and Control, 2014, 42(24): 86-92.

[6] 关维国, 姚清志, 高阳, 等. 基于db4小波的配电网暂态电能质量扰动的检测与定位[J]. 电力系统保护与控制, 2015, 43(8): 102-103. GUAN Weiguo, YAO Qingzhi, GAO Yang, et al. Transient power quality detection and location of distribution network based on db4 wavelet transform[J]. Power System Protection and Control, 2015, 43(8): 102-103.

[7] 黄南天, 徐殿国, 刘晓胜. 基于S变换与SVM的电能质量复合扰动识别[J]. 电工技术学报, 2011, 26(10): 23-29. HUANG Nantian, XU Dianguo, LIU Xiaosheng. Identification of power quality complex disturbances based on S-transform and SVM[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 23-29.

[8] 郭俊文, 李开成, 何顺帆, 等. 基于改进不完全 S 变换与决策树的实时电能质量扰动分类[J]. 电力系统保护与控制, 2013, 41(22): 103-110. GUO Junwen, LI Kaicheng, HE Shunfan, et al. A real time power quality disturbance classification based on improved incomplete S-transform and decision[J]. Power System Protection and Control, 2013, 41(22): 103-110.

[9] 凌玲, 徐政. 基于数学形态学的动态电能质量扰动的检测与分类方法[J]. 电网技术, 2006, 30(5): 62-66. LING Ling, XU Zheng. Detection and location of power quality disturbance based on mathematical morphology[J]. Power System Technology, 2006, 30(5): 62-66.

[10] 王铁强, 贺仁睦, 徐东杰. Prony算法分析低频振荡的有效性研究[J]. 中国电力, 2001, 34(11): 38-41. WANG Tieqiang, HE Renmu, XU Dongjie. Prony algorithm analysis of low frequency oscillation[J]. Electric Power, 2001, 34(11): 38-41.

[11] 刘志刚, 李文帆, 孙婉璐. 希尔伯特-黄变换及其在电力系统中的应用[J]. 电力自动化设备, 2012, 32(4): 109-116. LIU Zhigang, LI Wenfan, SUN Wanlu. Hilbert-Huang transform and its applications in power system[J]. Electric Power Automation Equipment, 2012, 32(4): 109-116.

[12] FREI M G, OSORIO I. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society of London A, 2006, 463(2078): 321-342.

[13] 任达千, 杨世锡, 吴昭同. 基于LMD 的信号瞬时频率求取方法及实验[J]. 浙江大学学报 (工学版), 2009, 43(3): 523-528. REN Daqian, YANG Shixi, WU Zhaotong. Instantaneous frequency extraction method and experiment based LMD[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(3): 523-528.

[14] 郑近德, 程军圣, 杨宇. 基于改进的 ITD 和模糊熵的滚动轴承故障诊断方法[J]. 中国机械工程, 2012, 23(19): 2372-2377. ZHENG Jinde, CHENG Junsheng, YANG Yu. A rolling bearing diagnosis method based on improved ITD and fuzzy entropy[J]. China Mechanical Engineering, 2012, 23(19): 2372 -2377.

[15] 程军圣, 李海龙, 杨宇. 改进ITD和能量矩在齿轮故障诊断中的应用[J]. 振动、测试与诊断, 2013, 33(6): 954-959. CHENG Junsheng, LI Hailong, YANG Yu. Application of improved ITD and energy moment in diagnosing the gear fault[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(6): 954-959.

[16] 杨德昌, 唐巍, 屈瑞谦, 等. 基于改进局部均值分解的低频振荡参数提取[J]. 中国电机工程学报, 2013, 33(4): 135-140. YANG Dechang, TANG Wei, QU Ruiqian, et al. Extraction of the oscillatory parameters of low frequency oscillation based on improved local mean decomposition[J]. Proceedings of the CSEE, 2013, 33(4): 135-140.

[17] 宋海军, 黄传金, 刘宏超, 等. 基于改进LMD的电能质量扰动检测新方法[J]. 中国电机工程学报, 2014, 34(2): 38-40. SONG Haijun, HUANG Chuanjin, LIU Hongchao, et al. New method of power quality disturbance detection based on improved LMD[J]. Proceedings of the CSEE, 2014, 34(2): 38-40.

[18] 黄传金, 曹文思, 陈铁军, 等. 局部均值分解在电力系统间谐波和谐波失真信号检测中的应用[J]. 电力系统自动化设备, 2013, 34(9): 68-72. HUANG Chuanjin, CAO Wensi, CHEN Tiejun, et al. Local mean decomposition applied in harmonics and harmonic distortion signal detection of power system[J]. Power System Automation Equipment, 2013, 34(9): 68-72.

(编辑 周金梅)

Application of feature extraction of power quality disturbance signal using ITD

DENG Zhiyong, PENG Xiaoliang, CHEN Jun, TANG Qu
(Hunan Power Engineering Company, Hengyang 421000, China)

For non-linear characteristics of power quality disturbance signal, the characteristic parameters of power quality disturbance signal such as amplitude, frequency, phase, attenuation factor and the starting and ending time of the disturbance can be quickly and accurately extracted by intrinsic time-scale decomposition. Firstly, voltage disturbance signals are decomposed into proper rotation component (PRC) by intrinsic time-scale decomposition algorithm. To apply the Hilbert transform to get phase and instantaneous frequency of PRC components, then according to hyper mutation of instantaneous frequency, the starting and ending time of the disturbance are got; the envelope function is utilized to calculate amplitude and the attenuation factor. Utilizing Matlab, simulations of single disturbance signal and mixed disturbance signals are done and calculation results show that this method can accurately identify power quality disturbance signal parameters and anti-noise performance. The timeliness and feasibility of the proposed method is verified.

power quality; disturbance signal; intrinsic time-scale decomposition; instantaneous frequency; proper rotation component

10.7667/PSPC150811

2015-05-13；

2015-11-25

邓志勇(1979-)，男，工程师，研究方向为超特高压输电线运行检修、电力系统继电保护；E-mail: 935850757@ qq.com

彭晓亮(1980-)，男，高级工程师，主要从事特高压输电线运行检修方面研究；

陈 俊(1983-)，男，工程师，主要从事特高压输电线运行检修方面研究。