计及动态无功控制影响的大规模风电汇集地区电压稳定性分析

周红婷，宋 玮

(华北电力大学电气与电子工程学院，河北 保定 071003)

计及动态无功控制影响的大规模风电汇集地区电压稳定性分析

周红婷，宋 玮

(华北电力大学电气与电子工程学院，河北 保定 071003)

为了进一步分析大规模风电汇集地区电压稳定性，提出应考虑风电场动态无功控制的影响。基于电压-无功灵敏度法解释了动态无功补偿装置的恒无功控制方式所带来的汇集地区电压上升问题。利用小扰动稳定法，分析出采用高压侧恒电压控制的风电场内动态无功补偿装置之间存在很强的相互作用，并会引起不稳定的电压振荡。以华北某风电汇集地区为例，在PSS/E中比较分析区内所有风电场内动态无功补偿装置分别采用恒无功、高压侧恒电压和低压侧恒电压三种控制方式时受到小扰动后的电压变化。仿真结果验证了分析结论，表明在研究风电汇集地区电压稳定性问题上，考虑风电场的动态无功控制影响是必要的。

风电汇集地区；动态无功补偿方式；小扰动稳定分析；电压稳定；无功电压控制

0 引言

近年来，风电在我国迅速发展，截至2013年底，中国新增装机容量16088.7 MW，累计装机容量91412.89 MW，同比增长21.4%，两项数据均居世界第一[1]。但由于我国风电场远离负荷中心，一般大规模汇入网架结构比较薄弱的末端电网[2]，因此电压稳定性问题日益突出。针对此问题，《风电接入电网技术规定》中要求并网点电压应在额定电压的97%～107%范围内，并且并网风电场应配置无功—电压控制系统[3-4]。

众多学者在风电场无功电压控制领域展开研究，其基本思路分为两种：一是风电场的自动电压控制系统把上级调度指令转换为无功指令，在考虑风电机组的无功可调范围，SVC容量的基础上，以一定的控制策略分配给场内的无功补偿设备[5-10]；另一种则直接把调度的电压指令下发给场内动态无功补偿装置的控制器，直接调节并网点母线的电压。目前，前者已在华北、内蒙等风电汇集地区具体实施，新疆、甘肃等汇集地区则多采用后者。

以上两种控制策略带来了不同的电压稳定性问题：华北等风电汇集地区发生过风机高压脱网事故；而新疆等地区电压则经常发生高频振荡，这两种现象都对电压稳定性有很大的影响。文献[11]在分析华北某地区的一次大规模无故障高压连锁脱网事故中，指出动态无功补偿装置的恒无功控制方式会使电压-无功灵敏度增大，从而给汇集地区的电压稳定带来威胁，此研究结果说明动态无功补偿装置的控制方式可能会对风电汇集地区稳定性带来影响，但尚没有研究分析风电场中动态无功补偿装置的恒电压控制方式对电压稳定性的影响。

本文针对该问题，以动态无功补偿装置-静止无功补偿器(static var compensator，SVC)为例，在分析SVC的感性支路恒无功控制与风电汇集地区电压相互作用机理的同时，基于小干扰稳定法分析SVC恒电压控制点不同时的风电汇集地区电压稳定性，并在PSS/E中建立风电汇集系统模型，仿真SVC恒无功、低压侧恒电压及高压侧恒电压等控制方式下，受到扰动后风电场PCC母线电压变化情况，以期望所得结论能为大规模风电汇集地区无功电压控制策略的研究提供指导。

1 风电场无功电压控制策略及电压稳定性

1.1 风电场基本无功电压控制思想

目前风电场基本无功电压控制如图1所示。从图中可知，风电场的全网AVC(automatic voltage control，AVC)系统与常规能源组成的电网AVC系统[12]类似，也可认为是三级电压控制模式。

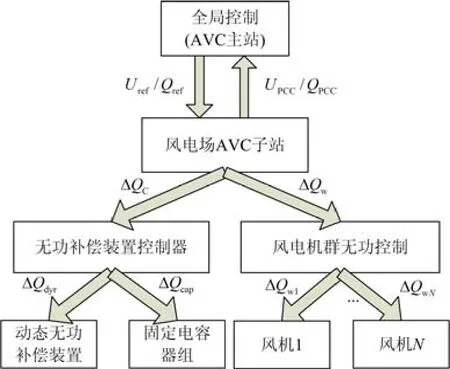
图 1 风电场无功电压控制图Fig. 1 Diagram of wind farm reactive power and voltage control

1) AVC系统的最高层为三级电压控制，它以区域内的经济运行为目标，通过各种约束条件，计算得到区域内个中枢母线的电压或无功参考值，从而下发给AVC子站，控制时间为十几分钟到小时级。

2) 风电场AVC子站为二级电压控制，其功能是通过接收到的电压或无功指令，进行无功决策，把所需的无功按照一定的原则分配给场内各类无功源，从而使风电场并网点达到电压稳定的效果。控制时间一般为秒到分钟级。

3) 一级电压控制为本地控制，主要是动态无功补偿装置和风机利用自身的控制器来进行电压控制。由于AVC子站调节电压周期在秒到分钟级，而本地控制的控制时间很快，一般为毫秒级。因此，动态无功补偿装置在执行AVC指令期间为恒无功控制。风电场中，为了减少损耗，SVC一般采用TCR+FC型。

1.2 恒无功控制方式下的电压稳定性

图2为典型的风电汇集系统图，各风电场通过35 kV/220 kV的升压变压器并入无穷大系统，场内的动态无功补偿装置SVC均接在35 kV母线上，其中系统阻抗、第i回输电线路阻抗及升压变压器阻抗分别为Xs、XLi和XTi，Bci和BLi分别表示第i个SVC感性支路和容性支路的电钠，第i个风电场发出的有功和无功分别为Pi和Qi，本文假设风机的功率因数为1，无穷大母线电压E= 1。根据此模型，基于汇集地区电压-无功灵敏度及Q-V曲线，说明SVC的恒无功控制所带来的电压稳定性问题。

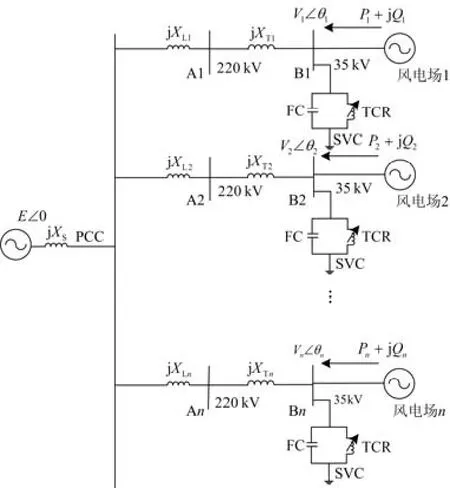
图2 典型风电汇集系统图Fig. 2 Typical equivalent system diagram of wind power integration

根据文献[11]，式(1)和式(2)分别给出第i个风电场在SVC无控制及采用感性支路恒无功控制时的电压-无功灵敏度，其中Xi=Xs+XLi+XTi，Bi=Bci-BLi。

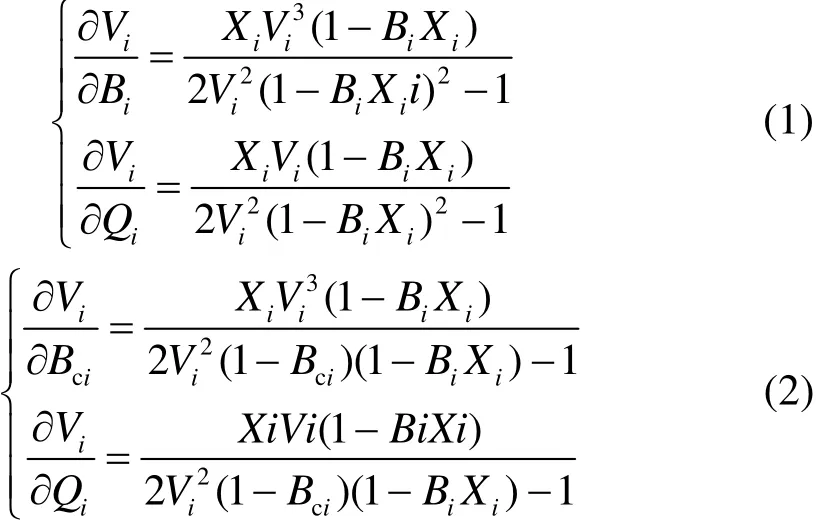
将式(1)和式(2)的分母相减得到表达式(3)：

通过此表达式可看出式(3)恒大于0，说明SVC采用恒感性支路无功控制会增大汇集母线电压无功灵敏度，增大程度取决于初始状态BLi、Bci及Xi，将式(3)表示为f(BLi,Bci,Xi),对BLi、Bci及Xi分别求导得：

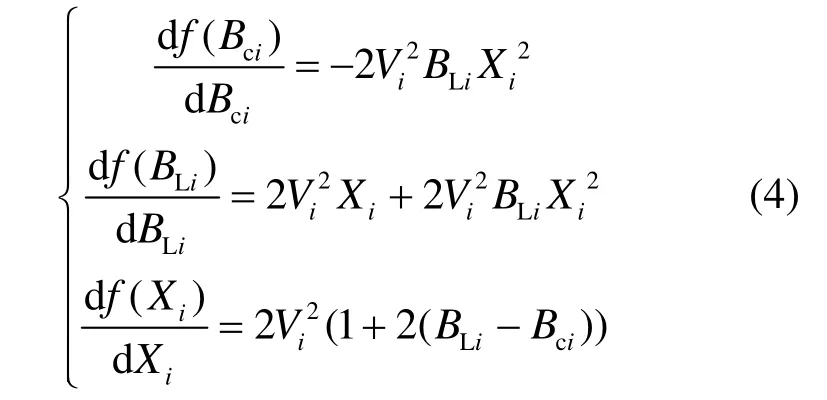
式(4)表明，母线电压无功灵敏度增大程度随Bci增大而减小，随Xi和BLi增大而增大。当风电场初始投入的Bci较小，BLi较大，且系统比较弱时，若SVC采用恒无功控制，在受到电容扰动后极易造成风机过压脱网，对系统电压稳定性带来严重影响，图3给出此情况下某风电场受到10 Mvar电容扰动，35 kV母线电压的Q-V曲线。图中A点为初始运行点，B为SVC无控制时在扰动后的电压稳定点，C点则表示SVC采用恒感性无功控制时在扰动后的电压稳定点。显然，C点已超过风机的高压限值1.1 pu。

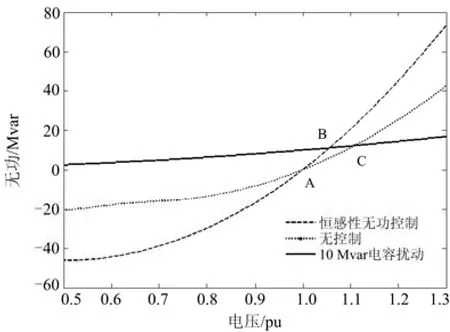
图3 10 Mvar电容扰动35 kV母线的Q-V曲线Fig. 3 Q-V curve of 35 kV bus when 10 MVar capacitance occurs in system

华北某风电汇集地区沽源地区的一次无故障风机高压连锁脱网事故正是由于动态无功补偿装置的这种控制方式，因此，需要探讨SVC的其它控制方式对电压稳定性的影响，以寻求在不同工况下较优的控制方式。

2 恒电压控制对汇集地区电压稳定性影响分析

2.1 汇集系统小扰动稳定数学模型

根据图2建立汇集系统的数学模型，图中无穷大母线可以用发电机经典二阶模型代替，SVC采用PI控制结构，其电压控制模型如图4所示，由于前面已假设风机的功率因数为1，所以分析暂不考虑风机的无功控制模型。由此，汇集系统的小干扰稳定数学模型的建立可分为以下4步。

图4 SVC恒电压控制框图Fig. 4 Constant voltage control block of SVC

1) 按照发电机节点(无穷大母线)、SVC节点、其它节点的顺序对系统所有母线编号，在汇集系 统网架结构的基础上，列出系统的网络方程如式(5)。

式中：I、U表示系统中个母线的注入电流矩阵和节点电压矩阵；Y则表示系统的节点导纳矩阵。

2) 根据汇集系统中SVC的控制模型及无穷大系统的等效模型，得到汇集系统内动态元件的动态方程及输出方程式(6)～式(9)。

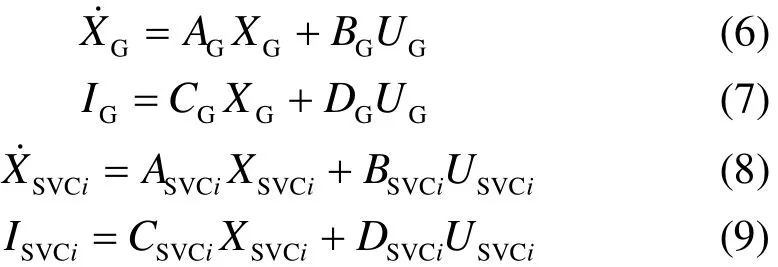
3) 对式(5)～式(9)分别线性化，并把式(6)～式(9)代入式(5)，得到全系统的线性化微分方程：

4) 根据式(10)，得出计及SVC控制方式的汇集系统的状态矩阵式(11)：

2.2 基于小扰动稳定法的汇集地区电压稳定性分析

假设汇集系统内(拓扑结构图如图2)含4个双馈风电场，基准容量为100 MVA。每个风电场配有一套TCR+FC的SVC，无功容量均为-20-20 Mvar。风电场装机容量及各风电场主变高压侧、低压侧与汇集母线的电气距离如表1所示，系统阻抗为0.05 pu。

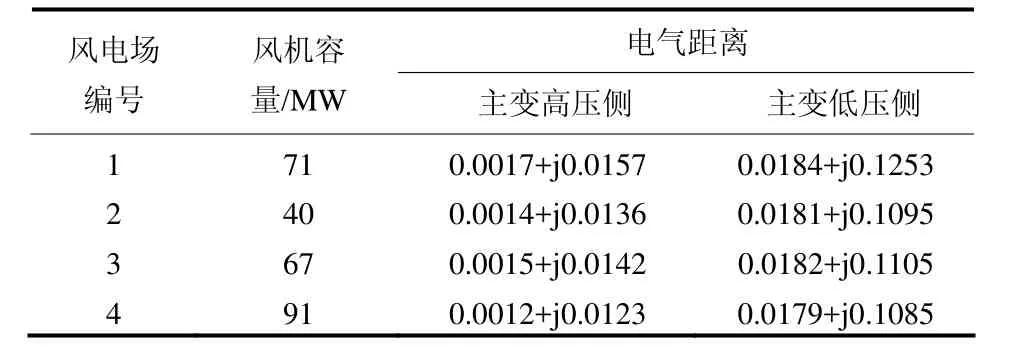
表1 各风电场电气参数Table 1 Electrical distance parameters of wind farms

当汇集系统中风电场1、2均投入高压侧恒电压控制方式下的SVC时，系统的特征根如表2所示。

表2 两风场SVC高压侧恒电压控制时系统特征根Table 2 System eigenvalue when SVC in two wind farms both control system side bus voltage

表2中，由于特征计算的误差，8l可当做系统的零特征根处理[13]，因此，在此工况下系统是稳定的，其振荡模态为2,1l。若把SVC的控制方式改为恒无功控制时，系统的特征根如表3所示。

表3 两风场SVC恒无功控制时系统特征根Table 3 System eigenvalue when SVC in two wind farms both take constant reactive power control

表3中，系统出现两个振荡模态2,1l和4,3l，对比表2，说明两种控制方式下的SVC具有不同的特性。表4利用参与因子[14]对这两种控制方式的振荡模态进行分析。

表4中，状态量1～2表示等效为无穷大系统的发电机经典二阶模型的状态量dD、wD；3～5表示系统中第1个SVC的状态量，6～8则表示第二个SVC的状态量。从表中可以看出SVC采用高压侧恒电压控制时，振荡模态与两个SVC的状态量都有关，而采用恒无功控制时，第一个振荡模态主要与第1个SVC的状态量有关，第二个振荡模态主要与第2个SVC的状态量有关。这说明SVC采用高压侧恒电压控制时，SVC之间存在较强的相互作用，而当其采用恒无功控制方式时，SVC之间几乎不存在相互作用。

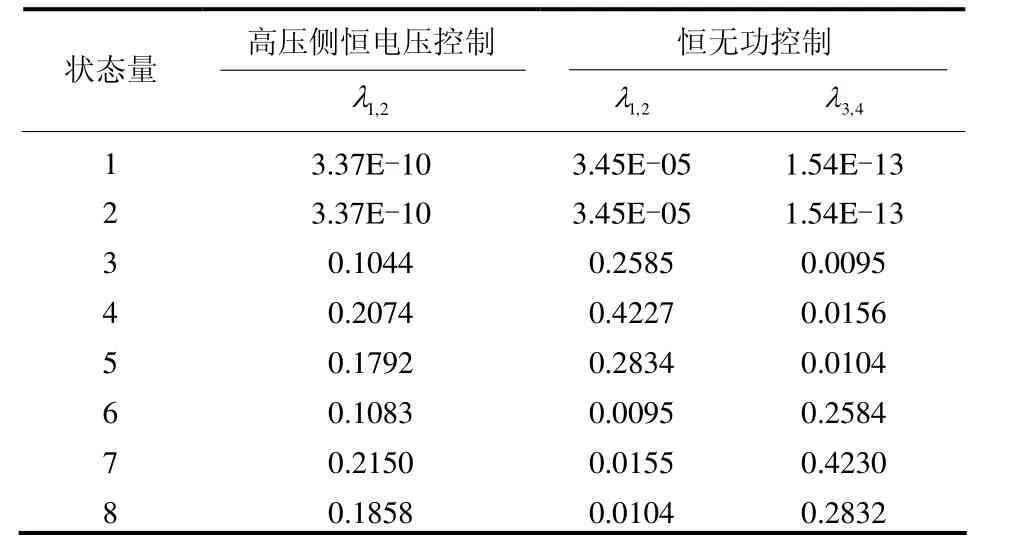
表4 SVC不同控制方式下模态分析中的参与因子Table 4 Participation factor in modal analysis when SVC takes different control modes

当SVC采用低压侧恒电压控制时，其振荡模态与采用高压侧恒电压控制时类似，但由于采用低压侧作为反馈信号，SVC之间的电气距离增大，且增大了SVC控制器模式的阻尼[15]，因此，此控制方式下的SVC之间的相互作用减弱，系统电压也更稳定。图5分别给出SVC采用高压侧恒电压、低压侧恒电压及恒无功控制方式时，系统振荡模态2,1l随投入三种控制方式下SVC的风电场个数变化的根轨迹。从图中可以看出，当投入SVC的风电场个数增多时，三种控制方式下系统的振荡模态2,1l实部均会右移，振荡频率升高；但高压侧恒电压控制时2,1l实部变化最大，振荡频率升高最多；相反，恒无功控制方式2,1l实部与振荡频率变化均最小。从此角度可分析出，SVC在高压侧恒电压控制方式下其相互作用最强，在恒无功控制方式下其相互作用最弱，而在低压侧恒电压控制方式下其相互作用介于两者之间。

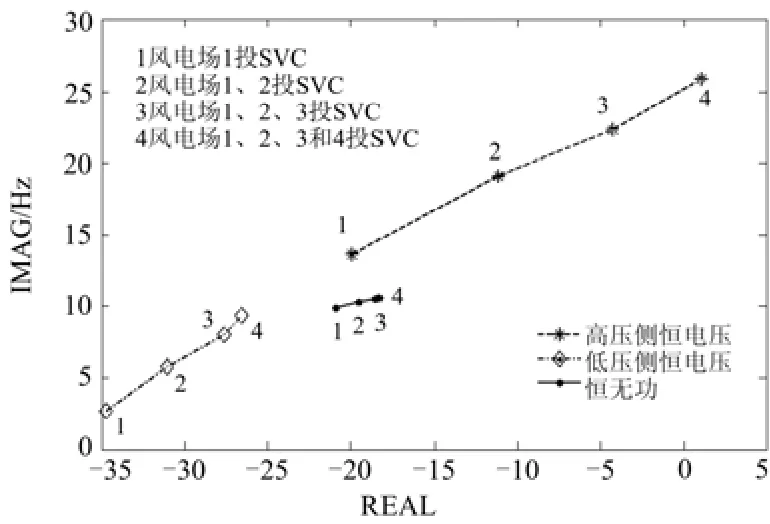
图 5 SVC不同控制方式下的根轨迹Fig. 5 System root locus when SVC takes different control modes

3 仿真算例

本文以华北某风电汇集地区为例，其拓扑结构图如图2，图中Xs表征系统强度，区内各风场的电气量如表1，在PSS/E中对以上的分析结果进行仿真验证。

汇集系统中风电场1、风电场2、风电场3、风电场4依次投入SVC，其均分别采用高压侧恒电压、低压侧恒电压及恒无功控制方式，0.1 s时系统侧投入10 Mvar电容器后，PCC母线电压变化曲线分别如图6～图8所示。

图 6 SVC控主变高压侧PCC母线电压Fig. 6 PCC bus voltage when SVC controls system side bus

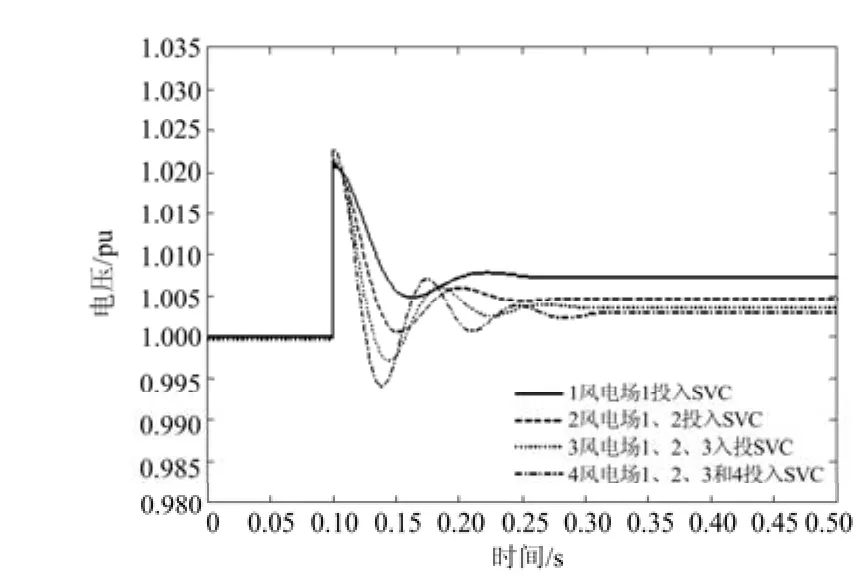
图7 SVC控主变低压侧PCC母线电压Fig. 7 PCC bus voltage when SVC controls wind farm side bus

图8 SVC恒无功控制PCC母线电压Fig. 8 PCC bus voltage when SVC takes constant reactive power control

从以上3图中可以看出：

(1) 对比图6、图7两图，在系统受到电容扰动后，SVC采用高压侧恒电压控制时，随投入SVC风电场个数的增加，电压振荡越来越严重，当汇集系统中4个风电场的SVC全部投入时，出现不稳定电压振荡，而SVC采用低压侧恒电压控制时，系统的稳定性明显优于前者。

(2) 图8中，在风电场1～4依次投入后，电压振荡趋势没有明显变化，说明SVC在此种控制方式下相互作用较弱，但图8中曲线表示系统在受到电容扰动后，电压继续上升，说明SVC恒无功控制方式会给系统带来过压问题，结合式(3)、式(4)，图9给出当系统变弱(Xs为0.15 pu)，SVC投入的初始感性无功较大(0.4 pu)时,汇集系统PCC及B1母线电压，可以看出，35 kV母线电压在控制方式的影响下已超过1.1 pu,而这会引起大规模风电机组高压脱网。

通过此仿真算例，验证了以上的分析结果。

图9 Xs=0.15 pu SVC恒无功控制，PCC及低压侧母线电压Fig. 9 PCC and wind farm side bus voltage when SVC takes constant reactive power control,Xs=0.15 pu

4 总结

本文根据目前大多数风电场的无功-电压控制现状，利用电压-无功灵敏度法分析此种控制所带来的电压稳定问题，随后基于小扰动稳定法分析风电场内的动态无功补偿装置采用恒电压控制时的电压稳定性，得到以下结论：

1) 动态无功补偿装置的恒感性无功控制在系统侧受到电容扰动后会造成汇集母线电压上升，其上升程度取决于系统强度、动态无功补偿装置的初始感性及容性无功三个因素，在系统较弱且场内动态无功补偿装置的初始感性无功较大且场内容性无功较小时，很容易造成风机高压脱网事故。但从小扰动稳定分析上看，多个风场内恒无功控制方式下的动态无功补偿装置之间相互作用弱。

2) 各风场的动态无功补偿装置采用恒电压控制方式时，系统的电压稳定性因电压控制点选取不同而不同，特别是在汇集站下有多个风电场时，高压侧恒电压控制下的动态无功补偿装置存在很强的相互作用并会引起不稳定的电压振荡，而低压侧恒电压控制方式下的动态无功补偿装置之间的相互作用则相对较弱，系统的稳定性也相对更优。

上述两条结论可以对不同风电汇集地区动态无功补偿装置控制方式的选择提出指导性的意义，为设计风电汇集地区的无功电压控制策略打下基础。

[1] 吴涛. 风电并网及运行技术[M]. 北京: 中国电力出版社, 2013.

[2] 张元, 郝丽丽, 戴嘉祺. 风电场等值建模研究综述[J].电力系统保护与控制, 2015, 43(6): 138-146. ZHANG Yuan, HAO Lili, DAI Jiaqi. Overview of the equivalent model research for wind farms[J]. Power System Protection and Control, 2015, 43(6): 138-146.

[3] 孙荣富, 张涛, 梁吉. 电网接纳风电能力的评估及应用[J]. 电力系统自动化, 2011, 35(4): 70-76. SUN Rongfu, ZHANG Tao, LIANG Ji. Evaluation and application of wind power integration[J]. Automation of Electric Power Systems, 2011, 35(4): 70-76.

[4] 李俊峰. 2012中国风电发展报告[M]. 北京: 中国环境科学出版社, 2012.

[5] 许晓菲, 牟涛, 贾琳, 等. 大规模风电汇集系统静态电压稳定实用判据与控制[J]. 电力系统自动化, 2014, 38(9): 15-19. XU Xiaofei, MU Tao, JIA Lin, et al. Practical criteria of static voltage stability in power systems with high wind penetration[J]. Automation of Electric Power Systems, 2014, 38(9): 15-19.

[6] 乔颖, 鲁宗相, 徐飞. 双馈风电场自动电压协调控制策略[J]. 电力系统自动化, 2010, 34(5): 96-101. QIAO Ying, LU Zongxiang, XU Fei. Coordinative strategy for automatic voltage control of wind farms with doubly-fed induction generators[J]. Automation of Electric Power Systems, 2010, 34(5): 96-101.

[7] 王成福, 梁军, 张利, 等. 基于静止同步补偿器的风电场无功电压控制策略[J]. 中国电机工程学报, 2010, 30(25): 23-28. WANG Chengfu, LIANG Jun, ZHANG Li, et al. Reactive power and voltage control strategy for wind farm based on STATCOM[J]. Proceedings of the CSEE, 2010, 30(25): 23-28.

[8] 刘皓明, 唐俏俏, 朱凌志, 等. 双馈型风电场参与电压无功调节的分层控制方案[J]. 电力系统保护与控制, 2014, 42(24): 79-85. LIU Haoming, TANG Qiaoqiao, ZHU Lingzhi, et al. Hierarchical control strategy of voltage and reactive power for DFIG wind farm[J]. Power System Protection and Control, 2014, 42(24): 79-85.

[9] 乔颖, 陈惠粉, 鲁宗相, 等. 双馈风电场自动电压控制系统设计及应用[J]. 电力系统自动化, 2013, 37(5): 15-22. QIAO Ying, CHEN Huifen, LU Zongxiang, et al. Design and application of automatic voltage control system in doubly-fed induction generator[J]. Automation of Electric Power Systems, 2013, 37(5): 15-22.

[10] 赵霞, 王倩, 邵彬, 等. 双馈感应风力发电系统低电压穿越控制策略研究及其分析[J]. 电力系统保护与控制, 2015, 43(16): 57-64. ZHAO Xia, WANG Qian, SHAO Bin, et al. Low voltage ride through control strategy and its analysis of doubly fed induction generator [J]. Power System Protection and Control, 2015, 43(16): 57-64.

[11] 谢欢, 吴涛, 赵亚清, 等. 计及动态无功影响的大规模风电机组高电压脱网原因分析[J]. 电力系统自动化, 2015, 39(4): 19-25. XIE Huan, WU Tao, ZHAO Yaqing, et al. Analysis on high-voltage trip-off causation of large-scale wind turbines considering the impact of dynamic reactive power control[J]. Automation of Electric Power Systems, 2015, 39(4): 19-25.

[12] 周宇华, 翟伟翔, 马平. 火电厂自动电压控制(AVC)系统方案设计[J]. 电力系统保护与控制, 2012, 40(9): 128-145. ZHOU Yuhua, ZHAI Weixiang, MA Ping. Design of automatic voltage control (AVC) system for thermal power plant[J]. Power System Protection and Control, 2012, 40(9): 128-145.

[13] 王锡凡, 方万良, 杜正春. 现代电力系统分析[M]. 北京: 科学出版社, 2003.

[14] ROGERS G. Demystifying power system oscillations[J]. IEEE Computer Application in Power, 1996, 9(3): 30-35.

[15] 徐政. 基于晶闸管的柔性交流输电控制装置[M]. 北京:机械工业出版社, 2009.

(编辑 张爱琴)

Analysis on voltage stability in large-scale wind farms integration area considering impact of dynamic reactive power control

ZHOU Hongting, SONG Wei
(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

In order to analyze voltage stability in large-scale wind farms integration area, this paper proposes that dynamic reactive power control should be considered. Presently, dynamic reactive power compensation device in wind farms widely adopts constant reactive power control. According to it, this paper firstly proposes this control mode of dynamic reactive power compensation device can bring voltage stability problem based on voltage-reactive power sensitivity method; then it uses small signal stability analysis method, consulting that there is a strong interaction between dynamic reactive power compensation devices in wind farms which adopts high-voltage side constant voltage control. As a result, it will lead to unstable high frequency oscillation; finally, taking a wind farm integration area in North China, it obtains the voltage change of all dynamic reactive power compensation device in wind farm after small disturbance when constant control mode, high-voltage side constant voltage control, and low-voltage side constant voltage control are adopted respectively. The result shows that considering dynamic reactive power control is important for voltage stability analysis in large-scale wind farms integration area.

wind farm integration area; dynamic reactive power compensation; small signal stability analysis; voltage stability; reactive power and voltage control

10.7667/PSPC150940

2015-06-05；

2015-08-27

周红婷(1990-)，女，通信作者，硕士研究生，研究方向为电力系统稳定分析与新能源无功电压控制等领域；E-mail: bleachwin2014@163.com

宋 玮(1963-)，男，博士，教授，研究方向为电力系统继电保护与稳定分析。E-mail: songwei8188@126.com