基于二维云模型同步发电机PID励磁系统仿真

李宗泽，史成军

(大连海事大学轮机工程学院，辽宁 大连 116026)

基于二维云模型同步发电机PID励磁系统仿真

李宗泽，史成军

(大连海事大学轮机工程学院，辽宁 大连 116026)

云模型可以实现定性概念与定量之间的转换，集成了概念的模糊性与随机性，可以解决非线性与不确定性问题。针对船舶电力系统中励磁系统非线性、时变性、不确定性的特点，将云模型应用到同步发电机励磁控制中，设计出二维云模型PID励磁控制器。其过程是将同步发电机端电压差及其变化率进行概念表示，形成前件二维云模型，然后根据PID三个参数信息构造成后件云模型，并制定出二维云模型双条件多规则的映射语言形式，实现对PID参数的模糊推理自整定。与可控相复励无刷励磁系统进行对比，仿真实验结果表明了二维云模型PID励磁控制系统模型具有更好的鲁棒性和自适应能力。

同步发电机；励磁；相复励；二维云模型；控制；仿真

0 引言

船舶电力系统需要具有静态稳定性和动态稳定性，所以励磁系统要保持发电机端电压的恒定和无功调节。船舶电力系统相比陆地上大电网线路短，船舶电站容量小，时间常数小，变化频繁，结构工况多变，具有非线性、时变性的特点。船舶上大多数采用无刷励磁系统[1-6]。

可控无刷励磁系统可以看成是常规的PID励磁调节器，响应端电压的变化，容易实现稳态无静差控制[7]。此时可控无刷励磁系统自适应能力较差，不能对发电机端电压进行精确地控制。贺徽等人将Mamdani模糊控制与PID相结合，设计出PID控制器，应用到同步发电机励磁控制中。与传统PID励磁控制相比较，改善了励磁控制系统的品质[8]。揭海宝等人设计出变论域同步发电机模糊PID励磁控制器，通过选择合适的伸缩因子对控制论域进行实时调整[9]。

从云模型的提出到现在，已经运用到很多领域。阎高伟等人利用云模型理论建立一种新的球磨机料位的测量模型，通过试验对比证明该模型具有很好的实用性[10]。王迎超等人通过正态云模型，实现了岩爆烈度与评价指标之间的不确定性映射，实验结果表明该模型具有较高的准确性和可靠性[11]。李志民等人运用云模型设计出同步发电机励磁控制器，显现出很好的鲁棒性，但是只考虑了电压偏差因素，属于一维云模型，忽略了端电压差变化率这一因素[12]。本文运用云模型理论，设计出二维云模型PID控制器，并应用于同步发电机励磁系统中对比，仿真后表明了二维云模型PID励磁控制器在具有不确定性的船舶电力系统中具有更好的鲁棒性和自适应性。

1 二维云模型原理

在模糊理论中，常常用隶属度来描述模糊性，但是如果隶属度函数确定后，就是用精确的数学方法去计算，缺少了随机性，不再属于模糊概念的范畴。云理论是在模糊理论的基础上提出来的，在原有的隶属度上，具有概率意义下的隶属度分布,融合了模糊性和随机性。对于任意一个e∈U，(U是一个论域)，e到区间[0,1]上的映射不再是一个固定的数值，而是一个概率分布。

云是由许多云滴所组成的。云滴之间是没有次序性的，云滴的个数越多，越能反映定性概念的整体特征。云模型体现了自然语言中概念不确定性的特点，将定性概念和定量值之间进行互相映射，用定量值去实现转换用自然语言表示的定性概念。通常用期望Ex、熵En和超熵He三个特征常数来描述正态云。期望Ex是指最能够代表定性概念的云滴，表示这些云滴在所在论域空间里分布的期望。熵En反映了在论域空间中可以被定性概念接受云滴的范围，也反映了云滴整体的离散程度。这个数字特征反映了定性概念的随机性与模糊性之间的关联性。超熵He是熵的熵，由熵的数字特征所决定。

定义1：设U是一个用精确数值表示的二维定量论域，BT(x)是U到闭区间[0，1]的映射。对于任意x∈U，都存在稳定倾向的随机数BT(x)。

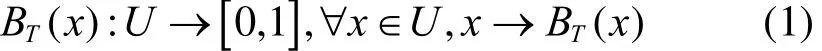
定义2：设N(Ex，Ey，Enx，Eny)表示服从二维正态随机函数。Ex，Ey是均值，Enx，Eny是熵，Hex，Hey是超熵。满足以下三个式子的云滴(xi,yi,ui) (i=1, 2, …,n)构成的云模型称为二维正态云模型。

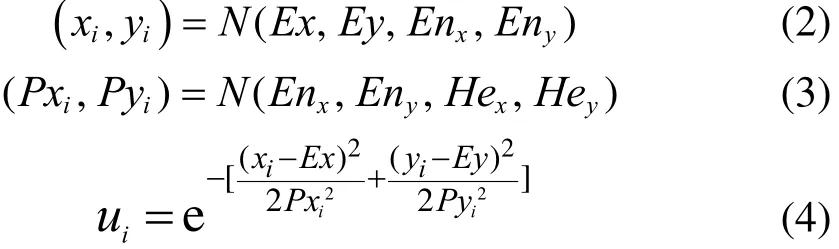
由于正态分布在概率理论中是最重要的分布之一，而且钟形隶属函数又是模糊集合中使用广泛的隶属函数，所以选用正向正态云发生器经过映射生成云滴。

二维正态云发生器算法

输入：二维云的数字特征(Ex，Ey，Enx，Eny，Hex，Hey，n)；

输出：云滴可表示为(xi,yi,ui)，i=1, 2, …,n。

算法步骤

(1) 产生一个期望值为(Enx，Eny)，方差为(Hex2，Hey2)的二维正态随机数(Pxi，Pyi)；

(2) 产生一个期望值为(Ex，Ey)的二维正态随机数(xi，yi)；

(3) 通过方程(1)计算出不确定度ui；

(4) 将(xi，yi，ui)作为一个云滴；

(5) 重复步骤(1)到(4)直到发生器产生n个云滴为止。

二维正向正态云发生器如图1。

图1 二维正向正态云发生器Fig. 1 Two dimensional positive normal cloud generator

云模型控制器主要包括三个环节：前件云发生器、规则发生器和后件云发生器。前件云发生器可以是一维的也可以是多维的，后件云发生器都是一维的。规则发生器中可以有多种规则形式：单条件单规则，双条件单规则，多条件单规则，单条件多规则，双条件多规则，多条件多规则。

2 同步发电机励磁系统数学模型

2.1 同步发电机五阶模型及静态负载模型

采用标幺制，对d轴，q轴进行等效计算。在凸极理想电机中，忽略定子绕组暂态，但计及阻尼绕组D、Q以及励磁绕组暂态和转子动态[13]。

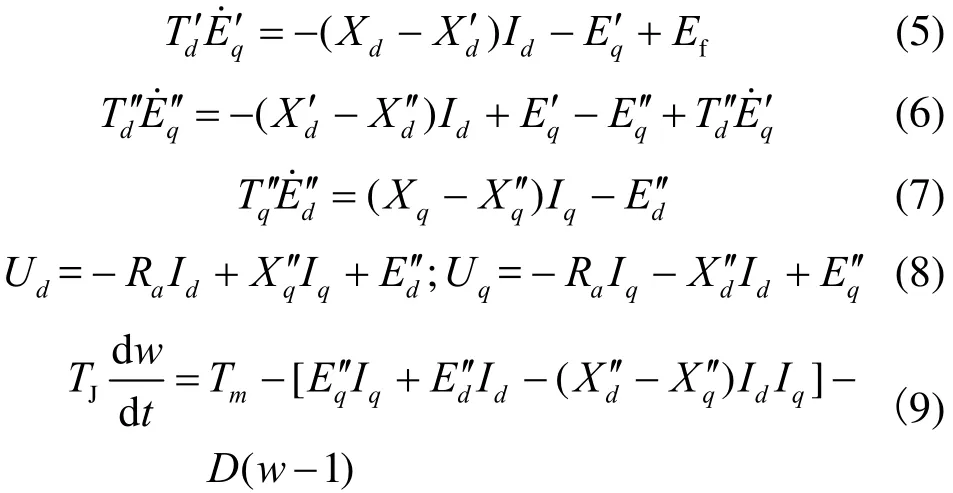
为了将负载试验简单化，可以将负载假设成三相对称串联电阻与电感的组合阻抗，用dqo坐标轴可以表示为

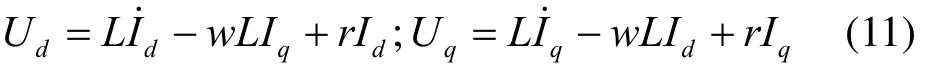
2.2 可控无刷相复励励磁系统模型

自励与复励分量经电流叠加后通过整流环节供给无刷励磁机的励磁绕组，负载电流变化时，励磁机的励磁电流随之变化，调整动态电压。再由反馈的电压差信号经过电压调整器后实现静态电压调整，进一步提高电压调整的精度。可控励磁系统流程图如图2。

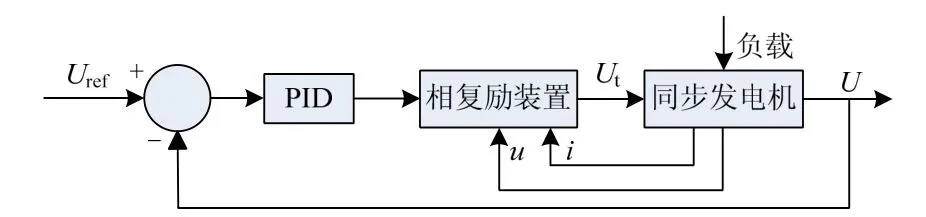
图2 可控无刷相复励励磁系统Fig. 2 Controllable phase compound excitation brushless excitation system

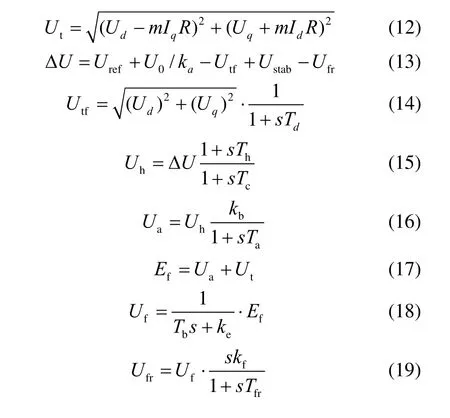
式中：Ut为相复励装置输出电压；m为电压和电流分量系数；R为移向电抗；Uref为自动调压装置参考电压；Ustab为接地电压；U0为励磁电压初始值；ka为交流无刷励磁机有效增益；Td为低通滤波器时间常数；Ufr为反馈环节输出电压；DU为综合电压偏差信号；Uh为补偿器输出电压；Th为补偿器超前补偿时间常数；Tc为补偿器滞后补偿时间常数；Ua为放大器输出电压；kb为放大器增益；Ta为放大器时间常数；Efr为调压装置输出电压；Uf为交流无刷励磁机电压；ke为交流励磁机放大系数；Tb为交流无刷励磁机时间常数；kf为反馈环节增益；Tfr为反馈环节时间常数。

3 二维云模型PID励磁系统

二维云模型PID控制器的前件云发生器的输入端是同步发电机的端电压与参考电压的差值E和电压偏差变化率EC，后件云发生器的输出端是PID的Kp,n+1,Ki,n+1,Kd,n+1的当时参数，在云规则发生器中，根据已制定的云推理规则，对PID的三个参数进行适时控制[14-16]。

二维云模型PID励磁控制器的原理流程图如图3。

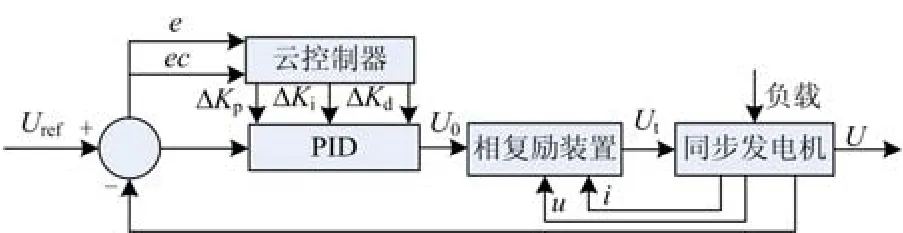
图3 二维云模型PID励磁控制器Fig. 3 Two dimensional cloud model of PID excitation controller

采用双条件多规则推理，其流程图如图4。

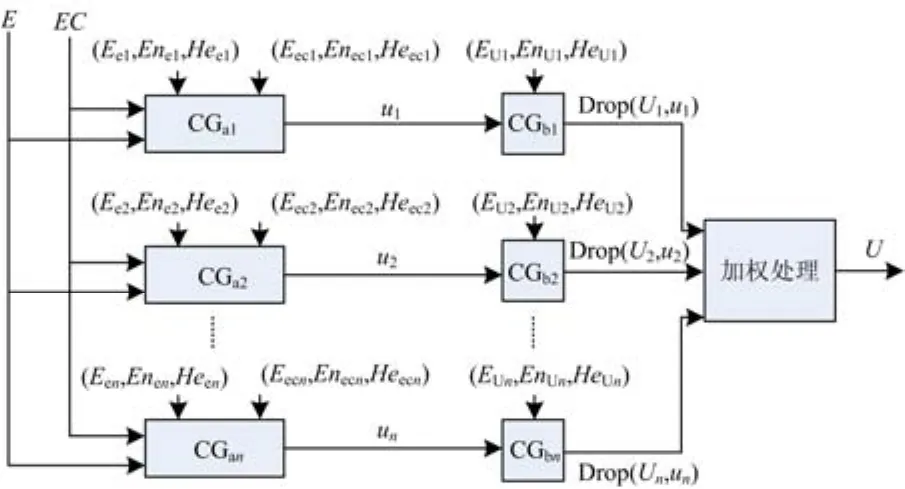
图4 双条件多规则推理Fig. 4 Double condition multi-rule inference

在前件正向正态云发生器中，偏差E(单位：伏)的正态云模型：E1=“偏差正大”(PB)=(6，0.5，0.04)；E2=“偏差正中”(PM)=(4，0.5，0.04)；E3=“偏差正小”(PS)=(2，0.5，0.04)；E4=“偏差为零”(Z)=(0, 0.5，0.04)；E5=“偏差负小”(NS)=(-2，0.5，0.04)；E6=“偏差负中”(NM)=(-4, 0.5，0.04)；E7=“偏差负大”(NB)=(-6, 0.5，0.04)；在前件云发生器中，电压偏差变化率EC与E的正态云模型相同。在后件正态云发生器中，控制量Up(单位：V)的正态云模型：Up1=“控制量正大”(PB)=(3，0.5，0.01)；Up2=“控制量正中”(PM)=(2，0.5，0.01)；Up3=“控制量正小”(PS)=(1，0.5，0.01)；Up4=“控制量为零”(Z)=(0，0.5，0.01)；Up5=“控制量负小”(NS)=(-1，0.5，0.01)；Up6=“控制量负中”(NM)=(-2，0.5，0.01)；Up7=“控制量负大”(NB)=(-3，0.5，0.01)。

在后件正态云发生器中，控制量Ui、Ud与Up的正态云模型相同。变量隶属云图如图5和图6。

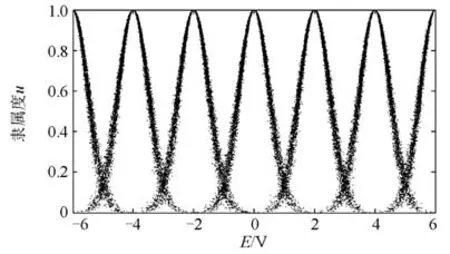
图5 E、EC隶属云Fig. 5 Membership cloud ofEandEC

图6 Up、Ui、Ud隶属云Fig. 6 Membership cloud ofUp,UiandUd

在规则发生器中，构成二维云模型的语言规则为：IfE=EtandEC=ECjthenUp=Upm,其中t,j,m=1,2,…，7。例如：IfE=E1andEC=EC3thenUp=Up6，则表示为：如果偏差E正大，而且偏差变化率EC正小，那么控制量Up则为控制量负中。控制量Ui、Ud的云模型在规则发生器中的语言规则形式与控制量Up相同。

二维云模型PID控制器的输出量Up、Ui、Ud分别对PID三个参数Kp、Ki、Kd进行实时控制，从而PID三个参数Kp、Ki、Kd能够实现自动调整，具有自适应性：

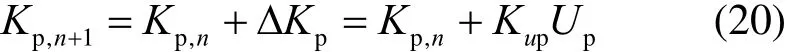
式中：Kp,n,Ki,n,Kd,n为二维云模型PID控制器的参数；Kp,n+1,Ki,n+1,Kd,n+1为二维云模型PID控制器的当时参数。

二维云模型PID控制器输出的u为

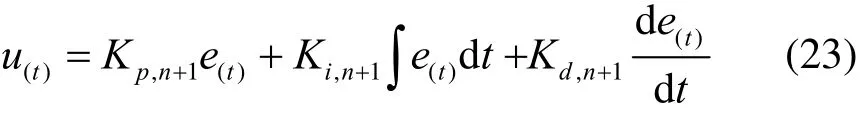
电压偏差E和偏差变化率EC的量化因子：Ke= 20，Kec=10，控制量Up、Ui、Ud的比例因子：Kup=5，Kui=10，Kud=1。

4 仿真分析

船用同步发电机的主要参数：P=1 875 kW，U=450 V，n=720 r/min，f=60 Hz，cosψ=0.8，Ra=0.009 8，船用同步发电机端电压变化仿真结果如图7和图8。

图7 采用可控相复励的仿真结果Fig. 7 Simulation result of controllable phase compound

图8 采用二维云模型PID的仿真结果Fig. 8 Simulation result of two dimensional cloud model PID

同步发电机空载启动后，在10 s时对两个励磁系统同时进行突加50%的负载，此时端电压下降，励磁系统为了维持端电压，励磁电压将会升高。从仿真结果曲线图7和图8分析计算后，得到了二维云模型PID励磁系统的超调量比可控相复励少了7.94%，调节时间缩短了0.36 s，最终稳态误差减小了0.51%。在20 s时同时对两个励磁系统进行突卸50%的负载后，此时端电压升高，为了响应端电压的变化，励磁系统的励磁电压将会降低，从而平衡同步发电机的端电压。二维云模型PID励磁系统的机端电压超调量比可控相复励少了6.88%，调节时间缩短了0.374 s，稳态误差减小了0.049%。

由于同步发电机运行时间过长，如温度升高，磨损等因素会导致同步发电机一系列参数值发生变化。

同步发电机参数发生变化后，再对可控相复励励磁系统和二维云模型PID励磁系统同时进行突加50%的负载试验和突卸50%的负载试验。

同步发电机参数发生变化后的仿真曲线如图9和图10。

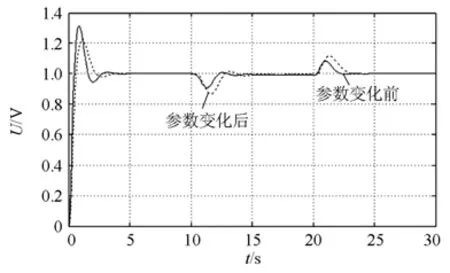
图9 参数值变化后采用可控相复励的仿真结果Fig. 9 Simulation result of controllable phase compound after parameter change

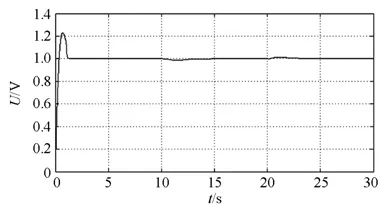
图10 参数值变化后采用二维云模型PID的仿真结果Fig. 10 Simulation result of two dimensional cloud model PID after parameter change

可控相复励励磁系统在参数变化后，在10 s时突加50%的负载和20 s时突卸50%的负载后，机端电压超调量明显增大，稳态误差也略有变化。二维云模型PID励磁系统在参数变化后进行10 s突加50%的负载和20 s时突卸50%的负载后，与参数变化前机端电压几乎没有上下波动，调节效果最佳，其超调量远小于可控相复励励磁系统，调节动作快，对时变性的电力系统参数具有很好的鲁棒性。

5 结论

二维云模型PID励磁控制器根据云规则模糊推理，自整定PID参数，并应用于船舶同步发电机励磁控制系统中。与传统相复励励磁系统对比仿真分析后，验证二维云模型PID励磁系统在船舶电力系统中具有更好的自适应性和鲁棒性，具有很好的应用价值。

[1] 曹帅, 张清枝. 同步发电机气隙对其稳定性和有功功率影响的研究[J]. 电力系统保护与控制, 2015, 43(15): 91-95. CAO Shuai, ZHANG Qingzhi. Research of influence of synchronous generator air-gap on stability and active power[J]. Power System Protection and Control, 2015, 43(15): 91-95.

[2] 沈浩然, 张建华, 丁磊, 等. 双馈异步发电机单相接地故障瞬态特性研究[J]. 电力系统保护与控制, 2015, 43(18): 6-11. SHEN Haoran, ZHANG Jianhua, DING Lei, et al. Transient characteristic research of doubly-fed induction generator during single-phase grounding fault[J]. Power System Protection and Control, 2015, 43(18): 6-11.

[3] 王涛, 张尚, 顾雪平, 等. 电力系统运行状态的趋势辨识[J]. 电工技术学报, 2015, 30(24): 172-179. WANG Tao, ZHANG Shang, GU Xueping, et al. Trends identification of power system operating states[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 172-179.

[4] 孙志凰, 刘辉, 汪旎. 同步发电机励磁与STATCOM非线性协调控制[J]. 电力系统保护与控制, 2014, 42(17): 8-13. SUN Zhihuang, LIU Hui, WANG Ni. Nonlinear coordinated control for synchronous generator excitation and STATCOM[J]. Power System Protection and Control, 2014, 42(17): 8-13.

[5] 雷邦军, 费树岷, 翟军勇, 等. 多机电力系统发电机自动电压调节器与SVC的协调控制[J]. 电工技术学报, 2015, 30(18): 131-139. LEI Bangjun, FEI Shumin, ZHAI Junyong, et al. Coordinated control of automatic voltage regulator and SVC in multi-machine power system[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 131-139.

[6] 年珩, 周义杰, 曾恒力. 开绕组永磁同步发电机的容错控制[J]. 电工技术学报, 2015 30(10): 58-66. NIAN Heng, ZHOU Yijie, ZENG Hengli. Fault-tolerant control technique of permanent magnet synchronousgenerator based on open winding configuration[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 58-66.

[7] SENJYU T, OMINE E, HAYASHI D, et al. Balancing control for dispersed generators considering torsional torque suppression and AVR performance for synchronous generators[J]. Electrical Engineering in Japan, 2010, 170(1): 16-25.

[8] 贺徽, 周建中, 谭建华, 等. 基于Mamdani模糊PID的同步发电机励磁控制[J]. 华中科技大学学报, 2010, 38(2): 34-37. HE Hui, ZHOU Jianzhong, TAN Jianhua, et al. Research and application of a fuzzy PID controller for excitation control systems in synchronous generators using mamdani model[J]. Journal of Huazhong University of Science & Technology, 2010, 38(2): 34-37.

[9] 揭海宝, 康积涛, 李平. 基于变论域模糊PID控制的同步发电机励磁研究[J]. 电力自动化设备, 2011, 31(6): 101-104. JIE Haibao, KANG Jitao, LI Ping. Research of a fuzzy PID excitation control systems in synchronous generators based on variable domain[J]. Electric Power Automation Equipment, 2011, 31(6): 101-104.

[10] 阎高伟, 龚杏雄, 续欣莹, 等. 基于云模型的球磨机料位概念表示与测量模型[J]. 中国电机工程学报, 2014, 34(14): 2281-2287. YAN Gaowei, GONG Xingxiong, XU Xinying, et al. Conceptual representation and measurement model of ball mill fill level based on cloud model[J]. Proceedings of the CSEE, 2014, 34(14): 2281-2287.

[11] 王迎超, 靖洪文, 张强, 等. 基于正态云模型的深埋地下工程岩爆烈度分级预测研究[J]. 岩土力学, 2015, 36(4): 1189-1194. WANG Yingchao, JING Hongwen, ZHANG Qiang, et al. A normal cloud model-based study of grading prediction of rockburst intensity in deep underground engineering[J]. Rock and Soil Mechanics, 2015, 36(4): 1189-1194.

[12] 李志民, 卢曦, 孙勇, 等. 同步发电机云模型励磁控制器的设计[J]. 电力系统及其自动化学报, 2010, 22(3): 91-95. LI Zhimin, LU Xi, SUN Yong, et al. Design of cloud model excitation controller for synchronous generator[J]. Proceedings of the CSU-EPSA, 2010, 22(3): 91-95.

[13] 孙才勤, 王贝贝, 张灵杰, 等. 船舶电力系统中同步发电机数学建模与仿真[J]. 大连海事大学学报, 2013, 39(1): 99-102. SUN Caiqin, WANG Beibei, ZHANG Lingjie, et al. Modeling and simulation for synchronous generator in marine power station system[J]. Journal of Dalian Maritime University, 2013, 39(1): 99-102.

[14] XU Z, ZHU P, MEI J. Research on backward cloud model with uncertainty[J]. Journal of Networks, 2013, 8(11): 2556-2563．

[15] AWADALLAH, MOHAMED A. Fuzzy-based on-line detection and prediction of switch faults in the brushless excitation system of synchronous generators[J]. Electric Power Components and Systems, 2010, 38(12): 1370-1388.

[16] LEON A E, SOLSONA J A, FIGUEROA J L, et al. Optimization with constraints for excitation control in synchronous generators[J]. Energy, 2011, 36(8): 5366-5373.

(编辑 葛艳娜)

Simulation research on PID excitation system of synchronous generator based on two-dimensional cloud model

LI Zongze, SHI Chengjun
(College of Marine Engineering, Dalian Marine University, Dalian 116026, China)

The cloud model is a powerful tool to achieve qualitative and quantitative uncertainty transforming. It integrates the fuzziness and randomness of objective things and solves the problem of nonlinear and uncertainties. For the nonlinearity, time-variability and uncertainty of excitation system in ship power system, the cloud model is applied to synchronous generator excitation control and two dimensional cloud model of PID excitation is designed. The forward cloud model is utilized to represent the voltage difference of synchronous generator and rate of voltage difference change concepts. Then the backward cloud generator is employed to generate the three parameters of PID concepts. Thus the cloud reasoning rule of double condition multi-rules of two dimensional cloud model is formulated and PID parameters of excitation controller are self-tuned. Through the establishment of models of synchronous generator controllable phase compound brushless excitation system and the two dimensional cloud model PID excitation system, the result of simulation shows that the two dimensional cloud model PID excitation controllable system model has better robustness and better adaptive ability.

synchronous generator; excitation; phase compound; two dimensional cloud model; control; simulation

10.7667/PSPC150930

2015-06-04；

2015-12-30

李宗泽(1989-)，男，通信作者，硕士研究生，研究方向为DMU轮机模拟器和海船船员智能评估系统；E-mail：554123749@qq.com

史成军(1963-)，男，副教授，研究方向为DMU轮机模拟器和海船船员智能评估系统。