抑制共振机理低频振荡的PSS设计方法

冯 双，蒋 平，吴 熙

(东南大学电气工程学院，江苏 南京 210096)

抑制共振机理低频振荡的PSS设计方法

冯 双，蒋 平，吴 熙

(东南大学电气工程学院，江苏 南京 210096)

电力系统稳定器(PSS)是抑制低频振荡最常用的方法，但安装了基于负阻尼机理设计的PSS后仍然可能发生共振机理低频振荡。推导了共振机理低频振荡幅值的数学表达式，并对振荡模式的共振特性进行分析。据此提出了抑制共振机理低频振荡的PSS设计方法。本方法设计的目标函数不仅考虑PSS的相位补偿特性，同时考虑了其幅频特性，能够更好地补偿振荡频率处所需相位并调整PSS提供的增益。此外根据不同振荡模式的共振特性计算得到不同的权重系数，保证了对系统危害更大的振荡模式能被更好地抑制。最后采用粒子群优化算法求得最佳的PSS参数。四机两区域系统中的仿真结果表明，相比传统的基于负阻尼机理设计的PSS，所提方法设计的PSS能够更加均衡有效地抑制共振机理低频振荡，同时不影响其原有的对负阻尼低频振荡的抑制效果。

共振机理低频振荡；电力系统稳定器；多模式振荡；参数设计

0 引言

随着电网规模的扩大，低频振荡发生的概率也大大增加，威胁了电网的安全稳定运行[1-2]。负阻尼机理是一种成熟的低频振荡机理[3]，但近年来国内外多次发生无法用负阻尼机理解释的低频振荡，比如在北美加拿大等系统都出现过不寻常的振荡过程，南方电网自2008年以来也发生过三次等幅低频振荡[4-5]。因此有学者提出了共振机理，该理论指出，当系统中的周期性功率扰动的频率接近系统低频振荡的固有频率时，会引起大幅度的功率振荡[6-7]。

现有的共振机理低频振荡的抑制方法包括提高电压、解列机组和将原动机切换为阀位控制[8-9]。这些方法需要在振荡发生一定时间后才能由控制人员执行操作，而共振机理低频振荡起振快速，因此若操作不及时可能导致事故范围扩大。此外由于实际系统中功率扰动源定位技术尚不十分成熟，及时准确地找到扰动源进行控制也存在一定难度，因此需要研究更加及时有效的抑制方法。电力系统稳定器(Power System Stabilizer, PSS)被广泛应用来抑制低频振荡，目前系统中安装的PSS大多是针对负阻尼低频振荡设计的[10]，但其对共振机理低频振荡的抑制效果不佳[5,8]。尤其随着越来越多具有不确定性和间歇性的新能源以及波动性负荷的接入，功率扰动源增多，并且成分复杂[11-12]，因此研究共振机理低频振荡的抑制具有实际意义。

本文推导了影响共振机理低频振荡幅值的因素，并分析了PSS抑制共振机理低频振荡的原理。在此基础上提出一种抑制共振机理低频振荡的PSS设计方法，考虑不同振荡模式的共振特性设计目标函数，并通过对权重系数的设计协调多振荡模式之间的抑制效果，然后采用粒子群算法进行优化求解，获得最佳的PSS参数。在四机两区域系统中的仿真结果证明本文所提出的设计方法可以更加均衡有效地抑制共振机理低频振荡。

1 共振机理低频振荡的特性

在典型的单机无穷大系统中，发电机采用二阶模型，发电机转子角Δδ的线性化状态方程为

其中：M为发电机惯性时间常数；D为发电机阻尼转矩系数；K为发电机同步转矩系数；ΔPm为功率扰动，可以为机械功率扰动、负荷扰动等常见扰动。

一般假设ΔPm为正弦信号扰动，其形式为

其中：r为扰动幅值；ω为扰动角频率。将式(2)代入式(1)，并求解可得Δδ在稳态的幅值如式(3)所示[6-7]。

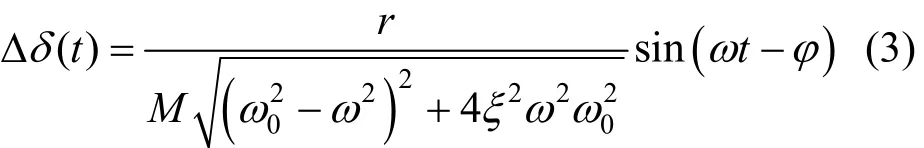
其中：ω0为系统自然振荡角频率；ξ为阻尼比。

由(3)可知，Δδ的幅值大小与ω相关，ω可表示为ω=f·(2π)，f为功率扰动频率。当f等于共振频率fr时，Δδ的幅值达到最大值，此时即发生了共振机理低频振荡。共振频率fr的表达式为

在系统弱阻尼的情况下，ξ<1，共振频率fr约等于系统自然振荡频率f0，即fr=f0=ω0/(2π)。当扰动频率接近系统共振频率时，就会引发共振机理低频振荡，振荡幅值为

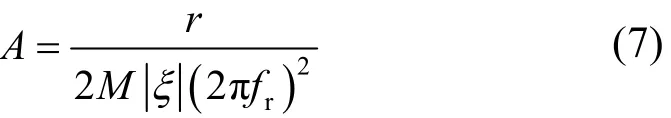
由式(7)可得，振荡幅值A与扰动幅值r、阻尼比ξ以及共振频率fr相关，结合图1和式(7)可以看出振荡幅值A与扰动幅值r成正比，与阻尼比ξ以及共振频率fr的平方成反比。

图1 r-A，ξ-A和-A线图Fig. 1 Curves of r-A,ξ-A and

2 PSS抑制共振机理低频振荡的原理

目前系统中最常见的抑制低频振荡装置为PSS，它可以有效抑制负阻尼低频振荡，根据本文分析，在设计合理的情况下也可以较好地抑制共振机理低频振荡。

2.1 PSS结构

图2为PSS结构图，其中u为输入信号，可以为发电机转速、功率信号等。u经过增益环节、隔直环节、超前滞后环节形成输出信号UPSS，UPSS和电压偏差信号Ut-Uref共同经过励磁系统调节得到励磁参考电压Eref。图2中Kw为PSS增益，Tw为隔直环节时间常数，T1、T2为超前滞后环节时间常数。

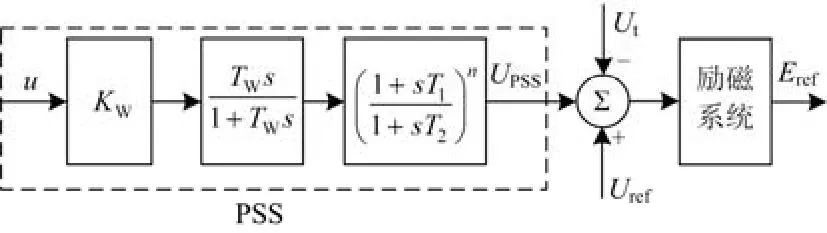
图2 PSS结构图Fig. 2 Structure of PSS

2.2 PSS抑制共振机理低频振荡原理

PSS抑制共振机理低频振荡的原理如图3所示。其中-ΔPe和ΔUPSS分别为PSS的输入信号和输出信号，ΔPe为发电机输出有功功率，θEX表示在振荡频率处励磁系统的滞后角，θPSS为PSS在振荡频率处提供的角度，ΔTPSS为PSS引入的附加转矩。

图3 PSS抑制共振机理低频振荡原理图Fig. 3 Principle diagram of PSS for suppressing LFO of resonance mechanism

由于ΔTPSS与Δω相位相同，PSS增加了系统阻尼转矩Td，又ΔTd和阻尼比ξ的关系为

因此Td的增加等同于阻尼比ξ的增加，根据式(7)，振荡幅值A反比于阻尼比ξ，因此阻尼比ξ增加时，振荡幅值A减小，则共振机理低频振荡得到了抑制。

2.3 相位补偿法的设计原则

PSS的设计关键在于超前滞后环节的参数选择，最常用的设计方法为相位补偿法[13]。超前滞后环节的传递函数为

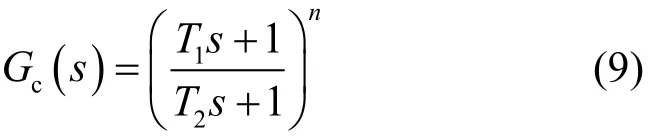
其中：s为拉普拉斯算子；T1、T2为超前滞后环节的时间常数；n为超前滞后环节的个数。式(9)的中心频率fc为

相位补偿的设计目标为附加转矩ΔTPSS应尽量靠近Δω轴，根据图4可得。当输入信号为-ΔPe时，需要补偿的相位为

PSS实际提供相位应尽量等于需要补偿的相位以保证PSS获得合适的相频特性，使其提供的附加阻尼转矩为正。此外超前滞后环节的中心频率fc应尽量接近共振频率fr，以保证PSS获得合适的幅频特性。

对于单模式振荡，PSS可以在振荡频率处提供所需的相位，并且保证超前滞后环节的中心频率fc等于共振频率fr。但是对于多模式振荡，PSS不一定能在每个振荡频率处都提供所需的相位，因此需要根据各模式的共振振荡特性来进行相位补偿并且调整中心频率大小，从而获得更好的抑制效果。

3 考虑共振特性的PSS设计方法

对于负阻尼低频振荡，阻尼比越大，对应振荡模式的幅值衰减越快。但是对于共振机理低频振荡，其振荡幅值不仅仅和阻尼比有关。因此传统的针对负阻尼低频振荡的设计方法直接用于设计抑制共振机理低频振荡的PSS会导致抑制效果不佳。本节提出了一种针对共振机理低频振荡的PSS设计方法。

3.1 目标函数

根据第2.3节的相位补偿法设计原则，目标函数J为

式中：f1，f2，…，fn为n个振荡频率；αi为第i个振荡模式的加权因子；θd(fi)为振荡频率fi处PSS产生的附加阻尼转矩与Δω轴之间的夹角，该项为保证PSS实际补偿的相位与需要补偿的相位差尽量小；θcend(fi)为相位补偿环节中心频率处补偿的相角与振荡频率fi处待补偿的相角之差，该项为保证PSS的中心频率尽量靠近振荡频率。当所需抑制的振荡模式较多时，可采用多通道PSS[10]，每个通道抑制2-3个频率的振荡模式，其中每个通道超前滞后环节的参数都按照式(12)进行设计。

传统的设计方法只包含式(12)的第一项，并且加权因子αi均为1，来使得PSS获得期望的相频特性，然后通过增大增益Kw来同时增加各模式的阻尼。而式(12)一方面可以通过改变加权因子来调整各振荡模式相位被补偿的程度，另一方面可以调整各振荡模式的增益，越靠近中心频率的振荡模式在相同的PSS的增益的情况下的总体增益更大，因此加权因子更大的振荡模式可以被更好地抑制。

3.2 加权因子

对于共振机理低频振荡，权重因子的设置必须考虑不同振荡模式的共振特性。由式(7)可知共振机理低频振荡稳态时的振荡幅值与扰动幅值r成正比，与发电机惯性时间常数M、阻尼比ξ、频率fr的平方成反比。对于一台特定的发电机，M为常数，但不同振荡模式的阻尼比ξ和振荡频率fr不同，在扰动幅值相同的情况下，振荡频率fr越低，阻尼比ξ越小引起的共振幅值更大。因此在设计针对共振机理低频振荡的PSS时，应着重考虑此类振荡模式，它们对电网稳定性的危害更大。本文根据不同共振振荡模式的特性分配不同加权因子，使得对电网稳定性危害更大的振荡模式能更好地满足相位补偿环节的设计原则，因此定义加权因子的表达式为

式中：ξset为期望阻尼比，至少设置为0.05；ξi为该振荡模式的阻尼比。它保证了阻尼比越小，频率越低的振荡模式能够更好地满足相位补偿的设计原则。

3.3 优化方法

由于与其他优化算法相比，粒子群算法(Particle Swarm Optimization，PSO)算法具有无需采用二进制编码、数学逻辑基础简单、目标函数容易实现以及对优化目标灵敏性较高等优势[14-15]。本文以式(12)为优化数学模型，采用PSO算法进行优化，求得满足目标函数的最佳参数组。

4 仿真验证

本节在典型的四机两区系统进行了仿真研究，验证所提方法的有效性，系统结构图如图4所示[16]。

图4 四机两区系统机构图Fig. 4 Structure of four-machine and two-area system

4.1 PSS设计过程

对系统进行模态分析可知系统中存在表1所示的三种振荡模式。其中模式2、3与发电机G4相关，且模式3的振荡频率和阻尼比更低，需要重点考虑。

表1 四机两区系统模态分析表Table 1 Modal analysis results of the system

由于相同频率和幅值的机械功率扰动和负荷功率扰动，前者引发的共振机理低频振荡的幅值更大，对系统的危害也更大[17]，因此本文以机械功率扰动为例进行仿真。设发电机G4的机械功率出现周期性扰动，则振荡发散，因此需要在G4上配置PSS。分别根据传统设计方法和本文方法得到表2中的参数组1和参数组2。

表2 PSS参数Table 2 Parameters of PSS

4.2 仿真结果和分析

在发电机G4的输出机械功率上添加扰动幅值为0.05 p.u.，频率1.16 Hz的扰动，扰动时间为2～20 s，激发模式2的共振振荡，在20 s之后扰动被切除。分别采用参数组1和2时，发电机G4的输出有功功率如图5所示。采用参数组2的振荡幅值比采用参数组1的振荡幅值小15.11%。

图5 振荡模式2下G4的输出有功功率Fig. 5 Output active power of G4 of mode 2

在发电机G4的输出机械功率上添加频率为0.64 Hz的扰动，其他参数同上，则激发了模式3的振荡，分别采用两组参数时的发电机G4的输出有功功率如图6所示。采用参数组1时，模式2的振荡幅值为1.4×10-2，而模式3的振荡幅值为2.8×10-2，为模式2的2倍。说明传统方法设计的PSS对具有更低频率和阻尼比的振荡模式的抑制效果不佳，与3.2节的理论分析一致。而采用了参数组2后，模式3的振荡幅值减小了39.93%。

图6 振荡模式3下G4的输出有功功率Fig. 6 Output active power of G4 of mode 3

从模式3和模式2相对振幅的角度对两种设计方法进行比较，图7和图8分别为采用参数组1和参数组2时G4的输出有功功率。采用参数组1时，A3/A2为2，其中A2、A3分别表示模式2和模式3的振幅，这说明模式2的抑制效果要优于模式3。

图7 参数组1下G4的输出有功功率Fig. 7 Output active power of G4 with parameter set 1

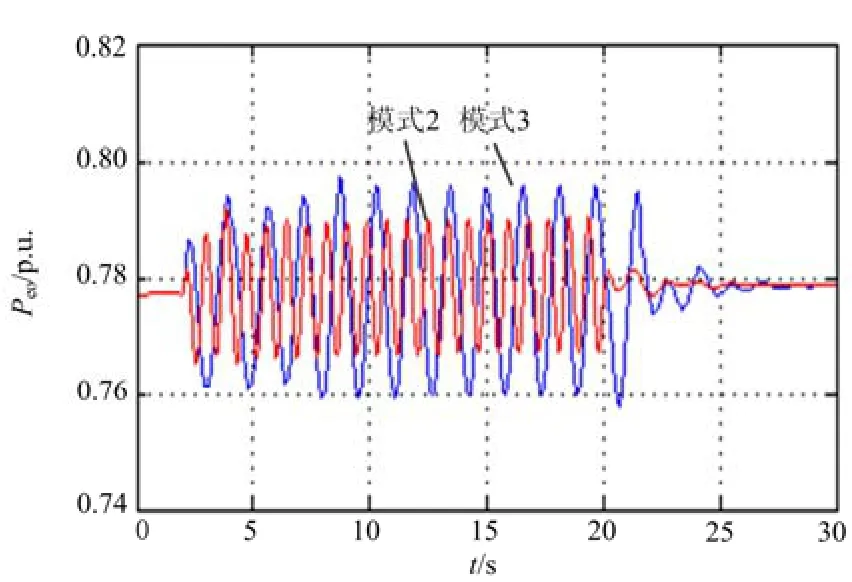
图8 参数组2下G4的输出有功功率Fig. 8 Output active power of G4 with parameter set 2

当采用参数组2时，A3/A2的值为1.4，减小了30%，说明所提方法能够更好地协调不同振荡模式之间的抑制效果，克服传统方法对振荡频率较低和阻尼较弱的共振振荡模式抑制效果不佳的缺点。

表3比较了传统方法和本文所提方法的抑制效果，可见采用所提方法设计的PSS不仅能够减小两种共振振荡模式各自的振幅，也能减小两种模式的相对振幅，避免PSS对不同振荡模式抑制效果不均衡的情况。

表3 传统设计方法和本文设计方法抑制效果比较Table 3 Comparison between traditional and proposed method

由于PSS的一个重要功能是抑制负阻尼低频振荡，因此下面对使用所提出方法设计的PSS对负阻尼低频振荡的抑制效果进行验证。在区域间联络线上靠近区域2一端的母线上设置三相接地短路，开始时间为5 s，持续时间0.1 s，图9为分别采用参数组1和参数组2时G4的输出有功功率。从图9可以看出，PSS采用本文提出的设计方法得到的参数组2时不影响其原有的抑制负阻尼低频振荡的性能。

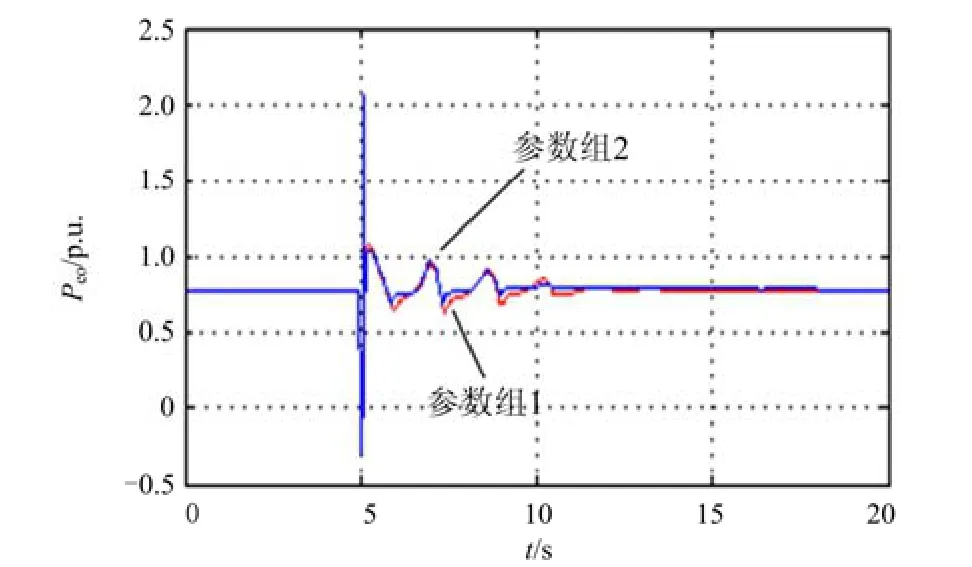
图9 负阻尼低频振荡时G4的输出有功功率Fig. 9 Output active power of G4 under LFO of negative damping mechanism

5 结论

本文提出了一种抑制共振机理低频振荡的PSS设计方法。本方法的目标函数不仅考虑了相位补偿特性，还考虑了幅频特性，同时根据不同振荡模式的共振特性设置不同的权重因子。最后通过PSO算法进行优化求解。本方法的目标函数保证了对系统危害更大的振荡模式所需相位能够被更好地补偿，并且获得更大的增益。四机两区域系统中的仿真表明，相比于传统的针对负阻尼低频振荡的PSS设计方法，本方法设计的PSS能够更加有效地减小共振振荡的幅值，同时还能均衡协调多种模式共振机理低频振荡的抑制效果，避免频率更低、阻尼更弱的振荡模式对系统稳定造成更大的危害，并且不影响PSS原有的抑制负阻尼低频振荡的性能。

[1] 孙建波, 赵娴, 李大虎, 等. 利用储能抑制互联电力系统联络线功率振荡的研究[J]. 电力系统保护与控制, 2013, 41(17): 10-17. SUN Jianbo, ZHAO Xian, LI Dahu, et al. Study on energy storage in damping tie line power oscillations in power system[J]. Power System Protection and Control, 2013, 41(17): 10-17.

[2] 屈博. 基于 WAMS 的电力系统低频振荡在线辨识与抑制[D]. 北京: 北京交通大学, 2014. QU Bo. Online identification and suppression of low frequency oscillation in power system based on WAMS[D]. Beijing: Beijing Jiaotong University, 2014.

[3] BEZA M, BONGIORNO M. An adaptive power oscillation damping controller by STATCOM with energy storage[J]. IEEE Transactions on Power Systems, 2014, 30(1): 484-493.

[4] 肖鸣, 梁志飞. 南方电网强迫功率振荡事故分析及其处置措施[J]. 南方电网技术, 2012, 6(2): 51-55. XIAO Ming, LIANG Zhifei. Analysis on the forced oscillation failure in china southern power grid and its handling measures[J]. Southern Power System Technology, 2012, 6(2): 51-55.

[5] 耿天翔, 张竹竞, 项丽, 等. 基于起振特性的强迫振荡扰动源定位及解列方案[J]. 电力系统保护与控制, 2015, 43(6): 98-103. GENG Tianxiang, ZHANG Zhujing, XIANG Li, et al. A locating and splitting scheme for disturbance source of forced power oscillation based on the propagation characteristic[J]. Power System Protection and Control, 2015, 43(6): 98-103.

[6] 马燕峰, 赵培龙, 赵书强. 多机电力系统的强迫功率振荡特性研究[J]. 电力系统保护与控制, 2013, 41(24): 23-29. MA Yanfeng, ZHAO Peilong, ZHAO Shuqiang. Research on characteristics of forced power oscillation in multi-machine power system[J]. Power System Protection and Control, 2013, 41(24): 23-29.

[7] 贾勇, 何正友. 基于受扰轨迹的低频振荡分析方法综述[J]. 电力系统保护与控制, 2012, 40(11): 140-148. JIA Yong, HE Zhengyou. Review on analysis methods for low frequency oscillations based on disturbed trajectories[J]. Power System Protection and Control, 2012, 40(11): 140-148.

[8] 文贤馗, 钟晶亮, 钱进. 电网低频振荡时汽轮机控制策略研究[J]. 中国电机工程学报, 2009, 29(26): 107-111. WEN Xiankui, ZHONG Jingliang, QIAN Jin. Research on the control strategy for turbine on low-frequency oscillation[J]. Proceedings of the CSEE, 2009, 29(26): 107-111.

[9] 刘辉, 杨寅平, 田云峰, 等. 电力系统强迫功率振荡实例及机理分析[J]. 电力系统自动化, 2012, 36(10): 113-117. LIU Hui, YANG Yinping, TIAN Yunfeng, et al. Instances and mechanism analysis of forced power oscillation in power system[J]. Automation of Electric Power Systems, 2012, 36(10): 113-117.

[10] 马曦, 何旭, 杜冰心. 电力系统稳定器 PSS4B 的仿真研究[J]. 电网与清洁能源, 2014, 30(2): 33-37. MA Xi, HE Xu, DU Bingxin. Simulation research of power system stabilizer PSS4B[J]. Power System and Clean Energy, 2014, 30(2): 33-37.

[11] 谭谨, 王晓茹, 李龙源. 含大规模风电的电力系统小扰动稳定研究综述[J]. 电力系统保护与控制, 2014, 42(3): 15-23. TAN Jin, WANG Xiaoru, LI Longyuan. A survey on small signal stability analysis of power systems with wind power integration[J]. Power System Protection and Control, 2014, 42(3): 15-23.

[12] 史华勃, 刘天琪, 李兴源. 交直流输电系统低频振荡仿真分析[J]. 电力系统及其自动化学报, 2013, 25(1): 47-52. SHI Huabo, LIU Tianqi, LI Xingyuan. Simulation analysis on low frequency oscillation in the AC/DC transmission system[J]. Proceedings of the CSU-EPSA, 2013, 25(1): 47-52.

[13] DU W, WANG H F, CAO J, et al. Application of the phase compensation method for the design of a DC/AC converter-based stabilizer to damp inter-area power oscillations[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1302-1310.

[14] 刘蔚, 赵勇, 吴琛, 等. 一种提高多小水电群送出能力的PSS参数协调优化方法[J]. 电力系统保护与控制, 2015, 43(4): 44-50. LIU Wei, ZHAO Yong, WU Chen, et al. A method of PSS parameters coordinated optimization for the improvement of transmission capacities of multiple small hydropower station groups[J]. Power System Protection and Control, 2015, 43(4): 44-50.

[15] LI C, YANG S. A self-learning particle swarm optimizer for global optimization problems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B, Cybernetics, 2012, 42(3): 627-646.

[16] KUNDUR P. Power system stability and control[M]. New York: McGraw-Hill Inc., 1993: 813-814, 817-818.

[17] 韩志勇, 贺仁睦, 马进, 等. 电力系统强迫功率振荡扰动源的对比分析[J]. 电力系统自动化, 2009, 33(3): 16-19. HAN Zhiyong, HE Renmu, MA Jin, et al. Comparative analysis of disturbance source inducing power system forced power oscillation[J]. Automation of Electric Power Systems, 2009, 33(3): 16-19.

PSS design method for suppressing low-frequency oscillation of resonance mechanism

FENG Shuang, JIANG Ping, WU Xi
(School of Electrical Engineering, Southeast University, Nanjing 210096, China)

Low-frequency oscillation (LFO) of resonance mechanism could still happen after installing PSS which is the most common method of suppressing LFO. This paper deduces the mathematical expression of the amplitude of LFO of resonance mechanism and analyzes the influencing factors. Then, a design method of PSS for suppressing LFO of resonance mechanism is proposed. In this method, the object function is designed considering both the phase and amplitude frequency characteristic to provide better compensation angle and adjust the gain PSS provides. Besides, weight factors are obtained according to the resonance characteristics of each mode, so that the oscillation mode which causes more damage to the power grid can be better suppressed. Particle swarm optimization is used to search the optimal solution. The simulation results in four-machine and two-area system demonstrate that, compared with PSS designed according to negative damping mechanism, PSS designed by the proposed method has better damping effect on LFO of resonance mechanism without affecting the suppression effect of LFO of negative damping mechanism.

This work is supported by National Natural Science Foundation of China (No. 51577032) and Natural Science Foundation of Jiangsu Province (No. BK20140633).

low-frequency oscillation of resonance mechanism; power system stabilizer; multimode oscillation; parameter design

10.7667/PSPC151028

2015-06-18；

2015-08-18

冯 双(1990 -)，女，博士研究生，研究方向为电力系统稳定运行与控制；E-mail: fengshuang429@139.com

(编辑 葛艳娜)

国家自然科学基金面上项目(51577032)；江苏省自然科学基金(BK20140633)

蒋 平(1954 -)，男，博士，教授，博士生导师，从事电力系统运行与控制和电力电子在电力系统中的应用方面的研究工作。