计及风力发电风险的电力系统多目标动态优化调度

杨家然，王兴成，蒋 程，罗晓芬

(1.大连海事大学, 辽宁 大连 116026；2.国网北京市电力公司，北京 100031；3.华能威海发电有限责任公司，山东 威海 264205)

计及风力发电风险的电力系统多目标动态优化调度

杨家然1，王兴成1，蒋 程2，罗晓芬3

(1.大连海事大学, 辽宁 大连 116026；2.国网北京市电力公司，北京 100031；3.华能威海发电有限责任公司，山东 威海 264205)

为解决风电的随机性给电力系统调度带来的问题，引入负荷预测误差和风速的概率分布函数来建立负荷及风电功率的随机性模型。基于对负荷及风电功率随机性模型的深入分析，对风电接入将导致系统维持稳定运行的成本增加风险加以考虑。并在约束条件中引入失负荷及风电浪费风险指标，构建计及风力发电风险的电力系统多目标优化调度模型，以实现系统总污染排放量最少和运行成本最低的综合优化目标。采用一种新颖的蝙蝠算法对模型进行求解，并对蝙蝠算法的不足之处进行了改进，有效地解决了该算法迭代后期收敛慢、易陷入局部极值等问题。以含大规模风电并网电力系统为例进行环境经济调度仿真，验证了所提模型及算法的有效性，并进一步分析了相关参数对含风电并网电力系统优化调度的影响。

风电；电力系统；环境经济调度；多目标优化；蝙蝠算法

0 引言

为应对全球能源危机和环境恶化，风力发电技术发展迅速，并网风电场规模日益扩大。由于风电功率具有强烈的间歇性和随机波动性特点，当风电渗透率达到一定比例，在提高经济效益和改善环境的同时也给电力系统运行增加了风险[1-2]。

为减小风电并网带来的风险，构建优化调度模型必须对风电功率的随机性加以考虑。目前主要的处理方法包括风速预测、模糊建模和概率分析等[3]。概率分析法首先对大量风速样本进行统计分析得到风速概率分布模型，进而通过风速—风电功率关系转换为风电出力概率分布模型，相对而言更具客观性和可行性。研究表明，双参数威布尔(Weibull)分布曲线能较好地拟合实际风速概率分布函数[4]。

本文引入负荷预测误差和风速的概率分布函数来建立负荷及风电功率的随机性模型。对风电接入将导致系统维持稳定运行的成本增加风险加以考虑，并在约束条件中引入失负荷及风电浪费风险指标，构建计及风力发电风险的电力系统多目标优化调度模型，采用改进蝙蝠算法对模型进行求解。最后以含大规模风电并网系统为例进行仿真，验证了所提模型及算法的有效性，并进一步分析了相关参数对含风电并网电力系统优化调度的影响。

1 随机性模型分析

1.1 负荷的随机性模型

在进行系统负荷预测时，常采用正态分布来描述负荷预测误差。负荷预测误差的概率密度函数为

1.2 风电功率的随机性模型

为简化表达风电功率与风速的关系，本文采用线性分段函数如式(2)所示[5]。

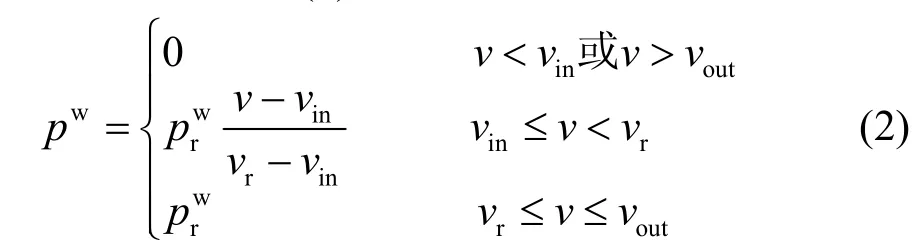
式中：vr、vin、vout分别为风力机的额定风速、切入风速、切出风速；为风力机的额定功率。

为简化模型，假设风电场中每台风力机是完全一样的，同时忽略尾流效应，总风电功率可表示为

式中：wp为一台风力机的功率；windP为风电场中实际可用总风电功率；wN为风力机个数。风电场额定功率可表示为

对大量实测风速的统计结果表明，区域风速变化规律服从两参数的威布尔分布[6]，以随机变量V表示风速，则其概率密度函数及分布函数表达式为

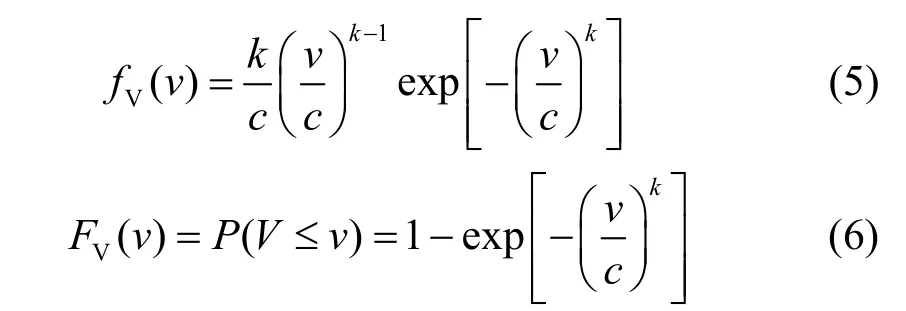
式中，k和c分别为威布尔分布的形状参数和尺度参数。

综合式(2)、式(3)、式(5)、式(6)可知，风电场的总输出功率windP为混合型的随机变量，根据概率论相关理论，可以求得风电场总功率的概率分布特性。风电场总功率离散部分的分布率可表示为

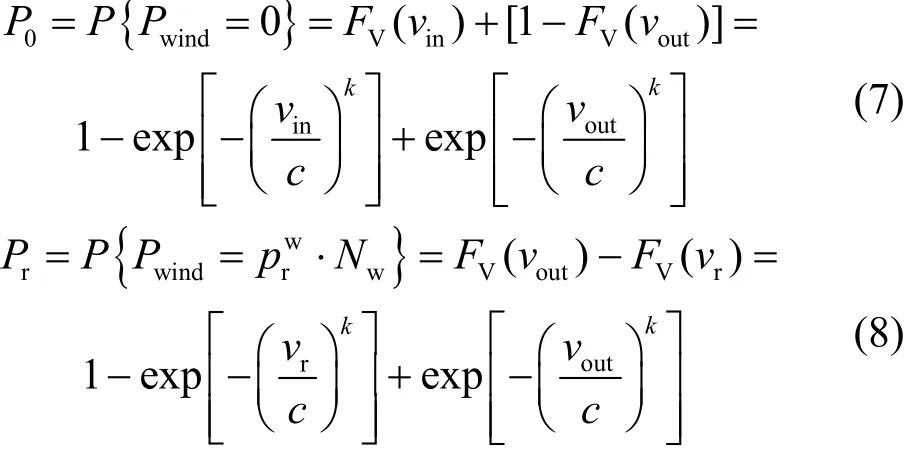
风电总功率连续部分的概率密度函数为

2 考虑随机性因素的风险模型

2.1 失负荷风险指标

本文采用文献[7]提出的方法来确定系统风险指标。系统失负荷风险指标定义为：系统正旋转备用量小于系统负荷随机波动量的概率，是由风电计划出力大于实际风电功率、负荷被低估、常规机组强迫停运等因素导致。本文仅考虑没有常规机组停运及仅一台常规机组强迫停运的情况。

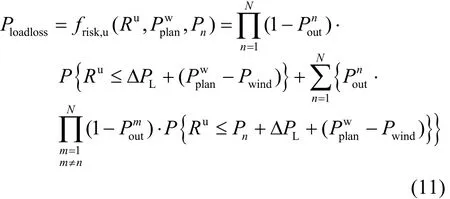
2.2 风电功率浪费风险指标

风电功率浪费风险指标定义为：系统负旋转备用量小于系统负荷随机波动量的概率，是由实际可利用风电功率超过调度计划值导致。

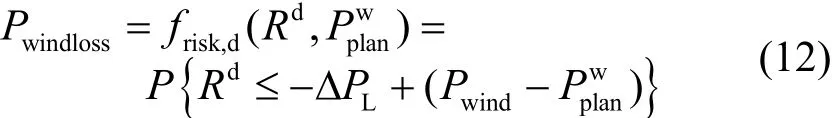
式中，Rd为系统负旋转备用量。

3 含风电系统多目标优化调度模型

3.1 环境污染目标函数

常规机组发电需要消耗大量化石类能源，并向大气中排放气体污染物。本文在此采用污染气体综合排放模型[8]。若系统共有n台常规机组，则调度时段内系统污染气体排放总量E可表示为

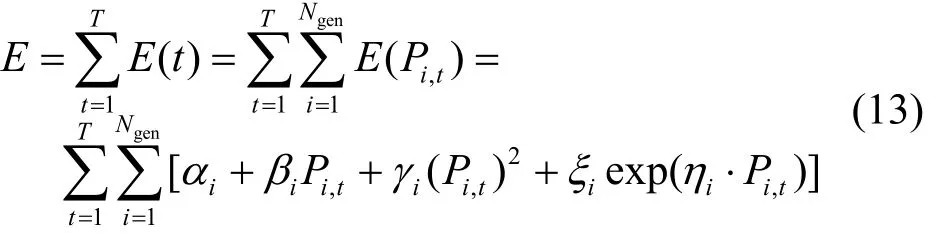
式中：Pi,t为常规机组i第t时段的出力；E为整个调度时段T的废气排放；E(t)为第t时段的废气排放，单位为t/h；Ngen为常规机组数；E(Pi,t)为常规机组i在第t时段的废气排放函数；ia、ib、ig、ix和ih为给定污染气体排放系数。

3.2 经济性目标函数

3.2.1 常规电能费用

计及阀点效应的常规机组燃料成本表示为[9]

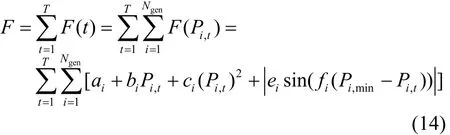
式中：F为整个时段T的燃料成本；F(t)为第t时段的燃料成本；F(Pi,t)为常规机组i在第t时段的燃料成本函数；ai、bi和ci为给定成本系数；ei、fi为阀点效应相关系数。

3.2.2 风电费用

风电费用包括：风电价格成本CW、风电功率低估代价CLow、风电功率高估代价CHigh[10]。风电并网要支付的费用可看作风电价格成本，设其与风电功率调度计划值成正比，则可表示为

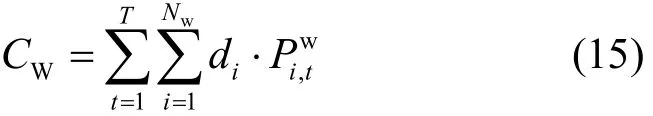
式中：di为第i台风电机组的价格成本系数；第i台风电机组第t时段的调度计划值。

风电低估代价LowC定义：风电功率实际值被低估，由此增加的系统平衡调整费用或能源浪费惩罚费用。

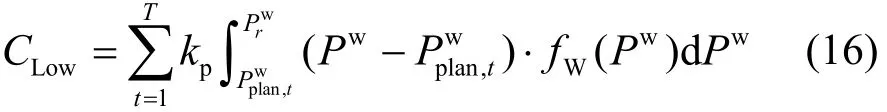
风电高估代价HighC定义：风电功率实际值被高估，由此增加的系统旋转备用及平衡调整费用。

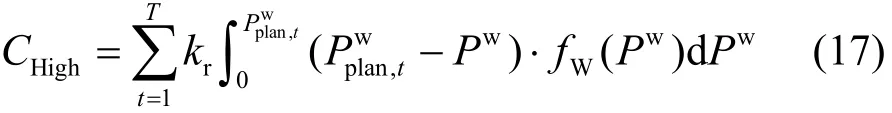
式中，rk为风电功率高估代价系数。

3.3 约束条件

假设风电场中各风电机组出力相同，第t时段风电场总计划出力则可表示为调度模型约束条件如下：

1) 各时段有功功率平衡方程为

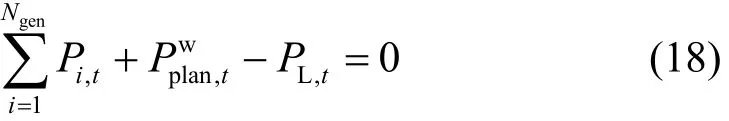
式中，L,tP为第t时段负荷预测值。

2) 各时段常规机组出力上下限约束为

3) 各时段风电场计划出力约束为

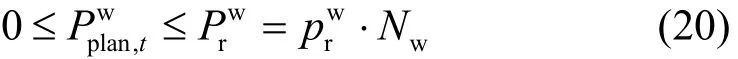
4) 常规机组爬坡率约束为

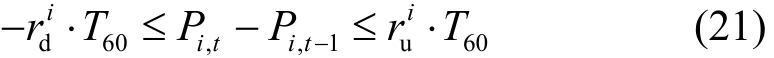
5) 基于正旋转备用的风险约束

为保证系统可靠性，系统失负荷风险指标不能超过给定的风险槛值[11]。

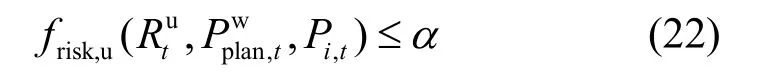
式中，a为失负荷风险槛值。

系统正旋转备用量不能大于系统正常运行状态及1N-状态下可提供的最大正旋转备用量，即

系统1N-状态下提供总的正旋转备用容量为

6) 基于负旋转备用的风险约束

为避免风能的浪费，同样需要将风电功率浪费风险指标约束在要求的范围之内，即满足如下约束：

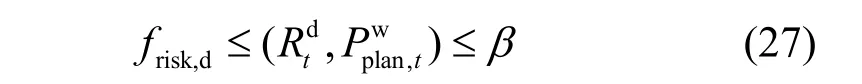
式中，b为风电功率浪费的风险槛值。

系统负旋转备用量不能大于系统正常运行状态及1N-状态下所能提供的最大负备用量[11]。

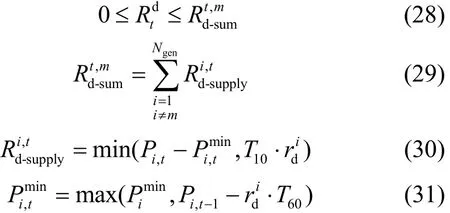
综上可得优化调度模型为

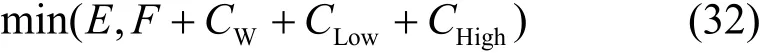
约束条件对应式(18)～式(22)、式(27)。

4 模型的求解

4.1 基本蝙蝠算法

蝙蝠算法(Bat Algorithm, BA)由Xin-She Yang提出，能够搜索全局最优解，但蝙蝠算法也存在迭代后期收敛慢、易陷入局部极值等问题[12]。基本蝙蝠算法流程参考文献[12]。

4.2 改进蝙蝠算法

本文引入惯性权重系数w对BA加以改进，即改进蝙蝠算法(Improved Bat Algorithm, IBA)。当w较大时，蝙蝠能够扩展搜索空间，搜索新的区域，提高BA算法的全局搜索能力。当w较小时，蝙蝠在当前解领域搜索，局部搜索能力增强，收敛速度加快。惯性权重系数w、蝙蝠速度按式(33)、式(34)更新。

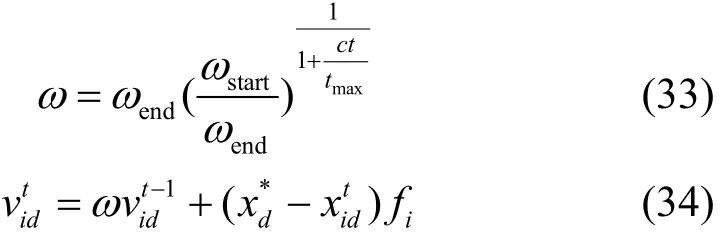
式中：wstart为惯性系数的起始值；wend为惯性系数的终止值；t为当前迭代次数；c为惯性权重相关系数；tmax为最大迭代次数。

基于IBA算法的计及风力发电风险的电力系统多目标优化调度流程图如图1所示。

5 算例分析

将本文所提调度模型在具有一个并网风电场的10机组系统中进行仿真计算。该风电场共有100台额定功率为1.5 MW的风力发电机。风电场风速参数如下：该地区风速所服从的威布尔分布形状参数k和尺度参数c分别为2.1和8.8；风电价格成本系数d为10 $/(MW·h)，风电低估和高估代价系数(kp和kr)均为18 $/(MW·h)。本文设定系统研究周期为3 h，每个时段为1 h，3个时段风速预测值分别为：10.2 m/s、12.6 m/s、16.1 m/s。

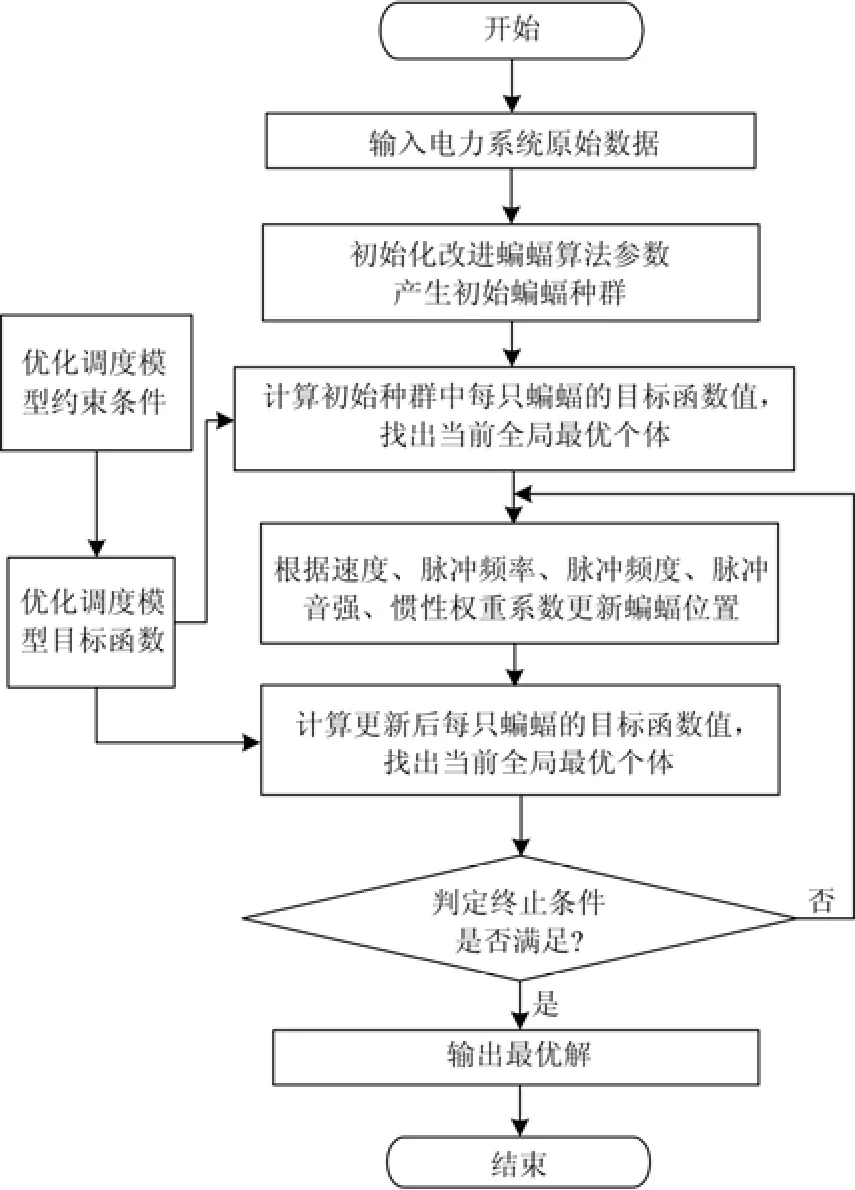
图 1 基于改进蝙蝠算法的流程图Fig. 1 Flow chart of modified bat algorithm

表1所示为常规机组爬坡率及强迫停运概率。各常规机组的其他参数见文献[13-14]。假设各调度时段负荷不变，负荷预测值和预测误差的标准差分别为2 360 MW和50 MW。

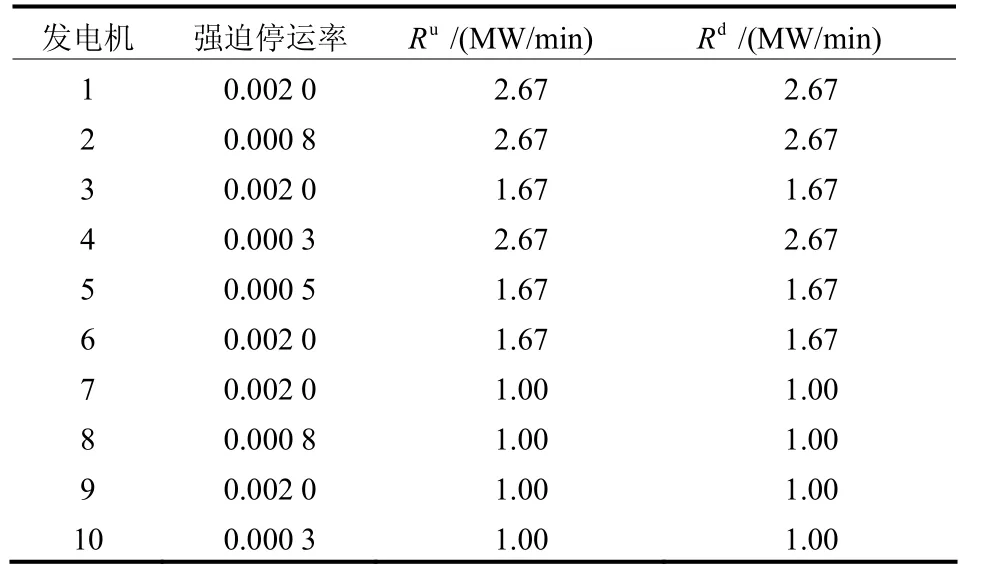
表1 常规机组强迫停运概率及爬坡率Table 1 Forced outage probability and ramp rate of conventional generator

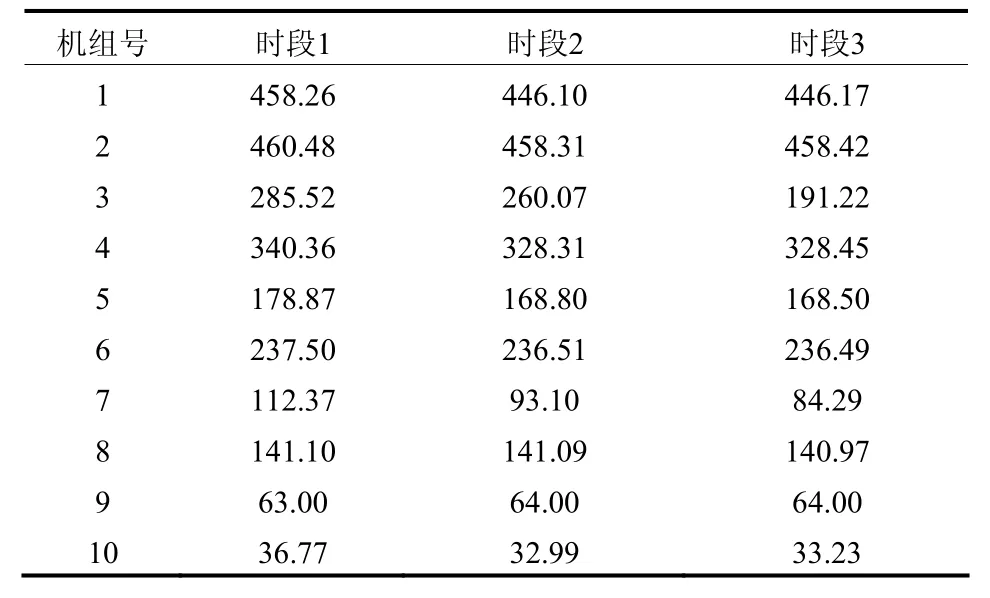
表2 常规机组输出的有功功率Table 2 Scheduled power outputs of conventional generator MW

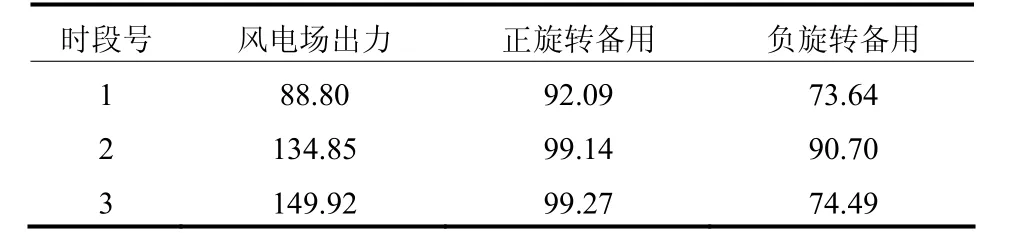
表3 风电场计划出力及系统正、负旋转备用需求Table 3 Scheduled power outputs of wind farm up and down spinning reserve demand MW

表4 常规机组各时段废气排放量Table 4 Exhaust emissions of conventional generator per hour

图2为总发电成本关于系统风险槛值a的函数曲线。由图2可以看出，总发电成本随着a的增加而减小。说明系统对风险约束要求的降低有利于经济性的提升。

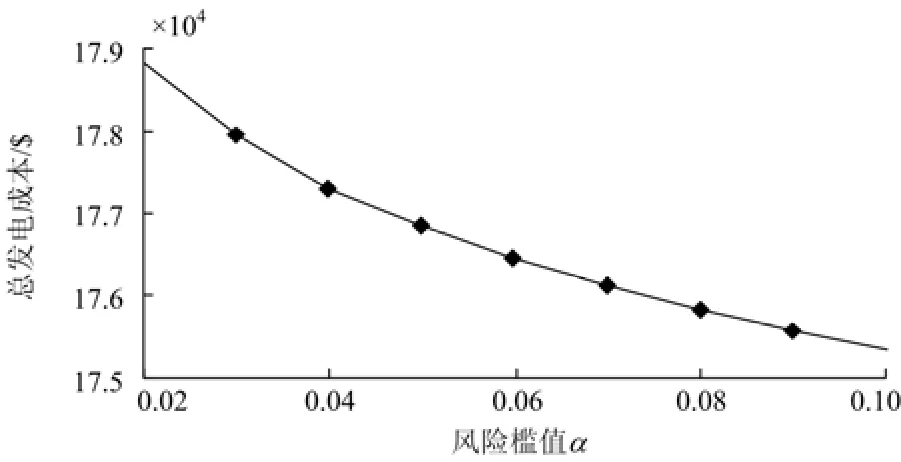
图2 总发电成本关于风险槛值α的函数曲线Fig. 2 Total generation cost as a function ofαa

根据图3、图4所示曲线来分析不同rk对三时段调度结果的影响。此时，保持风险槛值a、b为0.05。当rk小于20 $/(MW•h)时，发电总成本会随着rk的增加而不断增加。超过20 $/(MW•h)以后，发电总成本则几乎不变。这一结果可以通过图4来解释。在满足系统风险约束的前提下，为了防止不断增长的rk导致HighC的大幅度增加，必须限制风电功率调度计划值。当rk增大到一定程度的时候，风电场的计划出力不再降低，几乎保持恒定的数值，发电总成本也相应保持恒定。

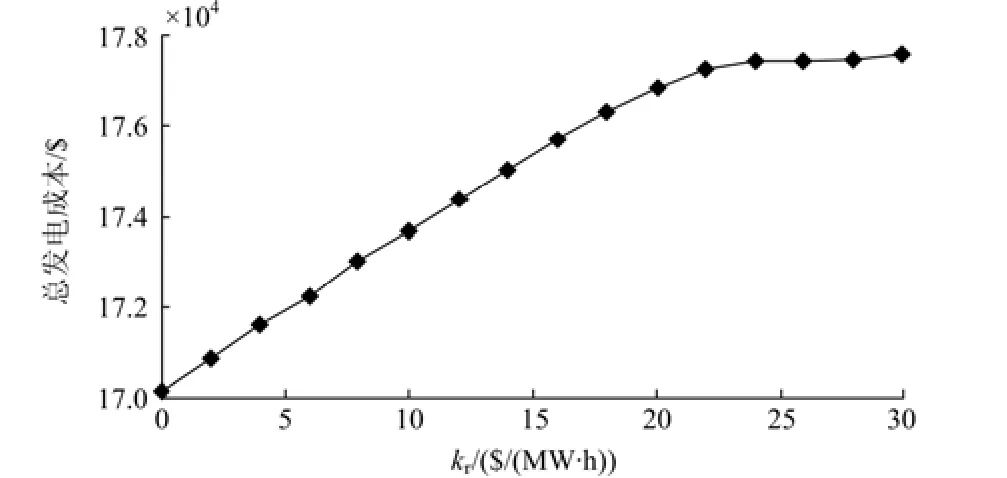
图3 总发电成本关于高估代价系数函数曲线Fig. 3 Total generation cost as a function of up reserve cost coefficient

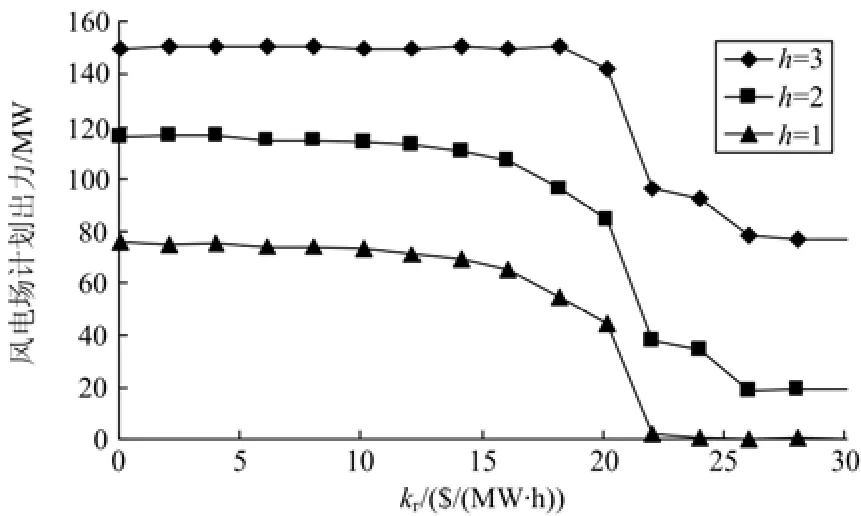
图4 风电场计划出力关于高估代价系数函数曲线Fig. 4 Scheduled wind power output as a function of up reserve cost coefficient

由图5可以看出，系统总发电成本随着pk的增大而逐渐增加。由于加大了风电浪费惩罚力度，因而会增加风电计划出力值，以降低相同风险槛值条件下所需负旋转备用量，从而避免调度过程中产生的风电低估代价LowC的进一步提升。

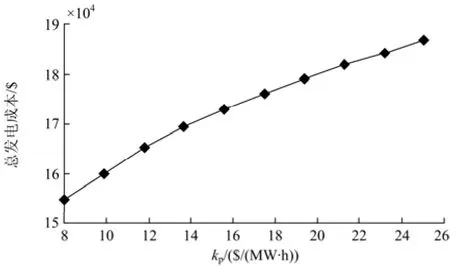
图5 总发电成本关于低估代价系数函数曲线Fig. 5 Total generation cost as a function of down reserve cost coefficient

在仿真参数选取相同的条件下用标准粒子群算法(Particle Swarm Optimization, PSO)及基本蝙蝠算法对本文所提测试系统进行仿真，标准粒子群算法可参考相关文献，本文不再阐述。图6为三种算法的寻优曲线。从图6可以看出，IBA算法在收敛速度和精度方面较前两种算法都有一定的优势。

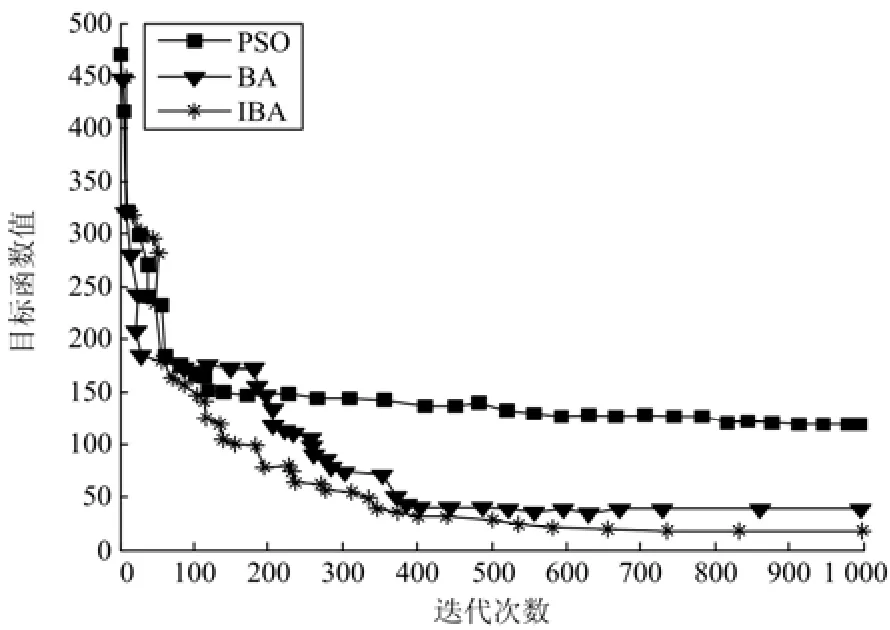
图6 三种算法的寻优曲线Fig. 6 Three kinds of optimization algorithm curve

6 结论

(1) 通过引入惯性权重系数，有效地解决了蝙蝠算法迭代后期收敛慢、易陷入局部极值的问题。

(2) 通过在约束条件中引入失负荷和风电浪费风险指标，保证了系统调度能够在合理的风险槛值内优化各个常规机组的出力计划，并可得到风电功率计划值和正、负旋转备用量。

(3) 研究表明，计及风力发电风险的系统多目标优化调度结果与系统风险槛值、不平衡代价系数等因素密切相关。在实际运行中可以有针对性地适当调整各影响因素，以选择最有效的措施实现经济性和环保性的协调优化。

[1] 杨柳青, 林舜江, 刘明波, 等. 考虑风电接入的大型电力系统多目标动态优化调度[J]. 电工技术学报, 2014, 29(10): 286-295. YANG Liuqing, LIN Shunjiang, LIU Mingbo, et al. Multi-objective dynamic optimal dispatch for large-scale power systems considering wind power penetration[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 286-295.

[2] 郭为民, 魏强, 唐耀华. 一种可在特高压或风电大量接入后减少旋转备用的新方法[J]. 电力系统保护与控制, 2014, 42(7): 1-7. GUO Weimin, WEI Qiang, TANG Yaohua. A new approach to decrease reserve demand when bulky wind power or UHV is connected[J]. Power System Protection and Control, 2014, 42(7): 1-7．

[3] 徐立中, 易永辉, 朱承治, 等. 考虑风电随机性的微网多时间尺度能量优化调度[J]. 电力系统保护与控制, 2014, 42(23): 1-8. XU Lizhong, YI Yonghui, ZHU Chengzhi, et al. Multitime scale optimal energy dispatch of microgrid considering stochastic wind power[J]. Power System Protection and Control, 2014, 42(23): 1-8.

[4] CORREIA P F, de FERREIRA J J M. Simulation of correlated wind speed and power variates in wind parks[J]. Electric Power Systems Research, 2010, 80(5)：592-598.

[5] ROY S. Market constrained optimal planning for wind energy conversion systems over multiple installation sites [J]. IEEE Transactions on Energy Conversion, 2002, 17(1): 124-129.

[6] 田中大, 李树江, 王艳红, 等. 基于小波变换的风电场短期风速组合预测[J]. 电工技术学报, 2015, 30(9): 112-120. TIAN Zhongda, LI Shujiang, WANG Yanhong, et al. Short-term wind speed combined prediction for wind farms based on wavelet transform[J]. Transactions of China Electrotechnical Society, 2015, 30(9): 112-120.

[7] DOHERTY R, MALLEY M O. A new approach to quantify reserve demand in systems with significantinstalled wind capacity[J]. IEEE Transactions on Power Systems, 2005, 20(2): 587-595.

[8] ABIDO M A. Environmental economic power dispatch using multi objective evolutionary algorithms[J]. IEEE Transactions on Power Systems, 2003, 18(4): 1529-1537.

[9] 葛晓琳, 张粒子. 考虑调峰约束的风水火随机机组组合问题[J]. 电工技术学报, 2014, 29(10): 222-230. GE Xiaolin, ZHANG Lizi. Wind-hydro-thermal stochastic unit commitment problem considering the peak regulation constraints[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 222-230.

[10] 陈珍, 胡志坚. 基于PSO-BBO混合优化算法的动态经济调度问题[J]. 电力系统保护与控制, 2014, 42(18): 44-49. CHEN Zhen, HU Zhijian. A modified hybrid PSO-BBO algorithm for dynamic economic dispatch[J]. Power System Protection and Control, 2014, 42(18): 44-49.

[11] 周玮, 孙辉, 顾宏, 等. 计及风险备用约束的含风电场电力系统动态经济调度[J]. 中国电机工程学报, 2012, 32(1): 47-55. ZHOU Wei, SUN Hui, GU Hong, et al. Dynamic economic dispatch of wind integrated power systems based on risk reserve constraints[J]. Proceedings of the CSEE, 2012, 32(1): 47-55.

[12] YANG X S, GANDOMI A H. Bat algorithm: a novel approach for global engineering optimization[J]. Engineering Computation, 2012, 29(5): 267-289.

[13] 侯贸军, 罗春辉, 隗霖捷, 等. 基于微分进化算法的水火电短期优化调度的研究[J]. 电力系统保护与控制, 2015, 43(9): 54-61. HOU Maojun, LUO Chunhui, WEI Linjie, et al. Study on short-term hydrothermal scheduling based on differential evolution[J]. Power System Protection and Control, 2015, 43(9): 54-61.

[14] 胡殿刚, 秦睿, 黄亭, 等. 基于免疫记忆粒子群优化算法的风火联合系统的多目标优化调度[J]. 高压电器, 2015, 51(6): 20-30. HU Diangang, QIN Rui, HUANG Ting, et al. Wind power integrated with thermal system multi-objective optimal dispatch based on immune memory particle swarm optimization algorithm[J]. High Voltage Apparatus, 2015, 51(6): 20-30.

(编辑 魏小丽)

Multi-objective dynamic optimal scheduling of power system considering wind power risk

YANG Jiaran1, WANG Xingcheng1, JIANG Cheng2, LUO Xiaofen3
(1. Dalian Maritime University, Dalian 116026, China; 2. State Grid Beijing Electric Power Company, Beijing 100031, China; 3. HUANENG Weihai Power Generation CO., LTD., Weihai 264205, China)

In order to solve the problem caused by the randomness of the wind power system, the load forecasting error and the probability distribution function of wind speed are introduced to establish the stochastic model of the load and wind power. Based on the in-depth analysis of the load and the random model of wind power, the cost of the wind power access to the system to maintain the stable operation of the cost of the risk is considered, and the risk of wind power loss and risk indicators are introduced. A multi-objective optimization scheduling model for power system with wind power generation risk is constructed in order to achieve the overall optimization of the system total pollution emissions and the lowest operating cost. The model is solved by using a novel bat algorithm, and the shortcomings of the algorithm are improved. The algorithm can effectively solve the problems such as slow convergence and easy to fall into local extremum. Taking large-scale wind power system as an example, the environmental and economic dispatch simulation is carried out to verify the effectiveness of the proposed model and the algorithm.

wind power; electric power systems; environmental-economic dispatch; multi-objective optimization; bat algorithm

10.7667/PSPC150905

2015-05-31；

2015-12-02

杨家然(1984-)，男，博士研究生，研究方向为新能源并网、预测、调度等；E-mail: yiran_qqqqqq@qq.com

王兴成(1956-)，男，通信作者，博士生导师，教授，研究方向为鲁棒控制理论、船舶运动控制、非线性控制、复杂系统控制、先进控制技术；E-mail: k0k690@163.com

蒋 程(1984-)，男，博士，工程师，研究方向为火力发电技术仿真及新能源并网、调度。