大规模储能电源参与电网调频研究综述

李欣然，黄际元，陈远扬，刘卫健

(1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.国网湖南省电力公司长沙供电分公司，湖南 长沙 410015；3.国网湖南省电力公司，湖南 长沙 410007)

大规模储能电源参与电网调频研究综述

李欣然1，黄际元2，陈远扬3，刘卫健1

(1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.国网湖南省电力公司长沙供电分公司，湖南 长沙 410015；3.国网湖南省电力公司，湖南 长沙 410007)

为解决风电大规模并网引起的电网调频容量不足问题，可引入储能辅助电网调频，利用其快速响应特性改善调频效果。综述了储能参与电网调频的技术现状，包括必要性与可行性分析、区域电网与储能仿真模型、协调控制方法(储能控制策略、容量配置以及经济性评估、储能-传统调频电源的联合运行)，并指出其不足之处。凝练出该研究方向的关键科学问题，并阐述了未来需重点关注的研究内容：储能用于电网调频的应用场景确定、定价机制设计及容量优化配置。

储能；调频；技术经济；仿真模型；协调控制

0 引言

风电等间歇式电源具有波动性和不确定性，且目前绝大多数间歇式电源对电网不表现出惯性，大规模接入后会显著加剧电网调频压力，尤其是当含大规模风电的电网发生冲击性负荷扰动时，传统电源的调频容量及响应速度将难以满足调频需求，该问题已成为电网接纳风电的主要制约因素之一。因此，为缓解间歇式电源并网瓶颈并改善电网频率指标，有必要引入新的辅助调频手段，而储能的快速响应特性使其在参与电网调频方面具有优势。

传统的电网调频主要包含一次调频和二次调频。在当前多数电网中，大型火电与水电机组为主要调频电源，通过不断地调整机组出力来响应电网频率变化，但是，两者均有旋转机械器件，受机械惯性和磨损等作用，影响电网安全与电能品质[1]。

近年来，利用大规模储能电源参与电网调频，已受业界广泛关注。调频的充放电周期在秒至分钟级，适合的储能类型有电池(如：锂离子电池、铅酸电池、液流电池和钠硫电池)、超级电容、飞轮和抽水蓄能等。其中，抽水蓄能的技术成熟，应用广泛，但对地理环境的依赖制约着其进一步发展。以电池储能为主的新型快速储能当前仍停留在示范阶段，且多用于改善风电场的联网运行性能，其广域调控效能未得到充分利用[2-3]。国内以中国电科院张北风光储基地、南方电网深圳宝清电池储能电站和北京石景山热电厂锂离子电池储能调频系统等大容量储能示范工程为代表，对参与二次调频功能均做了初步的测试，但尚属起步与探索阶段。而国外对大规模储能参与电网调频已展开大量示范与验证，自2008年始，A123、Xtreme Power等公司已投建多处示范项目，涉及锂离子电池等多种储能类型，包含从1 MW(功率)/0.5 MWh(容量)到20 MW/5 MWh等一系列容量，已取得一定成果[4-5]。国内外具有调频功能的部分储能示范工程如表1所示。

表1 国内外具有调频功能的部分储能示范工程Table 1 Some demonstration projects of energy storage system with frequency regulation function around the world

这类研究与示范工程表明，大规模储能技术今已具备电网调频应用能力，且该应用是储能在电力领域中最接近商业运营的典型应用。从电网运行需求全局角度，如何在电网调频中利用好储能是当前的关键问题。为此，本文综述了储能参与电网调频的研究现状并指出其不足之处，凝练出关键科学问题并给出未来需研究的若干重要问题。

1 必要性与可行性问题

1.1 必要性问题

为了解决储能参与电网调频的必要性问题，有学者从风电功率波动特性、高比例风电接入对电网频率的影响出发进行了相关工作。

部分文献利用时/频域分解法研究风电功率波动特性，并分析不同风电渗透率和不同风事件对电网频率的影响程度。文献[6]在时域中通过计算风电功率爬坡率，统计对电网频率影响较大的风电功率波动所占比例，而在频域中通过小波变换和经验模态分解法对风电功率波动频段进行划分，并依据对电网频率的影响程度排序。文献[7]划分四种典型风事件，仿真分析了电网调频动态仿真模型中的参数灵敏度及风电场接入位置对电网频率的影响，指出电网应储备足够的爬坡容量以应对各种风事件。文献[8-9]提出大规模风电接入对电网频率影响程度的评估方法。其中，文献[8]利用t-location概率分布模型描述风电功率随机波动特性，采用序贯蒙特卡洛法模拟时序风电功率序列，基于某区域电网分析可知，风电功率波动范围随时间尺度的增大而增大，风电接入规模占电网总装机容量比例较小时，即使最严重波动情况下的最大频率偏差也不会导致电网频率动态越限；文献[9]利用所推导的结合了风电功率波动与负荷波动的电网功率波动概率函数，并依据与调频相关的五个典型指标(惯性响应、静态频率偏差、一/二次调频调整速度和调频备用需求)，通过算例分析得知，风电功率波动对电网频率的影响程度与电网独立/互联及调频尺度相关，且对独立电网的惯性、一次调频和静态频率偏差的影响要大于互联电网。

总体说来，现有研究尚存在以下问题：未深入分析风电场(群)功率波动特征，因风电功率波动实质上是一个正态随机过程，其包含比较复杂的时序过程，如何在前述分析过程中考虑不确定性的随机过程尚待研究；同时，未明确认识对电网频率影响较为严重的风电功率爬坡特性，特别是对风电场集群功率波动(尤其是对电网危害较大的上行爬坡)对电网频率的影响尚无研究，无法有效揭示风电接入对电网频率稳定的影响机理，未定量评估电网中风电比例达何种高度时对电网调频有何种程度的影响，进而难以确定引入新型快速储能的合适应用场景。

1.2 可行性问题

为了解决储能参与电网调频的可行性问题，有学者从技术和经济价值评估角度展开了相关研究。

在技术可行性方面，储能的价值主要体现在其相比传统调频电源的高效性上。目前尚无文献公开报道储能参与一次调频的高效性，对二次调频的相关研究表明储能比传统调频电源高效数倍。美国某实验室的研究报告指出飞轮储能的调频能力为水电机组的1.7倍，燃气机组的2.7倍，火电机组和联合循环机组的近20倍[10]；基于含储能的区域电网调频动态模型，且假设火电机组的爬坡速率为4% p.u./ min，对比可知20 MW电池储能的调频能力与187.5 MW火电机组等效，前者比后者高效约9倍[11]；即使忽略火电机组的爬坡速率约束，对比可知，10 MW/3.66 MWh电池储能的调频能力与36 MW的火电机组等效，前者高效3.6倍[12]。

在经济可行性方面，目前尚无专门的政策支持储能进入调频市场，研究中通常利用简易的成本效益分析来评估其经济价值。评估中的成本考虑全寿命周期内的投资、运行和维护费用，效益考虑调频补偿费用，包括依合同签订的调频功率($/MW)对储能参与一次调频计费，依调频容量和调频电量($/MWh)、上行爬坡和下行爬坡功率($/MW)分别对储能参与二次调频计费。

对一次调频，文献[13]通过简易的成本效益分析初步对比了铅酸、钒液流和钠硫等电池储能参与一次调频和调峰的经济性，可知在一定范围储能容量内，未来3～5年间电池储能在一次调频方面最具应用潜力；文献[14]提出了虚拟电厂(由储能和风电场联合组成)中储能的选型方法，以一次调频为例，依储能运行的年累计运行成本，对比了电池(锂离子、铅酸、钒液流和钠硫电池等)、超级电容和飞轮等储能类型的经济性，可知具备长日历寿命和低自放电率等优势的钛酸锂和磷酸铁锂离子电池的技术经济性最佳[15]。

对二次调频，仅从成本角度，前述文献[4]由简单估算知储能的年平均投资成本为火电机组的2.7～4.7倍，但指出相比火电机组，储能在运行和维护成本上具有优势；考虑储能的二次调频效益，文献[16]分析钠硫电池储能在调频、风电调峰和爬坡控制中的效益，其中参与电网调频的收益由能量市场实时价格决定，对比可知其在参与调频时的价值最高，相同功率下较小的容量能获得更大的效益；文献[17]将钒液流电池储能用于德克萨斯州电网调频，构建储能的动态等效模型及在运行周期内的效益模型，相关经济参数包括预测上行爬坡和下行爬坡价格($/(MW•h))、实时能量市场价格($/(MW•min))，约束条件为日调频服务结束时储能的荷电状态(State of Charge, SOC)不小于50%，仿真分析可知其用于调频的价值约为1 211～1 871 $/kW，而1 MW/1 MWh和1 MW/4 MWh储能的成本分别约为1 460～1 613 $/kW和1 919～3 279 $/kW，可见储能在该调频应用下的成本和效益已比较接近。而随着技术的成熟和成本的降低，储能的竞争优势会进一步提升[18]。

现有研究仅从技术和经济角度简单分析了储能相比传统调频电源的高效性和储能的潜在经济优势，究其原因，一是缺乏对储能调频成本的明确认识，二是未能深入理解储能的多时间尺度特征，无法合理量化它对电网的经济价值。应当指出，完整的成本效益还应包括：全寿命周期内储能的替换成本(因储能报废导致)，在调频中储能本身功率和容量的直接效益及改善电网其他设备运行条件所带来的间接效益、减少电网备用容量所带来的备用效益和提高风电等间歇式电源渗透率所带来的环境效益。此外，还有储能设备老化、储能控制方式、政策和电力市场博弈等对储能成本和效益的影响。因此，为保证投资经济性和运行收益，必须建立面向电网调频的不同形式储能的技术-经济模型，提炼出储能用于电网调频的主导技术和经济特征，以便于建立合适的储能调频价格机制，进而为推动其进入调频市场提供依据。

2 区域电网与储能仿真模型

对区域电网，国内外一般基于区域等效方法，描述区域电网和传统电源的频率特性，即将电网元件模型转换为传递函数形式，搭建区域电网调频动态模型，再展开仿真实验[1]。区域电网调频动态模型示意图如图1所示，其主要包括：调速器及涡轮机模型、负荷扰动模型、惯性和负荷阻尼控制、ACE信号计算及处理等环节。

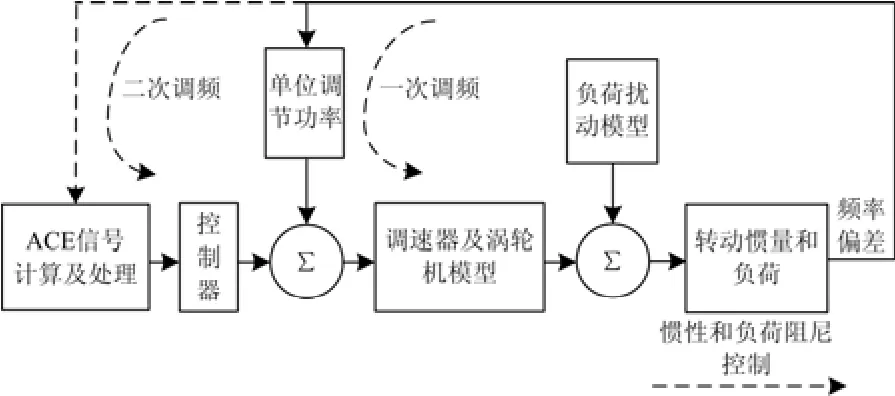
图1 区域电网调频动态模型示意图Fig. 1 Schematic of equivalent model for regional grids

上述区域电网调频动态模型未区分对不同规模、不同电压等级电网的适用性，且该模型中传统电源的经典模型已无法充分描述现代新型机组动态特性。

在储能方面，以电池储能电源为例，其由电池储能设备与功率转换系统(Power Conversion System, PCS)所构成，储能模型主要包括单体元件模型和PCS及其控制方法模型[19-20]。国外为满足电池管理系统的需求而建立单体元件模型，包括理想模型、一阶、二阶和四阶模型等[21]。调频研究中广泛采用一阶惯性环节与控制增益的乘积来描述电池储能参与电网调频的行为特征[22]，如图2所示。图中，控制信号∆cons(s)一般为频率偏差或区域控制误差等；增益KE模拟了Δcons(s)与储能电源出力ΔPE(s)之间的转换关系；时间常数TE描述了电池本身特性和PCS环节的延时效应。

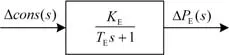
图2 电池储能电源的传递函数模型Fig. 2 Transfer function model for battery energy storage

近年来，国内同样认识到建立适合电网仿真需求的储能模型的重要性。文献[23]仅考虑PCS的内外环控制策略而建立电池储能的通用模型；文献[24]提出利用基于戴维南等效电路的传递函数模型描述参与电网调频的电动汽车与电网互动技术(Vehicle to Grid, V2G)储能模型。

目前，调频研究中采用的储能模型还相当滞后于实际工程需求。上述分析表明对于电池储能模型研究，过于侧重单体元件自身的动态行为，或过于侧重电网连接的动态行为。前者模型太过复杂，在电网仿真分析计算中应用难度较大；后者模型太过简化，对单体元件自身的动态特性考虑不足，且未能反映出单体元件到储能设备的过渡，缺乏一种既能准确反映储能自身特性，又能满足调频研究需求的仿真模型。

3 协调控制方法

3.1 储能参与电网调频的控制策略

储能参与电网调频控制策略的相关概念包括控制模式、动作时机与深度。其中，控制模式为参与调频的方式；动作时机为投入和退出调频运行状态的时刻；动作深度为参与调频的出力大小[25]。

储能的动态响应特性主要由PCS控制主导，故控制PCS模拟传统调频电源的下垂特性即能实现其参与一次调频，定义储能动作深度与频率增量之比为虚拟单位调节功率系数，记为KE。对集中式电池储能，文献[26]假设电池储能的额定功率为Prated，以±20 mHz为一次调频死区，即确定了其动作时机，同时控制电池储能在±20～±200 mHz内线性出力，则KE为(Prated/180) MW/mHz，即可确定其动作深度；文献[27]提出利用频率变化过程中的频差变化率和频率偏差为决策变量，当频差变化率越过设定的限值时，控制电池储能以额定功率输出，当频率开始恢复时变换至下垂控制(KE为经验值)，图3即为该方法的示例。图中，PEF为储能参与一次调频的动作深度，∆fDB为调频死区，∆f0为初始频率偏差(一般取为0)，KE1和KE2分别对应储能放电和充电时的虚拟单位调节功率系数；若负荷突然增加引起了频率下降，设?为设定的频差变化率限值(负数)，当dΔf/dt0 Hz/s且|Δf|>∆fDB/2时，储能依据下垂控制放电(对应图中的实线段2)。对分散式储能V2G，文献[28]提出考虑电动汽车电池储能荷电状态(SOC)因素的变KE策略，此处KE为以SOC和充放电状态变量表示的分段函数，该策略需首先确定KE最大值Kmax、SOC运行参考值SOCref及较高值SOChigh、较低值SOClow，该方法在灵活满足用户充电需求前提下，可在一定程度上改善调频效果。

图3 储能参与一次调频的方法示例Fig. 3 An example method of energy storage system participating in primary frequency regulation

储能承担部分调频信号可参与二次调频，定义储能的参与因子(Participation Factor, PF)为αE。对集中式储能，调频信号分配方式主要为按时/频域分配和按动态比例分配。前者分析区域控制误差(Area Control Error, ACE)信号在时/频域内的特征，由储能承担短时分量(高频分量)，由传统调频电源承担长时分量(低频分量)[29-30]。后者依托区域电网调频动态模型，文献[31]将区域控制需求(Area Regulation Requirement, ARR)信号划分为正常调节区、警戒区和紧急区，依不同的优先级，将其分配给储能、V2G和传统调频电源。前述文献[12]基于可表征电池储能动态调频容量(Dynamic Available AGC, DAA)评估指标，对比依ACE信号和依ARR信号的两种动态分配方式的短期和中长期调频效果，综合可知，基于ACE信号的独立分配策略效果更佳，此时储能无需经过传统的低通滤波环节，但需增加独立的控制器，图4即为该方法的示例。图4中，PEA为储能参与二次调频的动作深度；标号1和2分别表示储能接受ACE和ARR信号的分配方式(ACE信号经由滤波器和PI控制器形成ARR信号)；参与因子αE需依据相关原则进行优化设计。

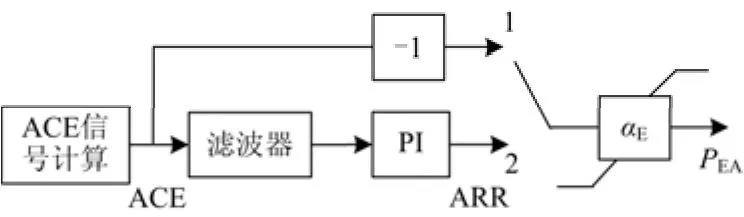
图4 储能参与二次调频的方法示例Fig. 4 An example method of energy storage system participating in secondary frequency regulation

由上可知，已有研究仅初步探索了储能参与调频的控制策略，仍存在如下不足之处：对参与一次调频，未明确储能的控制模式，也未深入分析其如何参与；对参与二次调频，研究集中于对ACE信号的分析以及考虑区域电网调频动态模型的ARR分配，且按时/频域分配的方法在储能层面未考虑荷电状态SOC管理，在电网层面也未充分利用储能优势，而按动态比例分配的方法未从机理层面分析储能该如何参与，导致无法充分利用储能容量及其技术优势。

3.2 容量配置以及经济性评估

面向电网调频，储能容量配置研究主要基于实测信号和区域电网调频动态模型展开。从实测频率和调频信号出发，依前者确定储能参与一次调频的动作深度，依后者中的高频/短时分量确定储能参与二次调频的动作深度，再通过确定的动作深度计算储能在运行周期内的能量值，以最大能量差作为配置的额定容量；从区域电网调频动态模型出发，依设定的调频评估指标要求确定所需储能功率和容量。经济性评估需构建储能的经济运行模型，包括经济最优目标函数及约束条件，容量作为其中的一个决策变量，采用智能算法等进行寻优求解，常用的优化目标为全寿命周期成本最低或者净效益最高等。储能参与调频的容量配置与经济性评估示意图如图5所示。

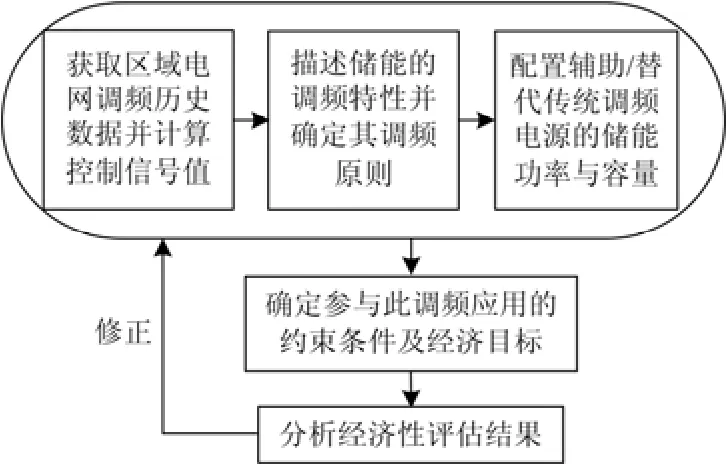
图5 储能参与调频的容量配置与经济性评估示意图Fig. 5 Schematic of capacity allocation and economic evaluation of energy storage system in frequency regulation

图5 中，首先从实际区域电网调频历史数据出发，统计出相应的频率偏差和区域控制误差信号值；然后在已知的频率偏差允许值等电网调频要求的基础上，描述储能的调频特性，确定储能的调频原则，即建立起储能的一次调频动作深度与频率偏差，二次调频动作深度与区域控制误差之间的关联关系，进而配置出相应的储能容量，基于此容量配置结果分析储能在辅助调频领域的经济价值，同时又反过来进一步指导与修正储能的容量配置方法，得出性能/成本最优的储能容量配置值。

对一次调频的容量配置，基于实测频率信号，文献[32]通过分析分散在11个星期的频率信号的特征，设计电池储能的功率与容量，并用调频死区和SOC控制回路来保证其SOC保持在一个合理的区间内，以减轻循环运行对电池储能寿命的影响。文献[33]探讨如何最小化所配储能容量，采用在储能动作深度上实时叠加额外充放电功率的策略，克服储能控制信号在运行周期内偏离零均值的影响，但该方法会导致储能运行成本增加。依托区域电网调频动态模型，文献[34]将风电等效为负荷，研究储能对频率偏差和联络线功率偏差的影响，并利用频率偏差的均方根值和绝对最大值两项指标来配置储能容量。

对二次调频的容量配置，基于从调度中心获得的实际调频信号，文献[35]利用定时间常数滤波法将该信号划分为高频和低频部分，用储能承担高频分量，据此分析对储能的调频容量需求和爬坡容量需求。依托区域电网调频动态模型，文献[36]储能实时补偿传统调频机组因爬坡限制而未能实现的部分功率，并提出保证电池储能的SOC在一个合理区间内的控制策略，研究可知，当风电和储能安装在同一区域时达到的调频效果最优，且所配储能容量最小。

前述文献[26]依据简易的成本效益模型，以含水电厂、火电厂及风电的独立电网(总发电容量为450 MW，风电渗透率20%)为背景，以电池储能产生的年效益最大为目标，建立经济评估模型，并提出一种容量和运行方式优化方案，用净现值法评估寿命周期(20年)内储能配置方案的经济性。文献[37]针对风储联合参与一次调频应用，提出一种基于经济性最优的储能容量配置方法，以参与调频时储能所需的功率和容量最小为目标，运用线性规划原理形成相应的成本效益模型，并基于英国电网某50 MW风电场分析可知配置5.3 MW/3 MWh的VRB就能满足电网调频需求且最大化风电运营商的效益，此时储能的功率约为风电场额定功率的10%，持续时间约为30 min。

常用的储能参与电网调频的经济评估模型如式(1)所示，其中考虑了全寿命周期内储能参与电网调频的成本与效益，并通过净现值法将其折算到项目投资的初始时刻(第零年)。

式中：PNET为净效益现值，一般以其值最大为储能参与电网调频容量配置的经济性优化目标；NRES为效益现值；CLCC为成本现值；PCAPACITY为日备用功率效益；PENERGY为日调频电量效益；N为一年的调频时长，通常以300天计；TLCC为全寿命周期；r为折现率；Cinv、CO&M和Cscr分别为储能的年投资成本、运维成本和报废处理成本。

储能的容量配置当前多基于经验分析，适应性和可行性不强，较多关注单一类型储能的容量配置，且一般将风电等效为负荷，故所配容量缺乏足够的说服力；参与二次调频的储能容量配置鲜有文献提及，更无涉及混合储能参与调频方面的研究；经济性评估无公认的目标函数和求解算法，计算过程较复杂。应当指出，在保证频率控制满足要求的前提下，最小化调频成本至关重要，而储能容量是决定其成本的核心因素，因此，在储能参与多任务的前提下，如何处理好调频要求与储能技术性和经济性间的关系至关重要。

3.3 储能与传统调频电源的联合运行

一般从传统调频控制、储能与传统调频电源的协调控制角度展开研究。

传统调频控制研究集中于整定PI控制器参数和利用高级控制方法替代PI，前者采用遗传算法、人工神经网络和神经模糊推理等智能算法动态整定，仿真比较各个自适应控制器在不同负荷水平和电网参数条件下的性能，后者利用模型预测控制或自适应模糊控制等高级控制方法，对电网的参数不确定性、延时及控制过程中的非线性环节进行优化设计，取得比PI控制器更佳的控制效果[38]。

通过新型控制方法协调储能与传统调频电源，不仅能充分利用各自的技术优势，还能有效减少电网频率及联络线功率的波动， 且控制效果优于PI控制器。文献[39]面向微网提出基于鲁棒控制的储能调频控制策略，运用μ-综合相关理论，计及电网参数不确定性、测量噪声等对控制效果的影响，对控制偏差与控制输入信号采取不同加权函数，使储能和传统调频电源分别承担高频和低频信号，并保持储能SOC维持在50%附近，仿真结果表明所设计控制器有效，能较好地应对电网参数变化及噪声影响。文献[40]提出一种基于模糊控制的电池储能辅助AGC调频策略，该控制器的输入量为ACE及其变化率，输出量为电池储能的动作深度，采用此策略能使储能快速响应ACE变化，并在火电机组逐渐增加出力时减少储能出力，直至电网达到新的平衡态时储能退出运行，仿真表明此策略有效，且能减少储能所需配置的容量。文献[41]提出一种利用二次规划法分配调频信号的策略，该策略控制飞轮储能跟踪快速变化的调频信号，并在其接近于满充或满放时，由传统调频电源弥补其不足，可延长前者的使用寿命并提高后者的运行效率。此外，有学者研究储能、传统调频电源与风力机联合调频，文献[42]提出基于SOC反馈的风-储联合调频控制策略，该策略需要实时监测电网频率偏差和储能SOC状态，由电池储能优先响应电网频率变化，当其SOC值位于不同区间时，通过协调风力机与火电机组参与调频，使储能SOC维持在50%附近，为下一时刻调频任务做好准备。

可见，国内外对储能与传统调频电源联合运行的研究尚属起步阶段。如何在模型中更合理地体现储能的技术优势及如何协调好混合储能的运行亟需深入研究，同时可结合控制理论对(多)区域电网调频动态模型进行分析，运用新型智能控制方法解决储能参与调频问题，因为储能与传统调频电源的联合运行是储能工程化应用的基础。

应当指出，从电网运行需求全局角度，如何结合和兼顾储能、风电以及传统调频电源的技术经济特性，形成多时间尺度的协调控制策略是电网面临的一个重要问题。此外，储能应用于电网一、二次调频的协联控制技术也尚待研究。

4 关键科学问题

综上可知，在大规模储能用于电网调频方面，国外已开展了不少基础理论工作，而国内理论分析开展较少，应用示范也属起步阶段，且国内网架和能源结构与国外相差甚远，故亟需探索符合我国电网特点的储能调频技术，加大基础理论研究及工程示范力度，以利用储能更好地服务新一代“坚强”“智能”电网。围绕前述问题，凝练出关键科学问题如下：

(1) 储能参与电网调频的必要性和可行性问题。需从受风电和光伏发电出力波动性和不确定性影响的电网综合负荷特性和与之对应的电网频率波动特性(尤其是频率波动的频谱特性)出发，结合储能的技术与经济特性，研究储能参与电网调频的应用场景，提出相应的场景划分方法与指标，进而构建考虑技术与经济因素的储能参与电网调频的必要性和可行性综合评估方法和评估指标体系。

(2) 储能参与调频的协调控制问题。科学问题(1)解决电网调频要不要储能参与的问题，科学问题(2)则解决怎样参与的问题。其核心点在四个方面：一是参与的时机，二是调整(充放电)的深度，三是参与电网调频的储能的类型和容量如何配置，四是(混合)储能和传统调频电源间如何协调。

(3) 储能参与电网调频时的仿真模型和仿真方法问题。尽管储能的模型已多有研究，但对调频应用而言，构建合理的仿真模型仍为首要解决的基础性和关键性问题。

5 结论

在推动储能调频的工程应用研究中，除需显著提高储能自身的集成技术和大幅降低成本之外，还需考虑以下几点：

(1) 从高比例风电接入下的电网频率特性以及传统调频电源的固有缺陷角度出发，依据电网调频能力以及准稳态运行要求等不同电网约束，提出电网对风电功率波动的合理要求范围，基于此提炼有价值的调频应用场景以体现储能的不可替代性。

(2) 提出能够反映储能用于电网调频应用技术条件的主导特征参数，建立储能规模化应用的广义经济效益/成本计算模型，形成储能的综合技术与经济条件评估模型，并研究指标权重赋值方法；构建储能调频的考核指标，提出相应的辅助服务定价机制，平衡储能投资方、其他发电方与电网公司的多方收益。

(3) 从储能改善电网频率特性的机理入手，研究计及广域风电场间出力耦合条件的区域电网储能配置与布点原则，确定合适的综合效益最优目标及电网调频要求并提出所需最小储能容量的计算方法和模型；通过数学规划原理提出考虑储能动作时机和深度的控制策略；研究(混合)储能-传统调频电源-间歇式电源三者的的协调优化控制策略与方法。

未来可开发储能参与电网调频的分析与控制软件，为该应用提供辅助决策分析和仿真工具。

[1] KUNDUR P. 电力系统稳定与控制[M]. 北京: 中国电力出版社, 2002: 389-410.

[2] 冯江霞, 梁军, 冯益坤. 基于风电功率min级分量波动特性的风电场储能容量优化计算[J]. 电力系统保护与控制, 2015, 43(3): 1-6. FENG Jiangxia, LIANG Jun, FENG Yikun. Optimization calculation of wind farm storage capacity based on minute-scale wind power characteristic[J]. Power System Protection and Control, 2015, 43(3): 1-6.

[3] 江润洲, 邱晓燕, 陈光堂. 风电场混合储能系统优化配置方法[J]. 电力系统及其自动化学报, 2015, 27(1): 37-42, 48. JIANG Runzhou, QIU Xiaoyan, CHEN Guangtang. Optimal configuration method of hybrid energy storage system for wind farm[J]. Proceedings of the CSU-EPSA, 2015, 27(1): 37-42, 48.

[4] 陈大宇, 张粒子, 王澍, 等. 储能在美国调频市场中的发展及启示[J]. 电力系统自动化, 2013, 37(1): 9-13. CHEN Dayu, ZHANG Lizi, WANG Shu, et al. Development of energy storage in frequency regulation market of United States and its enlightenment[J]. Automation of Electric Power Systems, 2013, 37(1): 9-13.

[5] 张川, 杨雷, 牛童阳, 等. 平抑风电出力波动储能技术比较及分析[J]. 电力系统保护与控制, 2015, 43(7): 149-154. ZHANG Chuan, YANG Lei, NIU Tongyang, et al. Comparison and analysis of energy storage technology to balance fluctuation of wind power output[J]. Power System Protection and Control, 2015, 43(7): 149-154.

[6] MIAO Fufeng, TANG Xisheng, QI Zhiping. Fluctuation feature extraction of wind power[C] // IEEE Innovative Smart Grid Technologies-Asia, Tianjin, May 21-24, 2012: 1-5.

[7] BANAKAR H, LUO Changling, OOI B T. Impacts of wind power minute-to-minute variations on power system operation[J]. IEEE Transactions on Power Systems, 2007, 23(1): 150-160.

[8] 崔杨, 刘嘉, 严干贵, 等. 联网风电功率波动对电力系统频率影响评估[J]. 太阳能学报, 2014, 35(4): 617-623. CUI Yang, LIU Jia, YAN Gangui, et al. Effect of on-grid wind power fluctuation on frequency stability of electric power system[J]. Acta Enegiae Solaris Sinica, 2014, 35(4): 617-623.

[9] 丁立, 乔颖, 鲁宗相, 等. 高比例风电对电力系统调频指标影响的定量分析[J]. 电力系统自动化, 2014, 38(14): 1-8. DING Li, QIAO Ying, LU Zongxiang, et al. Impact on frequency regulation of power system from wind powerwith high penetration[J]. Automation of Electric Power Systems, 2014, 38(14): 1-8.

[10] LIN J, DAMATO G, HAND P. Energy storage-a cheaper, faster and cleaner alternative to conventional frequency regulation[R]. Strategen, CESA, 2011: 1-15.

[11] SASAKI T, KADOYA T, ENOMOTO K. Study on load frequency control using redox flow batteries[J]. IEEE Transactions on Power Systems, 2002, 19(1): 660-667.

[12] CHENG Yunzhi, TABRIZI M, SAHNI M, et al. Dynamic available AGC based approach for enhancing utility scale energy storage performance[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 1070-1078.

[13] OUDALOV A, CHARTOUNI D, OHLER C, et al. Value analysis of battery energy storage applications in power systems[C] // IEEE Power Systems Conference and Exposition, Atlanta, October 29-November 1, 2006: 2206-2211.

[14] SWIERCZYNSKI M, STROE D I, STAN A I, et al. Selection and performance-degradation modeling of LiMO2/Li4Ti5O12 and LiFePO4/C battery cells as suitable energy storage systems for grid integration with wind power plants: an example for the primary frequency service[J]. IEEE Transactions on Sustainable Energy, 2014, 5(1): 90-100.

[15] SWIERCZYNSKI M, STROE I, STAN A I, et al. Lifetime and economic analyses of lithium-ion batteries for balancing wind power forecast error[J]. International Journal of Energy Research, 2015, 39: 760-770.

[16] TEWARI S, MOHAN N. Value of NAS energy storage toward integrating wind: results from the wind to battery project[J]. IEEE Transactions on Power Systems, 2013, 28(1): 532-541.

[17] FARES R L, MEYERS J P, WEBBER M E. A dynamic model-based estimate of the value of a vanadium redox flow battery for frequency regulation in Texas[J]. Applied Energy, 2014, 113: 189-198.

[18] 杨舒婷, 曹哲, 时珊珊, 等. 考虑不同利益主体的储能电站经济效益分析[J]. 电网与清洁能源, 2015, 31(5): 89-93, 101. YANG Shuting, CAO Zhe, SHI Shanshan, et al. Analysis on economic benefits of storage power station considering different interest-subjects[J]. Power System and Clean Energy, 2015, 31(5): 89-93, 101.

[19] 曹生允, 宋春宁, 林小峰, 等. 用于电池储能系统并网的PCS控制策略研究[J]. 电力系统保护与控制, 2014, 42(24): 93-98. CAO Shengyun, SONG Chunning, LIN Xiaofeng, et al. Study of PCS’s control strategy for battery energy storage grid-connected system[J]. Power System Protection and Control, 2014, 42(24): 93-98.

[20] 常丰祺, 郑泽东, 李永东. 一种新型混合储能拓扑及其功率分流算法[J]. 电工技术学报, 2015, 30(12): 128-135. CHANG Fengqi, ZHENG Zedong, LI Yongdong. A novel hybrid energy storage topology and its power sharing algorithm[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 128-135.

[21] KIM T, QIAO Wei. A hybrid battery model capable of capturing dynamic circuit characteristics and nonlinear capacity effects[J]. IEEE Transactions on Energy Conversion, 2011, 26(4): 1172-1180.

[22] MU Yunfei, WU Jianzhong, EKANAYAKE J, et al. Primary frequency response from electric vehicles in the great Britain power system[J]. IEEE Transactions on Smart Grid, 2013, 4(2): 1142-1150.

[23] 李妍, 荆盼盼, 王丽, 等. 通用储能电源数学模型及其PSASP建模研究[J]. 电网技术, 2012, 36(1): 51-57. LI Yan, JING Panpan, WANG Li, et al. A mathematical model of versatile energy storage system and its modeling by power system analysis software package[J]. Power System Technology, 2012, 36(1): 51-57.

[24] 黄媛, 刘俊勇, 陈井锐, 等. 计及电动汽车入网的负荷频率控制[J]. 电力系统自动化, 2012, 36(9): 24-28. HUANG Yuan, LIU Junyong, CHEN Jingrui, et al. Load frequency control considering vehicle to grid[J]. Automation of Electric Power Systems, 2012, 36(9): 24-28.

[25] 黄际元, 李欣然, 曹一家, 等. 考虑储能参与快速调频动作时机与深度的容量配置方法[J]. 电工技术学报, 2015, 30(12): 454-464. HUANG Jiyuan, LI Xinran, CAO Yijia, et al. Capacity allocation of energy storage system considering its action moment and output depth in rapid frequency regulation [J]. Transactions of China Electrotechnical Society, 2015, 30(12): 454-464.

[26] MERCIER P, CHERKAOUI R, OUDALOV A. Optimizing a battery energy storage system for frequency control application in an isolated power system[J]. IEEE Transactions on Power Systems, 2009, 24(3): 1469-147.

[27] DELILLE G, FRANCOIS B, MALARANGE G. Dynamic frequency control support by energy storage to reduce the impact of wind and solar generation on isolated power system’s inertia[J]. IEEE Transactions on Sustainable Energy, 2012, 3(4): 931-939.

[28] LIU Hui, HU Zechun, SONG Yonghua, et al. Decentralized vehicle-to-grid control for primary frequency regulation considering charging demands[J]. IEEE Transactions onPower Systems, 2013, 28(3): 3480-3489.

[29] MAKAROV Y V, DU Pengwei, KINTNER-MEYER M C W, et al. Sizing energy storage to accommodate high penetration of variable energy resources[J]. IEEE Transactions on Sustainable Energy, 2012, 3(1): 34-40.

[30] 胡泽春, 谢旭, 张放, 等. 含储能资源参与的自动发电控制策略研究[J]. 中国电机工程学报, 2014, 34(29): 5080-5087. HU Zechun, XIE Xu, ZHANG Fang, et al. Research on automatic generation control strategy incorporating energy storage resources[J]. Proceedings of the CSEE, 2014, 34(29): 5080-5087.

[31] ZHONG Jin, HE Lina, LI Canbing, et al. Coordinated control for large-scale EV charging facilities and energy storage devices participating in frequency regulation[J]. Applied Energy, 2014, 123: 253-262.

[32] HOLMBERG M T, LAHTINEN M, MCDOWALL J, et al. SVC light with energy storage for frequency regulation[C] // IEEE Innovative Technologies for an Efficient and Reliable Electricity Supply, Waltham, September 27-29, 2010: 317-324.

[33] BORSCHE T, ULBIG A, KOLLER M, et al. Power and energy capacity requirements of storages providing frequency control reserves[C] // IEEE Power and Energy Society General Meeting, Vancouver, July 21-25, 2013: 1-5.

[34] OTA Y, TANIGUCHI H, NAKAJIMA T, et al. Effect of autonomous distributed vehicle-to-grid (V2G) on power system frequency control[C] // IEEE 5th International Conference on Industrial and Information System, India, July 29-August 1, 2010: 481-485.

[35] LEITERMANN O. Energy storage for frequency regulation on electric grid[D]. Massachusetts: Massachusetts Institute of Technology, 2012.

[36] LIANG Liang, ZHONG Jin, JIAO Zaibin. Frequency regulation for a power system with wind power and battery energy storage[C] // IEEE International Conference on Power System Technology, Auckland, October 30-November 2, 2012: 1-6.

[37] JOHNSTON L, DIAZ-GONZALEZ F, GOMISBELLMUNT O, et al. Methodology for the economic optimization of energy storage systems for frequency support in wind power plants[J]. Applied Energy, 2015, 137: 660-669.

[38] YOUSEF H A, AL-KHARUSI K, ALBADI M H, et al. Load frequency control of a multi-Area power system: an adaptive fuzzy logic approach[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1822-1830.

[39] HAN Yi, YOUNG P M, JAIN A, et al. Robust control for microgrid frequency deviation reduction with attached storage system[J]. IEEE Transactions on Smart Grid, 2015, 6(2): 557-565.

[40] 丁冬, 刘宗歧, 杨水丽, 等. 基于模糊控制的电池储能系统辅助AGC调频方法[J]. 电力系统保护与控制, 2015, 43(8): 81-87. DING Dong, LIU Zongqi, YANG Shuili, et al. Battery energy storage aid automatic generation control for load frequency control based on fuzzy control[J]. Power System Protection and Control, 2015, 43(8): 81-87.

[41] JIN Chunlian, LU Ning, LU Shuai, et al. A coordinating algorithm for dispatching regulation services between slow and fast power regulating resources[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 1043-1050.

[42] DANG Jie, SEUSS J, SUNEJA L, et al. SOC feedback control for wind and ESS hybrid power system frequency regulation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(1): 79-86.

(编辑 魏小丽)

Review on large-scale involvement of energy storage in power grid fast frequency regulation

LI Xinran1, HUANG Jiyuan2, CHEN Yuanyang3, LIU Weijian1
(1. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China; 2. State Grid Hunan Electric Power Corporation Changsha Power Supply Company, Changsha 410015, China; 3. State Grid Hunan Electric Power Corporation, Changsha 410007, China;)

To solve the capacity shortage problem in power grid frequency regulation caused by large-scale integration of wind power, energy storage system (ESS), with its fast response feature, can be introduced as a supplementary means to frequency regulation to achieve better effects. The technical state of energy storage’s involvement in power grid fast frequency regulation is reviewed, including its necessity and feasibility, simulation models of regional grids and ESS, coordination control methods (ESS’s control strategy, capacity configuration and economic evaluation, and joint operation of ESS and conventional generators), and its shortcomings are analyzed. The scientific issues in this field are refined, and important issues to be focused in this area are set forth, i.e., application scenarios analysis, pricing mechanism design and optimal capacity allocation of ESS in frequency regulation.

This work is supported by National Basic Research Program of China (973 Program) (No. 2012CB215106) and National Natural Science Foundation of China (No. 51477043).

energy storage; frequency regulation; technical-economy; simulation model; coordination control

10.7667/PSPC150958

2015-06-08；

2015-12-10

李欣然(1957-)，男，博士，教授，研究方向为电力系统分析控制、负荷建模；E-mail: lixinran1013@qq.com

黄际元(1988-)，男，通信作者，博士，研究方向为储能建模及其在电力系统中的应用；E-mail: hjycm@hnu.edu.cn

陈远扬(1987-)，男，硕士，研究方向为电力系统运行控制与调度。E-mail: 283133469@qq.com

国家重点基础研究发展(973)计划(2012CB215106);国家自然科学基金项目(51477043)