考虑塔影与风切变的永磁同步风电系统最大风能跟踪控制策略

刘 军，周飞航，刘 飞,2

(1.西安理工大学自动化学院，陕西 西安 710048；2.武警工程大学，陕西 西安 710048)

考虑塔影与风切变的永磁同步风电系统最大风能跟踪控制策略

刘 军1，周飞航1，刘 飞1,2

(1.西安理工大学自动化学院，陕西 西安 710048；2.武警工程大学，陕西 西安 710048)

为了保证风电机组高效稳定运行，通过在转矩控制环节中引入模糊变增益的转速补偿转矩，有效地减轻了由塔影效应、风切变、风速中的随机脉动分量引起的风力机输出的机械转矩波动与按照最优叶尖速比法计算的参考转速的波动对永磁同步风力发电系统的影响，抑制了风电系统的低频震荡并保证了系统的稳定性。当考虑到轴系的摩擦损耗时，为了真正地实现最大风能跟踪，通过对最优叶尖速比进行修正，得出最大电磁功率所对应的准确的参考转速，使得机组运行在最大电磁功率对应的工作点处。在Matlab/Simulink下构建了直驱永磁同步风电系统的详细仿真平台，验证了该方法的正确性与有效性。

塔影效应；风切变；永磁同步风力发电系统；低频振荡；叶尖速比

0 引言

风能作为最有潜力的可再生能源，越来越多地得到了世界各地的关注，根据数据显示全球风能市场每年增长41%[1]。近些年来，人们对风电系统的研究主要集中在提高风力发电机的容量、新颖的拓扑结构与新的控制策略。直驱永磁同步风力发电机(PMSWG)没有了变速箱和励磁控制系统，而且具有更高的可靠性，其效率也比其他发电机高，逐渐成为了风力发电系统的首选[2]。

大型风电系统是复杂快变的非线性、强耦合、变量的动力学系统，具有不确定性与多干扰性的特点，并且风能具有能量密度低、随机性和不稳定性等特征。因此，先进控制策略是机组安全高效运行的保证[3]。

风电系统在额定风速下的控制目标是捕获最大风能。然而，当考虑塔影效应、风切变、风速的高频脉动分量对风电系统的影响时，传统的控制方法无法抑制系统的低频振荡，尤其是当风速中的随机脉动分量的频率不太大时，会导致系统瞬时失速。由于轴系存在摩擦损耗，当风力机输出的机械功率最大时，发电机获得的电磁功率不一定最大，此时系统的最优叶尖速比发生了偏移。

基于此，文章详细阐述了系统低频振荡产生的原因，通过引入补偿转矩有效地解决了风电系统的低频振荡与瞬时失速问题。并修正了最优的叶尖速比，进而实现电磁功率的最大化。

1 永磁同步风电系统模型

文章在忽略电机的电磁响应的动态过程情况下，建立了永磁同步风电系统的理想模型[4]。永磁同步风力发电系统的结构框图如图1所示。

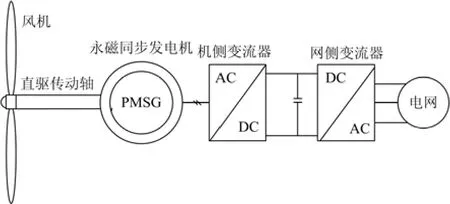
图1 永磁同步风电系统结构框图Fig. 1 Structure diagram of permanent magnet synchronous wind power system

1.1 风速模型

风速是不确定的，具有随机性与间歇性[5]。许多文献将风速v(t)看成由两个分量组成的非统计随机过程[6-7]。这里将风速看成是由低频分量与高频脉动分量的叠加，即

1.2 风力机模型

1) 基本模型

根据贝兹理论，风力机的机械功率为

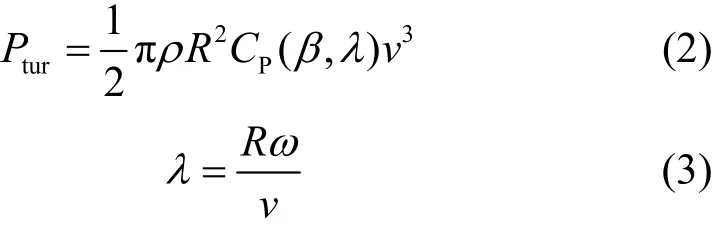
风能利用系数的表达式为

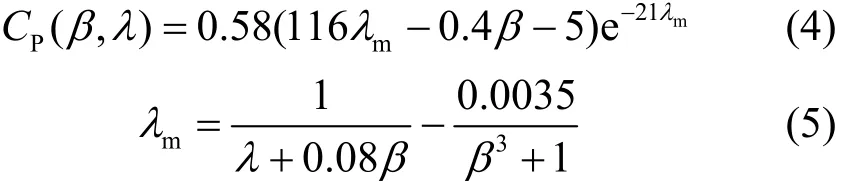
风力机输出转矩为

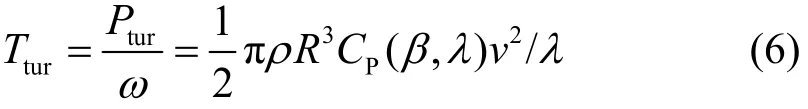
其中：ρ为空气密度；R为风轮半径；v为风速；β为桨距角；λ为叶尖速比；ω为风轮的角速度。

2) 考虑风切变和塔影效应后的风机模型

实际上，风速是随高度变化呈指数形式递增或递减的，即所谓的风的纵向剪切效应，所以，在整个风轮的回转面上风速的大小是随高度的变化而改变的，其表达式为[8]

其中：v(H)为轮廓中心高度的风速；H为轮廓中心点的高度；α为风的剪切指数。

除风切变外，塔影效应也对风力机输出的机械转矩产生影响。文献[9-12]给出了考虑风切变和塔影现象后风力机输出转矩的表达式为

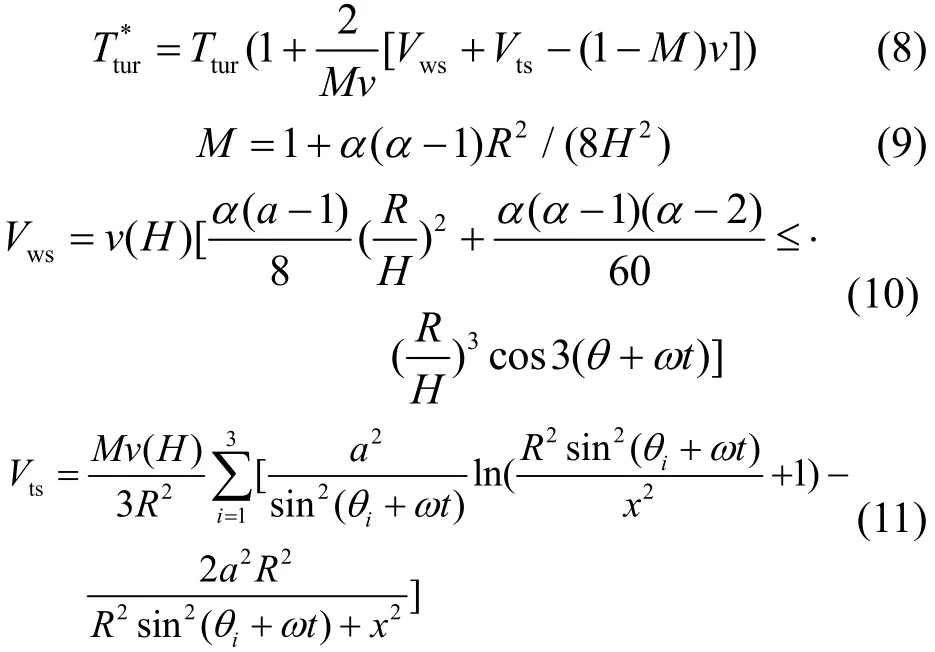
其中：Vws为考虑风切变的等效风速；Vts为考虑塔影效应的等效风速；α为塔架的半径；x为叶片回转面到塔架中线的距离；θi(i=1,2,3)为叶片的方位角；θ为其中一叶片的方位角，对于三叶片风机，相邻两个叶片之间的方位角相差120º。如图2所示，风切变和塔影现象会引起风力机输出转矩小幅波动。

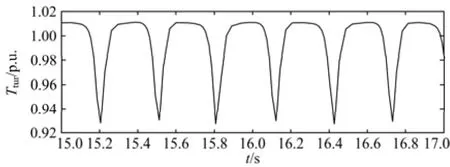
图2 风切变和塔影现象对风力机输出转矩影响Fig. 2 Influence of the tower shadow and wind shear on the wind turbine output torque

1.3 轴系模型

对于永磁同步风电系统通常是采用直驱的方式，风力机与发电机通过传动轴直接相连，一般采用如下传动模型[13]

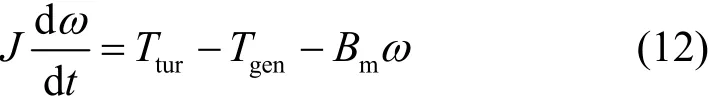
其中：J为系统的转动惯量；Tgen为电机的电磁转矩；Bm为粘滞系数。

1.4 永磁同步发电机的数学模型

假设永磁同步发电机为理想电机。满足[14]：

(1) 定子三相对称，感应电动势为正弦；

(2) 转子上没有阻尼绕组；

(3) 不考虑铁芯磁饱和、涡流及磁滞损耗；

(4) 永磁材料的电导率为0。

永磁同步电机在d-q轴下数学模型为

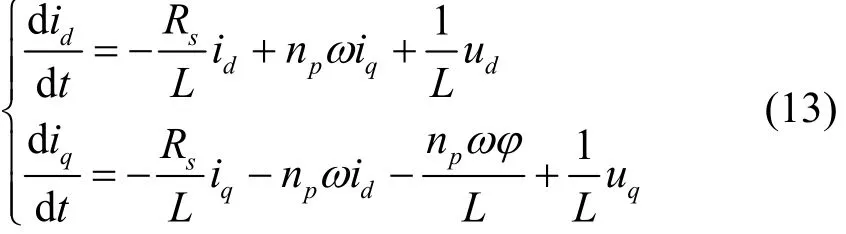
其中：L为定子电感；Rs为定子电阻；φ为永磁体磁链。

电磁转矩的表达式为

电磁功率的表达式为

2 最大风能跟踪控制

永磁同步风力发电系统在风速低于额定风速的控制目标是捕捉最大风能。其控制策略是采用转速外环控制，使风机运行在最优的叶尖速比处，实现最大风能的跟踪控制[15]。其控制框图如图3所示。

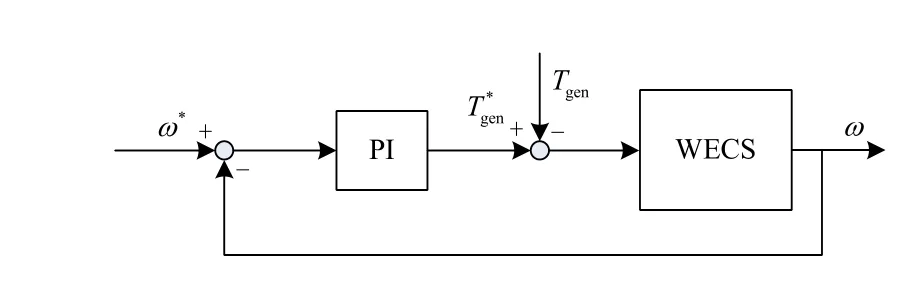
图3 转速反馈控制框图Fig. 3 Block diagram of speed feedback control

2.1 风电系统稳定性分析

当风速一定时，风力机械转矩Ttur与转速ω之间的关系如图4所示。A点为系统的平衡点，要使风力机捕获最大风能，就是让系统稳定工作在A点。

永磁同步风电系统转速外环通常采用PI控制，讨论PI控制对系统稳定性的影响。

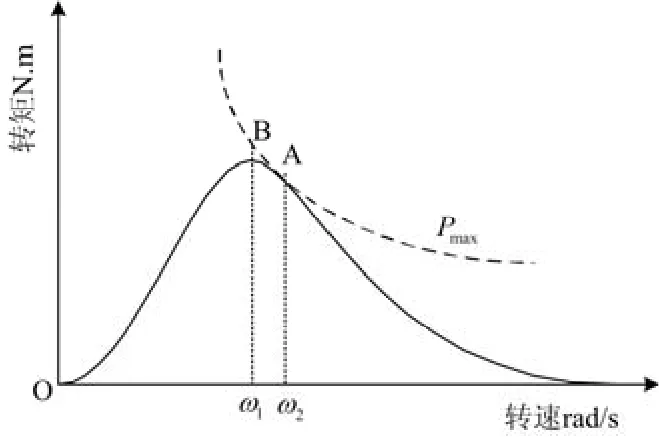
图4 风力机转矩特性Fig. 4 Torque characteristic of wind turbine

1) 当系统工作在A点时，如果存在扰动使得系统转速增大，此时，风力机的机械转矩减小，系统在PI控制下会使得系统的电磁转矩增大。这样系统转速将减小，使得系统能够重新回到A点。

2) 当系统工作在A点时，存在扰动使得系统转速减小。

3) 当系统转速从0上升到ω0时，由于e=ω-此时系统的电磁转矩与转速同方向，系统处在电动状态，，电磁转矩才能逐渐跟上机械转矩，故转速超调不可避免。

所以，选择合适的PI参数是系统稳定运行的关键，好的一组PI参数能使系统保持大范围稳定。但是，由于永磁同步风力发电系统是一个复杂多变的非线性、强耦合系统，其PI参数的整定具有一定的盲目性。

2.2 风电系统低频振荡分析

当考虑到塔影、风切变、风湍变与高频脉动时，在追求捕获最大风能这一单一控制目标下，传统的转矩控制方法会引起系统转速的大范围波动。转速波动又会影响叶尖速比λ与风能利用系数CP变化，加剧风力机的机械转矩Ttur波动，进而使系统发生低频振荡。所以，在一定程度上，减小转速波动有利于抑制风电系统的低频振荡。

由传动轴系模型公式(12)可知，风力机的转速波动主要是由于风力机输出转矩波动与电机的电磁转矩波动共同引起的。转速动态可表示为

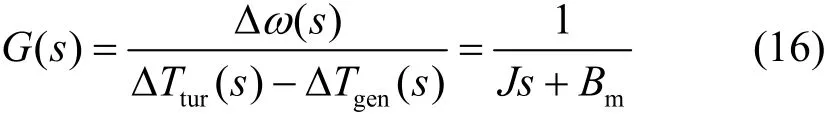
由公式(16)可知，转速波动可看做是转矩波动进行一次惯性滤波。随着风机容量增大，风机输出转矩的波动不断增大。当系统的转动惯量J一定时，由于系统的阻尼不足，削弱了G(s)的滤波能力，最终加大了转速波动。

实际上，系统的电磁转矩是可控的。如果能控制电磁转矩实时地跟踪上风机的机械转矩，就可以大大地减小转速波动，进而抑制系统的低频震荡。这样需要对风力机的机械转矩波动进行估计或测量，就要简化风速模型或增加控制成本。

2.3 风电系统电磁转矩控制

文章在电磁转矩控制中引入转速补偿转矩，其控制框图如图5所示。

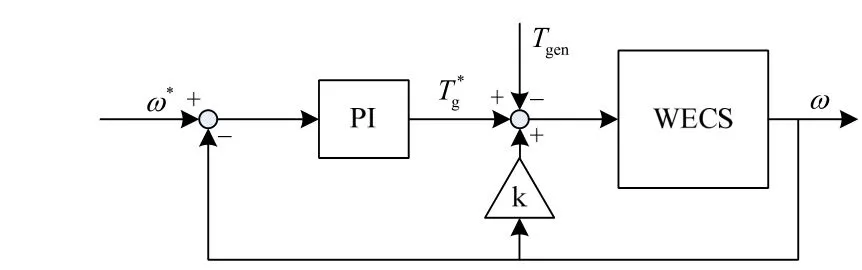
图5 转速补偿后的转矩控制框图Fig. 5 Block diagram of speed compensation torque control

据图5，有

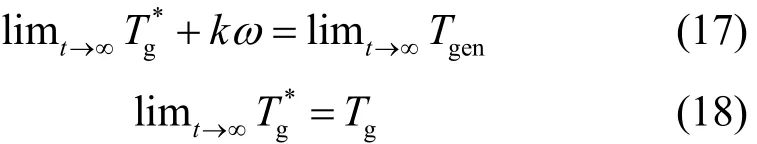
由于系统的电气部分的响应速度远远高于机械部分的响应速度[16]。此时电磁转矩可以看作是两部分的叠加。据式(17)、式(18)可以得出：

此时，转速的动态表示为

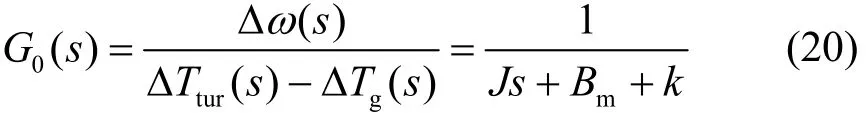
这样，增大k就能减小其静态增益，提高G0(s)的滤波能力，削弱转矩波动对转速的影响。但是，由于静态增益的减小可能会延长转速的上升时间。

若转速外环采用PI控制，即

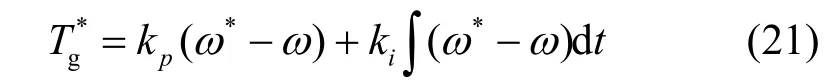
那么，可以将图5转换成图6。很显然，此时的控制目标可以看作是包含以下两个控制目标按一定权值叠加的综合控制。

控制目标1：系统转速渐进跟踪给定转速，即

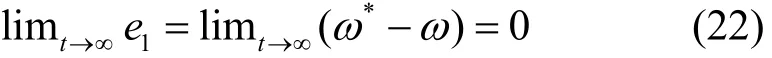
控制目标2：系统转速的变化不能太快，取给定值为0来镇定转速的变化率，即

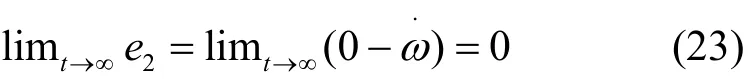
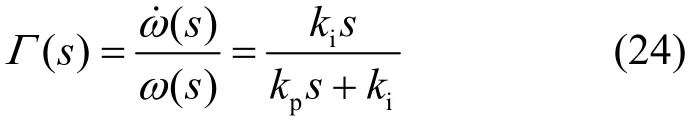
所以，k值的增大也就相当于增大了目标2的权值，也同样解释了k会对转速波动与转速的上升时间产生影响。

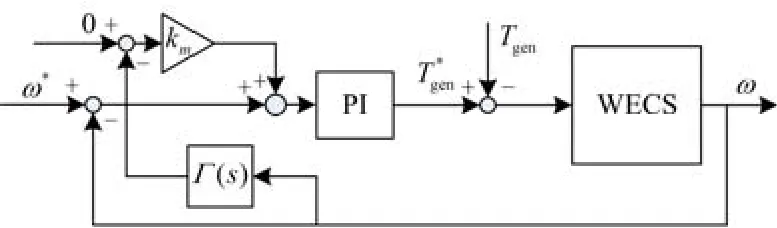
图6 等效的双目标综合控制框图Fig. 6 Block diagram of equivalent double objective comprehensive control

k的大小影响系统转速的上升时间，这对系统而言是不利的，所以需要对k进行优化，进一步提升系统性能。控制工程界长期以来一直有一个经验的认识：“大误差，小增益；小误差，大增益”。变增益PID控制，模糊控制，更加智能的控制，都是基于这个经验认识[17]。所以，k与误差e1应满足：

(1) 当误差e1较大时，希望k取较小的值，减小对转速上升时间的影响。

(2) 当误差e1较小时，希望k取较大的值，抑制转速波动。

文章采用模糊的方法对k进行优化，如图7所示。具体步骤如下：

Step 1 对e1与k进行量化。

Step 2 确定e1与k的隶属度函数。

Step 3 制定模糊规则表。

Step 4 根据规则，推理并计算k值。

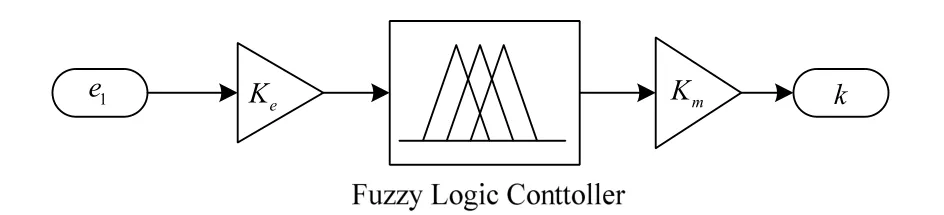
图7 模糊逻辑框图Fig. 7 Fuzzy logic diagram

误差e1的变化范围为[-emax，emax]，emax= λopt·vmax/R；k的变化范围为[0,kmax],kmax为设定值，一般取较大的值；量化因子Ke=n/emax，Km=kmax/m，取n=m=6；e1的模糊论域为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6 }，k的模糊论域为{0，1，2，3，4，5，6}；表1给出了模糊规则。

表1 模糊规则表Table 1 Fuzzy rule

2.4 获取最大的电磁功率

由于轴系存在阻尼损耗，当风力机输出的机械功率最大时，发电机吸收的电磁功率不一定最大。所以，当考虑到损耗时，系统最优的叶尖速比可能发生偏移，以此计算的给定转速也是不准确的。

当转速稳定时(即：dω/dt=0)，由公式(12)得

风速一定时，据式(2)、式(3)、式(25)可知

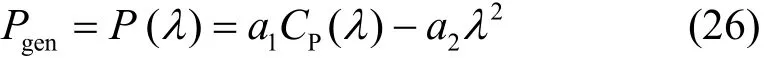
其中：a1=0.5πρR2ν3；a2=Bmν2/R2。

求取λ*，使得max(Pgen)。

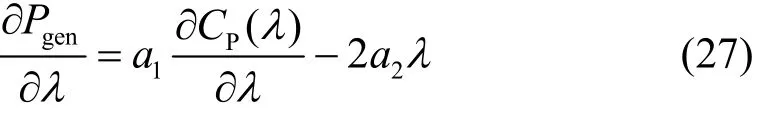
图8表示了曲线c与直线l之间的位置关系(f为λ的函数)。一般情况下，c与l有3个交点，分别为λ1、λ2和0。否则λ*=0，与事实不符。

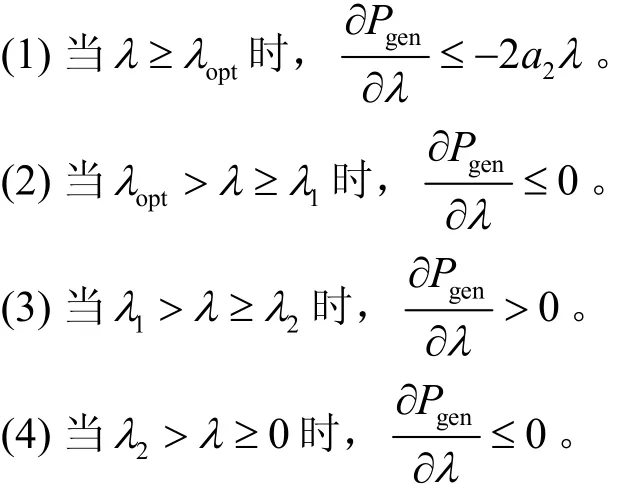
所以，λ*=λ1<λopt。λopt→max(Ptur)或max(CP(λ))。

实际情况下，a1>>2a2，这就导致λ*相对于λopt偏移量很小,且P(λopt)>P(λ2)。因此，可以从λopt处开始搜索。

一维搜索只能针对单峰函数，但是本例中存在两个峰值，分别对应λ1和λ2。所以在采用Fibonacci法[18]搜索之前，必须要先准确地确定其大致的搜索范围。可由λopt处慢慢地减小λ，直到P(λopt)- P(λ)>0，搜索步长λf应该满足λf< λopt- λ2。

主要步骤如下：

Step 1 根据风速ν计算参数ɑ1和ɑ2。

Step 2 设置初值、误差精度e0与搜索步长λf。

Step 3 粗略判断搜索的范围。

Step 4 采用Fibonacci法进行精确搜索。

Step 5 离线的得出λ*与Bm、ν之间的关系。

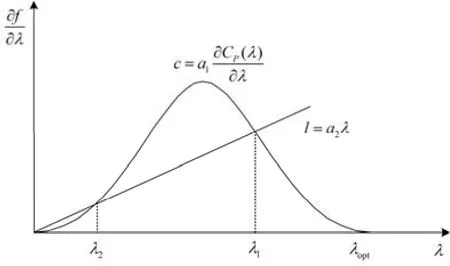
图8 曲线c与lFig. 8 Curve and linear

图9 给出了风速ν在[1,14]变化时，Bm在[0,130]时，λ*与Bm、ν之间的关系。虽然λ*为Bm与ν的二元函数，但是一般情况下，系统的粘滞摩擦系数Bm为系统参数，所以当系统唯一确定时，Bm一般取固定的值。

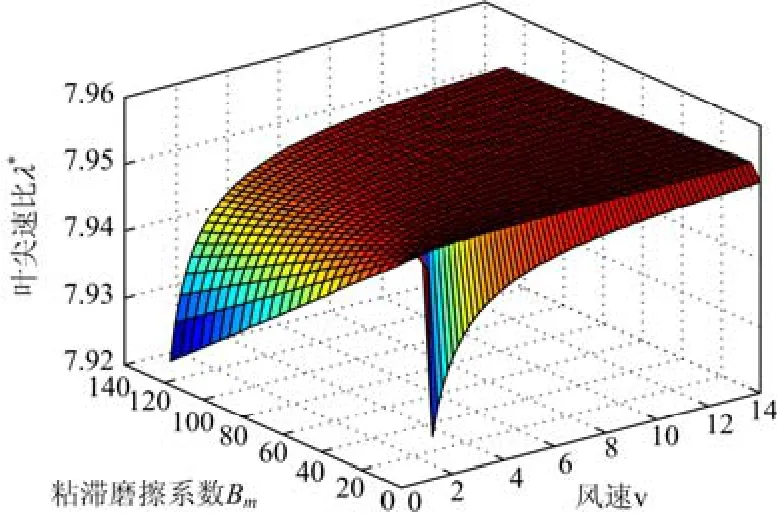
图9 λ*与Bm、ν之间的关系Fig. 9 Relationship between λ*and Bm, ν

当Bm一定时，λ*只取决于ν。在Matlab下调用cftool工具箱对所得数据进行拟合，得到λ*与ν之间的关系式。文章中取Bm=10，在cftool工具箱采用9阶多项式拟合，如图10所示。由图10可知风速在[0,14]变化时，该拟合比较有效，各项指拟合标优异，能正确反映λ*与ν之间的关系。

求得多项式系数如下：

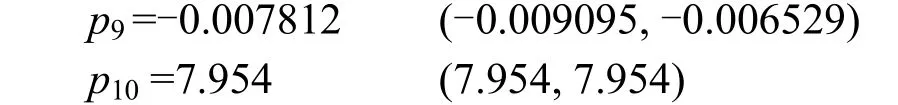
拟合优度：

残差平方和SSE: 3.79e-08

确定性系数(相关系数)的平方 R-square: 0.9933

可调确定性系数的平方Adjusted R-square: 0.9833

均方差RMSE: 7.948e-05

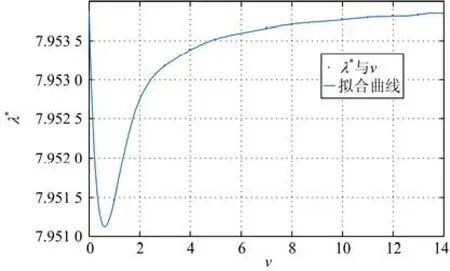
图10 λ*与ν之间的拟合关系Fig. 10 Fitting relationship between λ*and ν

以上求出了3组多项式的拟合系数，这3组系数是完全等价的，任选一组带入式(28)，就可以得到λ*较为准确的表达式。

所以，通过多项式拟合，λ*可以近似表达为

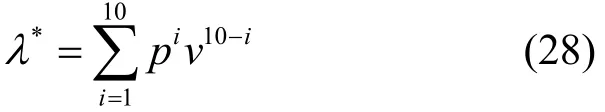
3 仿真分析

文章在Matlab/Simulink下构建永磁同步风电系统的仿真模型，进行理论验证。风电系统的仿真参数如表2所示。

当考虑塔影与风切变的影响时，如图11所示,改进型控制方式相对于传统的控制方式明显减小了系统转速波动与风能利用系数CP的波动。

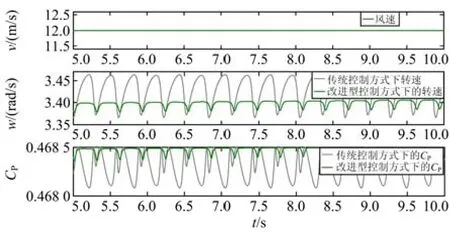
图11 塔影与风切变对系统的影响程度Fig. 11 Influence of the tower shadow and wind shear on the system

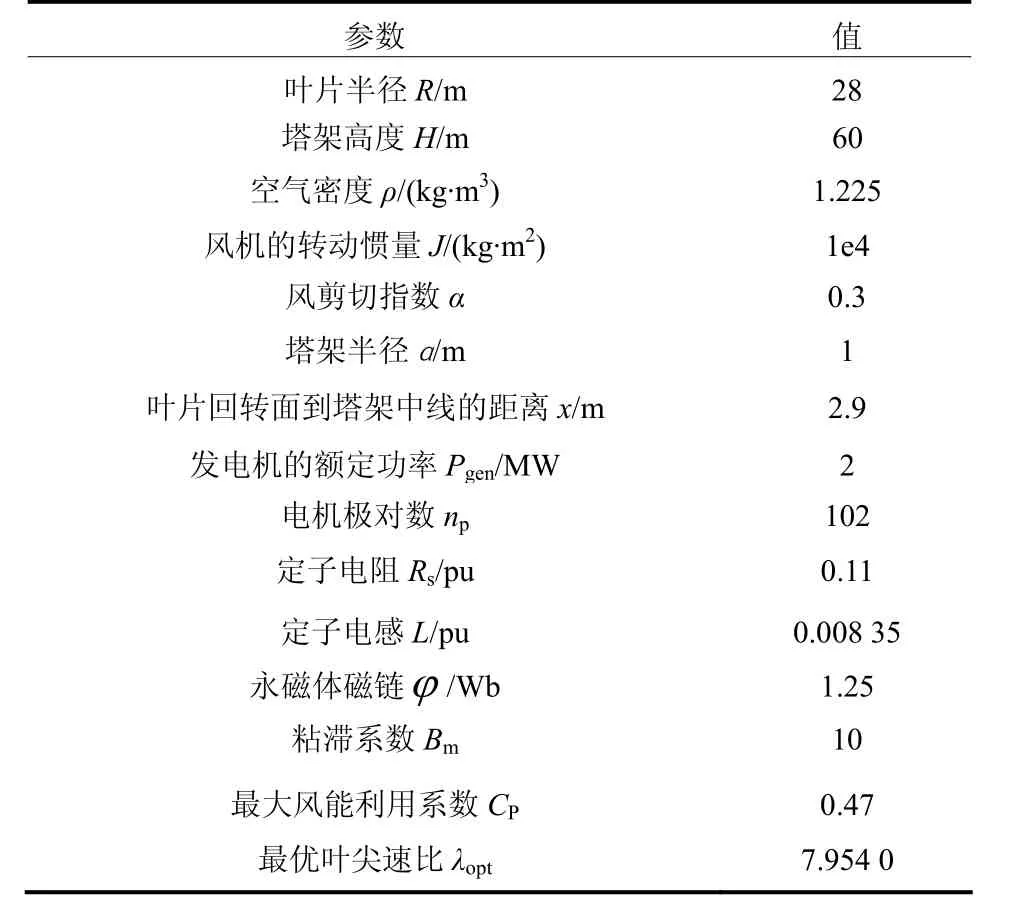
表2 风力发电系统参数Table.2 Wind power system parameters

由于轴系损耗与转速有关，会使系统最优叶尖速比发生偏移，导致按照最优叶尖速比法计算的给定转速(ω*=λopt×v/R)不准确。使得系统没有工作在最大电磁功率对应的工作点处。文章通过计算最优叶尖速比，得出了准确的ω*，使得电磁功率最大化。当考虑轴系的摩擦损耗时，修正后的最优叶尖速比明显提升了系统的电磁功率，其仿真结果如图12所示。

图12 修正前后的最优叶尖速比对系统的影响Fig. 12 Influence of the optimal tip speed ratio on the system

综合考虑风速脉动、塔影与风切变、轴系摩擦损耗对系统的影响，其仿真结果如图13所示。仿真中用慢时变的信号来模拟风速的低频分量用快速变化的随机信号来模拟风速中所含有的高频脉动分量∆ν(t)(-1<∆ν<1)。

通过仿真对比得出：

1) 当风速中含有的随机脉动信号变化不是很快时，采用传统的控制方法，会导致系统失速。伴随着转速跌落的同时系统的电磁功率Pgen、风能利用系数CP都发生了跌落。

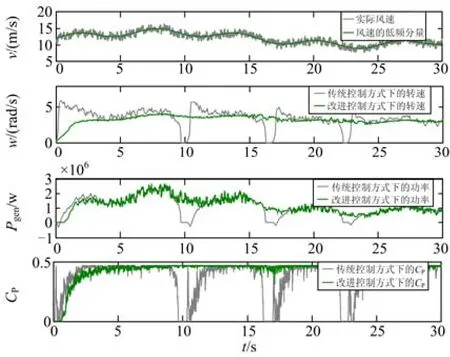
图13 仿真结果Fig. 13 Simulation diagram of results

2) 在考虑了塔影效应、风切变、风湍变与风速中所含高频脉动分量对系统的影响时，传统的控制方法无法抑制系统的低频振荡。

3) 通过引入补偿转矩控制，减小系统低频振荡的同时也防止了转速、电磁功率Pgen、风能利用系数CP的瞬时跌落。

4) 通过修正最优的叶尖速比，得出了准确的ω*，使得电磁功率Pgen也有了小幅的提升。

4 结论

该文通过在电磁转矩控制中加入补偿转矩，增强了系统针对转速波动的阻尼，抑制了系统的低频振荡，增强了系统的稳定性，显著改善了系统的性能，并考虑了轴系的粘滞摩擦损耗，得出了最优叶尖速比的计算公式，真正实现了最大风能跟踪，通过仿真对比验证了其有效性。

[1] World Wind Energy Association. World wind energy report 2009[R]. 2009.

[2] YAN Jianhu, LIN Heyun, FENG Yi, et al. Improved sliding mode model reference adaptive system speed observer for fuzzy control of direct-drive permanent magnet synchronous generator wind power generation system[J]. IET Renewable Power Generation, 2013, 7(1): 28-35.

[3] 崔双喜, 王维庆, 张强. 风力发电机组独立变桨鲁棒自适应桨距角跟踪控制[J]. 电力系统保护与控制, 2015, 43(6): 52-57. CUI Shuangxi, WANG Qingwei, ZHANG Qiang. The independent robust adaptive pitch Angle tracking control in wind turbine[J]. Power System Protection and Control, 2015, 43(6): 52-57.

[4] 管维亚, 吴峰, 鞠平. 直驱永磁风力发电系统仿真与优化控制[J]. 电力系统保护与控制, 2014, 42(9): 54-60. GUAN Weiya, WU Feng, JU Ping. The simulation and optimization control in direct-drive permanent magnet wind power system[J]. Power System Protection and Control, 2014, 42(9): 54-60.

[5] 张涛, 胡立锦, 张新燕, 等. 风力发电机通用化建模研究[J]. 电力系统保护与控制, 2013, 41(13): 1-6. ZHANG Tao, HU Lijin, ZHANG Xinyan, et al. The generalized modeling research of wind turbine[J]. Power System Protection and Control, 2013, 41(13): 1-6.

[6] BIANCHI F D, DE BATTISTA H, MANTZ R J. Wind turbine control systems: principles, modelling and gain scheduling design[M]. Springer Science & Business Media, 2006.

[7] NICHITA C, LUCA D, DAKYO B, et al. Large band simulation of the wind speed for real time wind turbine simulators[J]. IEEE Transactions on Energy Conversion, 2002, 17(4): 523-529.

[8] THIRINGER T, DAHLBERG J Å. Periodic pulsations from a three-bladed wind turbine[J]. IEEE Transactions on Energy Conversion, 2001, 16(2): 128-133.

[9] HUANG Huazhang, CHUNG Chiyung. Adaptive neurofuzzy controller for static VAR compensator to damp out wind energy conversion system oscillation[J]. IET Generation, Transmission & Distribution, 2013, 7(2): 200-207.

[10] DOLAN D S L, LEHN P W. Simulation model of wind turbine 3p torque oscillations due to wind shear and tower shadow[C] // Power Systems Conference and Exposition, 2006. PSCE'06. 2006 IEEE PES. IEEE, 2006: 2050-2057.

[11] DE KOONING J D M, VANDOORN T L, VAN DE VYVER J, et al. Shaft speed ripples in wind turbines caused by tower shadow and wind shear[J]. IET Renewable Power Generation, 2014, 8(2): 195-202.

[12] WANG Biao, DING Lijie, ZHANG Hua, et al. Study of the directly type driven of permanent magnet synchronouswind turbine containing the dynamic characteristics[C] // Power and Energy Engineering Conference (APPEEC) 2012 Asia-Pacific: IEEE, 2012: 1-4.

[13] LI S, HASKEW T A, SWATLOSKI R P, et al. Optimal and direct-current vector control of direct-driven PMSG wind turbines[J]. IEEE Transactions on Power Electronics, 2012, 27(5): 2325-2337.

[14] SHEN Yanxia, LI Fan, WU Dinghui, et al. Space based direct-driven permanent magnet synchronous wind power system modeling and simulation[C] // Control (CONTROL), 2012 UKACC International Conference on: IEEE, 2012: 809-812.

[15] 李咸善, 徐浩, 杜于龙. 采用叶尖速比法和爬山搜索法相结合的风力发电系统最大功率点跟踪研究[J]. 电力系统保护与控制, 2015, 43(13): 66-71. LI Xianshan, XU Hao, DU Yulong. Maximum power point tracking of wind power generation system using the combination of tip speed ratio method and climbing search method[J]. Power System Protection and Control, 2015, 43(13): 66-71.

[16] GENG Hua, XU Dewei. Stability analysis and improvements for variable-speed multiple permanent magnet synchronous generator-based wind energy conversion system[J]. IEEE Transactions on Sustainable Energy, 2011, 2(4): 459-467.

[17] HAN Jingqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2008, 56(3): 900-906.

[18] 陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社有限公司, 2005.

(编辑 葛艳娜)

Research of maximum wind power tracking control strategy of permanent magnet synchronous wind power system based on the tower shadow and wind shear

LIU Jun1, ZHOU Feihang1, LIU Fei1,2
(1. College of Automation, Xi’an University of Technology, Xi’an 710048, China; 2. Armed Police Engineering University, Xi’an 710048, China)

In order to ensure the high-efficiency and stable operation of the wind turbines, this paper presents compensation torque of fuzzy variable gain in torque control. The influence of mechanical torque fluctuation of wind turbines caused by random dither component of the tower shadow effect, wind shear, wind speed and reference rotation fluctuation calculated via optimal tip speed ratio on permanent magnet synchronous wind power system is alleviated effectively, the low frequency oscillation of wind power system is suppressed, and the stability of the system is ensured. It calculates accurate reference speed of maximum electromagnetic power by modifying the optimal tip speed ratio, and makes the unit run at the corresponding working point of maximum electromagnetic power. It truly achieves the maximum wind power tracking, by calculating the optimal tip speed ratio, considering the shafting friction loss. A direct-driven permanent magnet synchronous wind power system simulation platform is built in detail under Matlab/Simulink, and the correctness and effectiveness of the method is proved.

tower shadow effect; wind shear; permanent magnet synchronous wind power system; low frequency oscillation; tip speed ratio

10.7667/PSPC150926

2015-06-03；

2015-07-20

刘 军(1963-)，男，教授，博士生导师，研究方向为风力发电系统控制策略，无线电能传输，高压自取电装置，电力系统自动化，智能控制，电机与电器等;

周飞航(1989-)，男，通信作者，硕士研究生，研究方向为永磁同步风力发电系统控制策略的研究；E-mail：qq987102679@126.com

刘 飞(1982-)，男，博士研究生，研究方向为风力发电系统载荷优化控制。