扬线段图形之帆启应用模型之航

徐玉宇

扬线段图形之帆启应用模型之航

徐玉宇

课标提出：结合具体的教学内容采用“问题情境—建立模型—解释、应用与拓展”的过程来进行教学，让学生经历数学建模的全过程，提高数学的应用意识和应用数学知识解决实际问题的能力。由此可见，数学应用首先要建立数学模型，将纷繁的现实情境用简约的数学语言表示出来，表示能力是培养应用能力的关键之一。在这里，线段图即为简约的数学语言，它能把纷繁复杂的文字转化成简单易懂的图形，借助线段图，可以使学生进行形象的思考、有条理的分析，更加容易建立基本应用模型。

一、借助线段图析关系

解决问题的数量关系各式各样，如果要记住类型纷繁复杂的数量关系，容易造成学生解决问题时，套用公式，不利于学生灵活性思维的培养。而有了线段图这样的工具，能将复杂抽象的问题，借助线段图理解、分析数量关系，不至于简单机械地利用数量关系解决问题。只有在理解的基础上，分析数量关系，学生才会明白解决问题的真谛，同时经常利用线段图解决问题，学生遇到复杂的问题时，自然而然就借助线段图帮助解决问题。

例如：四年级下册第一单元中有这样的问题：书架上有两层书，共144本。如果从下层取出8本放到上层去，两层书的本数就相同。书架上、下层各有多少本书？

对于这样的问题，很多学生束手无策，如果借助线段图分析数量关系，绝大多数学生都能解决这道问题。

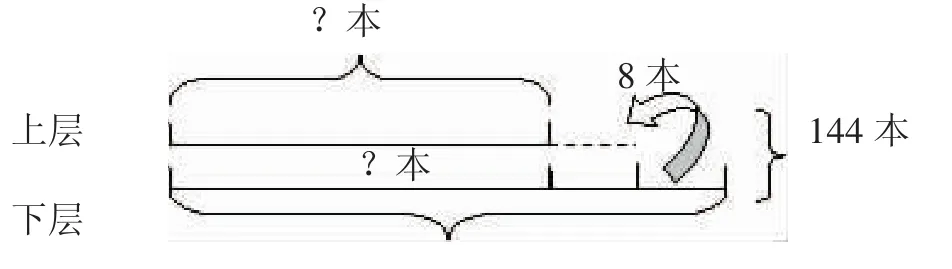
借助线段图分析，学生可以列出先求上层（144-8×2）÷2= 64（本），再求下层144-64=80（本）；也可以列出先求下层（144+8×2）÷2=80（本），再求上层144-80=64（本）；还可以列出先求两层同样多的本数：144÷2=72（本），再求下层72+8= 80（本），那么72-8=64（本）为上层。结合线段图不难理解各种数量之间的关系，又有利于拓展学生的思维。

如果经常应用线段图分析类似问题的数量关系，可以为学生在脑中构建基本应用模型奠定基础，有了这种依托，在构建某种模型时，教师稍作引导，学生更容易将这类复杂的问题在脑中形成基本的应用模型，以后遇到相似的问题，就可以运用这种基本应用模型解决问题。

二、借助线段图明结构

解决问题不再按类型教学后，学生对“解决问题”的基本结构也很模糊。明确“解决问题”的结构，有助于学生建构基本应用模型，也更有利于学生更好地解决问题。线段图就是一种很好的媒介，借助它可以明确“解决问题”的基本结构，也更易于学生洞察结构之间的变化，根据变化就可以对解题方案作出适当调整，从而更顺利解决问题。

例如：像行程问题中的相遇问题就有很多类型。

（1）甲乙两车从A、B两地相向而行，甲车的速度为每小时80千米，乙车的速度为每小时70千米，3小时后两车相遇。A、B两地相距多少千米？

（2）甲乙两车从某地出发，相背而行，甲车的速度为每小时80千米，乙车的速度为每小时70千米，3小时后两车相距多少千米？

（3）甲乙两车从某地出发，同向而行，甲车的速度为每小时80千米，乙车的速度为每小时70千米，3小时后两车相距多少千米？

（4）甲乙两车从A、B两地相向而行，甲车的速度为每小时80千米，乙车的速度为每小时70千米，3小时后两车还相差100千米才相遇。A、B两地相距多少千米？

（5）甲乙两车从A、B两地相向而行，甲车的速度为每小时80千米，乙车的速度为每小时70千米，行了3小时，两车相遇之后相差100千米。A、B两地相距多少千米？

……

借助线段图，学生不需要记忆这么多的“相遇问题”，只要画出线段图，就可以明确变化多端的相遇问题的结构，借助线段图解决这些问题。

有了线段图的介入，对于其他变换多端的“解决问题”的结构，学生也不用机械记忆了，只要借助线段图，就可以明确它们的结构，多次熟悉这些结构之后，学生会形成自己对基本结构的认识，有利于基本应用模型的建立，也更有助于解决问题。

三、借助线段图建模型

学生要解决内容和形式各式各样的问题，可对一些基本和常态的问题建立模型，依照模型解决问题，更有益于学生判断和分析基于基本应用模型之上的各式各样的“解决问题”。借助线段图，可以将各种类型的“解决问题”进行沟通，建立基本的模型。

例如：

方方有12本故事书，8本科技书。她共有几本书？

方方原有12本故事书，又买来8本。她共有几本书？

方方共有20本书，其中12本故事书。她有几本科技书？

方方共有20本书，捐了12本，还剩几本书？

方方共有20本书，捐了一些后，还剩12本书，她捐了几本？

当用线段图表示这些问题时，可以发现都能用这样的线段图表示这些原型“解决问题”：

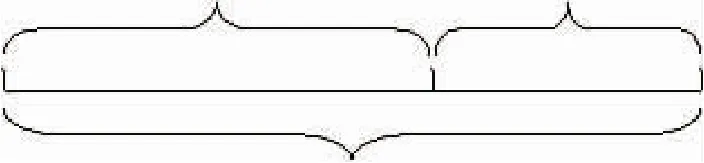
又可以从线段图中，清楚地将这些数量关系的问题归结为两类，求总数和求部分数，使学生能将各种纷繁复杂的数量关系归成两类基本模型，抓住了问题的本质，有利于学生解决好问题。

在建构的这两类基本模型之上，可以对基本模型进行适当的拓展，拓展到分数、小数的“解决问题”；也可以通过条件的间接化，对“解决问题”进行拓展，拓展到多步的“解决问题”。

例如对“方方有12本故事书，8本科技书。她共有几本书？”拓展到：“方方有8本科技书，她又买了3次故事书，每次买了4本。她共有几本书？”借助下面的线段图分析：

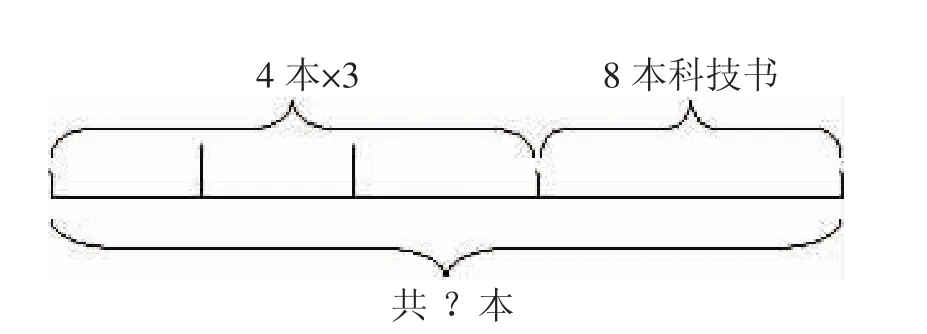
可以知道求共有几本书，就是把故事书与科技书合并，而故事书没有直接说几本，那么首先要求出故事书的本数，基本模型还是把两个部分数进行合并。对于这样的求总数的基本模型，还可以进行其他的拓展，借助线段图，可以将各类“解决问题”收于基本模型之下。对于其他的基本应用模型也可以借鉴求总数，求部分的解决问题方式进行建构。

虽然教材中线段图出现的次数并不多，但作为一线教师却要重视和加强线段图辅助解决问题的有关教学。在教学过程中，要注意循序渐进，适当运用，把线段图作为一种解决问题的辅助策略教学，作为学生解决问题的基本能力来培养，真正扬起线段图之帆，启应用模型之航，使线段图真正成为学生解决问题的好助手。

（作者单位：浙江省玉环县古顺学校 317604）

责任编辑：金锡萍