例谈初中数学教学中的思维能力培养

叶超荣

例谈初中数学教学中的思维能力培养

叶超荣

在教育教学过程中培养学生的良好思维品质是非常重要的，教学实践过程中，深深感到数学课能起到培养学生思维品质的作用。思维是人脑对客观事物的一种间接的、概括的反应过程，培养学生的思维能力是使学生获取知识进行创新学习和发展智力的重要途径。素质教育的核心就是要培养学生的创新精神和创新能力，这两点都要求具有良好的思维品质，因此在数学教学中，应充分注意和提高学生的思维能力。在进行数学教学过程中，我尝试从以下几方面来培养和提高学生的思维能力。

一、质疑思维的培养

古希腊哲学家亚里士多德认为“思维从惊奇和质疑开始”。因而教师在教学中，应根据数学问题本身所特有的丰富内涵，巧妙地创设情境、诱发疑问，使矛盾、问题不断产生，以保持和强化学生的好奇心和想象力。例1：过△ABC顶点C任作一直线，与边AB及中线AD分别交于点F及E。求证：AE：ED=2AF：FB。本题证题途径极为广阔，教师在讲完一种证法后,依次提出如下问题：（1）本题有十多种证法，大家试试能用几种方法证明。（2）由题设知F是AB上（或AB延长线上）任一点，那么其结论总能成立，这是为什么？（3）若D分 BC成等，其他条件不变，其结论如何？你发现了什么规律？

这样逐步把问题引向深入，给原较为枯燥的命题增添了神奇感，使其有了浓厚的趣味性，创设质疑和认识冲突的情境，促使学生求知欲进入活跃状态。

二、转移思维的培养

转移思维是数学中一种重要的思维方法——“化归”思想的集中体现。转移思维就是注意开阔自己的视野，不使思维定于某一点或某个侧面，而注意矛盾和问题的转化，把复杂、生疏的问题转化为比较简单、熟悉的问题。

例2：已知a≥2解关于X的方程X4－4X3＋4X2－2aX2＋a2－9=0

此方程是一个关于未知数X的四次方程，此方程是学生所不熟悉的，用常规方法解比较困难，现考虑将已知与未知做一转化，即把未知数X当作已知量，把常数a当作未知量，问题就可迎刃而解了。

解：把原方程化为关于a的方程：

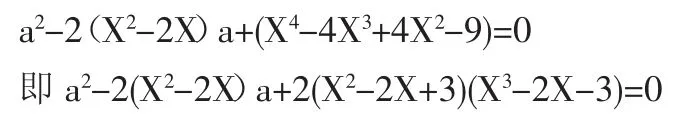
三、发散思维的培养

发散思维即是从一点向四周横辐射的一种思维方式。发散思维有“三个维度”，即思维流畅度、思维变通度和思维独创度。根据这个理论，教师在教学中应注重培养学生从不同的角度，运用不同的方法，全方位分析和探索问题的能力。

例3：已知抛物线经过两点A（1、0），B（3、C）且顶点是C（2、1），求函数的解析式？

方法一：若用一般式，可设所求的解析式为y=ax2＋bx＋c

∴所求函数的解析式为y=－x2＋4x－3

方法二：若用顶点式，可设二次函数的解析式为y=a(x－2)2＋1

∵抛物线经过A（1，0），代入上式，得a(x－2)2＋1=0解方程得a=－1

∴所求的函数的解析式为：－(x－2)2＋1

即y=－x2＋4x－3

方法三：若用双根式，可设函数的解析式为：y＝a（x－x1)(xx2)，其中x1，x2是抛物线与x轴的交点横坐标。

∵抛物线与x轴的交点为A（1，0），B（3，0）

∴y＝a（x－1)(x－3)

抛物线经过C（2，1）

∴a=－1

∴所求的二次函数的解析式为：y＝－（x－1)(x－3)

即y=－x2＋4x－3

四、逆向思维的培养

在解题过程中，若正面解题有困难或无法舒展思维，则转向逆面或倒过来思考这就是逆向思维，即打破习惯的思考方法，去做与习惯的思考方向相反的探索。这种思维方式通常是由果寻因。它对一些较为抽象的问题往往容易找到解题的途径。

例4：已知三个方程x2＋4ax＋3－4a=0，x2＋(a－1)x＋a2=0，x2＋ 2ax－2a=0中至少有一个方程有实数根，求实数a的取值范围。分析：本题若从正面考虑，则很难求出a的取值范围。而本题如果从反面考虑，方程全无实数根，则易解决，由△1＜0，△2＜0，△3＜0，故本题a的取值范围是a≤－3

2或者说a≥－1。

因此，在教学中，通过引导学生正面解题难则以反向思维方式去思考解答问题，常常收到事半功倍的解题效果。

五、思维敏捷性的培养

在考试中学生解题既要讲究准确，又要讲究速度。要提高学生应变能力，提高解题速度，就必须培养学生思维的敏捷性，在教学中就要多进行一题多变的练习。

例5：如图已知⊙O的弦AB的延长线和切线EP相交于点P，E为切点，∠APE的平分线和AE，BE分别相交于C、D，求证：CE=ED

证明：略

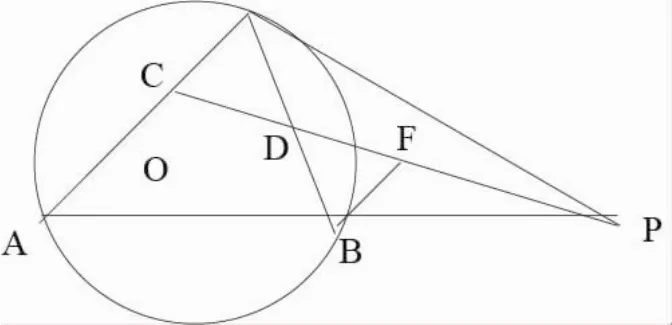
本题在题设条件不变的情况下，变换其结论，可得下列系列变式题，求证：

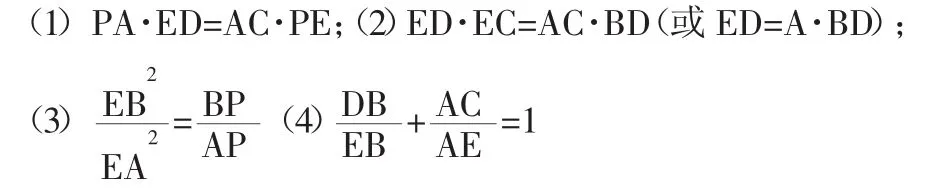
本题若保持图形不变，适当变换条件和结论，又可得到下列一组题：

（1）⊙O的弦AB的延长线和切线EP相交于点P，E为切点，点C为AE的中点，PC交BE于点D，求证：

（2）⊙O的弦AB的延长线和切线EP相交于点P，E为切点，过点P的直线分别交AE、BE于C、D，若EC=ED，求证：∠APC=∠CPE。

通过对同一道题条件和结论的变换，灵活应用所学知识，达到融会贯通的目的，拓展了思路，无疑对提高分析和解决问题的能力有极大的帮助，从而培养学生思维的敏捷性。

（作者单位：江西省龙南县临塘学校 341708）

责任编辑：乔 健